 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Degradelere giriş ve otomatik farklılaşma kılavuzu, TensorFlow'da degradeleri hesaplamak için gereken her şeyi içerir. Bu kılavuz, tf.GradientTape API'sinin daha derin, daha az yaygın özelliklerine odaklanır.
Kurmak
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
Gradyan kaydını kontrol etme
Otomatik farklılaşma kılavuzunda , gradyan hesaplamasını oluştururken bant tarafından hangi değişkenlerin ve tensörlerin izlendiğini nasıl kontrol edeceğinizi gördünüz.
Kaset ayrıca kaydı manipüle etme yöntemlerine de sahiptir.
Kaydetmeyi bırak
Degradeleri kaydetmeyi durdurmak isterseniz, kaydı geçici olarak askıya almak için tf.GradientTape.stop_recording kullanabilirsiniz.
Bu, modelinizin ortasında karmaşık bir işlemi ayırt etmek istemiyorsanız, ek yükü azaltmak için yararlı olabilir. Bu, bir metrik veya bir ara sonucun hesaplanmasını içerebilir:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Sıfırla/kaydı sıfırdan başlat
Tamamen baştan başlamak istiyorsanız, tf.GradientTape.reset kullanın. Degrade bant bloğundan çıkmak ve yeniden başlatmak genellikle daha kolaydır, ancak bant bloğundan çıkmak zor veya imkansız olduğunda reset yöntemini kullanabilirsiniz.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Gradyan akışını hassas bir şekilde durdurun
Yukarıdaki genel teyp kontrollerinin aksine, tf.stop_gradient işlevi çok daha kesindir. Bantın kendisine erişmeye gerek kalmadan belirli bir yol boyunca gradyanların akmasını durdurmak için kullanılabilir:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Özel degradeler
Bazı durumlarda, varsayılanı kullanmak yerine degradelerin tam olarak nasıl hesaplandığını kontrol etmek isteyebilirsiniz. Bu durumlar şunları içerir:
- Yazmakta olduğunuz yeni bir operasyon için tanımlanmış bir gradyan yok.
- Varsayılan hesaplamalar sayısal olarak kararsızdır.
- İleri geçişten pahalı bir hesaplamayı önbelleğe almak istiyorsunuz.
- Bir değeri (örneğin,
tf.clip_by_valueveyatf.math.roundkullanarak) degradeyi değiştirmeden değiştirmek istiyorsunuz.
İlk durumda, yeni bir operasyon yazmak için tf.RegisterGradient kullanarak kendinizinkini oluşturabilirsiniz (ayrıntılar için API belgelerine bakın). (Degrade kayıt defterinin genel olduğunu unutmayın, bu nedenle dikkatli bir şekilde değiştirin.)
Son üç durum için tf.custom_gradient kullanabilirsiniz.
Ara gradyana tf.clip_by_norm uygulayan bir örnek:
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
Daha fazla ayrıntı için tf.custom_gradient dekoratör API belgelerine bakın.
SavedModel'de özel degradeler
Özel degradeler, tf.saved_model.SaveOptions(experimental_custom_gradients=True) seçeneği kullanılarak SavedModel'e kaydedilebilir.
SavedModel'e kaydedilebilmesi için, gradyan işlevi izlenebilir olmalıdır (daha fazla bilgi için, tf ile daha iyi performans kılavuzuna bakın).
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Assets written to: saved_model/assets tf.Tensor(2.0, shape=(), dtype=float32)
Yukarıdaki örnekle ilgili bir not: Yukarıdaki kodu tf.saved_model.SaveOptions(experimental_custom_gradients=False) ile değiştirmeyi denerseniz, gradyan yükleme sırasında yine aynı sonucu verecektir. Bunun nedeni, degrade kaydının hala call_custom_op işlevinde kullanılan özel degradeyi içermesidir. Ancak, özel degradeler olmadan kaydettikten sonra çalışma zamanını yeniden başlatırsanız, yüklenen modeli tf.GradientTape altında çalıştırmak şu hatayı verir: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .
Çoklu bantlar
Birden çok bant sorunsuz bir şekilde etkileşime girer.
Örneğin, burada her bant farklı bir tensör setini izler:
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
Daha yüksek dereceli gradyanlar
tf.GradientTape bağlam yöneticisinin içindeki işlemler, otomatik farklılaşma için kaydedilir. Gradyanlar bu bağlamda hesaplanırsa, gradyan hesaplaması da kaydedilir. Sonuç olarak, aynı API daha yüksek dereceli gradyanlar için de çalışır.
Örneğin:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0 d2y_dx2: 6.0
Bu size bir skaler fonksiyonun ikinci türevini verse de, tf.GradientTape.gradient yalnızca bir skalerin gradyanını hesapladığı için bu model bir Hessian matrisi üretmek için genelleme yapmaz. Bir Hess matrisi oluşturmak için Jacobian bölümü altındaki Hess örneğine gidin.
" tf.GradientTape.gradient için iç içe çağrılar ", bir degradeden bir skaler hesaplarken iyi bir kalıptır ve ardından elde edilen skaler, aşağıdaki örnekte olduğu gibi ikinci bir gradyan hesaplaması için bir kaynak görevi görür.
Örnek: Girdi gradyan düzenlemesi
Pek çok model "karşıt örneklere" karşı hassastır. Bu teknikler koleksiyonu, modelin çıktısını karıştırmak için modelin girdisini değiştirir. Fast Gradient Signed Method saldırısını kullanan Adversarial örneği gibi en basit uygulama, girdiye göre çıktının eğimi boyunca tek bir adım atar; "giriş gradyanı".
Rakip örneklere karşı sağlamlığı artırmaya yönelik bir teknik, girdi gradyanının büyüklüğünü en aza indirmeye çalışan girdi gradyan düzenlemesidir (Finlay & Oberman, 2019). Giriş gradyanı küçükse, çıkıştaki değişim de küçük olmalıdır.
Aşağıda, girdi gradyan düzenlemesinin saf bir uygulaması bulunmaktadır. Uygulama:
- Bir iç bant kullanarak girdiye göre çıktının gradyanını hesaplayın.
- Bu giriş gradyanının büyüklüğünü hesaplayın.
- Modele göre bu büyüklüğün gradyanını hesaplayın.
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
Jacobianlar
Önceki tüm örnekler, bazı kaynak tensör(ler)e göre bir skaler hedefin gradyanlarını aldı.
Jacobian matrisi , vektör değerli bir fonksiyonun gradyanlarını temsil eder. Her satır, vektörün öğelerinden birinin gradyanını içerir.
tf.GradientTape.jacobian yöntemi, bir Jacobian matrisini verimli bir şekilde hesaplamanıza olanak tanır.
Bunu not et:
-
gradientgibi:sourcesargümanı bir tensör veya bir tensör kabı olabilir. -
gradientfarklı olarak:targettensör tek bir tensör olmalıdır.
skaler kaynak
İlk örnek olarak, burada bir vektör hedefinin bir skaler kaynağa göre Jacobian'ı verilmiştir.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
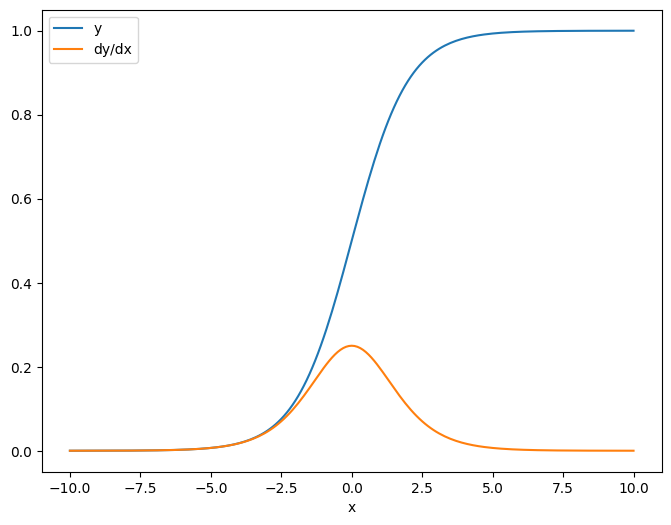
Jacobian'ı bir skalere göre aldığınızda, sonuç hedefin şeklini alır ve her bir öğenin kaynağa göre gradyanını verir:
print(y.shape)
print(dy_dx.shape)
(201,) (201,)-yer tutucu26 l10n-yer
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
Tensör kaynağı
Girdi ister skaler ister tensör olsun, tf.GradientTape.jacobian , hedef(ler)in her bir elemanına göre kaynağın her elemanının gradyanını verimli bir şekilde hesaplar.
Örneğin, bu katmanın çıktısı (10, 7) şeklindedir:
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
Ve katmanın çekirdeğinin şekli (5, 10) :
layer.kernel.shape
TensorShape([5, 10])
Çıktının çekirdeğe göre Jacobian şekli, birlikte birleştirilen bu iki şekildir:
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
Hedefin boyutlarını toplarsanız, tf.GradientTape.gradient tarafından hesaplanacak olan toplamın gradyanı kalır:
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10) delta: 2.3841858e-07
Örnek: Hessen
tf.GradientTape bir Hessian matrisi oluşturmak için açık bir yöntem vermese de tf.GradientTape.jacobian yöntemini kullanarak bir tane oluşturmak mümkündür.
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8) h.shape: (5, 8, 5, 8)
Bu Hessian'ı Newton'un yöntem adımı için kullanmak için, önce eksenlerini bir matriste düzleştirir ve gradyanı bir vektörde düzleştirirsiniz:
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
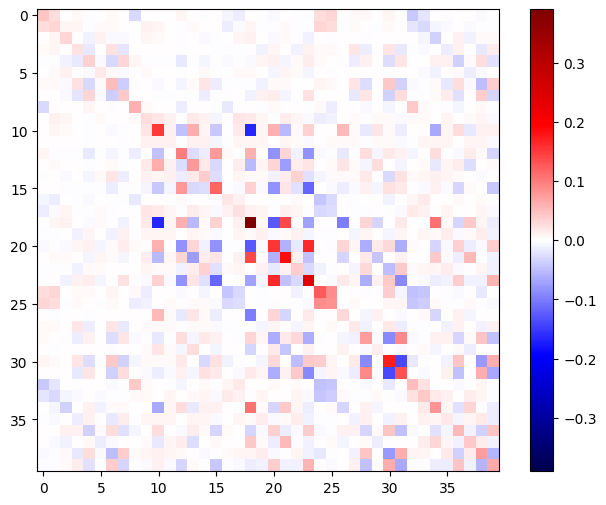
Hessian matrisi simetrik olmalıdır:
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
Newton'un yöntem güncelleme adımı aşağıda gösterilmiştir:
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
Bu, tek bir tf.Variable için nispeten basit olsa da, bunu önemsiz olmayan bir modele uygulamak, birden çok değişken arasında tam bir Hessian üretmek için dikkatli birleştirme ve dilimleme gerektirir.
Toplu Jacobian
Bazı durumlarda, her bir hedef-kaynak çifti için Jacobian'ların bağımsız olduğu bir kaynak yığınına göre bir hedef yığınının her birinin Jacobian'ını almak istersiniz.
Örneğin, burada x girişi şekillendirilir (batch, ins) ve y çıkışı şekillendirilir (batch, outs) :
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
y x göre tam Jacobian'ı, yalnızca isteseniz bile (batch, ins, batch, outs) şeklindedir (batch, ins, outs) :
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
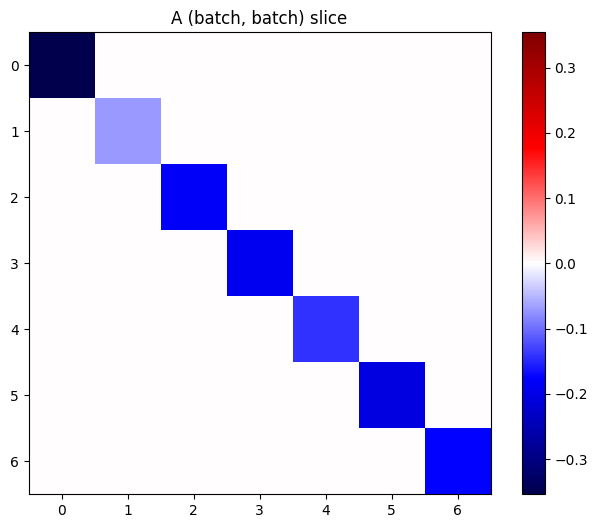
Yığındaki her bir öğenin gradyanları bağımsızsa, bu tensörün her (batch, batch) dilimi bir köşegen matristir:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
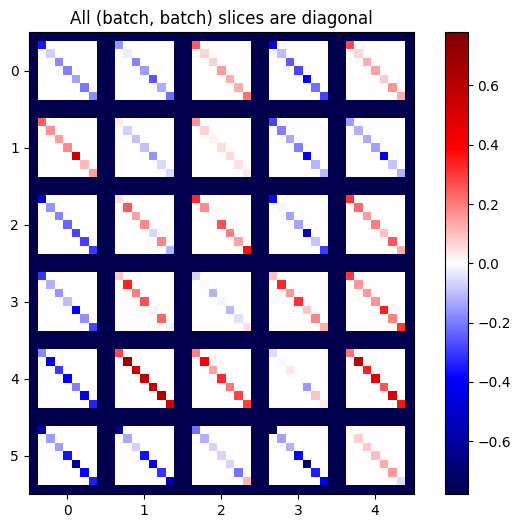
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
İstenen sonucu elde etmek için, yinelenen batch boyutunu toplayabilir veya tf.einsum kullanarak köşegenleri seçebilirsiniz:
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5) (7, 6, 5)
İlk etapta ekstra boyut olmadan hesaplama yapmak çok daha verimli olacaktır. tf.GradientTape.batch_jacobian yöntemi tam olarak şunu yapar:
jb = tape.batch_jacobian(y, x)
jb.shape
WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. TensorShape([7, 6, 5])yer tutucu53 l10n-yer
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. j.shape: (7, 6, 7, 5)-yer tutucu57 l10n-yer
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
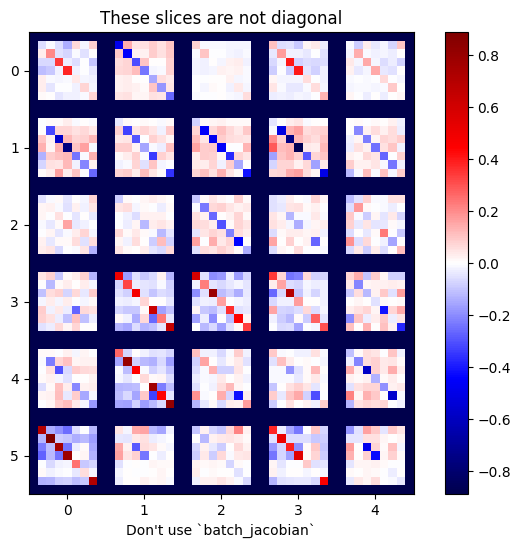
Bu durumda, batch_jacobian yine de çalışır ve beklenen şekle sahip bir şey döndürür, ancak içeriğinin belirsiz bir anlamı vardır:
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)
