Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
JointDistributionSequential adalah distribusi seperti baru diperkenalkan Kelas yang memberdayakan pengguna untuk prototipe cepat Model Bayesian. Ini memungkinkan Anda menghubungkan beberapa distribusi bersama-sama, dan menggunakan fungsi lambda untuk memperkenalkan dependensi. Ini dirancang untuk membangun model Bayesian ukuran kecil hingga menengah, termasuk banyak model yang umum digunakan seperti GLM, model efek campuran, model campuran, dan banyak lagi. Ini memungkinkan semua fitur yang diperlukan untuk alur kerja Bayesian: pengambilan sampel prediktif sebelumnya, Ini bisa menjadi plug-in ke model Grafis Bayesian lain yang lebih besar atau jaringan saraf. Dalam CoLab ini, kami akan menunjukkan beberapa contoh bagaimana menggunakan JointDistributionSequential untuk mencapai hari ke hari Bayesian alur kerja
Dependensi & Prasyarat
# We will be using ArviZ, a multi-backend Bayesian diagnosis and plotting librarypip3 install -q git+git://github.com/arviz-devs/arviz.git
Impor dan set up
from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
import arviz as az
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
sns.reset_defaults()
#sns.set_style('whitegrid')
#sns.set_context('talk')
sns.set_context(context='talk',font_scale=0.7)
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
Membuat hal-hal Cepat!
Sebelum kita masuk, pastikan kita menggunakan GPU untuk demo ini.
Untuk melakukan ini, pilih "Runtime" -> "Ubah jenis runtime" -> "Akselerator perangkat keras" -> "GPU".
Cuplikan berikut akan memverifikasi bahwa kami memiliki akses ke GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Distribusi Bersama
Catatan: Kelas distribusi ini berguna jika Anda hanya memiliki model sederhana. "Sederhana" berarti grafik seperti rantai; meskipun pendekatan ini secara teknis berfungsi untuk PGM apa pun dengan derajat paling banyak 255 untuk satu node (Karena fungsi Python dapat memiliki paling banyak argumen ini).
Ide dasarnya adalah untuk memiliki pengguna menentukan daftar callable s yang menghasilkan tfp.Distribution contoh, satu untuk setiap titik dalam mereka PGM . The callable akan memiliki paling banyak argumen sebagai indeks dalam daftar. (Untuk kenyamanan pengguna, agument akan diteruskan dalam urutan pembuatan terbalik.) Secara internal kami akan "menjalankan grafik" hanya dengan meneruskan setiap nilai RV sebelumnya ke setiap callable. Dengan demikian kita menerapkan [rantai aturan probablity] (https://en.wikipedia.org/wiki/Chain aturan (probabilitas% 29 # More_than_two_random_variables): \(p(\{x\}_i^d)=\prod_i^d p(x_i|x_{<i})\).
Idenya cukup sederhana, bahkan sebagai kode Python. Inilah intinya:
# The chain rule of probability, manifest as Python code.
def log_prob(rvs, xs):
# xs[:i] is rv[i]'s markov blanket. `[::-1]` just reverses the list.
return sum(rv(*xs[i-1::-1]).log_prob(xs[i])
for i, rv in enumerate(rvs))
Anda dapat menemukan informasi lebih lanjut dari docstring dari JointDistributionSequential , tapi intinya adalah bahwa Anda melewati daftar distribusi untuk menginisialisasi Class, jika beberapa distribusi dalam daftar tersebut tergantung pada output dari yang lain distribusi hulu / variabel, Anda hanya membungkusnya dengan fungsi lambda. Sekarang mari kita lihat cara kerjanya dalam tindakan!
(Kuat) Regresi linier
Dari PyMC3 doc GLM: Regresi Robust dengan Outlier Detection
Dapatkan data
dfhogg = pd.DataFrame(np.array([[1, 201, 592, 61, 9, -0.84],
[2, 244, 401, 25, 4, 0.31],
[3, 47, 583, 38, 11, 0.64],
[4, 287, 402, 15, 7, -0.27],
[5, 203, 495, 21, 5, -0.33],
[6, 58, 173, 15, 9, 0.67],
[7, 210, 479, 27, 4, -0.02],
[8, 202, 504, 14, 4, -0.05],
[9, 198, 510, 30, 11, -0.84],
[10, 158, 416, 16, 7, -0.69],
[11, 165, 393, 14, 5, 0.30],
[12, 201, 442, 25, 5, -0.46],
[13, 157, 317, 52, 5, -0.03],
[14, 131, 311, 16, 6, 0.50],
[15, 166, 400, 34, 6, 0.73],
[16, 160, 337, 31, 5, -0.52],
[17, 186, 423, 42, 9, 0.90],
[18, 125, 334, 26, 8, 0.40],
[19, 218, 533, 16, 6, -0.78],
[20, 146, 344, 22, 5, -0.56]]),
columns=['id','x','y','sigma_y','sigma_x','rho_xy'])
## for convenience zero-base the 'id' and use as index
dfhogg['id'] = dfhogg['id'] - 1
dfhogg.set_index('id', inplace=True)
## standardize (mean center and divide by 1 sd)
dfhoggs = (dfhogg[['x','y']] - dfhogg[['x','y']].mean(0)) / dfhogg[['x','y']].std(0)
dfhoggs['sigma_y'] = dfhogg['sigma_y'] / dfhogg['y'].std(0)
dfhoggs['sigma_x'] = dfhogg['sigma_x'] / dfhogg['x'].std(0)
def plot_hoggs(dfhoggs):
## create xlims ylims for plotting
xlims = (dfhoggs['x'].min() - np.ptp(dfhoggs['x'])/5,
dfhoggs['x'].max() + np.ptp(dfhoggs['x'])/5)
ylims = (dfhoggs['y'].min() - np.ptp(dfhoggs['y'])/5,
dfhoggs['y'].max() + np.ptp(dfhoggs['y'])/5)
## scatterplot the standardized data
g = sns.FacetGrid(dfhoggs, size=8)
_ = g.map(plt.errorbar, 'x', 'y', 'sigma_y', 'sigma_x', marker="o", ls='')
_ = g.axes[0][0].set_ylim(ylims)
_ = g.axes[0][0].set_xlim(xlims)
plt.subplots_adjust(top=0.92)
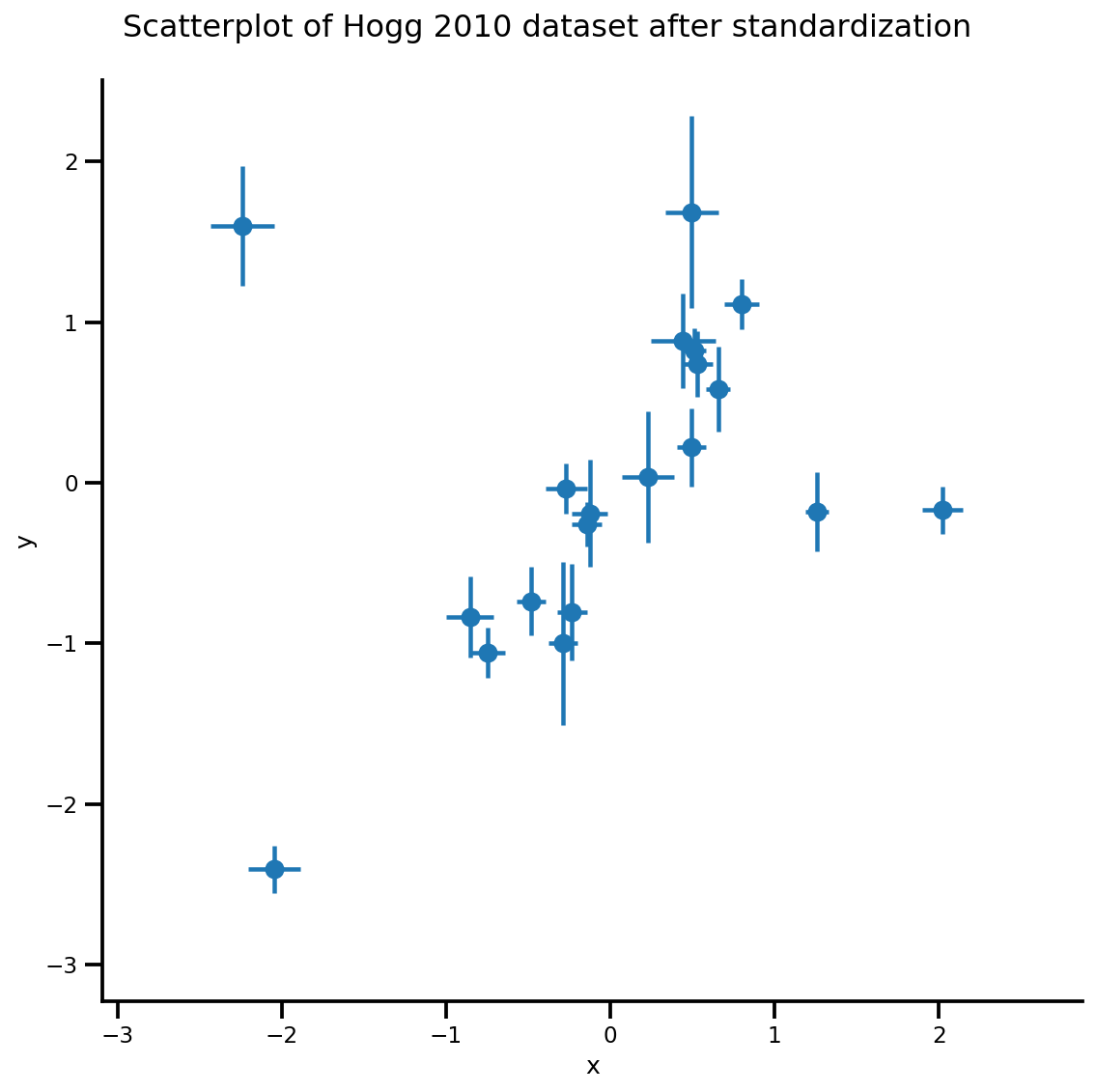
_ = g.fig.suptitle('Scatterplot of Hogg 2010 dataset after standardization', fontsize=16)
return g, xlims, ylims
g = plot_hoggs(dfhoggs)
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
X_np = dfhoggs['x'].values
sigma_y_np = dfhoggs['sigma_y'].values
Y_np = dfhoggs['y'].values
Model OLS Konvensional
Sekarang, mari kita buat model linier, masalah intersep sederhana + regresi kemiringan:
mdl_ols = tfd.JointDistributionSequential([
# b0 ~ Normal(0, 1)
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1 ~ Normal(0, 1)
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# x ~ Normal(b0+b1*X, 1)
lambda b1, b0: tfd.Normal(
# Parameter transformation
loc=b0 + b1*X_np,
scale=sigma_y_np)
])
Anda kemudian dapat memeriksa grafik model untuk melihat ketergantungan. Perhatikan bahwa x dicadangkan sebagai nama node terakhir, dan Anda tidak bisa yakin itu sebagai argumen lambda Anda dalam model JointDistributionSequential Anda.
mdl_ols.resolve_graph()
(('b0', ()), ('b1', ()), ('x', ('b1', 'b0')))
Pengambilan sampel dari model cukup mudah:
mdl_ols.sample()
[<tf.Tensor: shape=(), dtype=float64, numpy=-0.50225804634794>,
<tf.Tensor: shape=(), dtype=float64, numpy=0.682740126293564>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.33051382, 0.71443618, -1.91085683, 0.89371173, -0.45060957,
-1.80448758, -0.21357082, 0.07891058, -0.20689721, -0.62690385,
-0.55225748, -0.11446535, -0.66624497, -0.86913291, -0.93605552,
-0.83965336, -0.70988597, -0.95813437, 0.15884761, -0.31113434])>]
...yang memberikan daftar tf.Tensor. Anda dapat langsung menghubungkannya ke fungsi log_prob untuk menghitung log_prob model:
prior_predictive_samples = mdl_ols.sample()
mdl_ols.log_prob(prior_predictive_samples)
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-4.97502846, -3.98544303, -4.37514505, -3.46933487, -3.80688125,
-3.42907525, -4.03263074, -3.3646366 , -4.70370938, -4.36178501,
-3.47823735, -3.94641662, -5.76906319, -4.0944128 , -4.39310708,
-4.47713894, -4.46307881, -3.98802372, -3.83027747, -4.64777082])>
Hmmm, ada yang tidak beres di sini: kita seharusnya mendapatkan log_prob skalar! Bahkan, kita lebih dapat memeriksa untuk melihat apakah ada sesuatu yang off dengan memanggil .log_prob_parts , yang memberikan log_prob setiap node dalam model grafis:
mdl_ols.log_prob_parts(prior_predictive_samples)
[<tf.Tensor: shape=(), dtype=float64, numpy=-0.9699239562734849>,
<tf.Tensor: shape=(), dtype=float64, numpy=-3.459364167569284>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.54574034, 0.4438451 , 0.05414307, 0.95995326, 0.62240687,
1.00021288, 0.39665739, 1.06465152, -0.27442125, 0.06750311,
0.95105078, 0.4828715 , -1.33977506, 0.33487533, 0.03618104,
-0.04785082, -0.03379069, 0.4412644 , 0.59901066, -0.2184827 ])>]
...ternyata simpul terakhir tidak direduksi_sum di sepanjang dimensi/sumbu iid! Ketika kita melakukan penjumlahan, dua variabel pertama dengan demikian salah disiarkan.
Kuncinya di sini adalah dengan menggunakan tfd.Independent untuk menafsirkan ulang bentuk bets (sehingga sisa sumbu akan berkurang dengan benar):
mdl_ols_ = tfd.JointDistributionSequential([
# b0
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# likelihood
# Using Independent to ensure the log_prob is not incorrectly broadcasted
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
# b1 shape: (batch_shape), X shape (num_obs): we want result to have
# shape (batch_shape, num_obs)
loc=b0 + b1*X_np,
scale=sigma_y_np),
reinterpreted_batch_ndims=1
),
])
Sekarang, mari kita periksa simpul/distribusi terakhir dari model, Anda dapat melihat bahwa bentuk peristiwa sekarang diinterpretasikan dengan benar. Perhatikan bahwa mungkin butuh sedikit trial and error untuk mendapatkan reinterpreted_batch_ndims benar, tetapi Anda dapat selalu dengan mudah mencetak distribusi atau sampel tensor untuk periksa bentuk!
print(mdl_ols_.sample_distributions()[0][-1])
print(mdl_ols.sample_distributions()[0][-1])
tfp.distributions.Independent("JointDistributionSequential_sample_distributions_IndependentJointDistributionSequential_sample_distributions_Normal", batch_shape=[], event_shape=[20], dtype=float64)
tfp.distributions.Normal("JointDistributionSequential_sample_distributions_Normal", batch_shape=[20], event_shape=[], dtype=float64)
prior_predictive_samples = mdl_ols_.sample()
mdl_ols_.log_prob(prior_predictive_samples) # <== Getting a scalar correctly
<tf.Tensor: shape=(), dtype=float64, numpy=-2.543425661013286>
Lainnya JointDistribution* API
mdl_ols_named = tfd.JointDistributionNamed(dict(
likelihood = lambda b0, b1: tfd.Independent(
tfd.Normal(
loc=b0 + b1*X_np,
scale=sigma_y_np),
reinterpreted_batch_ndims=1
),
b0 = tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
b1 = tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
))
mdl_ols_named.log_prob(mdl_ols_named.sample())
<tf.Tensor: shape=(), dtype=float64, numpy=-5.99620966071338>
mdl_ols_named.sample() # output is a dictionary
{'b0': <tf.Tensor: shape=(), dtype=float64, numpy=0.26364058399428225>,
'b1': <tf.Tensor: shape=(), dtype=float64, numpy=-0.27209402374432207>,
'likelihood': <tf.Tensor: shape=(20,), dtype=float64, numpy=
array([ 0.6482155 , -0.39314108, 0.62744764, -0.24587987, -0.20544617,
1.01465392, -0.04705611, -0.16618702, 0.36410134, 0.3943299 ,
0.36455291, -0.27822219, -0.24423928, 0.24599518, 0.82731092,
-0.21983033, 0.56753169, 0.32830481, -0.15713064, 0.23336351])>}
Root = tfd.JointDistributionCoroutine.Root # Convenient alias.
def model():
b1 = yield Root(tfd.Normal(loc=tf.cast(0, dtype), scale=1.))
b0 = yield Root(tfd.Normal(loc=tf.cast(0, dtype), scale=1.))
yhat = b0 + b1*X_np
likelihood = yield tfd.Independent(
tfd.Normal(loc=yhat, scale=sigma_y_np),
reinterpreted_batch_ndims=1
)
mdl_ols_coroutine = tfd.JointDistributionCoroutine(model)
mdl_ols_coroutine.log_prob(mdl_ols_coroutine.sample())
<tf.Tensor: shape=(), dtype=float64, numpy=-4.566678123520463>
mdl_ols_coroutine.sample() # output is a tuple
(<tf.Tensor: shape=(), dtype=float64, numpy=0.06811002171170354>,
<tf.Tensor: shape=(), dtype=float64, numpy=-0.37477064754116807>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.91615096, -0.20244718, -0.47840159, -0.26632479, -0.60441105,
-0.48977789, -0.32422329, -0.44019322, -0.17072643, -0.20666025,
-0.55932191, -0.40801868, -0.66893181, -0.24134135, -0.50403536,
-0.51788596, -0.90071876, -0.47382338, -0.34821655, -0.38559724])>)
MLE
Dan sekarang kita bisa melakukan inferensi! Anda dapat menggunakan pengoptimal untuk menemukan estimasi kemungkinan Maksimum.
Tentukan beberapa fungsi pembantu
# bfgs and lbfgs currently requries a function that returns both the value and
# gradient re the input.
import functools
def _make_val_and_grad_fn(value_fn):
@functools.wraps(value_fn)
def val_and_grad(x):
return tfp.math.value_and_gradient(value_fn, x)
return val_and_grad
# Map a list of tensors (e.g., output from JDSeq.sample([...])) to a single tensor
# modify from tfd.Blockwise
from tensorflow_probability.python.internal import dtype_util
from tensorflow_probability.python.internal import prefer_static as ps
from tensorflow_probability.python.internal import tensorshape_util
class Mapper:
"""Basically, this is a bijector without log-jacobian correction."""
def __init__(self, list_of_tensors, list_of_bijectors, event_shape):
self.dtype = dtype_util.common_dtype(
list_of_tensors, dtype_hint=tf.float32)
self.list_of_tensors = list_of_tensors
self.bijectors = list_of_bijectors
self.event_shape = event_shape
def flatten_and_concat(self, list_of_tensors):
def _reshape_map_part(part, event_shape, bijector):
part = tf.cast(bijector.inverse(part), self.dtype)
static_rank = tf.get_static_value(ps.rank_from_shape(event_shape))
if static_rank == 1:
return part
new_shape = ps.concat([
ps.shape(part)[:ps.size(ps.shape(part)) - ps.size(event_shape)],
[-1]
], axis=-1)
return tf.reshape(part, ps.cast(new_shape, tf.int32))
x = tf.nest.map_structure(_reshape_map_part,
list_of_tensors,
self.event_shape,
self.bijectors)
return tf.concat(tf.nest.flatten(x), axis=-1)
def split_and_reshape(self, x):
assertions = []
message = 'Input must have at least one dimension.'
if tensorshape_util.rank(x.shape) is not None:
if tensorshape_util.rank(x.shape) == 0:
raise ValueError(message)
else:
assertions.append(assert_util.assert_rank_at_least(x, 1, message=message))
with tf.control_dependencies(assertions):
splits = [
tf.cast(ps.maximum(1, ps.reduce_prod(s)), tf.int32)
for s in tf.nest.flatten(self.event_shape)
]
x = tf.nest.pack_sequence_as(
self.event_shape, tf.split(x, splits, axis=-1))
def _reshape_map_part(part, part_org, event_shape, bijector):
part = tf.cast(bijector.forward(part), part_org.dtype)
static_rank = tf.get_static_value(ps.rank_from_shape(event_shape))
if static_rank == 1:
return part
new_shape = ps.concat([ps.shape(part)[:-1], event_shape], axis=-1)
return tf.reshape(part, ps.cast(new_shape, tf.int32))
x = tf.nest.map_structure(_reshape_map_part,
x,
self.list_of_tensors,
self.event_shape,
self.bijectors)
return x
mapper = Mapper(mdl_ols_.sample()[:-1],
[tfb.Identity(), tfb.Identity()],
mdl_ols_.event_shape[:-1])
# mapper.split_and_reshape(mapper.flatten_and_concat(mdl_ols_.sample()[:-1]))
@_make_val_and_grad_fn
def neg_log_likelihood(x):
# Generate a function closure so that we are computing the log_prob
# conditioned on the observed data. Note also that tfp.optimizer.* takes a
# single tensor as input.
return -mdl_ols_.log_prob(mapper.split_and_reshape(x) + [Y_np])
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
initial_position=tf.zeros(2, dtype=dtype),
tolerance=1e-20,
x_tolerance=1e-8
)
b0est, b1est = lbfgs_results.position.numpy()
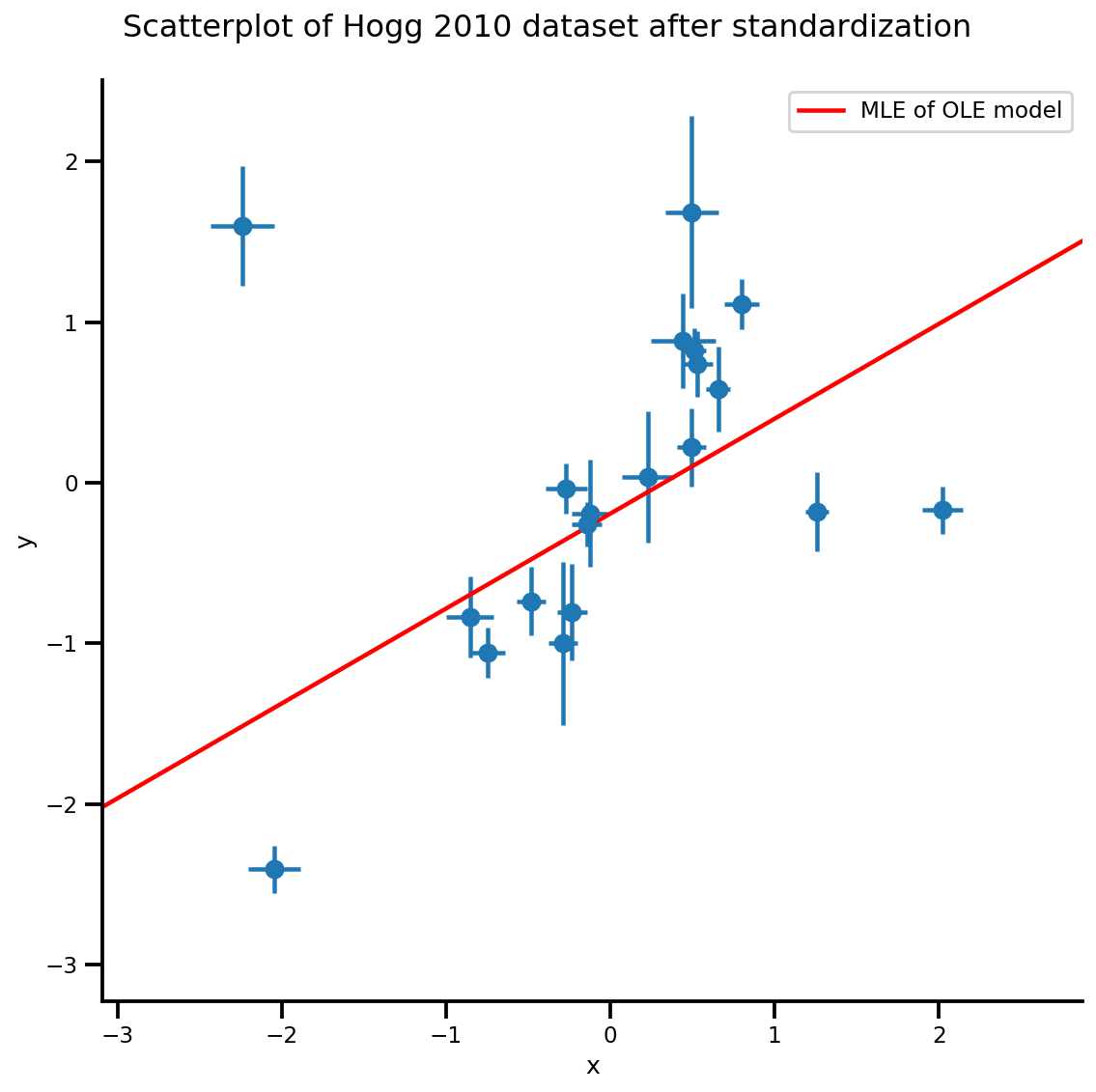
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)
g.axes[0][0].plot(xrange, b0est + b1est*xrange,
color='r', label='MLE of OLE model')
plt.legend();
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
Model versi batch dan MCMC
Dalam Bayesian Inference, kita biasanya ingin bekerja dengan sampel MCMC, seperti ketika sampel berasal dari posterior, kita dapat plug mereka ke fungsi dengan harapan menghitung. Namun, MCMC API mengharuskan kita untuk menulis model yang batch yang ramah, dan kami dapat memeriksa bahwa model kami sebenarnya tidak "batchable" dengan memanggil sample([...])
mdl_ols_.sample(5) # <== error as some computation could not be broadcasted.
Dalam hal ini, relatif mudah karena kita hanya memiliki fungsi linier di dalam model kita, memperluas bentuknya akan berhasil:
mdl_ols_batch = tfd.JointDistributionSequential([
# b0
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# likelihood
# Using Independent to ensure the log_prob is not incorrectly broadcasted
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
loc=b0[..., tf.newaxis] + b1[..., tf.newaxis]*X_np[tf.newaxis, ...],
scale=sigma_y_np[tf.newaxis, ...]),
reinterpreted_batch_ndims=1
),
])
mdl_ols_batch.resolve_graph()
(('b0', ()), ('b1', ()), ('x', ('b1', 'b0')))
Kami kembali dapat mengambil sampel dan mengevaluasi log_prob_parts untuk melakukan beberapa pemeriksaan:
b0, b1, y = mdl_ols_batch.sample(4)
mdl_ols_batch.log_prob_parts([b0, b1, y])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.25230168, -1.45281432, -1.87110061, -1.07665206])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.07019936, -1.59562117, -2.53387765, -1.01557632])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([ 0.45841406, 2.56829635, -4.84973951, -5.59423992])>]
Beberapa catatan samping:
- Kami ingin bekerja dengan model versi batch karena ini adalah yang tercepat untuk MCMC multi-rantai. Dalam kasus yang Anda tidak dapat menulis ulang model sebagai versi batched (misalnya, model ODE), Anda dapat memetakan fungsi log_prob menggunakan
tf.map_fnuntuk mencapai efek yang sama. - Sekarang
mdl_ols_batch.sample()mungkin tidak bekerja seperti yang telah kita scaler sebelumnya, karena kita tidak bisa melakukanscaler_tensor[:, None]. Solusi di sini adalah untuk memperluas tensor scaler ke peringkat 1 dengan pembungkustfd.Sample(..., sample_shape=1). - Ini adalah praktik yang baik untuk menulis model sebagai fungsi sehingga Anda dapat mengubah pengaturan seperti hyperparameter dengan lebih mudah.
def gen_ols_batch_model(X, sigma, hyperprior_mean=0, hyperprior_scale=1):
hyper_mean = tf.cast(hyperprior_mean, dtype)
hyper_scale = tf.cast(hyperprior_scale, dtype)
return tfd.JointDistributionSequential([
# b0
tfd.Sample(tfd.Normal(loc=hyper_mean, scale=hyper_scale), sample_shape=1),
# b1
tfd.Sample(tfd.Normal(loc=hyper_mean, scale=hyper_scale), sample_shape=1),
# likelihood
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
loc=b0 + b1*X,
scale=sigma),
reinterpreted_batch_ndims=1
),
], validate_args=True)
mdl_ols_batch = gen_ols_batch_model(X_np[tf.newaxis, ...],
sigma_y_np[tf.newaxis, ...])
_ = mdl_ols_batch.sample()
_ = mdl_ols_batch.sample(4)
_ = mdl_ols_batch.sample([3, 4])
# Small helper function to validate log_prob shape (avoid wrong broadcasting)
def validate_log_prob_part(model, batch_shape=1, observed=-1):
samples = model.sample(batch_shape)
logp_part = list(model.log_prob_parts(samples))
# exclude observed node
logp_part.pop(observed)
for part in logp_part:
tf.assert_equal(part.shape, logp_part[-1].shape)
validate_log_prob_part(mdl_ols_batch, 4)
Pemeriksaan lebih lanjut: membandingkan fungsi log_prob yang dihasilkan dengan fungsi log_prob TFP tulisan tangan.
def ols_logp_batch(b0, b1, Y):
b0_prior = tfd.Normal(loc=tf.cast(0, dtype), scale=1.) # b0
b1_prior = tfd.Normal(loc=tf.cast(0, dtype), scale=1.) # b1
likelihood = tfd.Normal(loc=b0 + b1*X_np[None, :],
scale=sigma_y_np) # likelihood
return tf.reduce_sum(b0_prior.log_prob(b0), axis=-1) +\
tf.reduce_sum(b1_prior.log_prob(b1), axis=-1) +\
tf.reduce_sum(likelihood.log_prob(Y), axis=-1)
b0, b1, x = mdl_ols_batch.sample(4)
print(mdl_ols_batch.log_prob([b0, b1, Y_np]).numpy())
print(ols_logp_batch(b0, b1, Y_np).numpy())
[-227.37899384 -327.10043743 -570.44162789 -702.79808683] [-227.37899384 -327.10043743 -570.44162789 -702.79808683]
MCMC menggunakan Sampler Tanpa Putar
Sebuah umum run_chain fungsi
@tf.function(autograph=False, experimental_compile=True)
def run_chain(init_state, step_size, target_log_prob_fn, unconstraining_bijectors,
num_steps=500, burnin=50):
def trace_fn(_, pkr):
return (
pkr.inner_results.inner_results.target_log_prob,
pkr.inner_results.inner_results.leapfrogs_taken,
pkr.inner_results.inner_results.has_divergence,
pkr.inner_results.inner_results.energy,
pkr.inner_results.inner_results.log_accept_ratio
)
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.NoUTurnSampler(
target_log_prob_fn,
step_size=step_size),
bijector=unconstraining_bijectors)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=burnin,
step_size_setter_fn=lambda pkr, new_step_size: pkr._replace(
inner_results=pkr.inner_results._replace(step_size=new_step_size)),
step_size_getter_fn=lambda pkr: pkr.inner_results.step_size,
log_accept_prob_getter_fn=lambda pkr: pkr.inner_results.log_accept_ratio
)
# Sampling from the chain.
chain_state, sampler_stat = tfp.mcmc.sample_chain(
num_results=num_steps,
num_burnin_steps=burnin,
current_state=init_state,
kernel=hmc,
trace_fn=trace_fn)
return chain_state, sampler_stat
nchain = 10
b0, b1, _ = mdl_ols_batch.sample(nchain)
init_state = [b0, b1]
step_size = [tf.cast(i, dtype=dtype) for i in [.1, .1]]
target_log_prob_fn = lambda *x: mdl_ols_batch.log_prob(x + (Y_np, ))
# bijector to map contrained parameters to real
unconstraining_bijectors = [
tfb.Identity(),
tfb.Identity(),
]
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['b0', 'b1']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
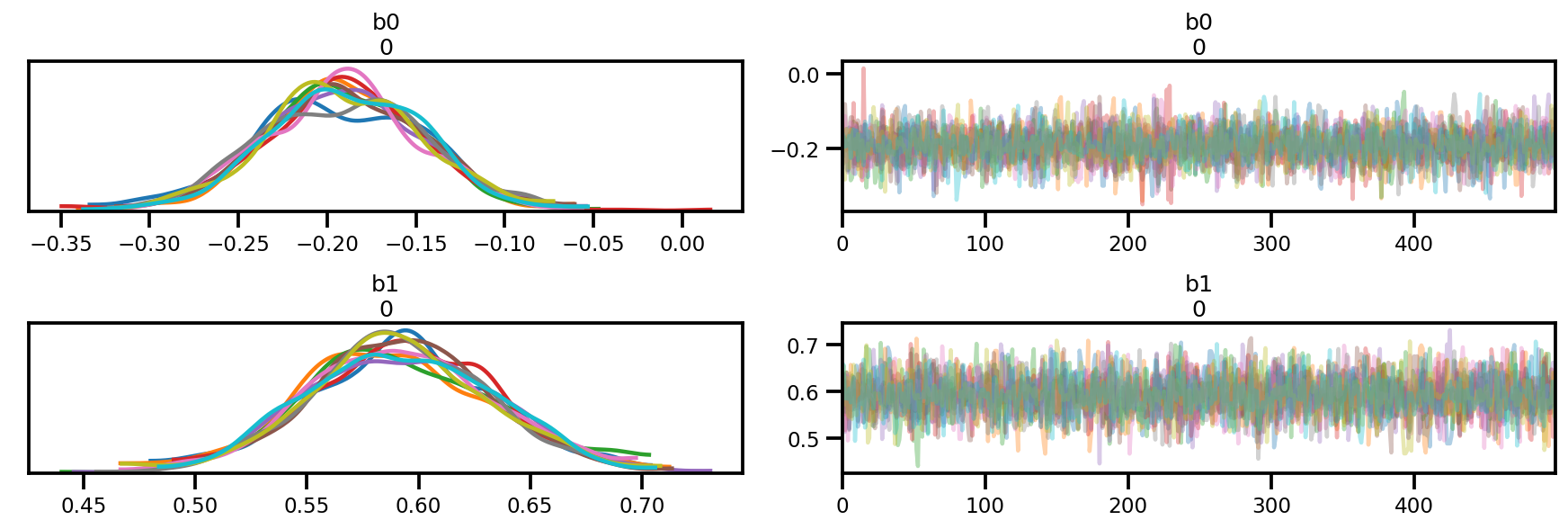
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.plot_trace(az_trace);
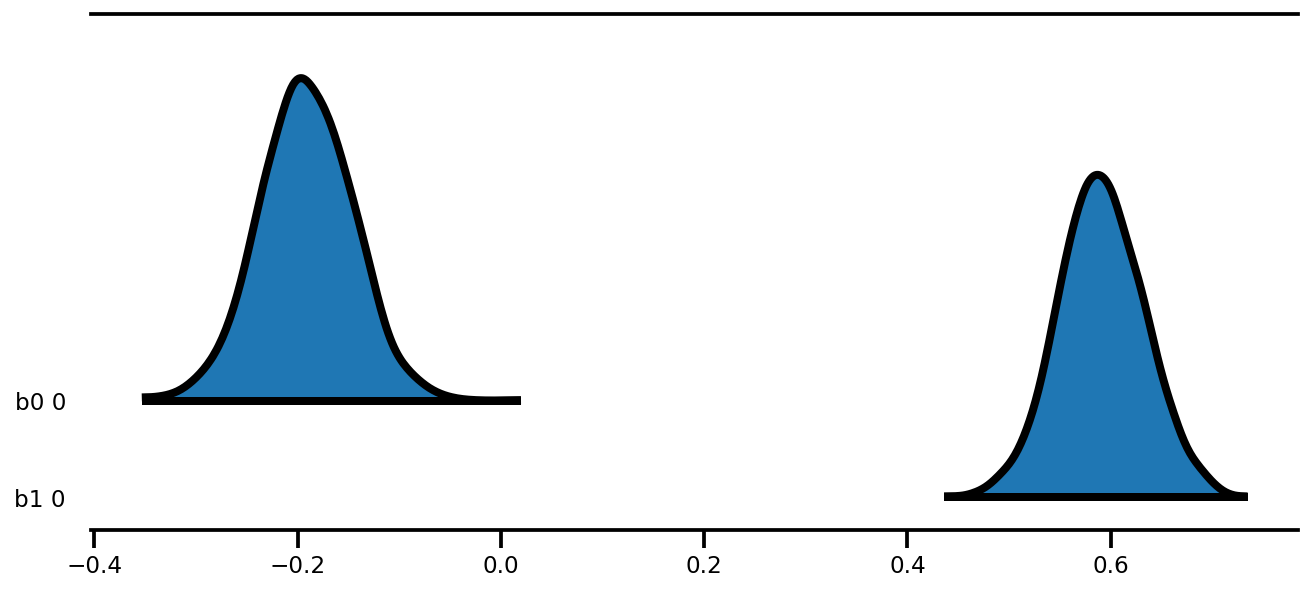
az.plot_forest(az_trace,
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 4));
k = 5
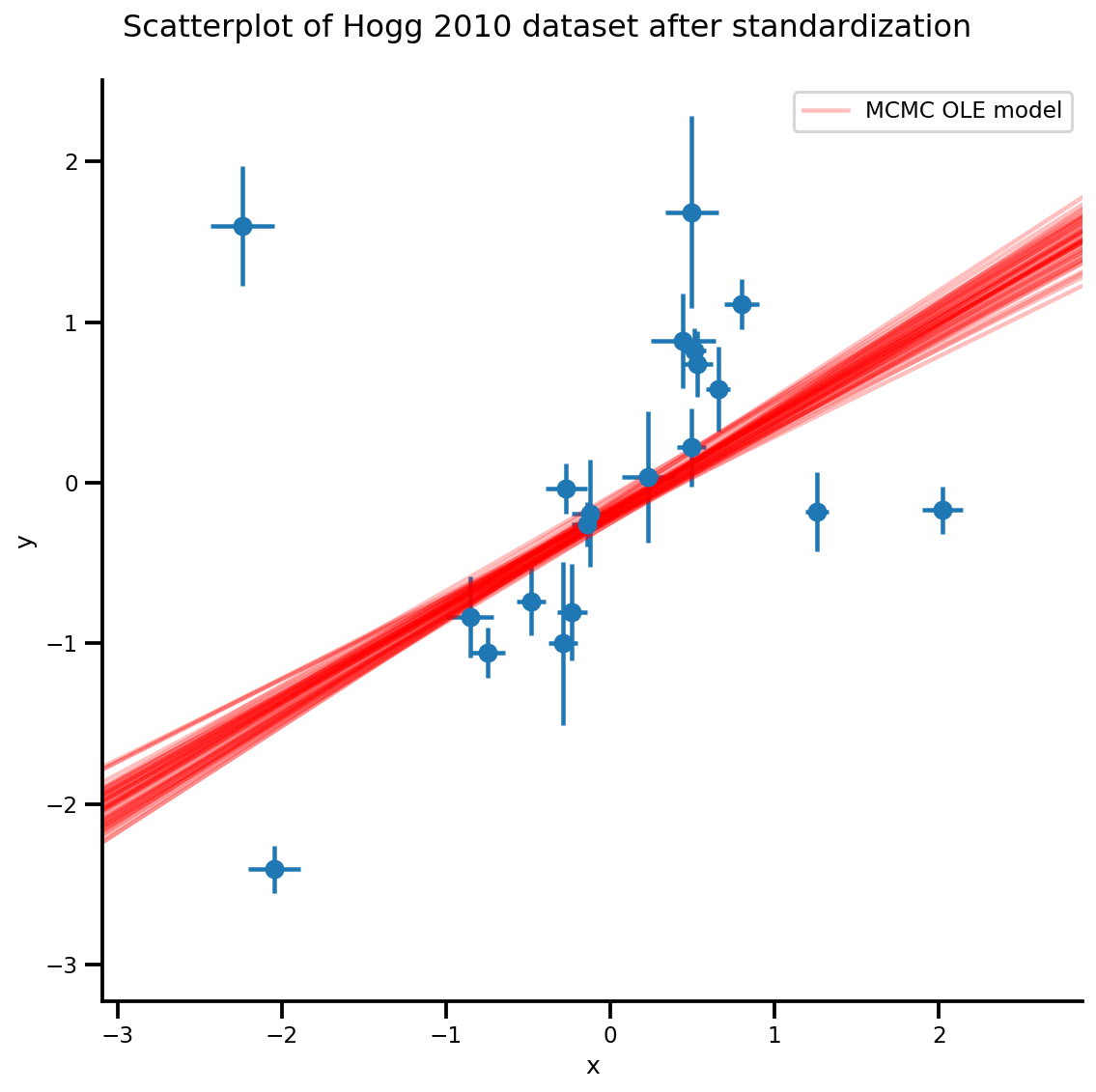
b0est, b1est = az_trace.posterior['b0'][:, -k:].values, az_trace.posterior['b1'][:, -k:].values
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)[None, :]
g.axes[0][0].plot(np.tile(xrange, (k, 1)).T,
(np.reshape(b0est, [-1, 1]) + np.reshape(b1est, [-1, 1])*xrange).T,
alpha=.25, color='r')
plt.legend([g.axes[0][0].lines[-1]], ['MCMC OLE model']);
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning) /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:8: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.
Metode Student-T
Perhatikan bahwa mulai sekarang kami selalu bekerja dengan model versi batch
def gen_studentt_model(X, sigma,
hyper_mean=0, hyper_scale=1, lower=1, upper=100):
loc = tf.cast(hyper_mean, dtype)
scale = tf.cast(hyper_scale, dtype)
low = tf.cast(lower, dtype)
high = tf.cast(upper, dtype)
return tfd.JointDistributionSequential([
# b0 ~ Normal(0, 1)
tfd.Sample(tfd.Normal(loc, scale), sample_shape=1),
# b1 ~ Normal(0, 1)
tfd.Sample(tfd.Normal(loc, scale), sample_shape=1),
# df ~ Uniform(a, b)
tfd.Sample(tfd.Uniform(low, high), sample_shape=1),
# likelihood ~ StudentT(df, f(b0, b1), sigma_y)
# Using Independent to ensure the log_prob is not incorrectly broadcasted.
lambda df, b1, b0: tfd.Independent(
tfd.StudentT(df=df, loc=b0 + b1*X, scale=sigma)),
], validate_args=True)
mdl_studentt = gen_studentt_model(X_np[tf.newaxis, ...],
sigma_y_np[tf.newaxis, ...])
mdl_studentt.resolve_graph()
(('b0', ()), ('b1', ()), ('df', ()), ('x', ('df', 'b1', 'b0')))
validate_log_prob_part(mdl_studentt, 4)
Sampel ke depan (sampling prediktif sebelumnya)
b0, b1, df, x = mdl_studentt.sample(1000)
x.shape
TensorShape([1000, 20])
MLE
# bijector to map contrained parameters to real
a, b = tf.constant(1., dtype), tf.constant(100., dtype),
# Interval transformation
tfp_interval = tfb.Inline(
inverse_fn=(
lambda x: tf.math.log(x - a) - tf.math.log(b - x)),
forward_fn=(
lambda y: (b - a) * tf.sigmoid(y) + a),
forward_log_det_jacobian_fn=(
lambda x: tf.math.log(b - a) - 2 * tf.nn.softplus(-x) - x),
forward_min_event_ndims=0,
name="interval")
unconstraining_bijectors = [
tfb.Identity(),
tfb.Identity(),
tfp_interval,
]
mapper = Mapper(mdl_studentt.sample()[:-1],
unconstraining_bijectors,
mdl_studentt.event_shape[:-1])
@_make_val_and_grad_fn
def neg_log_likelihood(x):
# Generate a function closure so that we are computing the log_prob
# conditioned on the observed data. Note also that tfp.optimizer.* takes a
# single tensor as input, so we need to do some slicing here:
return -tf.squeeze(mdl_studentt.log_prob(
mapper.split_and_reshape(x) + [Y_np]))
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
initial_position=mapper.flatten_and_concat(mdl_studentt.sample()[:-1]),
tolerance=1e-20,
x_tolerance=1e-20
)
b0est, b1est, dfest = lbfgs_results.position.numpy()
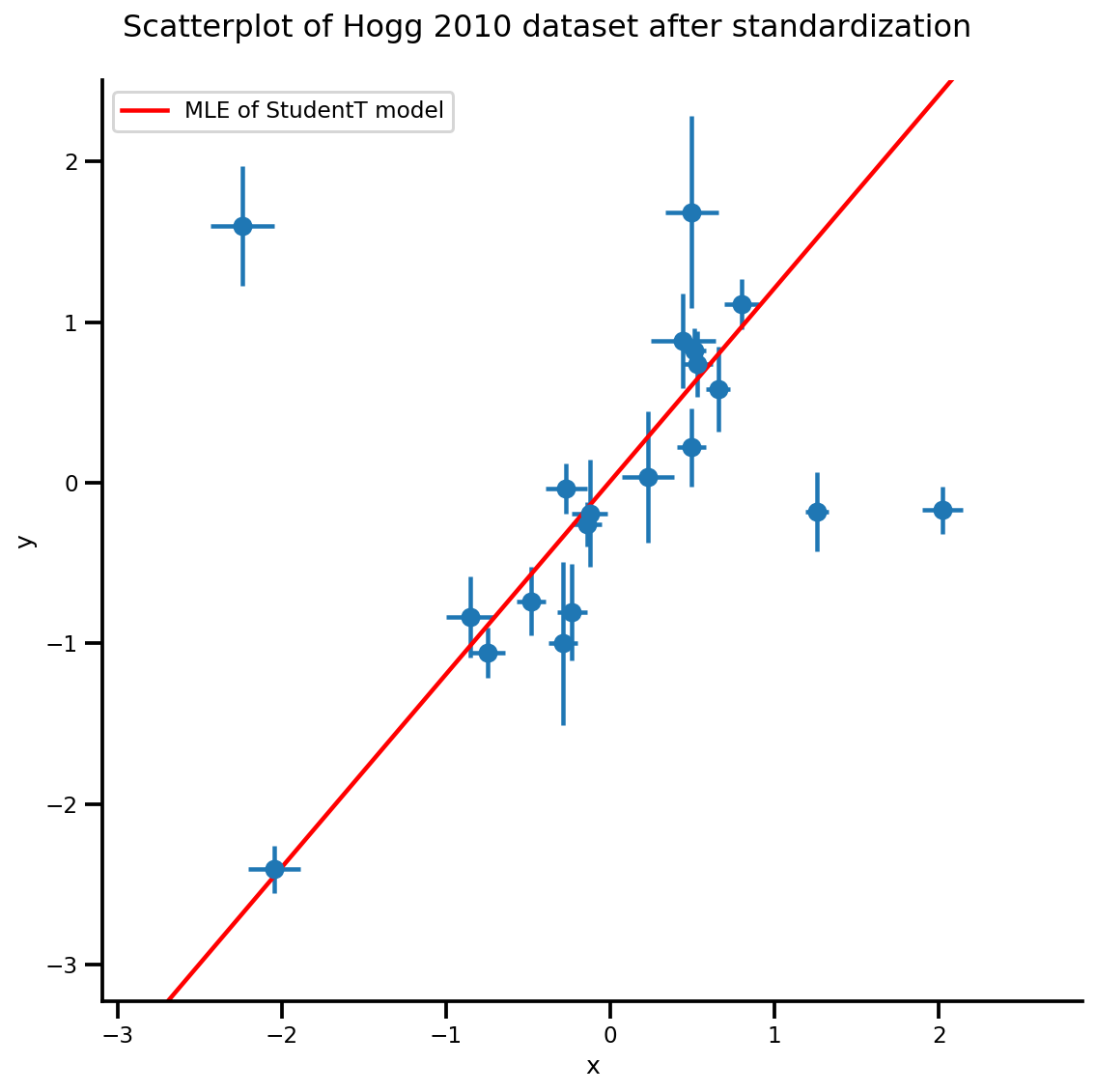
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)
g.axes[0][0].plot(xrange, b0est + b1est*xrange,
color='r', label='MLE of StudentT model')
plt.legend();
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
MCMC
nchain = 10
b0, b1, df, _ = mdl_studentt.sample(nchain)
init_state = [b0, b1, df]
step_size = [tf.cast(i, dtype=dtype) for i in [.1, .1, .05]]
target_log_prob_fn = lambda *x: mdl_studentt.log_prob(x + (Y_np, ))
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors, burnin=100)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['b0', 'b1', 'df']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.summary(az_trace)
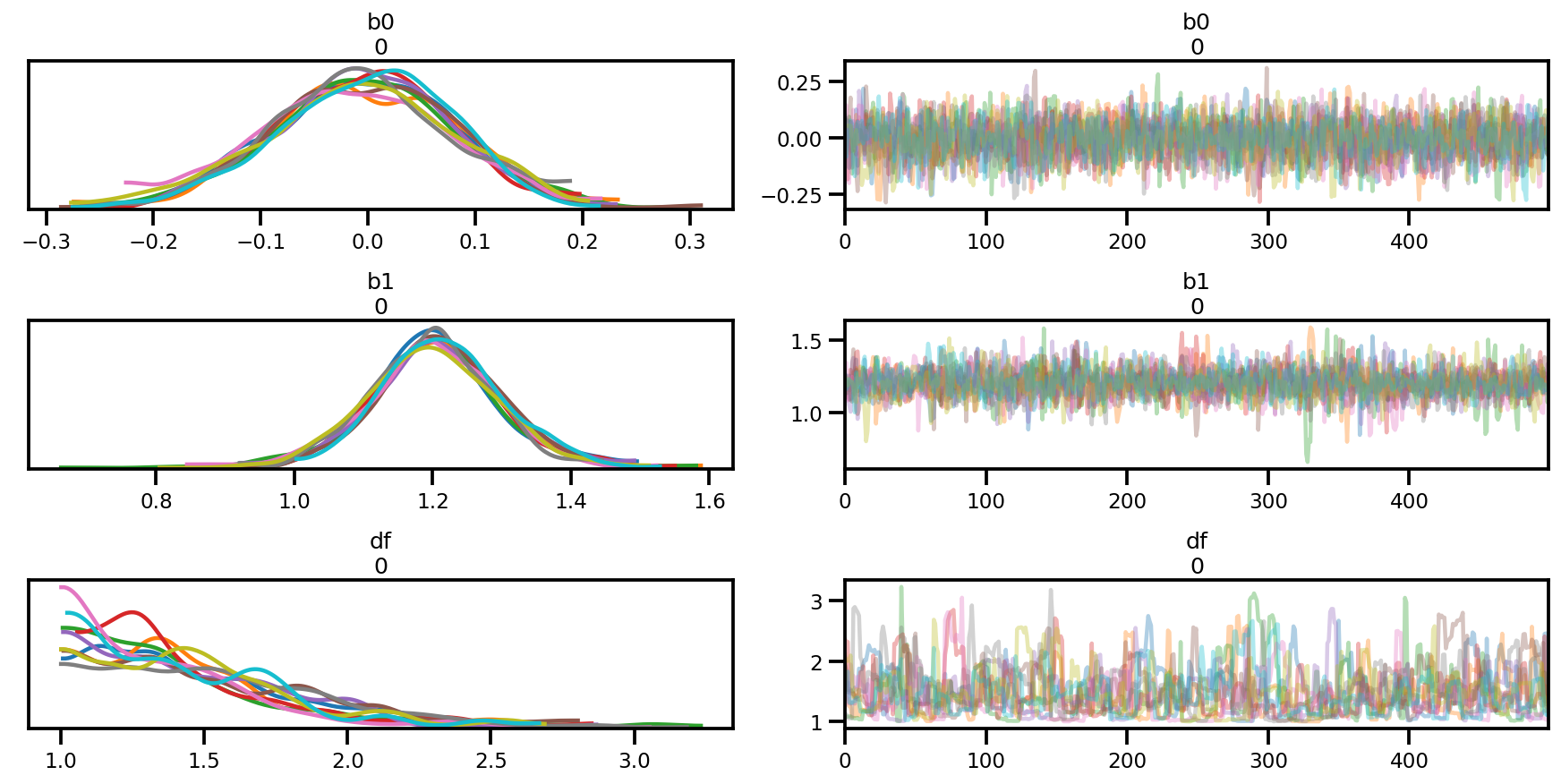
az.plot_trace(az_trace);
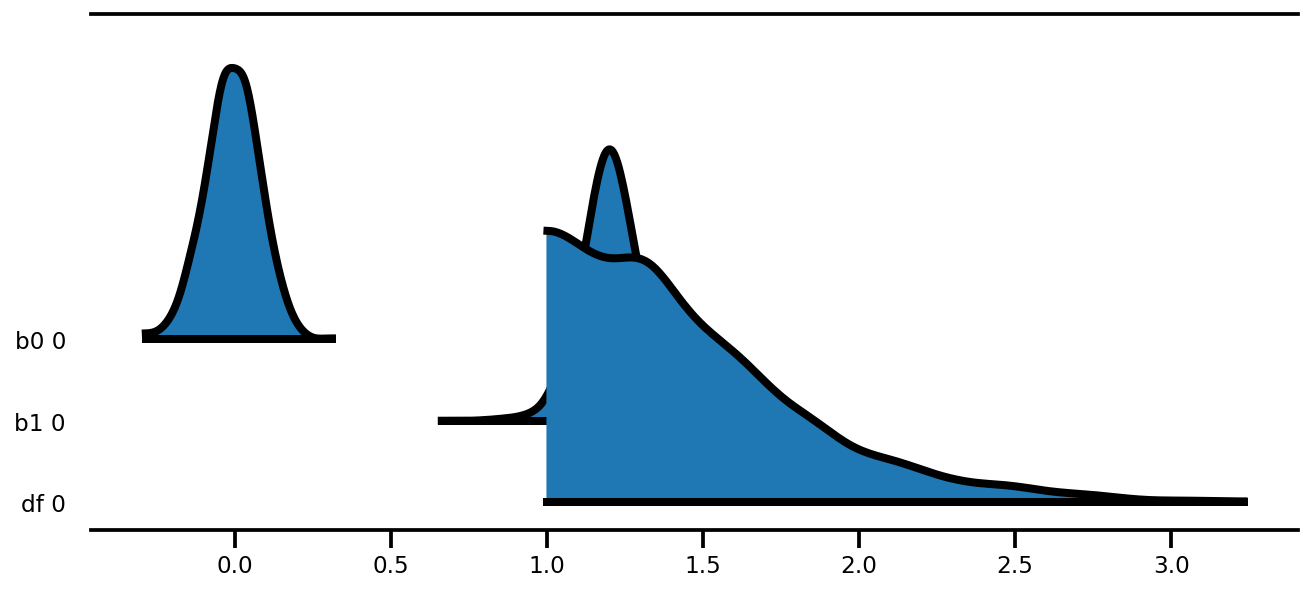
az.plot_forest(az_trace,
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 4));
plt.hist(az_trace.sample_stats['tree_size'], np.linspace(.5, 25.5, 26), alpha=.5);
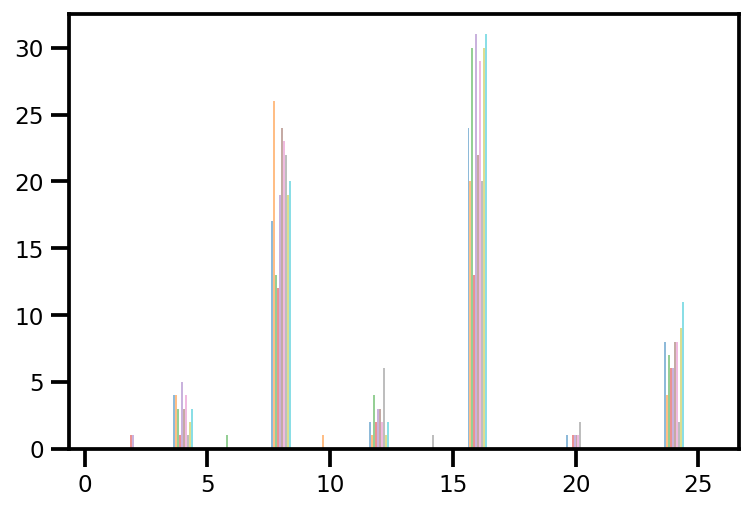
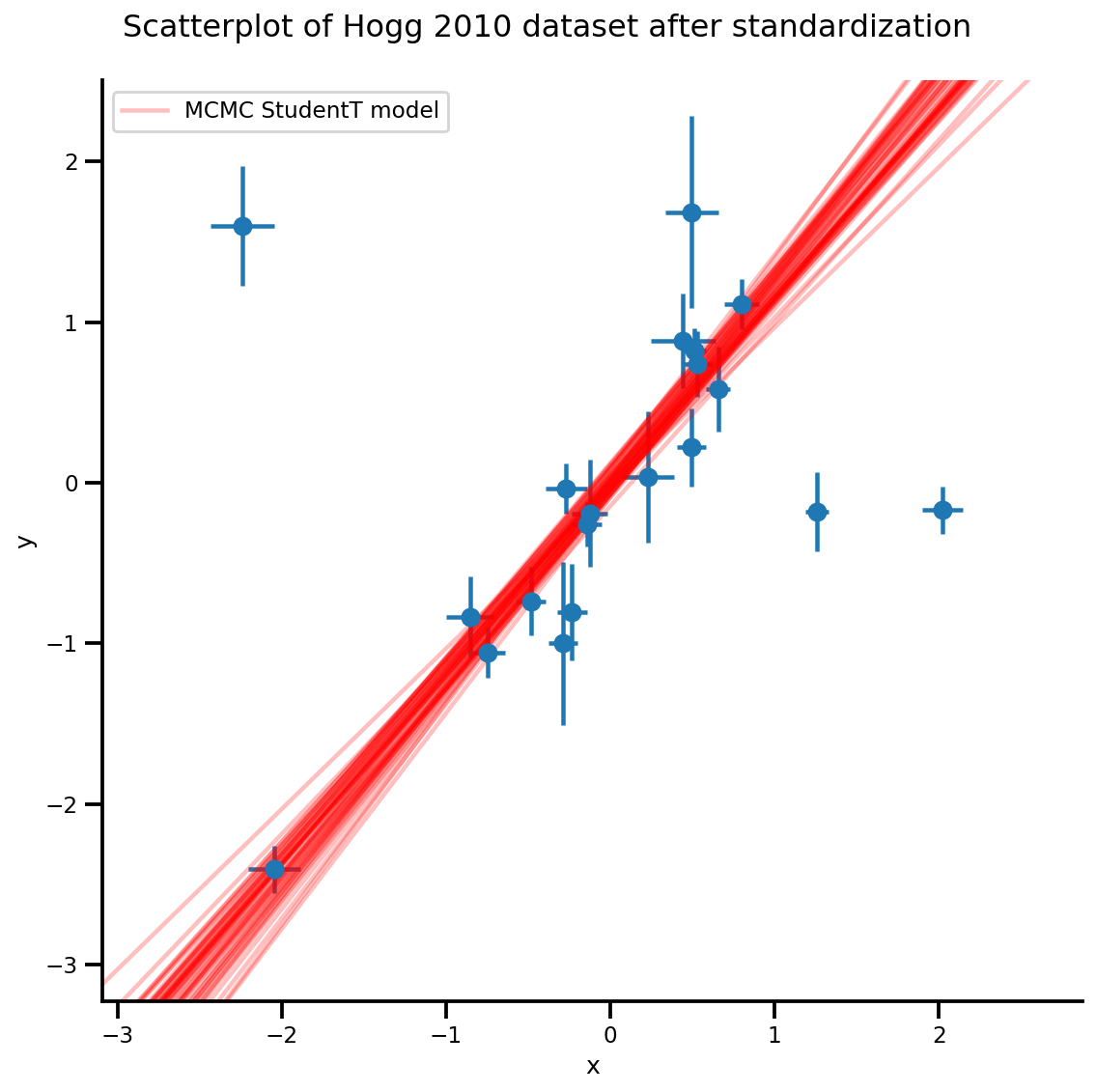
k = 5
b0est, b1est = az_trace.posterior['b0'][:, -k:].values, az_trace.posterior['b1'][:, -k:].values
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)[None, :]
g.axes[0][0].plot(np.tile(xrange, (k, 1)).T,
(np.reshape(b0est, [-1, 1]) + np.reshape(b1est, [-1, 1])*xrange).T,
alpha=.25, color='r')
plt.legend([g.axes[0][0].lines[-1]], ['MCMC StudentT model']);
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning) /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:8: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.
Pengumpulan Parsial Hirarkis
Dari PyMC3 Data bisbol selama 18 pemain dari Efron dan Morris (1975)
data = pd.read_table('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/efron-morris-75-data.tsv',
sep="\t")
at_bats, hits = data[['At-Bats', 'Hits']].values.T
n = len(at_bats)
def gen_baseball_model(at_bats, rate=1.5, a=0, b=1):
return tfd.JointDistributionSequential([
# phi
tfd.Uniform(low=tf.cast(a, dtype), high=tf.cast(b, dtype)),
# kappa_log
tfd.Exponential(rate=tf.cast(rate, dtype)),
# thetas
lambda kappa_log, phi: tfd.Sample(
tfd.Beta(
concentration1=tf.exp(kappa_log)*phi,
concentration0=tf.exp(kappa_log)*(1.0-phi)),
sample_shape=n
),
# likelihood
lambda thetas: tfd.Independent(
tfd.Binomial(
total_count=tf.cast(at_bats, dtype),
probs=thetas
)),
])
mdl_baseball = gen_baseball_model(at_bats)
mdl_baseball.resolve_graph()
(('phi', ()),
('kappa_log', ()),
('thetas', ('kappa_log', 'phi')),
('x', ('thetas',)))
Sampel ke depan (sampling prediktif sebelumnya)
phi, kappa_log, thetas, y = mdl_baseball.sample(4)
# phi, kappa_log, thetas, y
Sekali lagi, perhatikan bagaimana jika Anda tidak menggunakan Independen Anda akan berakhir dengan log_prob yang memiliki batch_shape yang salah.
# check logp
pprint(mdl_baseball.log_prob_parts([phi, kappa_log, thetas, hits]))
print(mdl_baseball.log_prob([phi, kappa_log, thetas, hits]))
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([0., 0., 0., 0.])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([ 0.1721297 , -0.95946498, -0.72591188, 0.23993813])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([59.35192283, 7.0650634 , 0.83744911, 74.14370935])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-3279.75191016, -931.10438484, -512.59197688, -1131.08043597])>] tf.Tensor([-3220.22785762 -924.99878641 -512.48043966 -1056.69678849], shape=(4,), dtype=float64)
MLE
Sebuah fitur menakjubkan dari tfp.optimizer adalah bahwa, Anda dapat dioptimalkan secara paralel untuk k batch titik awal dan menentukan stopping_condition kwarg: Anda dapat mengaturnya untuk tfp.optimizer.converged_all untuk melihat apakah mereka semua menemukan yang sama minimal, atau tfp.optimizer.converged_any untuk menemukan solusi lokal cepat.
unconstraining_bijectors = [
tfb.Sigmoid(),
tfb.Exp(),
tfb.Sigmoid(),
]
phi, kappa_log, thetas, y = mdl_baseball.sample(10)
mapper = Mapper([phi, kappa_log, thetas],
unconstraining_bijectors,
mdl_baseball.event_shape[:-1])
@_make_val_and_grad_fn
def neg_log_likelihood(x):
return -mdl_baseball.log_prob(mapper.split_and_reshape(x) + [hits])
start = mapper.flatten_and_concat([phi, kappa_log, thetas])
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
num_correction_pairs=10,
initial_position=start,
# lbfgs actually can work in batch as well
stopping_condition=tfp.optimizer.converged_any,
tolerance=1e-50,
x_tolerance=1e-50,
parallel_iterations=10,
max_iterations=200
)
lbfgs_results.converged.numpy(), lbfgs_results.failed.numpy()
(array([False, False, False, False, False, False, False, False, False,
False]),
array([ True, True, True, True, True, True, True, True, True,
True]))
result = lbfgs_results.position[lbfgs_results.converged & ~lbfgs_results.failed]
result
<tf.Tensor: shape=(0, 20), dtype=float64, numpy=array([], shape=(0, 20), dtype=float64)>
LBFGS tidak konvergen.
if result.shape[0] > 0:
phi_est, kappa_est, theta_est = mapper.split_and_reshape(result)
phi_est, kappa_est, theta_est
MCMC
target_log_prob_fn = lambda *x: mdl_baseball.log_prob(x + (hits, ))
nchain = 4
phi, kappa_log, thetas, _ = mdl_baseball.sample(nchain)
init_state = [phi, kappa_log, thetas]
step_size=[tf.cast(i, dtype=dtype) for i in [.1, .1, .1]]
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors,
burnin=200)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['phi', 'kappa_log', 'thetas']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.plot_trace(az_trace, compact=True);
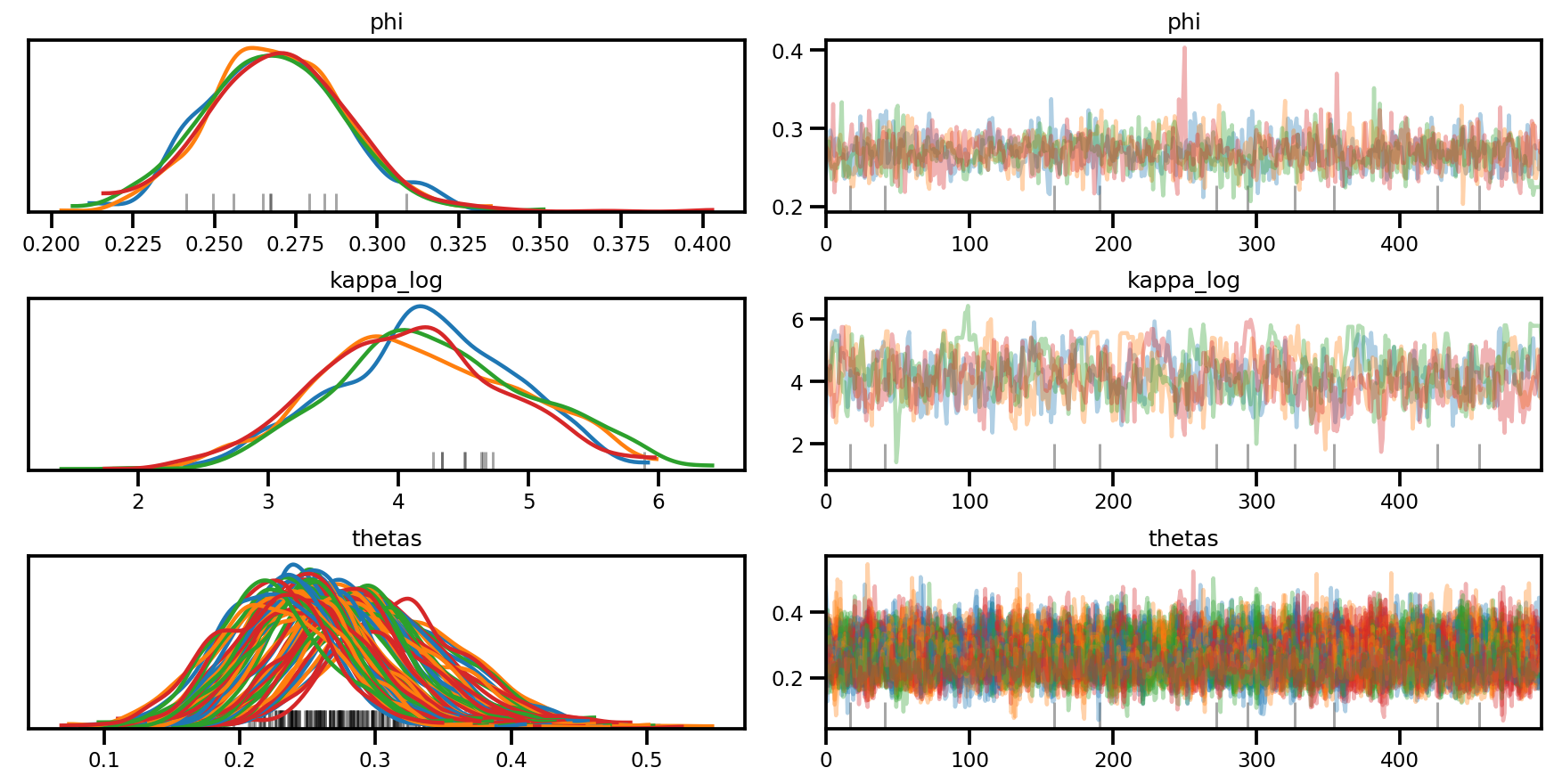
az.plot_forest(az_trace,
var_names=['thetas'],
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 8));
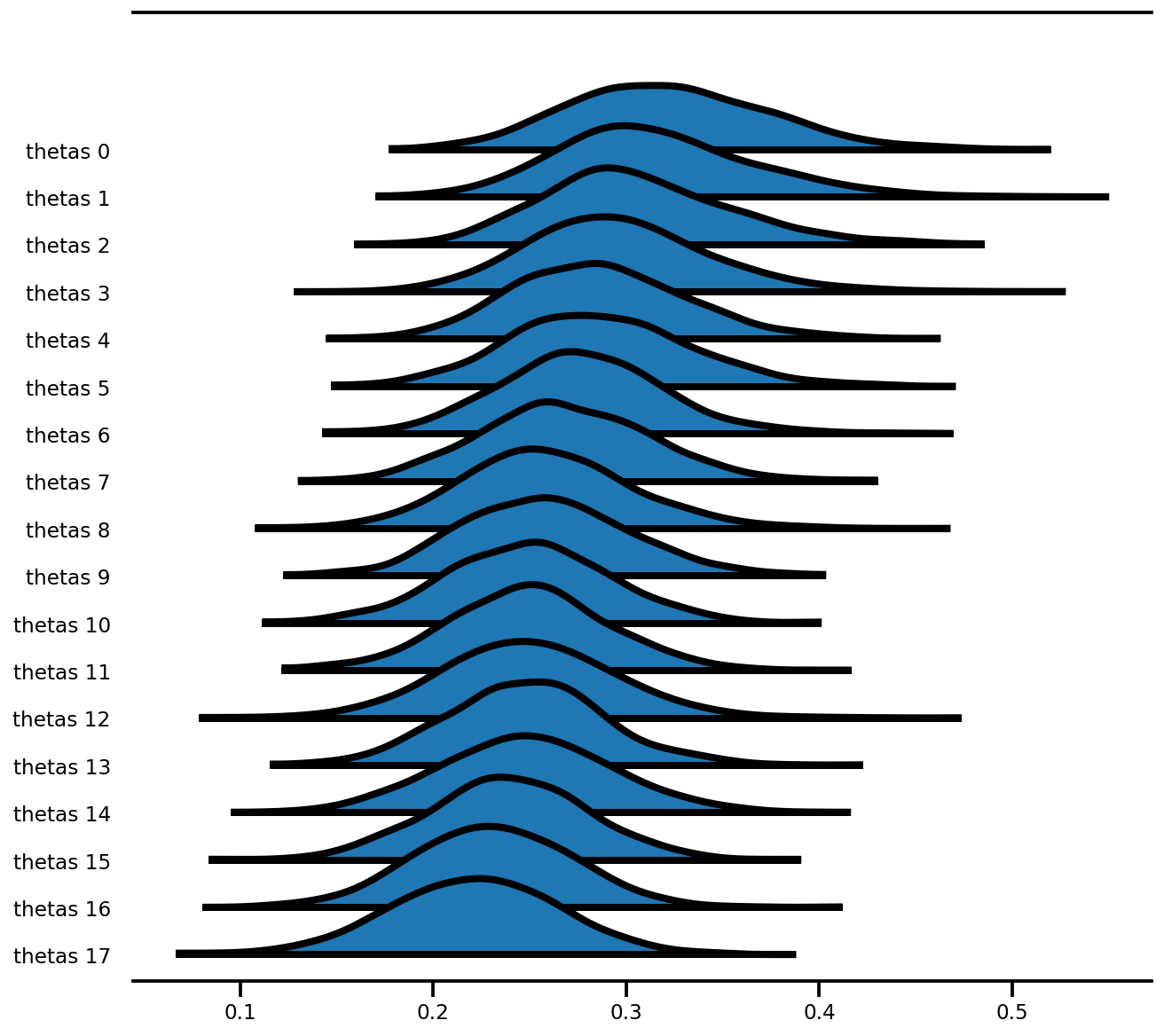
Model efek campuran (Radon)
Model terakhir dalam doc PyMC3: A Primer pada Metode Bayesian untuk Multilevel Modeling
Beberapa perubahan sebelumnya (skala lebih kecil dll)
Muat data mentah dan bersihkan
srrs2 = pd.read_csv('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/srrs2.dat')
srrs2.columns = srrs2.columns.map(str.strip)
srrs_mn = srrs2[srrs2.state=='MN'].copy()
srrs_mn['fips'] = srrs_mn.stfips*1000 + srrs_mn.cntyfips
cty = pd.read_csv('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/cty.dat')
cty_mn = cty[cty.st=='MN'].copy()
cty_mn[ 'fips'] = 1000*cty_mn.stfips + cty_mn.ctfips
srrs_mn = srrs_mn.merge(cty_mn[['fips', 'Uppm']], on='fips')
srrs_mn = srrs_mn.drop_duplicates(subset='idnum')
u = np.log(srrs_mn.Uppm)
n = len(srrs_mn)
srrs_mn.county = srrs_mn.county.map(str.strip)
mn_counties = srrs_mn.county.unique()
counties = len(mn_counties)
county_lookup = dict(zip(mn_counties, range(len(mn_counties))))
county = srrs_mn['county_code'] = srrs_mn.county.replace(county_lookup).values
radon = srrs_mn.activity
srrs_mn['log_radon'] = log_radon = np.log(radon + 0.1).values
floor_measure = srrs_mn.floor.values.astype('float')
# Create new variable for mean of floor across counties
xbar = srrs_mn.groupby('county')['floor'].mean().rename(county_lookup).values
Untuk model dengan transformasi kompleks, menerapkannya dalam gaya fungsional akan membuat penulisan dan pengujian menjadi lebih mudah. Selain itu, ini membuat fungsi log_prob yang dihasilkan secara terprogram yang dikondisikan pada (mini-batch) data yang dimasukkan menjadi lebih mudah:
def affine(u_val, x_county, county, floor, gamma, eps, b):
"""Linear equation of the coefficients and the covariates, with broadcasting."""
return (tf.transpose((gamma[..., 0]
+ gamma[..., 1]*u_val[:, None]
+ gamma[..., 2]*x_county[:, None]))
+ tf.gather(eps, county, axis=-1)
+ b*floor)
def gen_radon_model(u_val, x_county, county, floor,
mu0=tf.zeros([], dtype, name='mu0')):
"""Creates a joint distribution representing our generative process."""
return tfd.JointDistributionSequential([
# sigma_a
tfd.HalfCauchy(loc=mu0, scale=5.),
# eps
lambda sigma_a: tfd.Sample(
tfd.Normal(loc=mu0, scale=sigma_a), sample_shape=counties),
# gamma
tfd.Sample(tfd.Normal(loc=mu0, scale=100.), sample_shape=3),
# b
tfd.Sample(tfd.Normal(loc=mu0, scale=100.), sample_shape=1),
# sigma_y
tfd.Sample(tfd.HalfCauchy(loc=mu0, scale=5.), sample_shape=1),
# likelihood
lambda sigma_y, b, gamma, eps: tfd.Independent(
tfd.Normal(
loc=affine(u_val, x_county, county, floor, gamma, eps, b),
scale=sigma_y
),
reinterpreted_batch_ndims=1
),
])
contextual_effect2 = gen_radon_model(
u.values, xbar[county], county, floor_measure)
@tf.function(autograph=False)
def unnormalized_posterior_log_prob(sigma_a, gamma, eps, b, sigma_y):
"""Computes `joint_log_prob` pinned at `log_radon`."""
return contextual_effect2.log_prob(
[sigma_a, gamma, eps, b, sigma_y, log_radon])
assert [4] == unnormalized_posterior_log_prob(
*contextual_effect2.sample(4)[:-1]).shape
samples = contextual_effect2.sample(4)
pprint([s.shape for s in samples])
[TensorShape([4]), TensorShape([4, 85]), TensorShape([4, 3]), TensorShape([4, 1]), TensorShape([4, 1]), TensorShape([4, 919])]
contextual_effect2.log_prob_parts(list(samples)[:-1] + [log_radon])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-3.95681828, -2.45693443, -2.53310078, -4.7717536 ])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-340.65975204, -217.11139018, -246.50498667, -369.79687704])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-20.49822449, -20.38052557, -18.63843525, -17.83096972])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-5.94765605, -5.91460848, -6.66169402, -5.53894593])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-2.10293999, -4.34186631, -2.10744955, -3.016717 ])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=
array([-29022322.1413861 , -114422.36893361, -8708500.81752865,
-35061.92497235])>]
Inferensi Variasi
Salah satu fitur yang sangat kuat dari JointDistribution* adalah bahwa Anda dapat menghasilkan sebuah pendekatan mudah untuk VI. Misalnya, untuk melakukan ADVI meanfield, Anda cukup memeriksa grafik dan mengganti semua distribusi yang tidak teramati dengan distribusi Normal.
meanfield ADVI
Anda juga dapat menggunakan fitur experimential di tensorflow_probability / python / eksperimental / vi untuk membangun pendekatan variasional, yang pada dasarnya logika yang sama digunakan di bawah (yaitu, menggunakan JointDistribution untuk membangun pendekatan), tetapi dengan output pendekatan dalam ruang asli bukan ruang tak terbatas.
from tensorflow_probability.python.mcmc.transformed_kernel import (
make_transform_fn, make_transformed_log_prob)
# Wrap logp so that all parameters are in the Real domain
# copied and edited from tensorflow_probability/python/mcmc/transformed_kernel.py
unconstraining_bijectors = [
tfb.Exp(),
tfb.Identity(),
tfb.Identity(),
tfb.Identity(),
tfb.Exp()
]
unnormalized_log_prob = lambda *x: contextual_effect2.log_prob(x + (log_radon,))
contextual_effect_posterior = make_transformed_log_prob(
unnormalized_log_prob,
unconstraining_bijectors,
direction='forward',
# TODO(b/72831017): Disable caching until gradient linkage
# generally works.
enable_bijector_caching=False)
# debug
if True:
# Check the two versions of log_prob - they should be different given the Jacobian
rv_samples = contextual_effect2.sample(4)
_inverse_transform = make_transform_fn(unconstraining_bijectors, 'inverse')
_forward_transform = make_transform_fn(unconstraining_bijectors, 'forward')
pprint([
unnormalized_log_prob(*rv_samples[:-1]),
contextual_effect_posterior(*_inverse_transform(rv_samples[:-1])),
unnormalized_log_prob(
*_forward_transform(
tf.zeros_like(a, dtype=dtype) for a in rv_samples[:-1])
),
contextual_effect_posterior(
*[tf.zeros_like(a, dtype=dtype) for a in rv_samples[:-1]]
),
])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.73354969e+04, -5.51622488e+04, -2.77754609e+08, -1.09065161e+07])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.73331358e+04, -5.51582029e+04, -2.77754602e+08, -1.09065134e+07])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1992.10420767, -1992.10420767, -1992.10420767, -1992.10420767])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1992.10420767, -1992.10420767, -1992.10420767, -1992.10420767])>]
# Build meanfield ADVI for a jointdistribution
# Inspect the input jointdistribution and replace the list of distribution with
# a list of Normal distribution, each with the same shape.
def build_meanfield_advi(jd_list, observed_node=-1):
"""
The inputted jointdistribution needs to be a batch version
"""
# Sample to get a list of Tensors
list_of_values = jd_list.sample(1) # <== sample([]) might not work
# Remove the observed node
list_of_values.pop(observed_node)
# Iterate the list of Tensor to a build a list of Normal distribution (i.e.,
# the Variational posterior)
distlist = []
for i, value in enumerate(list_of_values):
dtype = value.dtype
rv_shape = value[0].shape
loc = tf.Variable(
tf.random.normal(rv_shape, dtype=dtype),
name='meanfield_%s_mu' % i,
dtype=dtype)
scale = tfp.util.TransformedVariable(
tf.fill(rv_shape, value=tf.constant(0.02, dtype)),
tfb.Softplus(),
name='meanfield_%s_scale' % i,
)
approx_node = tfd.Normal(loc=loc, scale=scale)
if loc.shape == ():
distlist.append(approx_node)
else:
distlist.append(
# TODO: make the reinterpreted_batch_ndims more flexible (for
# minibatch etc)
tfd.Independent(approx_node, reinterpreted_batch_ndims=1)
)
# pass list to JointDistribution to initiate the meanfield advi
meanfield_advi = tfd.JointDistributionSequential(distlist)
return meanfield_advi
advi = build_meanfield_advi(contextual_effect2, observed_node=-1)
# Check the logp and logq
advi_samples = advi.sample(4)
pprint([
advi.log_prob(advi_samples),
contextual_effect_posterior(*advi_samples)
])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([231.26836839, 229.40755095, 227.10287879, 224.05914594])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-10615.93542431, -11743.21420129, -10376.26732337, -11338.00600103])>]
opt = tf.optimizers.Adam(learning_rate=.1)
@tf.function(experimental_compile=True)
def run_approximation():
loss_ = tfp.vi.fit_surrogate_posterior(
contextual_effect_posterior,
surrogate_posterior=advi,
optimizer=opt,
sample_size=10,
num_steps=300)
return loss_
loss_ = run_approximation()
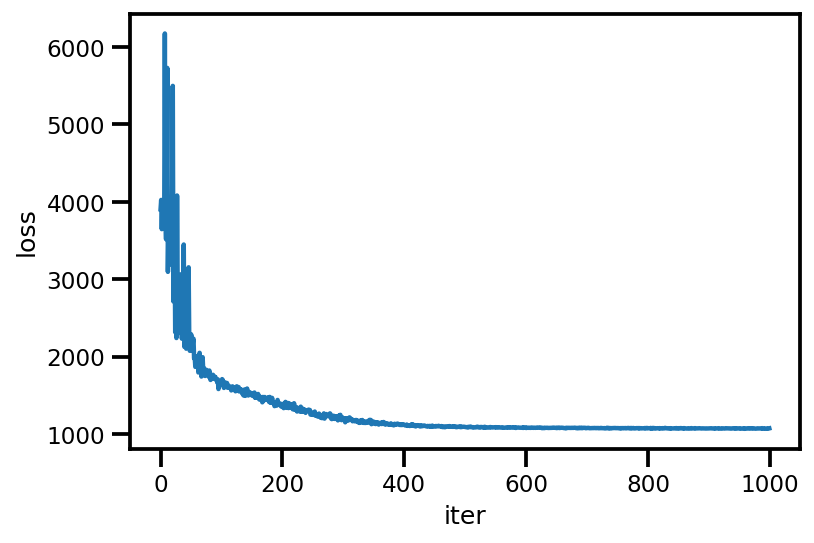
plt.plot(loss_);
plt.xlabel('iter');
plt.ylabel('loss');
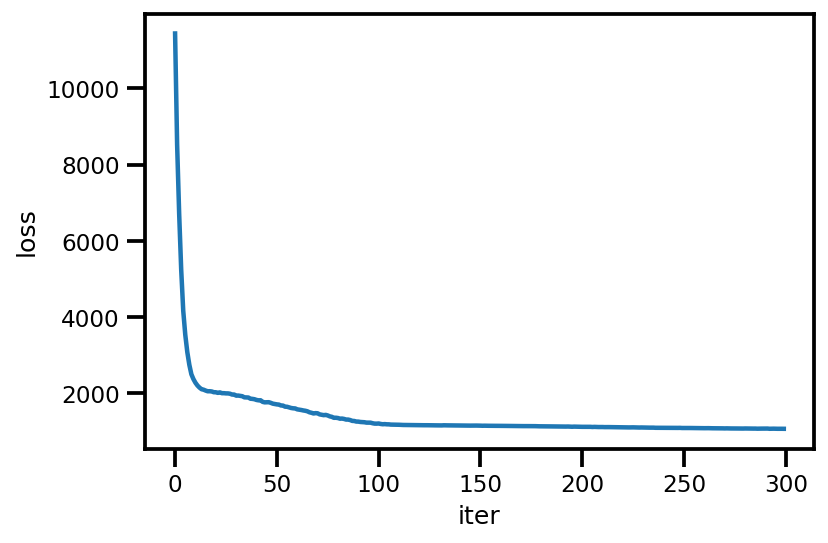
graph_info = contextual_effect2.resolve_graph()
approx_param = dict()
free_param = advi.trainable_variables
for i, (rvname, param) in enumerate(graph_info[:-1]):
approx_param[rvname] = {"mu": free_param[i*2].numpy(),
"sd": free_param[i*2+1].numpy()}
approx_param.keys()
dict_keys(['sigma_a', 'eps', 'gamma', 'b', 'sigma_y'])
approx_param['gamma']
{'mu': array([1.28145814, 0.70365287, 1.02689857]),
'sd': array([-3.6604972 , -2.68153218, -2.04176524])}
a_means = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county])
_, index = np.unique(county, return_index=True)
plt.scatter(u.values[index], a_means[index], color='g')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,
approx_param['gamma']['mu'][0]+approx_param['gamma']['mu'][1]*xvals,
'k--')
plt.xlim(-1, 0.8)
plt.xlabel('County-level uranium');
plt.ylabel('Intercept estimate');
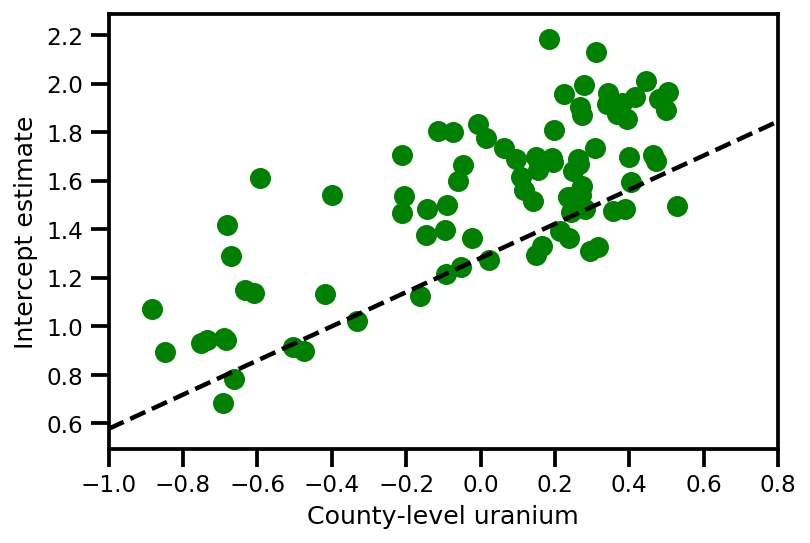
y_est = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county]
+ approx_param['b']['mu']*floor_measure)
_, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(county, log_radon, 'o', alpha=.25, label='observed')
ax.plot(county, y_est, '-o', lw=2, alpha=.5, label='y_hat')
ax.set_xlim(-1, county.max()+1)
plt.legend(loc='lower right')
ax.set_xlabel('County #')
ax.set_ylabel('log(Uranium) level');
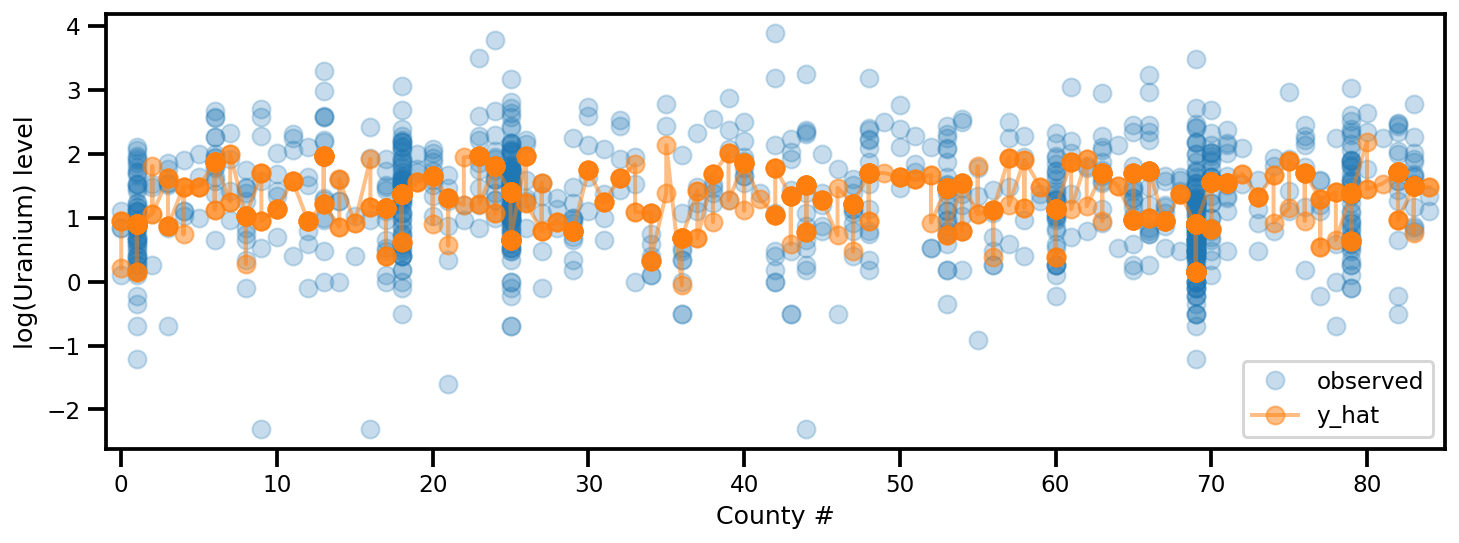
ADVI Peringkat Penuh
Untuk ADVI peringkat penuh, kami ingin memperkirakan posterior dengan Gaussian multivariat.
USE_FULLRANK = True
*prior_tensors, _ = contextual_effect2.sample()
mapper = Mapper(prior_tensors,
[tfb.Identity() for _ in prior_tensors],
contextual_effect2.event_shape[:-1])
rv_shape = ps.shape(mapper.flatten_and_concat(mapper.list_of_tensors))
init_val = tf.random.normal(rv_shape, dtype=dtype)
loc = tf.Variable(init_val, name='loc', dtype=dtype)
if USE_FULLRANK:
# cov_param = tfp.util.TransformedVariable(
# 10. * tf.eye(rv_shape[0], dtype=dtype),
# tfb.FillScaleTriL(),
# name='cov_param'
# )
FillScaleTriL = tfb.FillScaleTriL(
diag_bijector=tfb.Chain([
tfb.Shift(tf.cast(.01, dtype)),
tfb.Softplus(),
tfb.Shift(tf.cast(np.log(np.expm1(1.)), dtype))]),
diag_shift=None)
cov_param = tfp.util.TransformedVariable(
.02 * tf.eye(rv_shape[0], dtype=dtype),
FillScaleTriL,
name='cov_param')
advi_approx = tfd.MultivariateNormalTriL(
loc=loc, scale_tril=cov_param)
else:
# An alternative way to build meanfield ADVI.
cov_param = tfp.util.TransformedVariable(
.02 * tf.ones(rv_shape, dtype=dtype),
tfb.Softplus(),
name='cov_param'
)
advi_approx = tfd.MultivariateNormalDiag(
loc=loc, scale_diag=cov_param)
contextual_effect_posterior2 = lambda x: contextual_effect_posterior(
*mapper.split_and_reshape(x)
)
# Check the logp and logq
advi_samples = advi_approx.sample(7)
pprint([
advi_approx.log_prob(advi_samples),
contextual_effect_posterior2(advi_samples)
])
[<tf.Tensor: shape=(7,), dtype=float64, numpy=
array([238.81841799, 217.71022639, 234.57207103, 230.0643819 ,
243.73140943, 226.80149702, 232.85184209])>,
<tf.Tensor: shape=(7,), dtype=float64, numpy=
array([-3638.93663169, -3664.25879314, -3577.69371677, -3696.25705312,
-3689.12130489, -3777.53698383, -3659.4982734 ])>]
learning_rate = tf.optimizers.schedules.ExponentialDecay(
initial_learning_rate=1e-2,
decay_steps=10,
decay_rate=0.99,
staircase=True)
opt = tf.optimizers.Adam(learning_rate=learning_rate)
@tf.function(experimental_compile=True)
def run_approximation():
loss_ = tfp.vi.fit_surrogate_posterior(
contextual_effect_posterior2,
surrogate_posterior=advi_approx,
optimizer=opt,
sample_size=10,
num_steps=1000)
return loss_
loss_ = run_approximation()
plt.plot(loss_);
plt.xlabel('iter');
plt.ylabel('loss');
# debug
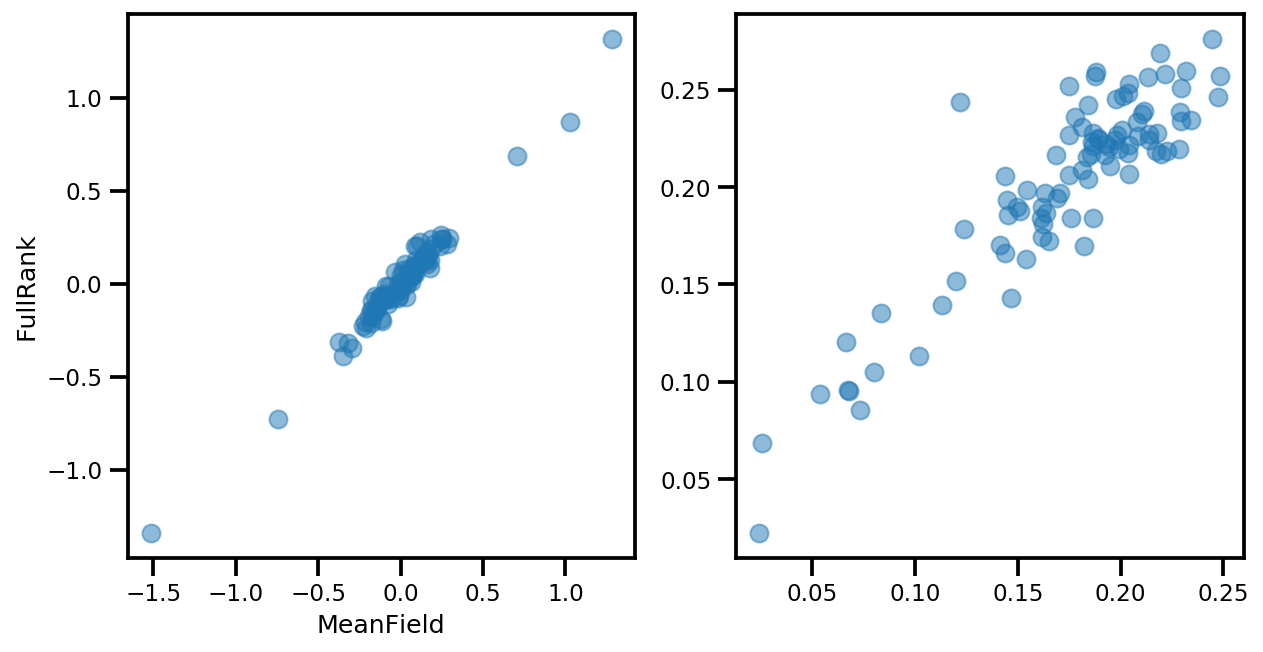
if True:
_, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(mapper.flatten_and_concat(advi.mean()), advi_approx.mean(), 'o', alpha=.5)
ax[1].plot(mapper.flatten_and_concat(advi.stddev()), advi_approx.stddev(), 'o', alpha=.5)
ax[0].set_xlabel('MeanField')
ax[0].set_ylabel('FullRank')
graph_info = contextual_effect2.resolve_graph()
approx_param = dict()
free_param_mean = mapper.split_and_reshape(advi_approx.mean())
free_param_std = mapper.split_and_reshape(advi_approx.stddev())
for i, (rvname, param) in enumerate(graph_info[:-1]):
approx_param[rvname] = {"mu": free_param_mean[i].numpy(),
"cov_info": free_param_std[i].numpy()}
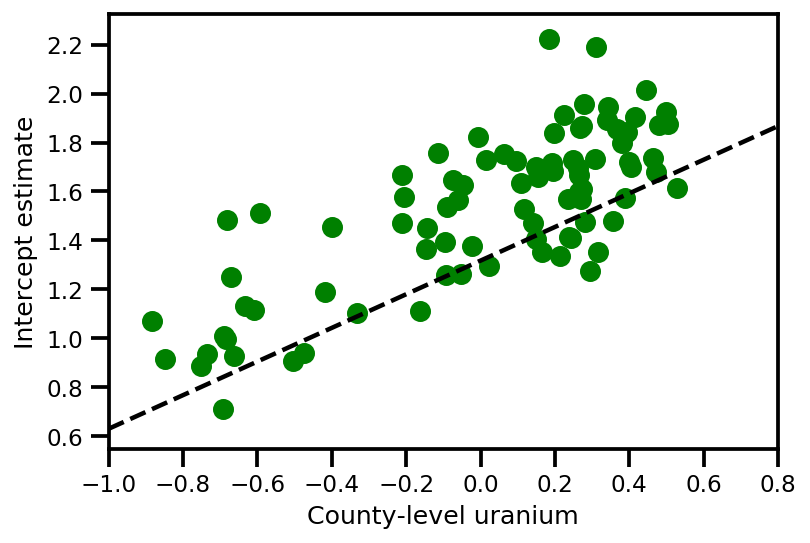
a_means = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county])
_, index = np.unique(county, return_index=True)
plt.scatter(u.values[index], a_means[index], color='g')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,
approx_param['gamma']['mu'][0]+approx_param['gamma']['mu'][1]*xvals,
'k--')
plt.xlim(-1, 0.8)
plt.xlabel('County-level uranium');
plt.ylabel('Intercept estimate');
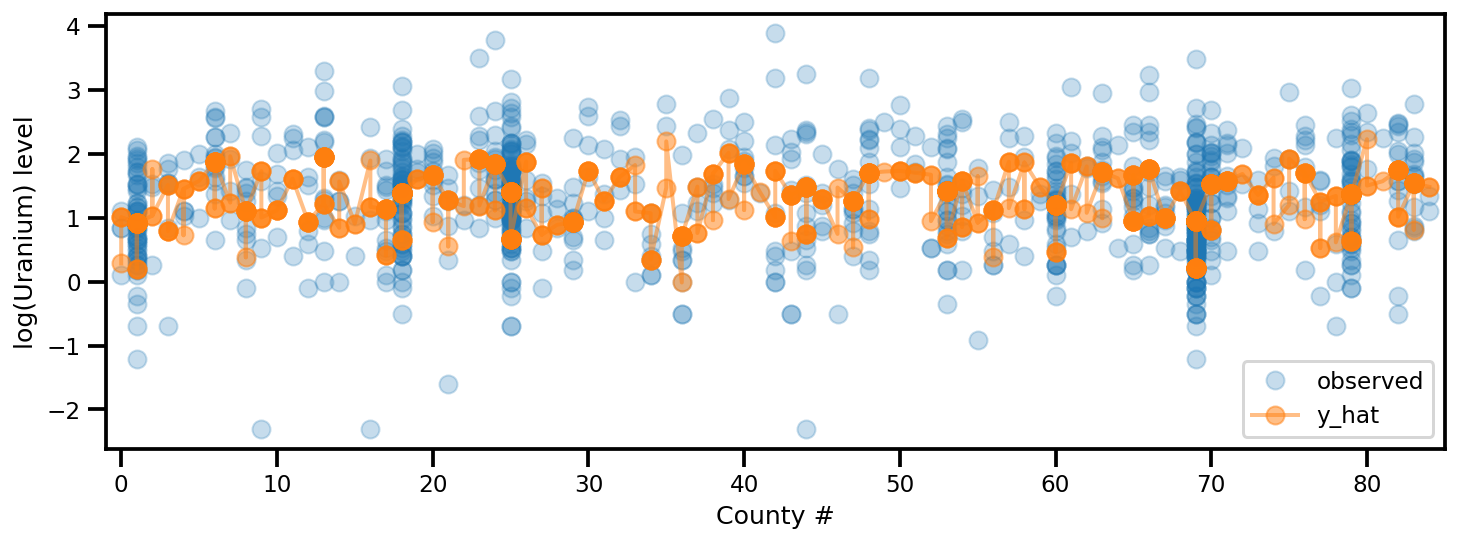
y_est = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county]
+ approx_param['b']['mu']*floor_measure)
_, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(county, log_radon, 'o', alpha=.25, label='observed')
ax.plot(county, y_est, '-o', lw=2, alpha=.5, label='y_hat')
ax.set_xlim(-1, county.max()+1)
plt.legend(loc='lower right')
ax.set_xlabel('County #')
ax.set_ylabel('log(Uranium) level');
Model Campuran Beta-Bernoulli
Model campuran di mana beberapa pengulas melabeli beberapa item, dengan label laten yang tidak diketahui (benar).
dtype = tf.float32
n = 50000 # number of examples reviewed
p_bad_ = 0.1 # fraction of bad events
m = 5 # number of reviewers for each example
rcl_ = .35 + np.random.rand(m)/10
prc_ = .65 + np.random.rand(m)/10
# PARAMETER TRANSFORMATION
tpr = rcl_
fpr = p_bad_*tpr*(1./prc_-1.)/(1.-p_bad_)
tnr = 1 - fpr
# broadcast to m reviewer.
batch_prob = np.asarray([tpr, fpr]).T
mixture = tfd.Mixture(
tfd.Categorical(
probs=[p_bad_, 1-p_bad_]),
[
tfd.Independent(tfd.Bernoulli(probs=tpr), 1),
tfd.Independent(tfd.Bernoulli(probs=fpr), 1),
])
# Generate reviewer response
X_tf = mixture.sample([n])
# run once to always use the same array as input
# so we can compare the estimation from different
# inference method.
X_np = X_tf.numpy()
# batched Mixture model
mdl_mixture = tfd.JointDistributionSequential([
tfd.Sample(tfd.Beta(5., 2.), m),
tfd.Sample(tfd.Beta(2., 2.), m),
tfd.Sample(tfd.Beta(1., 10), 1),
lambda p_bad, rcl, prc: tfd.Sample(
tfd.Mixture(
tfd.Categorical(
probs=tf.concat([p_bad, 1.-p_bad], -1)),
[
tfd.Independent(tfd.Bernoulli(
probs=rcl), 1),
tfd.Independent(tfd.Bernoulli(
probs=p_bad*rcl*(1./prc-1.)/(1.-p_bad)), 1)
]
), (n, )),
])
mdl_mixture.resolve_graph()
(('prc', ()), ('rcl', ()), ('p_bad', ()), ('x', ('p_bad', 'rcl', 'prc')))
prc, rcl, p_bad, x = mdl_mixture.sample(4)
x.shape
TensorShape([4, 50000, 5])
mdl_mixture.log_prob_parts([prc, rcl, p_bad, X_np[np.newaxis, ...]])
[<tf.Tensor: shape=(4,), dtype=float32, numpy=array([1.4828572, 2.957961 , 2.9355168, 2.6116824], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.14646745, 1.3308513 , 1.1205603 , 0.5441705 ], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([1.3733709, 1.8020535, 2.1865845, 1.5701319], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([-54326.664, -52683.93 , -64407.67 , -55007.895], dtype=float32)>]
Inferensi (KACANG)
nchain = 10
prc, rcl, p_bad, _ = mdl_mixture.sample(nchain)
initial_chain_state = [prc, rcl, p_bad]
# Since MCMC operates over unconstrained space, we need to transform the
# samples so they live in real-space.
unconstraining_bijectors = [
tfb.Sigmoid(), # Maps R to [0, 1].
tfb.Sigmoid(), # Maps R to [0, 1].
tfb.Sigmoid(), # Maps R to [0, 1].
]
step_size = [tf.cast(i, dtype=dtype) for i in [1e-3, 1e-3, 1e-3]]
X_expanded = X_np[np.newaxis, ...]
target_log_prob_fn = lambda *x: mdl_mixture.log_prob(x + (X_expanded, ))
samples, sampler_stat = run_chain(
initial_chain_state, step_size, target_log_prob_fn,
unconstraining_bijectors, burnin=100)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
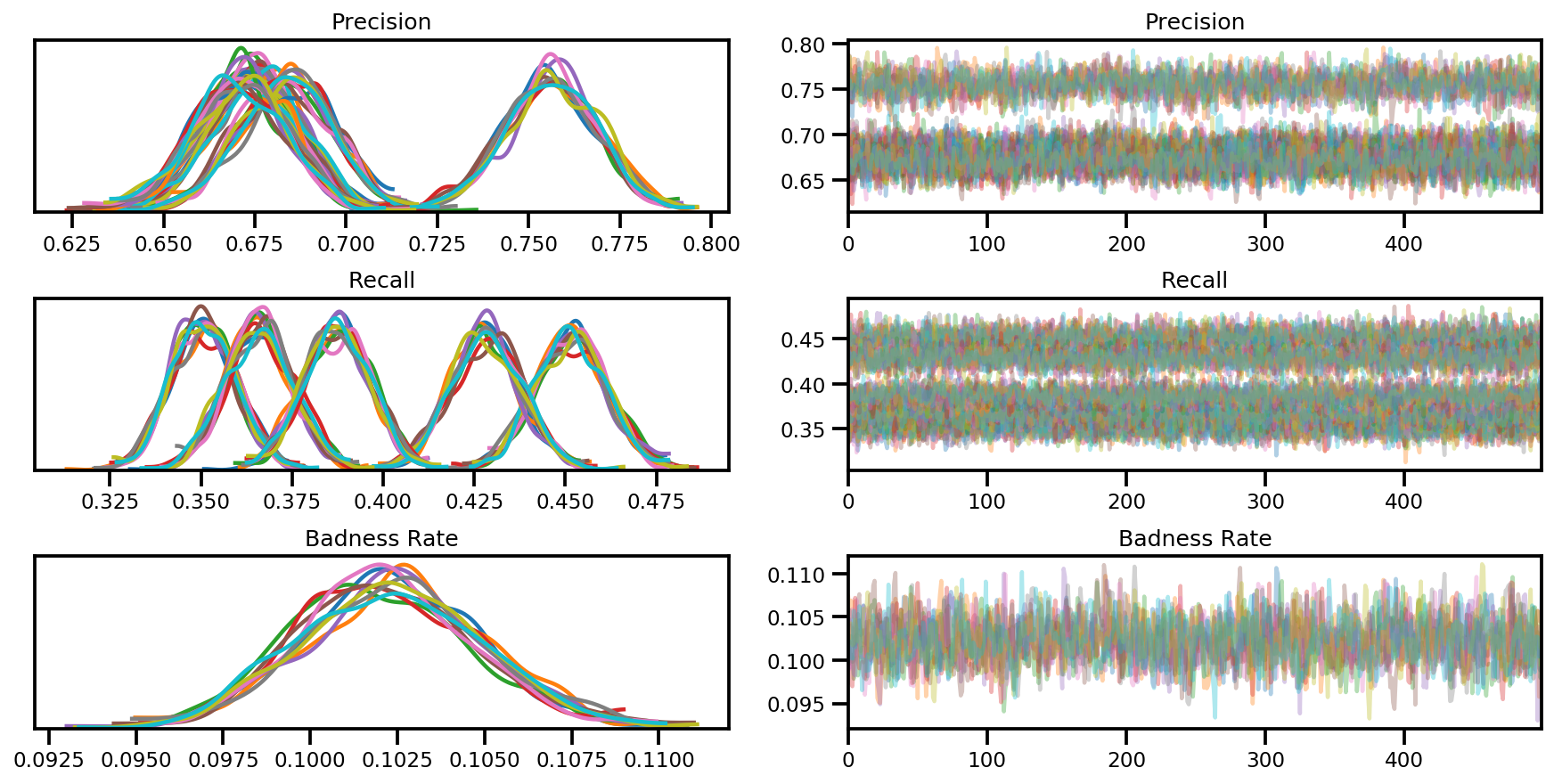
var_name = ['Precision', 'Recall', 'Badness Rate']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
axes = az.plot_trace(az_trace, compact=True);