TensorFlow kembali hadir di Google I/O pada 14 Mei! Daftar sekarang

Halaman ini diterjemahkan oleh Cloud Translation API.

Diferensiasi otomatis tingkat lanjut

Lihat di TensorFlow.org

Jalankan di Google Colab

Lihat sumber di GitHub

Unduh buku catatan

Panduan Pengenalan gradien dan diferensiasi otomatis mencakup semua yang diperlukan untuk menghitung gradien di TensorFlow. Panduan ini berfokus pada fitur tf.GradientTape API yang lebih dalam dan kurang umum.

Mempersiapkan

import tensorflow as tf

import matplotlib as mpl
import matplotlib.pyplot as plt

mpl.rcParams['figure.figsize'] = (8, 6)

Mengontrol perekaman gradien

Dalam panduan diferensiasi otomatis , Anda melihat cara mengontrol variabel dan tensor mana yang diawasi oleh pita sambil membangun perhitungan gradien.

Rekaman itu juga memiliki metode untuk memanipulasi rekaman.

Berhenti merekam

Jika Anda ingin berhenti merekam gradien, Anda dapat menggunakan tf.GradientTape.stop_recording untuk menangguhkan perekaman sementara.

Ini mungkin berguna untuk mengurangi overhead jika Anda tidak ingin membedakan operasi yang rumit di tengah model Anda. Ini dapat mencakup penghitungan metrik atau hasil antara:

x = tf.Variable(2.0)
y = tf.Variable(3.0)

with tf.GradientTape() as t:
  x_sq = x * x
  with t.stop_recording():
    y_sq = y * y
  z = x_sq + y_sq

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Setel ulang/mulai merekam dari awal

Jika Anda ingin memulai kembali seluruhnya, gunakan tf.GradientTape.reset . Cukup keluar dari blok pita gradien dan memulai ulang biasanya lebih mudah dibaca, tetapi Anda dapat menggunakan metode reset saat keluar dari blok pita sulit atau tidak mungkin.

x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True

with tf.GradientTape() as t:
  y_sq = y * y
  if reset:
    # Throw out all the tape recorded so far.
    t.reset()
  z = x * x + y_sq

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Hentikan aliran gradien dengan presisi

Berbeda dengan kontrol pita global di atas, fungsi tf.stop_gradient jauh lebih presisi. Ini dapat digunakan untuk menghentikan gradien agar tidak mengalir di sepanjang jalur tertentu, tanpa memerlukan akses ke pita itu sendiri:

x = tf.Variable(2.0)
y = tf.Variable(3.0)

with tf.GradientTape() as t:
  y_sq = y**2
  z = x**2 + tf.stop_gradient(y_sq)

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Gradien khusus

Dalam beberapa kasus, Anda mungkin ingin mengontrol dengan tepat bagaimana gradien dihitung daripada menggunakan default. Situasi ini meliputi:

Tidak ada gradien yang ditentukan untuk operasi baru yang Anda tulis.
Perhitungan default secara numerik tidak stabil.
Anda ingin men-cache komputasi yang mahal dari forward pass.
Anda ingin mengubah nilai (misalnya, menggunakan tf.clip_by_value atau tf.math.round ) tanpa mengubah gradien.

Untuk kasus pertama, untuk menulis operasi baru, Anda dapat menggunakan tf.RegisterGradient untuk menyiapkan operasi Anda sendiri (lihat dokumen API untuk detailnya). (Perhatikan bahwa registri gradien bersifat global, jadi ubahlah dengan hati-hati.)

Untuk tiga kasus terakhir, Anda dapat menggunakan tf.custom_gradient .

Berikut adalah contoh yang menerapkan tf.clip_by_norm ke gradien perantara:

# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
  def backward(dy):
    return tf.clip_by_norm(dy, 0.5)
  return y, backward

v = tf.Variable(2.0)
with tf.GradientTape() as t:
  output = clip_gradients(v * v)
print(t.gradient(output, v))  # calls "backward", which clips 4 to 2

tf.Tensor(2.0, shape=(), dtype=float32)

Lihat dokumen API dekorator tf.custom_gradient untuk detail selengkapnya.

Gradien khusus di SavedModel

Gradien kustom dapat disimpan ke SavedModel dengan menggunakan opsi tf.saved_model.SaveOptions(experimental_custom_gradients=True) .

Untuk disimpan ke dalam SavedModel, fungsi gradien harus dapat dilacak (untuk mempelajari lebih lanjut, lihat Panduan kinerja yang lebih baik dengan tf.function ).

class MyModule(tf.Module):

  @tf.function(input_signature=[tf.TensorSpec(None)])
  def call_custom_grad(self, x):
    return clip_gradients(x)

model = MyModule()

tf.saved_model.save(
    model,
    'saved_model',
    options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))

# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
  output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))

INFO:tensorflow:Assets written to: saved_model/assets
tf.Tensor(2.0, shape=(), dtype=float32)

Catatan tentang contoh di atas: Jika Anda mencoba mengganti kode di atas dengan tf.saved_model.SaveOptions(experimental_custom_gradients=False) , gradien akan tetap menghasilkan hasil yang sama saat memuat. Alasannya adalah registri gradien masih berisi gradien khusus yang digunakan dalam fungsi call_custom_op . Namun, jika Anda me-restart runtime setelah menyimpan tanpa gradien kustom, menjalankan model yang dimuat di bawah tf.GradientTape akan memunculkan kesalahan: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .

Beberapa kaset

Beberapa kaset berinteraksi dengan mulus.

Sebagai contoh, di sini setiap kaset melihat set tensor yang berbeda:

x0 = tf.constant(0.0)
x1 = tf.constant(0.0)

with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
  tape0.watch(x0)
  tape1.watch(x1)

  y0 = tf.math.sin(x0)
  y1 = tf.nn.sigmoid(x1)

  y = y0 + y1

  ys = tf.reduce_sum(y)

tape0.gradient(ys, x0).numpy()   # cos(x) => 1.0

1.0

tape1.gradient(ys, x1).numpy()   # sigmoid(x1)*(1-sigmoid(x1)) => 0.25

0.25

Gradien tingkat tinggi

Operasi di dalam manajer konteks tf.GradientTape direkam untuk diferensiasi otomatis. Jika gradien dihitung dalam konteks itu, maka perhitungan gradien juga dicatat. Akibatnya, API yang sama persis juga berfungsi untuk gradien tingkat tinggi.

Sebagai contoh:

x = tf.Variable(1.0)  # Create a Tensorflow variable initialized to 1.0

with tf.GradientTape() as t2:
  with tf.GradientTape() as t1:
    y = x * x * x

  # Compute the gradient inside the outer `t2` context manager
  # which means the gradient computation is differentiable as well.
  dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)

print('dy_dx:', dy_dx.numpy())  # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy())  # 6 * x => 6.0

dy_dx: 3.0
d2y_dx2: 6.0

Meskipun hal itu memberi Anda turunan kedua dari fungsi skalar , pola ini tidak digeneralisasi untuk menghasilkan matriks Hessian, karena tf.GradientTape.gradient hanya menghitung gradien skalar. Untuk membuat matriks Hessian , lihat contoh Hessian di bawah bagian Jacobian .

"Panggilan bersarang ke tf.GradientTape.gradient " adalah pola yang baik saat Anda menghitung skalar dari gradien, lalu skalar yang dihasilkan bertindak sebagai sumber untuk penghitungan gradien kedua, seperti dalam contoh berikut.

Contoh: Regularisasi gradien masukan

Banyak model rentan terhadap "contoh permusuhan". Kumpulan teknik ini memodifikasi input model untuk membingungkan output model. Implementasi paling sederhana—seperti contoh Adversarial menggunakan serangan Fast Gradient Signed Method —mengambil satu langkah di sepanjang gradien output sehubungan dengan input; "gradien masukan".

Salah satu teknik untuk meningkatkan ketahanan terhadap contoh permusuhan adalah regularisasi gradien input (Finlay & Oberman, 2019), yang berupaya meminimalkan besarnya gradien input. Jika gradien input kecil, maka perubahan output juga harus kecil.

Di bawah ini adalah implementasi naif dari regularisasi gradien input. Implementasinya adalah:

Hitung gradien output terhadap input menggunakan pita bagian dalam.
Hitung besarnya gradien input tersebut.
Hitung gradien besarnya itu terhadap model.

x = tf.random.normal([7, 5])

layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)

with tf.GradientTape() as t2:
  # The inner tape only takes the gradient with respect to the input,
  # not the variables.
  with tf.GradientTape(watch_accessed_variables=False) as t1:
    t1.watch(x)
    y = layer(x)
    out = tf.reduce_sum(layer(x)**2)
  # 1. Calculate the input gradient.
  g1 = t1.gradient(out, x)
  # 2. Calculate the magnitude of the input gradient.
  g1_mag = tf.norm(g1)

# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)

[var.shape for var in dg1_mag]

[TensorShape([5, 10]), TensorShape([10])]

Jacobian

Semua contoh sebelumnya mengambil gradien target skalar sehubungan dengan beberapa tensor sumber.

Matriks Jacobian mewakili gradien dari fungsi bernilai vektor. Setiap baris berisi gradien dari salah satu elemen vektor.

Metode tf.GradientTape.jacobian memungkinkan Anda menghitung matriks Jacobian secara efisien.

Perhatikan bahwa:

Seperti gradient : Argumen sources dapat berupa tensor atau wadah tensor.
Tidak seperti gradient : Tensor target harus berupa tensor tunggal.

sumber skalar

Sebagai contoh pertama, berikut adalah Jacobian dari target vektor sehubungan dengan sumber skalar.

x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)

with tf.GradientTape() as tape:
  y = tf.nn.sigmoid(x+delta)

dy_dx = tape.jacobian(y, delta)

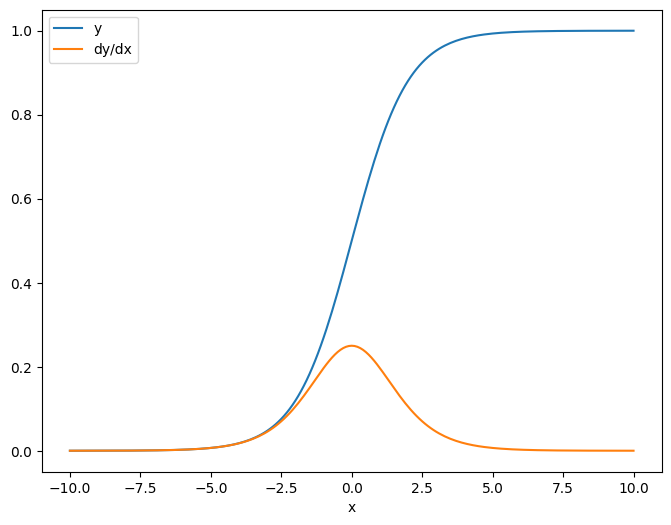
Ketika Anda mengambil Jacobian sehubungan dengan skalar, hasilnya memiliki bentuk target , dan memberikan gradien dari setiap elemen sehubungan dengan sumbernya:

print(y.shape)
print(dy_dx.shape)

(201,)
(201,)

plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')

png

sumber tensor

Baik inputnya skalar atau tensor, tf.GradientTape.jacobian secara efisien menghitung gradien setiap elemen sumber sehubungan dengan setiap elemen target.

Sebagai contoh, output dari layer ini memiliki bentuk (10, 7) :

x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)

with tf.GradientTape(persistent=True) as tape:
  y = layer(x)

y.shape

TensorShape([7, 10])

Dan bentuk kernel layer adalah (5, 10) :

layer.kernel.shape

TensorShape([5, 10])

Bentuk Jacobian dari output sehubungan dengan kernel adalah dua bentuk yang digabungkan bersama:

j = tape.jacobian(y, layer.kernel)
j.shape

TensorShape([7, 10, 5, 10])

Jika Anda menjumlahkan dimensi target, Anda memiliki gradien jumlah yang akan dihitung oleh tf.GradientTape.gradient :

g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)

j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)

g.shape: (5, 10)
delta: 2.3841858e-07

Contoh: Hessian

Meskipun tf.GradientTape tidak memberikan metode eksplisit untuk membangun matriks Hessian , mungkin untuk membuatnya menggunakan metode tf.GradientTape.jacobian .

x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)

with tf.GradientTape() as t2:
  with tf.GradientTape() as t1:
    x = layer1(x)
    x = layer2(x)
    loss = tf.reduce_mean(x**2)

  g = t1.gradient(loss, layer1.kernel)

h = t2.jacobian(g, layer1.kernel)

print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')

layer.kernel.shape: (5, 8)
h.shape: (5, 8, 5, 8)

Untuk menggunakan Hessian ini untuk langkah metode Newton , pertama-tama Anda akan meratakan sumbunya menjadi matriks, dan meratakan gradien menjadi vektor:

n_params = tf.reduce_prod(layer1.kernel.shape)

g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])

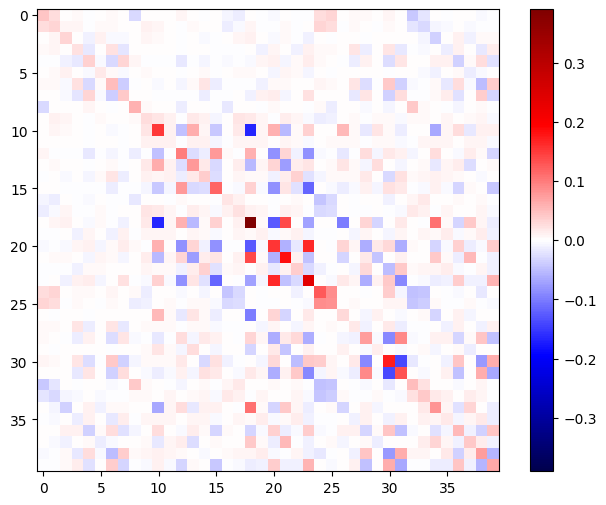
Matriks Hessian harus simetris:

def imshow_zero_center(image, **kwargs):
  lim = tf.reduce_max(abs(image))
  plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
  plt.colorbar()

imshow_zero_center(h_mat)

png

Langkah pembaruan metode Newton ditunjukkan di bawah ini:

eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps

# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)

# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))

Meskipun ini relatif sederhana untuk satu tf.Variable , menerapkan ini pada model non-sepele akan membutuhkan penggabungan dan pemotongan yang cermat untuk menghasilkan Hessian penuh di beberapa variabel.

Batch Jacobian

Dalam beberapa kasus, Anda ingin mengambil Jacobian dari masing-masing tumpukan target sehubungan dengan tumpukan sumber, di mana Jacobian untuk setiap pasangan target-sumber independen.

Misalnya, di sini input x berbentuk (batch, ins) dan output y berbentuk (batch, outs) :

x = tf.random.normal([7, 5])

layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)

with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
  tape.watch(x)
  y = layer1(x)
  y = layer2(y)

y.shape

TensorShape([7, 6])

Jacobian penuh dari y terhadap x memiliki bentuk (batch, ins, batch, outs) , bahkan jika Anda hanya menginginkan (batch, ins, outs) :

j = tape.jacobian(y, x)
j.shape

TensorShape([7, 6, 7, 5])

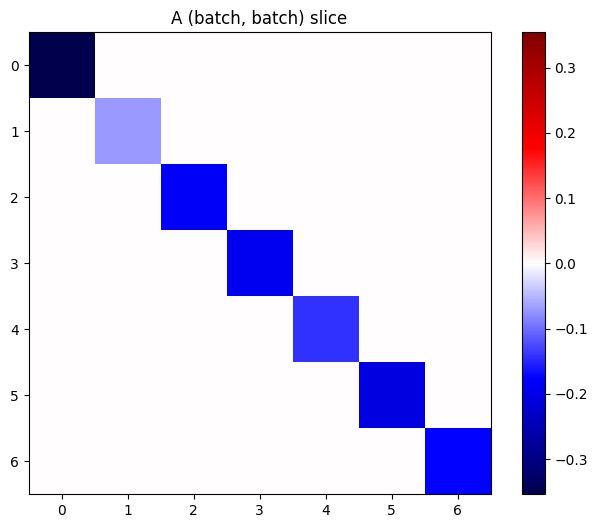
Jika gradien setiap item dalam tumpukan independen, maka setiap irisan (batch, batch) dari tensor ini adalah matriks diagonal:

imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')

png

def plot_as_patches(j):
  # Reorder axes so the diagonals will each form a contiguous patch.
  j = tf.transpose(j, [1, 0, 3, 2])
  # Pad in between each patch.
  lim = tf.reduce_max(abs(j))
  j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
             constant_values=-lim)
  # Reshape to form a single image.
  s = j.shape
  j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
  imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])

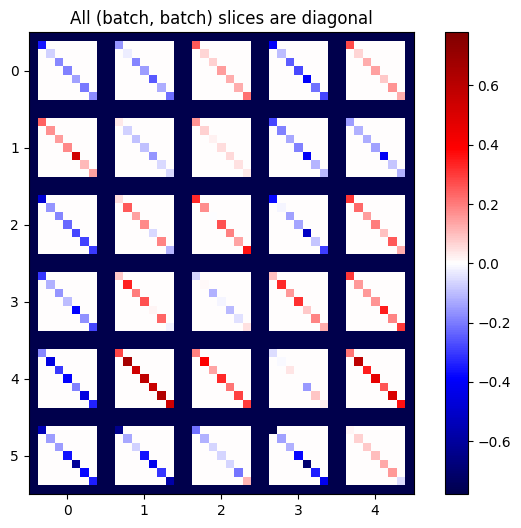
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')

png

Untuk mendapatkan hasil yang diinginkan, Anda dapat menjumlahkan dimensi batch duplikat, atau memilih diagonal menggunakan tf.einsum :

j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)

(7, 6, 5)
(7, 6, 5)

Akan jauh lebih efisien untuk melakukan perhitungan tanpa dimensi tambahan di tempat pertama. Metode tf.GradientTape.batch_jacobian melakukan hal itu:

jb = tape.batch_jacobian(y, x)
jb.shape

WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.
TensorShape([7, 6, 5])

error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())

0.0

x = tf.random.normal([7, 5])

layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)

with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
  tape.watch(x)
  y = layer1(x)
  y = bn(y, training=True)
  y = layer2(y)

j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')

WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.
j.shape: (7, 6, 7, 5)

plot_as_patches(j)

_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")

png

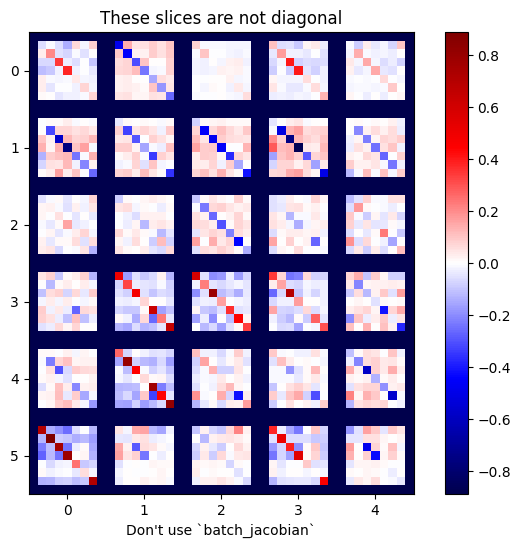
Dalam hal ini, batch_jacobian masih berjalan dan mengembalikan sesuatu dengan bentuk yang diharapkan, tetapi isinya memiliki arti yang tidak jelas:

jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')

jb.shape: (7, 6, 5)