 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar libreta Descargar libreta |
Este tutorial demuestra cómo implementar el método Actor-Critic usando TensorFlow para capacitar a un agente en el entorno Open AI Gym CartPole-V0. Se supone que el lector tiene cierta familiaridad con los métodos de gradiente de políticas de aprendizaje por refuerzo.
Métodos actor-crítico
Los métodos Actor-Crítico son métodos de aprendizaje de diferencia temporal (TD) que representan la función de política independiente de la función de valor.
Una función de política (o política) devuelve una distribución de probabilidad sobre las acciones que el agente puede realizar en función del estado dado. Una función de valor determina el rendimiento esperado para un agente que comienza en un estado dado y actúa de acuerdo con una política particular para siempre.
En el método Actor-Crítico, la política se conoce como el actor que propone un conjunto de posibles acciones dado un estado, y la función de valor estimado se denomina crítica , que evalúa las acciones tomadas por el actor en función de la política dada. .
En este tutorial, tanto el Actor como el Crítico se representarán utilizando una red neuronal con dos salidas.
CartPole-v0
En el entorno CartPole-v0 , se une un poste a un carro que se mueve a lo largo de una pista sin fricción. El poste comienza en posición vertical y el objetivo del agente es evitar que se caiga aplicando una fuerza de -1 o +1 al carro. Se otorga una recompensa de +1 por cada paso de tiempo que el poste permanece en posición vertical. Un episodio termina cuando (1) el poste está a más de 15 grados de la vertical o (2) el carro se mueve a más de 2,4 unidades del centro.
El problema se considera "resuelto" cuando la recompensa total promedio del episodio llega a 195 en 100 intentos consecutivos.
Configuración
Importe los paquetes necesarios y configure los ajustes globales.
pip install gympip install pyglet
# Install additional packages for visualizationsudo apt-get install -y xvfb python-opengl > /dev/null 2>&1pip install pyvirtualdisplay > /dev/null 2>&1pip install git+https://github.com/tensorflow/docs > /dev/null 2>&1
import collections
import gym
import numpy as np
import statistics
import tensorflow as tf
import tqdm
from matplotlib import pyplot as plt
from tensorflow.keras import layers
from typing import Any, List, Sequence, Tuple
# Create the environment
env = gym.make("CartPole-v0")
# Set seed for experiment reproducibility
seed = 42
env.seed(seed)
tf.random.set_seed(seed)
np.random.seed(seed)
# Small epsilon value for stabilizing division operations
eps = np.finfo(np.float32).eps.item()
Modelo
El actor y el crítico se modelarán utilizando una red neuronal que genera las probabilidades de acción y el valor crítico, respectivamente. Este tutorial utiliza subclases de modelos para definir el modelo.
Durante el paso hacia adelante, el modelo tomará el estado como entrada y generará tanto las probabilidades de acción como el valor crítico \(V\), que modela la función de valor dependiente del estado. El objetivo es entrenar un modelo que elija acciones basadas en una política \(\pi\) que maximice el rendimiento esperado.
Para Cartpole-v0, hay cuatro valores que representan el estado: posición del carro, velocidad del carro, ángulo del poste y velocidad del poste, respectivamente. El agente puede realizar dos acciones para empujar el carro hacia la izquierda (0) y hacia la derecha (1) respectivamente.
Consulte la página wiki CartPole-v0 de OpenAI Gym para obtener más información.
class ActorCritic(tf.keras.Model):
"""Combined actor-critic network."""
def __init__(
self,
num_actions: int,
num_hidden_units: int):
"""Initialize."""
super().__init__()
self.common = layers.Dense(num_hidden_units, activation="relu")
self.actor = layers.Dense(num_actions)
self.critic = layers.Dense(1)
def call(self, inputs: tf.Tensor) -> Tuple[tf.Tensor, tf.Tensor]:
x = self.common(inputs)
return self.actor(x), self.critic(x)
num_actions = env.action_space.n # 2
num_hidden_units = 128
model = ActorCritic(num_actions, num_hidden_units)
Capacitación
Para capacitar al agente, deberá seguir estos pasos:
- Ejecute el agente en el entorno para recopilar datos de entrenamiento por episodio.
- Calcule el rendimiento esperado en cada paso de tiempo.
- Calcule la pérdida para el modelo combinado actor-crítico.
- Calcule gradientes y actualice parámetros de red.
- Repita 1-4 hasta alcanzar el criterio de éxito o el número máximo de episodios.
1. Recopilación de datos de entrenamiento
Al igual que en el aprendizaje supervisado, para entrenar el modelo actor-crítico es necesario tener datos de entrenamiento. Sin embargo, para recopilar dichos datos, sería necesario "ejecutar" el modelo en el entorno.
Los datos de entrenamiento se recopilan para cada episodio. Luego, en cada paso de tiempo, el pase hacia adelante del modelo se ejecutará en el estado del entorno para generar probabilidades de acción y el valor crítico basado en la política actual parametrizada por los pesos del modelo.
La siguiente acción se muestreará a partir de las probabilidades de acción generadas por el modelo, que luego se aplicarían al entorno, lo que provocaría la generación del siguiente estado y recompensa.
Este proceso se implementa en la función run_episode , que usa operaciones de TensorFlow para que luego se pueda compilar en un gráfico de TensorFlow para un entrenamiento más rápido. Tenga en cuenta que tf.TensorArray s se usaron para admitir la iteración de Tensor en matrices de longitud variable.
# Wrap OpenAI Gym's `env.step` call as an operation in a TensorFlow function.
# This would allow it to be included in a callable TensorFlow graph.
def env_step(action: np.ndarray) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
"""Returns state, reward and done flag given an action."""
state, reward, done, _ = env.step(action)
return (state.astype(np.float32),
np.array(reward, np.int32),
np.array(done, np.int32))
def tf_env_step(action: tf.Tensor) -> List[tf.Tensor]:
return tf.numpy_function(env_step, [action],
[tf.float32, tf.int32, tf.int32])
def run_episode(
initial_state: tf.Tensor,
model: tf.keras.Model,
max_steps: int) -> Tuple[tf.Tensor, tf.Tensor, tf.Tensor]:
"""Runs a single episode to collect training data."""
action_probs = tf.TensorArray(dtype=tf.float32, size=0, dynamic_size=True)
values = tf.TensorArray(dtype=tf.float32, size=0, dynamic_size=True)
rewards = tf.TensorArray(dtype=tf.int32, size=0, dynamic_size=True)
initial_state_shape = initial_state.shape
state = initial_state
for t in tf.range(max_steps):
# Convert state into a batched tensor (batch size = 1)
state = tf.expand_dims(state, 0)
# Run the model and to get action probabilities and critic value
action_logits_t, value = model(state)
# Sample next action from the action probability distribution
action = tf.random.categorical(action_logits_t, 1)[0, 0]
action_probs_t = tf.nn.softmax(action_logits_t)
# Store critic values
values = values.write(t, tf.squeeze(value))
# Store log probability of the action chosen
action_probs = action_probs.write(t, action_probs_t[0, action])
# Apply action to the environment to get next state and reward
state, reward, done = tf_env_step(action)
state.set_shape(initial_state_shape)
# Store reward
rewards = rewards.write(t, reward)
if tf.cast(done, tf.bool):
break
action_probs = action_probs.stack()
values = values.stack()
rewards = rewards.stack()
return action_probs, values, rewards
2. Cálculo de los rendimientos esperados
La secuencia de recompensas para cada paso de tiempo \(t\), \(\{r_{t}\}^{T}_{t=1}\) recopilada durante un episodio se convierte en una secuencia de rendimientos esperados \(\{G_{t}\}^{T}_{t=1}\) en la que la suma de recompensas se toma del paso de tiempo actual \(t\) a \(T\) y cada la recompensa se multiplica con un factor de descuento exponencialmente decreciente \(\gamma\):
\[G_{t} = \sum^{T}_{t'=t} \gamma^{t'-t}r_{t'}\]
Desde \(\gamma\in(0,1)\), las recompensas más alejadas del paso de tiempo actual tienen menos peso.
Intuitivamente, el rendimiento esperado simplemente implica que las recompensas ahora son mejores que las recompensas posteriores. En un sentido matemático, es para asegurar que la suma de las recompensas converja.
Para estabilizar el entrenamiento, la secuencia resultante de retornos también está estandarizada (es decir, para tener media cero y desviación estándar unitaria).
def get_expected_return(
rewards: tf.Tensor,
gamma: float,
standardize: bool = True) -> tf.Tensor:
"""Compute expected returns per timestep."""
n = tf.shape(rewards)[0]
returns = tf.TensorArray(dtype=tf.float32, size=n)
# Start from the end of `rewards` and accumulate reward sums
# into the `returns` array
rewards = tf.cast(rewards[::-1], dtype=tf.float32)
discounted_sum = tf.constant(0.0)
discounted_sum_shape = discounted_sum.shape
for i in tf.range(n):
reward = rewards[i]
discounted_sum = reward + gamma * discounted_sum
discounted_sum.set_shape(discounted_sum_shape)
returns = returns.write(i, discounted_sum)
returns = returns.stack()[::-1]
if standardize:
returns = ((returns - tf.math.reduce_mean(returns)) /
(tf.math.reduce_std(returns) + eps))
return returns
3. La pérdida actor-crítico
Dado que se utiliza un modelo híbrido actor-crítico, la función de pérdida elegida es una combinación de pérdidas de actor y crítico para el entrenamiento, como se muestra a continuación:
\[L = L_{actor} + L_{critic}\]
Pérdida de actores
La pérdida del actor se basa en gradientes de política con el crítico como una línea de base dependiente del estado y se calcula con estimaciones de muestra única (por episodio).
\[L_{actor} = -\sum^{T}_{t=1} \log\pi_{\theta}(a_{t} | s_{t})[G(s_{t}, a_{t}) - V^{\pi}_{\theta}(s_{t})]\]
donde:
- \(T\): el número de pasos de tiempo por episodio, que puede variar por episodio
- \(s_{t}\): el estado en el paso de tiempo \(t\)
- \(a_{t}\): acción elegida en el paso de tiempo \(t\) dado estado \(s\)
- \(\pi_{\theta}\): es la política (actor) parametrizada por \(\theta\)
- \(V^{\pi}_{\theta}\): es la función de valor (crítica) también parametrizada por \(\theta\)
- \(G = G_{t}\): el rendimiento esperado para un estado dado, par de acciones en el paso de tiempo \(t\)
Se agrega un término negativo a la suma ya que la idea es maximizar las probabilidades de que las acciones produzcan mayores recompensas al minimizar la pérdida combinada.
Ventaja
El término \(G - V\) en nuestra formulación \(L_{actor}\) se llama ventaja , que indica cuánto mejor se le da una acción a un estado particular sobre una acción aleatoria seleccionada de acuerdo con la política \(\pi\) para ese estado.
Si bien es posible excluir una línea base, esto puede resultar en una gran variación durante el entrenamiento. Y lo bueno de elegir el crítico \(V\) como referencia es que entrenó para estar lo más cerca posible de \(G\), lo que lleva a una varianza más baja.
Además, sin la crítica, el algoritmo intentaría aumentar las probabilidades de las acciones realizadas en un estado particular en función del rendimiento esperado, lo que puede no suponer una gran diferencia si las probabilidades relativas entre las acciones siguen siendo las mismas.
Por ejemplo, suponga que dos acciones para un estado dado producirían el mismo rendimiento esperado. Sin la crítica, el algoritmo intentaría aumentar la probabilidad de estas acciones basándose en el \(J\). Con el crítico, puede resultar que no hay ventaja (\(G - V = 0\)) y, por lo tanto, no se obtiene ningún beneficio al aumentar las probabilidades de las acciones y el algoritmo establecería los gradientes en cero.
Pérdida crítica
El entrenamiento \(V\) para que esté lo más cerca posible de \(G\) se puede configurar como un problema de regresión con la siguiente función de pérdida:
\[L_{critic} = L_{\delta}(G, V^{\pi}_{\theta})\]
donde \(L_{\delta}\) es la pérdida de Huber , que es menos sensible a los valores atípicos en los datos que la pérdida por error cuadrático.
huber_loss = tf.keras.losses.Huber(reduction=tf.keras.losses.Reduction.SUM)
def compute_loss(
action_probs: tf.Tensor,
values: tf.Tensor,
returns: tf.Tensor) -> tf.Tensor:
"""Computes the combined actor-critic loss."""
advantage = returns - values
action_log_probs = tf.math.log(action_probs)
actor_loss = -tf.math.reduce_sum(action_log_probs * advantage)
critic_loss = huber_loss(values, returns)
return actor_loss + critic_loss
4. Definición del paso de entrenamiento para actualizar parámetros
Todos los pasos anteriores se combinan en un paso de entrenamiento que se ejecuta en cada episodio. Todos los pasos que conducen a la función de pérdida se ejecutan con el contexto tf.GradientTape para habilitar la diferenciación automática.
Este tutorial utiliza el optimizador de Adam para aplicar los degradados a los parámetros del modelo.
En este paso, también se calcula la suma de las recompensas episode_reward , episodio_recompensa. Este valor se utilizará más adelante para evaluar si se cumple el criterio de éxito.
El contexto tf.function se aplica a la función train_step para que se pueda compilar en un gráfico de TensorFlow invocable, lo que puede generar una aceleración de 10 veces en el entrenamiento.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.01)
@tf.function
def train_step(
initial_state: tf.Tensor,
model: tf.keras.Model,
optimizer: tf.keras.optimizers.Optimizer,
gamma: float,
max_steps_per_episode: int) -> tf.Tensor:
"""Runs a model training step."""
with tf.GradientTape() as tape:
# Run the model for one episode to collect training data
action_probs, values, rewards = run_episode(
initial_state, model, max_steps_per_episode)
# Calculate expected returns
returns = get_expected_return(rewards, gamma)
# Convert training data to appropriate TF tensor shapes
action_probs, values, returns = [
tf.expand_dims(x, 1) for x in [action_probs, values, returns]]
# Calculating loss values to update our network
loss = compute_loss(action_probs, values, returns)
# Compute the gradients from the loss
grads = tape.gradient(loss, model.trainable_variables)
# Apply the gradients to the model's parameters
optimizer.apply_gradients(zip(grads, model.trainable_variables))
episode_reward = tf.math.reduce_sum(rewards)
return episode_reward
5. Ejecute el ciclo de entrenamiento
El entrenamiento se ejecuta ejecutando el paso de entrenamiento hasta que se alcanza el criterio de éxito o el número máximo de episodios.
Se mantiene un registro continuo de las recompensas de los episodios en una cola. Una vez que se alcanzan las 100 pruebas, la recompensa más antigua se elimina en el extremo izquierdo (cola) de la cola y la más nueva se agrega en la cabeza (derecha). También se mantiene una suma acumulada de las recompensas para la eficiencia computacional.
Dependiendo de su tiempo de ejecución, el entrenamiento puede terminar en menos de un minuto.
%%time
min_episodes_criterion = 100
max_episodes = 10000
max_steps_per_episode = 1000
# Cartpole-v0 is considered solved if average reward is >= 195 over 100
# consecutive trials
reward_threshold = 195
running_reward = 0
# Discount factor for future rewards
gamma = 0.99
# Keep last episodes reward
episodes_reward: collections.deque = collections.deque(maxlen=min_episodes_criterion)
with tqdm.trange(max_episodes) as t:
for i in t:
initial_state = tf.constant(env.reset(), dtype=tf.float32)
episode_reward = int(train_step(
initial_state, model, optimizer, gamma, max_steps_per_episode))
episodes_reward.append(episode_reward)
running_reward = statistics.mean(episodes_reward)
t.set_description(f'Episode {i}')
t.set_postfix(
episode_reward=episode_reward, running_reward=running_reward)
# Show average episode reward every 10 episodes
if i % 10 == 0:
pass # print(f'Episode {i}: average reward: {avg_reward}')
if running_reward > reward_threshold and i >= min_episodes_criterion:
break
print(f'\nSolved at episode {i}: average reward: {running_reward:.2f}!')
Episode 361: 4%|▎ | 361/10000 [01:13<32:33, 4.93it/s, episode_reward=182, running_reward=195] Solved at episode 361: average reward: 195.14! CPU times: user 2min 46s, sys: 35.4 s, total: 3min 21s Wall time: 1min 13s
Visualización
Después del entrenamiento, sería bueno visualizar cómo se comporta el modelo en el entorno. Puede ejecutar las celdas a continuación para generar una animación GIF de un episodio del modelo. Tenga en cuenta que es necesario instalar paquetes adicionales para que OpenAI Gym represente correctamente las imágenes del entorno en Colab.
# Render an episode and save as a GIF file
from IPython import display as ipythondisplay
from PIL import Image
from pyvirtualdisplay import Display
display = Display(visible=0, size=(400, 300))
display.start()
def render_episode(env: gym.Env, model: tf.keras.Model, max_steps: int):
screen = env.render(mode='rgb_array')
im = Image.fromarray(screen)
images = [im]
state = tf.constant(env.reset(), dtype=tf.float32)
for i in range(1, max_steps + 1):
state = tf.expand_dims(state, 0)
action_probs, _ = model(state)
action = np.argmax(np.squeeze(action_probs))
state, _, done, _ = env.step(action)
state = tf.constant(state, dtype=tf.float32)
# Render screen every 10 steps
if i % 10 == 0:
screen = env.render(mode='rgb_array')
images.append(Image.fromarray(screen))
if done:
break
return images
# Save GIF image
images = render_episode(env, model, max_steps_per_episode)
image_file = 'cartpole-v0.gif'
# loop=0: loop forever, duration=1: play each frame for 1ms
images[0].save(
image_file, save_all=True, append_images=images[1:], loop=0, duration=1)
import tensorflow_docs.vis.embed as embed
embed.embed_file(image_file)
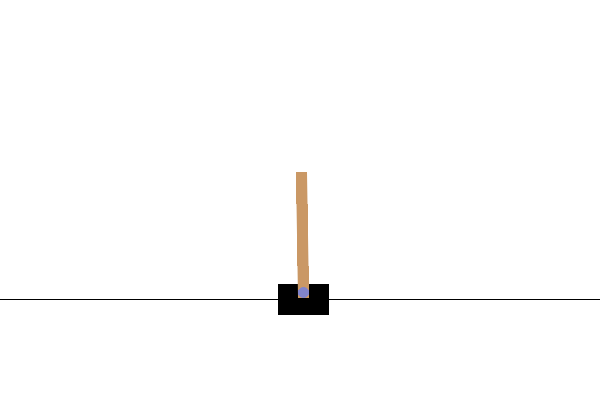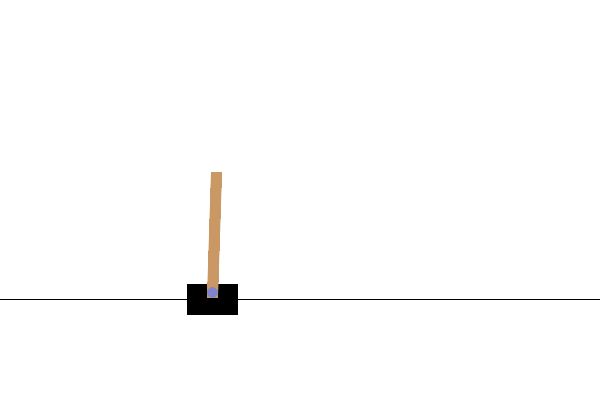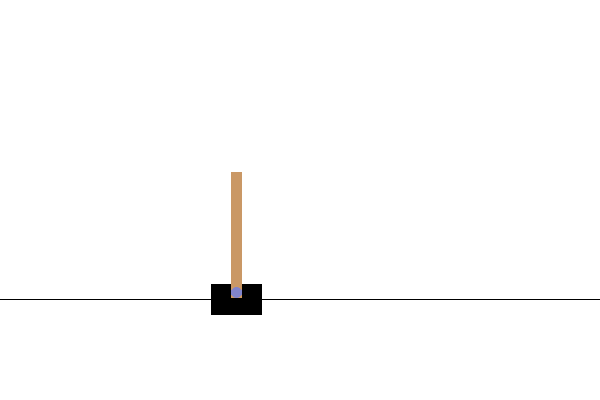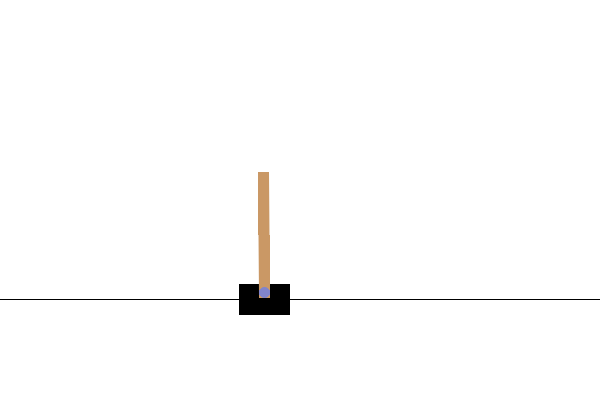
Próximos pasos
Este tutorial demostró cómo implementar el método actor-crítico usando Tensorflow.
Como siguiente paso, podría intentar entrenar a un modelo en un entorno diferente en OpenAI Gym.
Para obtener información adicional sobre los métodos actor-crítico y el problema Cartpole-v0, puede consultar los siguientes recursos:
- Método actor crítico
- Conferencia de crítica de actores (CAL)
- Problema de control de aprendizaje de Cartpole [Barto, et al. 1983]
Para obtener más ejemplos de aprendizaje por refuerzo en TensorFlow, puede consultar los siguientes recursos:
