مدلهای اثرات مختلط خطی

مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

یک مدل اثرات مختلط خطی یک رویکرد ساده برای مدل‌سازی روابط خطی ساخت‌یافته است (Harville، 1997؛ Laird and Ware، 1982). هر نقطه داده متشکل از ورودی هایی با انواع مختلف - دسته بندی شده در گروه ها - و یک خروجی با ارزش واقعی است. مدل اثرات آمیخته خطی مدل سلسله مراتبی است: آن را به اشتراک می گذارد قدرت آماری در سراسر گروه به منظور بهبود استنباط در مورد یکی از نقاط داده است.

در این آموزش، مدل‌های اثرات مختلط خطی را با یک مثال واقعی در TensorFlow Probability نشان می‌دهیم. ما در بر JointDistributionCoroutine و زنجیره مارکوف مونت کارلو (را با استفاده از tfp.mcmc ) ماژول.

وابستگی ها و پیش نیازها

واردات و راه اندازی

import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp

tfd = tfp.distributions
tfb = tfp.bijectors

dtype = tf.float64

%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')

همه چیز را سریع کنید!

قبل از شیرجه رفتن، مطمئن شویم که از یک GPU برای این نسخه نمایشی استفاده می کنیم.

برای انجام این کار، "Runtime" -> "Change runtime type" -> "Hardware accelerator" -> "GPU" را انتخاب کنید.

قطعه زیر تأیید می کند که ما به یک GPU دسترسی داریم.

if tf.test.gpu_device_name() != '/device:GPU:0':
  print('WARNING: GPU device not found.')
else:
  print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))

SUCCESS: Found GPU: /device:GPU:0

داده ها

ما با استفاده از InstEval مجموعه داده از محبوب lme4 بسته در R (بیتس و همکاران، 2015). این مجموعه داده ای از دوره ها و رتبه های ارزیابی آنها است. هر دوره شامل ابرداده مانند students ، instructors ، و departments ، و متغیر پاسخ از علاقه امتیاز ارزیابی است.

def load_insteval():
  """Loads the InstEval data set.

  It contains 73,421 university lecture evaluations by students at ETH
  Zurich with a total of 2,972 students, 2,160 professors and
  lecturers, and several student, lecture, and lecturer attributes.
  Implementation is built from the `observations` Python package.

  Returns:
    Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
    dictionary `metadata` of column headers (feature names).
  """
  url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
         'lme4/InstEval.csv')
  with requests.Session() as s:
    download = s.get(url)
    f = download.content.decode().splitlines()

  iterator = csv.reader(f)
  columns = next(iterator)[1:]
  x_train = np.array([row[1:] for row in iterator], dtype=np.int)
  metadata = {'columns': columns}
  return x_train, metadata

مجموعه داده را بارگیری و پیش پردازش می کنیم. ما 20 درصد از داده ها را نگه می داریم تا بتوانیم مدل برازش شده خود را در نقاط داده نادیده ارزیابی کنیم. در زیر چند ردیف اول را تجسم می کنیم.

data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
                            'd': 'instructors',
                            'dept': 'departments',
                            'y': 'ratings'})
data['students'] -= 1  # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes

train = data.sample(frac=0.8)
test = data.drop(train.index)

train.head()

ما در راه اندازی مجموعه داده ها در شرایط یک features فرهنگ لغت از نهاده ها و labels خروجی مربوط به رتبه بندی. هر ویژگی به عنوان یک عدد صحیح و هر برچسب (رده بندی ارزیابی) به عنوان یک عدد ممیز شناور کدگذاری می شود.

get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
    k: get_value(train, key=k, dtype=np.int32)
    for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)

features_test = {k: get_value(test, key=k, dtype=np.int32)
                 for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)

num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]

print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)

Number of students: 2972
Number of instructors: 1128
Number of departments: 14
Number of observations: 58737

مدل

یک مدل خطی معمولی استقلال را فرض می کند، که در آن هر جفت نقطه داده دارای یک رابطه خطی ثابت است. در InstEval مجموعه داده، مشاهدات در گروه که هر کدام ممکن شیبهای مختلف و ره گیری بوجود می آیند. مدل‌های اثرات مختلط خطی، که به عنوان مدل‌های خطی سلسله مراتبی یا مدل‌های خطی چندسطحی نیز شناخته می‌شوند، این پدیده را به تصویر می‌کشند (گلمن و هیل، 2006).

نمونه هایی از این پدیده عبارتند از:

• دانش آموزان است. مشاهدات یک دانش آموز مستقل نیستند: برخی از دانش آموزان ممکن است به طور سیستماتیک رتبه های سخنرانی پایین (یا بالا) ارائه دهند.
• مربی هستند. مشاهدات یک مربی مستقل نیست: ما انتظار داریم معلمان خوب به طور کلی رتبه های خوب و معلمان بد به طور کلی رتبه بندی بد داشته باشند.
• گروه ها. مشاهدات یک بخش مستقل نیستند: بخش های خاصی ممکن است به طور کلی مواد خشک یا درجه بندی دقیق تری داشته باشند و بنابراین نسبت به سایرین رتبه بندی کمتری دارند.

برای گرفتن این، به یاد بیاورید که برای یک مجموعه داده از \(N\times D\) ویژگی های \(\mathbf{X}\) و \(N\) برچسب \(\mathbf{y}\)، فرض رگرسیون خطی مدل

\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]

است که در آن یک بردار شیب وجود دارد \(\beta\in\mathbb{R}^D\)، رهگیری \(\alpha\in\mathbb{R}\)، و سر و صدا به صورت تصادفی \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). ما می گوییم که \(\beta\) و \(\alpha\) "اثرات ثابت" هستند: آنها اثرات ثابت در سراسر جمعیت از نقاط داده برگزار می شود \((x, y)\). فرمول معادل معادله به عنوان یک احتمال این است \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\). این احتمال است که در طول استنتاج در جهت پیدا کردن برآورد نقطه حداکثر \(\beta\) و \(\alpha\) که در خود جا داده.

یک مدل اثرات مختلط خطی رگرسیون خطی را گسترش می دهد

\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]

که در آن است که هنوز هم یک بردار شیب وجود دارد \(\beta\in\mathbb{R}^P\)، رهگیری \(\alpha\in\mathbb{R}\)، و سر و صدا به صورت تصادفی \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). علاوه بر این، یک اصطلاح وجود دارد \(\mathbf{Z}\eta\)، که در آن \(\mathbf{Z}\) یک ماتریس ویژگی ها و \(\eta\in\mathbb{R}^Q\) یک بردار از دامنه های تصادفی است. \(\eta\) به طور معمول با پارامتر جزء واریانس توزیع \(\sigma^2\). \(\mathbf{Z}\) است با پارتیشن بندی اصلی تشکیل \(N\times D\) ویژگی های ماتریس در نظر جدید \(N\times P\) ماتریس \(\mathbf{X}\) و \(N\times Q\) ماتریس \(\mathbf{Z}\)، که در آن \(P + Q=D\): این پارتیشن به ما امکان میدهد از ویژگی های به طور جداگانه با استفاده از اثرات ثابت \(\beta\) و متغیر پنهان \(\eta\) است.

ما می گوییم متغیرهای نهفته \(\eta\) "اثر تصادفی" هستند: آنها اثرات است که در سراسر جمعیت متفاوت (اگر چه آنها ممکن است ثابت در گروه های جمعیتی) می باشد. به طور خاص، به دلیل اثرات تصادفی \(\eta\) دارند متوسط 0، میانگین برچسب داده ها است که توسط اسیر \(\mathbf{X}\beta + \alpha\). اثرات تصادفی جزء \(\mathbf{Z}\eta\) تغییرات قطاری در داده: "مربی # 54 امتیاز است 1.4 امتیاز بالاتر از میانگین" برای مثال،

در این آموزش، ما افکت های زیر را ارائه می دهیم:

• اثرات ثابت: service . service همبسته باینری مربوط به چه دوره متعلق به بخش اصلی استاد است. مهم نیست که چقدر داده های اضافی جمع آوری می کنیم، تنها می تواند بر ارزش را \(0\) و \(1\).
• اثرات تصادفی: students ، instructors ، و departments . با توجه به مشاهدات بیشتر از جمعیت رتبه‌بندی‌های ارزیابی دوره، ممکن است به دانشجویان، معلمان یا بخش‌های جدید نگاه کنیم.

در نحو بسته lme4 R (بیتس و همکاران، 2015)، مدل را می توان به صورت خلاصه کرد.

ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1

که در آن x نشان دهنده یک اثر ثابت، (1|x) نشان دهنده یک اثر تصادفی برای x و 1 نشان دهنده مدت رهگیری.

ما این مدل را در زیر به صورت JointDistribution پیاده سازی می کنیم. به پشتیبانی بهتر برای ردیابی پارامتر (به عنوان مثال، ما می خواهیم برای پیگیری همه tf.Variable در model.trainable_variables )، ما الگو مدل پیاده سازی tf.Module .

class LinearMixedEffectModel(tf.Module):
  def __init__(self):
    # Set up fixed effects and other parameters.
    # These are free parameters to be optimized in E-steps
    self._intercept = tf.Variable(0., name="intercept")            # alpha in eq
    self._effect_service = tf.Variable(0., name="effect_service")  #  beta in eq
    self._stddev_students = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_students")            # sigma in eq
    self._stddev_instructors = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_instructors")         # sigma in eq
    self._stddev_departments = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_departments")         # sigma in eq

  def __call__(self, features):
    model = tfd.JointDistributionSequential([
      # Set up random effects.
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_students),
          scale_identity_multiplier=self._stddev_students),
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_instructors),
          scale_identity_multiplier=self._stddev_instructors),
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_departments),
          scale_identity_multiplier=self._stddev_departments),
      # This is the likelihood for the observed.
      lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
          tfd.Normal(
              loc=(self._effect_service * features["service"] +
                  tf.gather(effect_students, features["students"], axis=-1) +
                  tf.gather(effect_instructors, features["instructors"], axis=-1) +
                  tf.gather(effect_departments, features["departments"], axis=-1) +
                  self._intercept),
              scale=1.),
              reinterpreted_batch_ndims=1)
    ])

    # To enable tracking of the trainable variables via the created distribution,
    # we attach a reference to `self`. Since all TFP objects sub-class
    # `tf.Module`, this means that the following is possible:
    # LinearMixedEffectModel()(features_train).trainable_variables
    # ==> tuple of all tf.Variables created by LinearMixedEffectModel.
    model._to_track = self
    return model

lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)

lmm_train.trainable_variables

(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)

به عنوان یک برنامه گرافیکی احتمالی، می توانیم ساختار مدل را بر حسب نمودار محاسباتی آن نیز تجسم کنیم. این نمودار جریان داده را در بین متغیرهای تصادفی در برنامه رمزگذاری می کند و روابط آنها را بر اساس یک مدل گرافیکی واضح می کند (جردن، 2003).

به عنوان یک ابزار آماری، ما ممکن است در نمودار در جهت بهتر دید که نگاه کنید، به عنوان مثال، intercept و effect_service مشروط داده وابسته به ratings . اگر برنامه با کلاس‌ها، ارجاعات متقابل در ماژول‌ها و/یا زیر روال‌ها نوشته شده باشد، ممکن است دیدن این از کد منبع سخت‌تر باشد. به عنوان یک ابزار محاسباتی، ما نیز ممکن است متوجه متغیرهای نهفته جریان را به ratings متغیر از طریق tf.gather عملیات. این ممکن است یک گلوگاه در شتاب دهنده های سخت افزاری است اگر نمایه سازی Tensor ها گران است. تجسم نمودار این را به راحتی آشکار می کند.

lmm_train.resolve_graph()

(('effect_students', ()),
 ('effect_instructors', ()),
 ('effect_departments', ()),
 ('x', ('effect_departments', 'effect_instructors', 'effect_students')))

تخمین پارامتر

با توجه به اطلاعات، هدف از استنتاج است به تناسب مدل اثرات ثابت شیب \(\beta\)، رهگیری \(\alpha\)و واریانس پارامتر جزء \(\sigma^2\). اصل حداکثر احتمال این کار را به عنوان رسمیت می بخشد

\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]

در این آموزش، ما از الگوریتم مونت کارلو EM برای به حداکثر رساندن این چگالی حاشیه ای استفاده می کنیم (Dempster et al., 1977; Wei and Tanner, 1990).¹ ما زنجیره مارکوف مونت کارلو را برای محاسبه انتظار احتمال شرطی با توجه به اثرات تصادفی ("E-step")، و ما برای به حداکثر رساندن انتظارات با توجه به پارامترها ("M-step") نزول گرادیان را انجام می دهیم:

• برای مرحله E، همیلتون مونت کارلو (HMC) را راه اندازی کردیم. حالت فعلی را می گیرد - اثرات دانش آموز، مربی و بخش - و حالت جدیدی را برمی گرداند. حالت جدید را به متغیرهای TensorFlow اختصاص می دهیم که نشان دهنده وضعیت زنجیره HMC است.

• برای مرحله M، از نمونه خلفی HMC برای محاسبه یک تخمین بی طرفانه از احتمال نهایی تا یک ثابت استفاده می کنیم. سپس گرادیان آن را با توجه به پارامترهای مورد نظر اعمال می کنیم. این یک گام نزول تصادفی بی‌طرفانه بر روی احتمال حاشیه‌ای ایجاد می‌کند. ما آن را با بهینه ساز Adam TensorFlow پیاده سازی می کنیم و منفی حاشیه را به حداقل می رسانیم.

target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]

# For debugging
target_log_prob_fn(*current_state)

<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>

# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
    target_log_prob_fn=target_log_prob_fn,
    step_size=0.015,
    num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)

@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
  next_state, next_kernel_results = hmc.one_step(
      current_state=current_state,
      previous_kernel_results=kernel_results)
  return next_state, next_kernel_results

optimizer = tf.optimizers.Adam(learning_rate=.01)

# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
  with tf.GradientTape() as tape:
    loss = -target_log_prob_fn(*current_state)
  grads = tape.gradient(loss, trainable_variables)
  optimizer.apply_gradients(zip(grads, trainable_variables))
  return loss

ما یک مرحله گرم کردن را انجام می‌دهیم، که یک زنجیره MCMC را برای تعدادی تکرار اجرا می‌کند، به طوری که آموزش ممکن است در جرم احتمال خلفی مقداردهی اولیه شود. سپس یک حلقه آموزشی اجرا می کنیم. به طور مشترک مراحل E و M را اجرا می کند و مقادیر را در طول تمرین ثبت می کند.

num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])

# Run warm-up stage.
for t in range(num_warmup_iters):
  current_state, kernel_results = one_e_step(current_state, kernel_results)
  num_accepted += kernel_results.is_accepted.numpy()
  if t % 500 == 0 or t == num_warmup_iters - 1:
    print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
        t, num_accepted / (t + 1)))

num_accepted = 0  # reset acceptance rate counter

# Run training.
for t in range(num_iters):
  # run 5 MCMC iterations before every joint EM update
  for _ in range(5):
    current_state, kernel_results = one_e_step(current_state, kernel_results)
  loss = one_m_step(current_state)
  effect_students_samples[t, :] = current_state[0].numpy()
  effect_instructors_samples[t, :] = current_state[1].numpy()
  effect_departments_samples[t, :] = current_state[2].numpy()
  num_accepted += kernel_results.is_accepted.numpy()
  loss_history[t] = loss.numpy()
  if t % 500 == 0 or t == num_iters - 1:
    print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
        t, num_accepted / (t + 1), loss_history[t]))

Warm-Up Iteration:   0 Acceptance Rate: 1.000
Warm-Up Iteration: 500 Acceptance Rate: 0.754
Warm-Up Iteration: 999 Acceptance Rate: 0.707
Iteration:    0 Acceptance Rate: 1.000 Loss: 98220.266
Iteration:  500 Acceptance Rate: 0.703 Loss: 96003.969
Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609
Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891

شما همچنین می توانید گرم کردن حلقه for به یک ارسال tf.while_loop ، و گام آموزش به یک tf.scan یا tf.while_loop حتی سریعتر از استنتاج است. مثلا:

@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
  _, next_state, next_kernel_results = tf.while_loop(
      cond=lambda i, state, pkr: i < k,
      body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
      loop_vars=(tf.constant(0), current_state, kernel_results)
  )
  return next_state, next_kernel_results

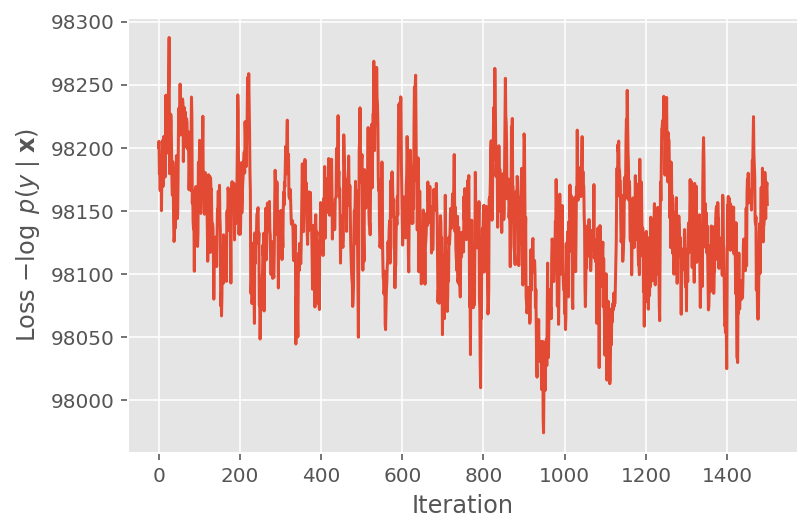
در بالا، ما الگوریتم را تا زمانی که یک آستانه همگرایی شناسایی نشده بود اجرا نکردیم. برای بررسی اینکه آیا آموزش معقول بوده است، تأیید می‌کنیم که تابع ضرر واقعاً تمایل به همگرا شدن با تکرارهای آموزشی دارد.

plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()

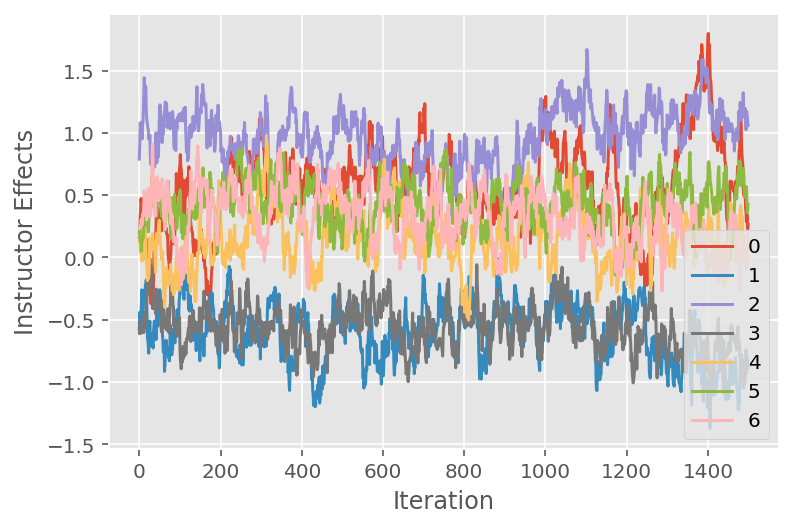
ما همچنین از یک نمودار ردیابی استفاده می کنیم که مسیر الگوریتم مونت کارلو زنجیره مارکوف را در ابعاد پنهان خاص نشان می دهد. در زیر می بینیم که اثرات مربی خاص واقعاً به طور معناداری از حالت اولیه خود دور می شوند و فضای حالت را کشف می کنند. نمودار ردیابی همچنین نشان می دهد که اثرات در بین مربیان متفاوت است اما با رفتار اختلاط مشابه.

for i in range(7):
  plt.plot(effect_instructors_samples[:, i])

plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()

انتقاد

در بالا، ما مدل را نصب کردیم. اکنون به بررسی تناسب آن با استفاده از داده ها می پردازیم، که به ما امکان می دهد مدل را بررسی و بهتر درک کنیم. یکی از این تکنیک‌ها نمودار باقیمانده است که تفاوت بین پیش‌بینی‌های مدل و حقیقت پایه را برای هر نقطه داده ترسیم می‌کند. اگر مدل درست بود، تفاوت آنها باید به طور معمول توزیع استاندارد باشد. هر گونه انحراف از این الگو در نمودار نشان دهنده عدم تناسب مدل است.

ما طرح باقیمانده را با تشکیل توزیع پیش‌بینی پسین بر روی رتبه‌بندی‌ها می‌سازیم، که توزیع قبلی بر روی اثرات تصادفی را با داده‌های آموزشی داده شده پسین آن جایگزین می‌کند. به طور خاص، ما مدل را به جلو اجرا می کنیم و وابستگی آن به اثرات تصادفی قبلی را با میانگین های استنباط شده پسین آنها قطع می کنیم.²

lmm_test = lmm_jointdist(features_test)

[
    effect_students_mean,
    effect_instructors_mean,
    effect_departments_mean,
] = [
     np.mean(x, axis=0).astype(np.float32) for x in [
       effect_students_samples,
       effect_instructors_samples,
       effect_departments_samples
       ]
]

# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
    value=(
        effect_students_mean,
        effect_instructors_mean,
        effect_departments_mean,
))

ratings_prediction = ratings_posterior.mean()

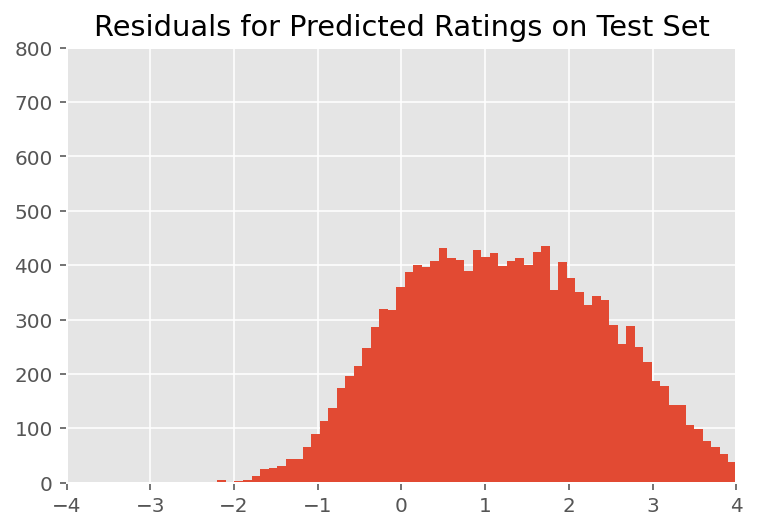
پس از بازرسی بصری، باقیمانده‌ها تا حدودی استاندارد-عادی توزیع شده به نظر می‌رسند. با این حال، تناسب کامل نیست: توده احتمال بیشتری در دم‌ها نسبت به توزیع نرمال وجود دارد، که نشان می‌دهد مدل ممکن است با کاهش مفروضات نرمال بودن، تناسب خود را بهبود بخشد.

به طور خاص، با وجود آن که شایع ترین استفاده از یک توزیع نرمال به رتبه بندی مدل در است InstEval مجموعه داده، نگاهی دقیق تر به این داده ها نشان می دهد که رتبه های ارزیابی دوره در ارزش ترتیبی واقع از 1 تا 5. این نشان می دهد که ما باید با استفاده از یک توزیع ترتیبی، یا حتی اگر داده های کافی برای دور انداختن ترتیب نسبی داشته باشیم، یا حتی دسته بندی. این یک تغییر یک خطی به مدل بالا است. همان کد استنتاج قابل اجرا است.

plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()

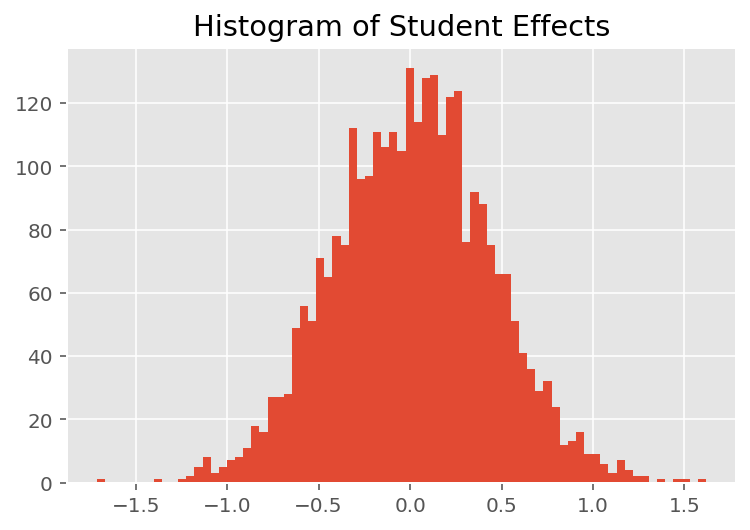
برای کشف اینکه چگونه مدل پیش‌بینی‌های فردی را انجام می‌دهد، به هیستوگرام اثرات برای دانش‌آموزان، مربیان و بخش‌ها نگاه می‌کنیم. این به ما امکان می‌دهد بفهمیم که چگونه عناصر منفرد در بردار ویژگی نقطه داده بر نتیجه تأثیر می‌گذارند.

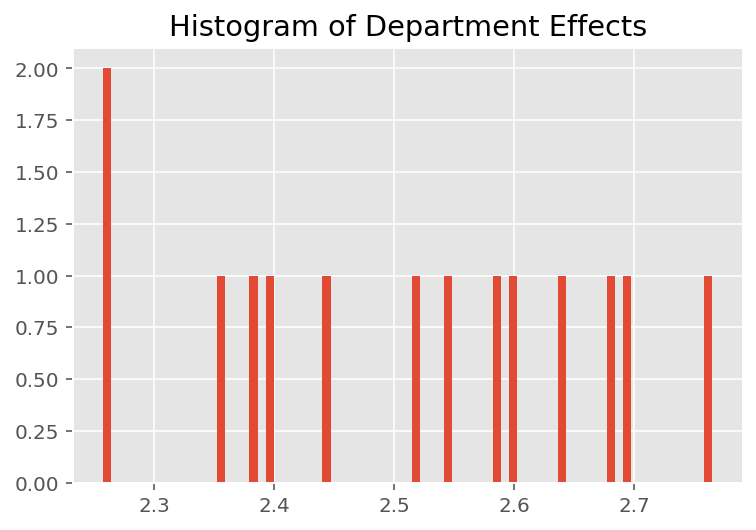
جای تعجب نیست که در زیر می بینیم که هر دانش آموز معمولاً تأثیر کمی بر رتبه ارزشیابی مربی دارد. جالب اینجاست که می بینیم دپارتمانی که یک مربی به آن تعلق دارد تاثیر زیادی دارد.

plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()

plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()

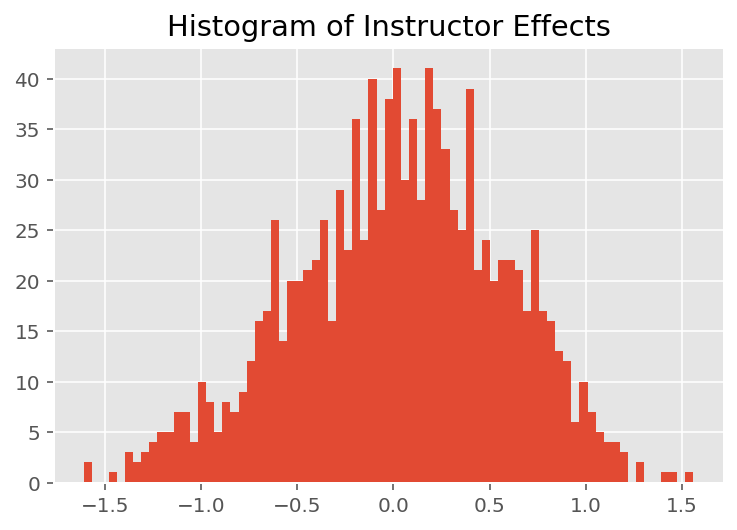
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()

پانویسها و منابع

¹ مدل‌های اثر مختلط خطی مورد خاصی هستند که می‌توانیم چگالی حاشیه‌ای آن را به‌صورت تحلیلی محاسبه کنیم. برای اهداف این آموزش، ما مونت کارلو EM را نشان می‌دهیم، که با سهولت بیشتری برای چگالی‌های حاشیه‌ای غیر تحلیلی اعمال می‌شود، مثلاً اگر احتمال افزایش طبقه‌بندی به جای عادی باشد.

² برای سادگی، میانگین توزیع پیش‌بینی‌کننده را تنها با استفاده از یک پاس رو به جلو از مدل تشکیل می‌دهیم. این با شرطی کردن میانگین خلفی انجام می شود و برای مدل های اثرات مختلط خطی معتبر است. با این حال، این به طور کلی معتبر نیست: میانگین توزیع پیش‌بینی پسین معمولاً غیرقابل حل است و نیاز به گرفتن میانگین تجربی در چندین گذر رو به جلو مدل داده شده در نمونه‌های عقبی دارد.

قدردانی ها

این آموزش در ابتدا در ادوارد 1.0 (نوشته شده بود منبع ). ما از همه مشارکت کنندگان در نوشتن و بازنگری آن نسخه تشکر می کنیم.

منابع

1. داگلاس بیتس و مارتین ماچلر و بن بولکر و استیو واکر. برازش مدل‌های خطی با جلوه‌های ترکیبی با استفاده از lme4. مجله آماری نرم افزار، 67 (1): 1-48، 2015.

2. آرتور پی. دمپستر، نان ام. لیرد و دونالد بی. روبین. حداکثر احتمال داده های ناقص از طریق الگوریتم EM. مجله انجمن سلطنتی آماری، سری B (روش)، 1-38، 1977.

3. اندرو گلمن و جنیفر هیل. تجزیه و تحلیل داده ها با استفاده از رگرسیون و مدل های چندسطحی/سلسله مراتبی. انتشارات دانشگاه کمبریج، 2006.

4. دیوید ای. هارویل. رویکردهای حداکثر احتمال برای برآورد مؤلفه های واریانس و مشکلات مرتبط. مجله انجمن آمار آمریکا، 72 (358): 320-338، 1977.

5. مایکل اول جردن. مقدمه ای بر مدل های گرافیکی گزارش فنی، 2003.

6. نان ام لرد و جیمز ور. مدل‌های اثرات تصادفی برای داده‌های طولی بیومتریک، 963-974، 1982.

7. گرگ وی و مارتین ای تانر. اجرای مونت کارلو از الگوریتم EM و الگوریتم‌های تقویت داده‌های مرد فقیر. مجله انجمن آمار آمریکا، 699-704، 1990.