مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

من این نوت بوک را به عنوان مطالعه موردی برای یادگیری TensorFlow Probability نوشتم. مشکلی که من برای حل آن انتخاب کردم، تخمین یک ماتریس کوواریانس برای نمونه‌های یک متغیر تصادفی گاوسی میانگین 0 دو بعدی است. مشکل چند ویژگی خوب دارد:

• اگر از یک Wishart معکوس قبل برای کوواریانس استفاده کنیم (رویکرد رایج)، مسئله دارای یک راه حل تحلیلی است، بنابراین می توانیم نتایج خود را بررسی کنیم.
• مشکل شامل نمونه برداری از یک پارامتر محدود است که پیچیدگی جالبی را اضافه می کند.
• ساده‌ترین راه‌حل سریع‌ترین راه‌حل نیست، بنابراین باید کارهای بهینه‌سازی انجام داد.

تصمیم گرفتم که تجربیاتم را در ادامه بنویسم. مدتی طول کشید تا سرم را در اطراف نقاط ظریف TFP بپیچم، بنابراین این نوت بوک نسبتاً ساده شروع می شود و سپس به تدریج تا ویژگی های پیچیده تر TFP کار می کند. در طول مسیر به مشکلات زیادی برخورد کردم و سعی کردم هم فرآیندهایی را که به من در شناسایی آنها کمک کردند و هم راه‌حل‌هایی را که در نهایت پیدا کردم، ثبت کنم. من سعی کردم که شامل مقدار زیادی از جزئیات (از جمله تعداد زیادی از آزمایشات مطمئن شوید مراحل فردی درست باشد).

چرا TensorFlow Probability را یاد بگیریم؟

من TensorFlow Probability را برای پروژه خود جذاب دیدم به چند دلیل:

• احتمال TensorFlow به شما امکان می دهد مدل های پیچیده را به صورت تعاملی در یک نوت بوک توسعه دهید. می توانید کد خود را به قطعات کوچک تقسیم کنید که می توانید به صورت تعاملی و با تست های واحد آزمایش کنید.
• هنگامی که آماده افزایش مقیاس شدید، می‌توانید از تمام زیرساخت‌هایی که برای اجرای TensorFlow بر روی چندین پردازنده بهینه‌سازی شده در چندین ماشین در اختیار داریم، استفاده کنید.
• در نهایت، در حالی که من واقعاً استن را دوست دارم، اشکال زدایی برای من بسیار دشوار است. شما باید تمام کدهای مدلسازی خود را به زبانی مستقل بنویسید که ابزارهای کمی دارد که به شما اجازه می دهد کد خود را چک کنید، حالات میانی را بررسی کنید و غیره.

نقطه ضعف این است که TensorFlow Probability بسیار جدیدتر از Stan و PyMC3 است، بنابراین مستندات در حال پیشرفت است و قابلیت‌های زیادی هنوز ساخته نشده است. خوشبختانه، من دریافتم که پایه TFP محکم است، و به روشی مدولار طراحی شده است که به شخص اجازه می دهد تا عملکرد آن را نسبتاً ساده گسترش دهد. در این دفترچه، علاوه بر حل مطالعه موردی، راه هایی را برای گسترش TFP نشان خواهم داد.

این برای کیست

من فرض می کنم که خوانندگان با برخی از پیش نیازهای مهم به سراغ این دفتر می آیند. تو باید:

• اصول استنتاج بیزی را بدانید. (اگر اینکار را نکنید، یک کتاب اول واقعا خوب است آماری بازاندیشی )
• آیا برخی از آشنایی با یک کتابخانه نمونه MCMC، به عنوان مثال استن / PyMC3 / اشکالات
• آیا درک جامد از نامپای (یک معرفی خوب است پایتون برای تجزیه و تحلیل داده )
• حداقل آشنایی عبور با TensorFlow ، اما لزوما تخصص است. ( آموزش TensorFlow خوب است، اما به معنای تکامل سریع TensorFlow است که اکثر آثار تواند یک کمی به تاریخ خواهد شد. استنفورد CS20 البته هم خوب است.)

اولین تلاش

این اولین تلاش من برای حل این مشکل است. اسپویلر: راه حل من کار نمی کند، و چندین تلاش لازم است تا همه چیز درست شود! اگرچه این فرآیند مدتی طول می کشد، اما هر تلاش زیر برای یادگیری بخش جدیدی از TFP مفید بوده است.

یک نکته: TFP در حال حاضر توزیع معکوس Wishart را پیاده سازی نمی کند (ما در پایان خواهیم دید که چگونه Wishart معکوس خودمان را رول کنیم)، بنابراین در عوض من مشکل را به تخمین ماتریس دقیق با استفاده از Wishart قبلی تغییر می دهم.

import collections
import math
import os
import time

import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

مرحله 1: مشاهدات را با هم جمع کنید

داده‌های من در اینجا همگی مصنوعی هستند، بنابراین به نظر می‌رسد این اطلاعات کمی مرتب‌تر از نمونه‌های واقعی به نظر می‌رسد. با این حال، دلیلی وجود ندارد که نتوانید برخی از داده های مصنوعی را خودتان تولید کنید.

نکته: هنگامی که شما در قالب مدل خود را تصمیم گرفته اید، شما می توانید مقادیر پارامتر انتخاب و استفاده از مدل انتخاب شده خود را برای تولید برخی از داده های مصنوعی. به عنوان یک بررسی عقلانی اجرای خود، می توانید تأیید کنید که برآوردهای شما شامل مقادیر واقعی پارامترهایی است که انتخاب کرده اید. برای سریع‌تر کردن چرخه اشکال‌زدایی/تست، می‌توانید یک نسخه ساده‌شده از مدل خود را در نظر بگیرید (مثلاً از ابعاد کمتر یا نمونه‌های کمتر استفاده کنید).

نکته: این ساده ترین راه برای کار را با مشاهدات خود را به عنوان آرایه نامپای. نکته مهمی که باید به آن توجه داشت این است که NumPy به طور پیش فرض از float64 استفاده می کند، در حالی که TensorFlow به طور پیش فرض از float32 استفاده می کند.

به طور کلی، عملیات TensorFlow می‌خواهد همه آرگومان‌ها از یک نوع باشند و برای تغییر نوع باید داده‌های صریح را ارسال کنید. اگر از مشاهدات float64 استفاده می کنید، باید عملیات بازیگری زیادی را اضافه کنید. NumPy، در مقابل، به طور خودکار از ریخته گری مراقبت می کند. از این رو، آن است که بسیار آسان تر برای تبدیل داده های نامپای خود را به float32 از آن است که به زور TensorFlow به استفاده float64.

برخی از مقادیر پارامتر را انتخاب کنید

# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
    np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)

# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))

[[4.  1.8]
 [1.8 1. ]]
eigenvalues:  [4.843075   0.15692513]

برخی مشاهدات مصنوعی ایجاد کنید

توجه داشته باشید که TensorFlow احتمال استفاده از این کنوانسیون که بعد اولیه (بازدید کنندگان) اطلاعات خود را نشان شاخص نمونه، و بعد نهایی (بازدید کنندگان) اطلاعات خود را نشان دهنده ابعاد نمونه خود را.

اینجا ما می خواهیم 100 نمونه، که هر کدام یک بردار به طول است 2. ما یک آرایه تولید my_data با شکل (100، 2). my_data[i, :] است \(i\)هفتم نمونه، و آن را یک بردار به طول 2 است.

(به یاد داشته باشید به my_data از نوع float32!)

# Set the seed so the results are reproducible.
np.random.seed(123)

# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
    mean=true_mean, cov=true_cov, size=100,
    check_valid='ignore').astype(np.float32)

my_data.shape

(100, 2)

سلامتی مشاهدات را بررسی کنید

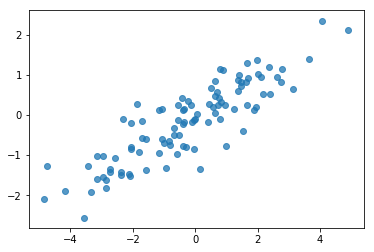
یکی از منابع بالقوه اشکال، به هم ریختن داده های مصنوعی شما است! بیایید چند بررسی ساده انجام دهیم.

# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()

print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)

mean of observations: [-0.24009615 -0.16638893]
true mean: [0. 0.]

print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)

covariance of observations:
 [[3.95307734 1.68718486]
 [1.68718486 0.94910269]]
true covariance:
 [[4.  1.8]
 [1.8 1. ]]

خوب، نمونه های ما معقول به نظر می رسند. گام بعدی.

مرحله 2: تابع احتمال را در NumPy پیاده سازی کنید

اصلی‌ترین چیزی که برای انجام نمونه‌برداری MCMC در TF Probability باید بنویسیم، یک تابع احتمال ورود به سیستم است. به طور کلی نوشتن TF کمی دشوارتر از NumPy است، بنابراین اجرای اولیه در NumPy برای من مفید است. من قصد دارم به تقسیم تابع احتمال به 2 قطعه، یک تابع احتمال داده که مربوط به \(P(data | parameters)\) و یک تابع احتمال قبل که مربوط به \(P(parameters)\).

توجه داشته باشید که این توابع NumPy نیازی به بهینه سازی/بردار شدن فوق العاده ندارند زیرا هدف فقط تولید مقادیری برای آزمایش است. صحت ملاحظات کلیدی است!

ابتدا قطعه احتمال داده ها را پیاده سازی می کنیم. این خیلی ساده است. تنها چیزی که باید به خاطر داشته باشید این است که ما با ماتریس های دقیق کار می کنیم، بنابراین بر این اساس پارامتر بندی می کنیم.

def log_lik_data_numpy(precision, data):
  # np.linalg.inv is a really inefficient way to get the covariance matrix, but
  # remember we don't care about speed here
  cov = np.linalg.inv(precision)
  rv = scipy.stats.multivariate_normal(true_mean, cov)
  return np.sum(rv.logpdf(data))

# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)

-280.81822950593767

ما قصد داریم به استفاده از یک ویشارت قبل برای ماتریس دقت از آنجا که یک راه حل تحلیلی برای خلفی وجود دارد (نگاه کنید به جدول دستی ویکیپدیا مقدم مزدوج ).

توزیع Wishart دارای 2 پارامتر:

• تعداد درجه آزادی (برچسب \(\nu\) در ویکیپدیا)
• یک ماتریس مقیاس (برچسب \(V\) در ویکیپدیا)

میانگین برای یک توزیع Wishart با پارامترهای \(\nu, V\) است \(E[W] = \nu V\)، و واریانس است \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)

برخی شهود مفید: شما می توانید یک نمونه ویشارت با تولید تولید \(\nu\) مستقل تساوی \(x_1 \ldots x_{\nu}\) از یک متغیر تصادفی نرمال چند متغیره با میانگین 0 و کوواریانس \(V\) و سپس تشکیل مجموع \(W = \sum_{i=1}^{\nu} x_i x_i^T\).

اگر شما تغییر اندازه ی نمونه ویشارت با تقسیم آنها را با \(\nu\)، شما می ماتریس کواریانس نمونه از گرفتن \(x_i\). این ماتریس کوواریانس نمونه باید به سمت تمایل \(V\) عنوان \(\nu\) افزایش می یابد. هنگامی که \(\nu\) کوچک است، تعداد زیادی از تغییر در ماتریس کوواریانس نمونه، ارزش آنقدر کوچک وجود دارد \(\nu\) مربوط به priors ضعیف تر و مقادیر بزرگ \(\nu\) مربوط به priors قوی تر. توجه داشته باشید که \(\nu\) باید حداقل به عنوان بزرگ به عنوان بعد از فضای شما نمونه هستید و یا شما ماتریس منحصر به فرد تولید می شود.

ما استفاده از \(\nu = 3\) بنابراین ما باید ضعیف قبل، و ما را \(V = \frac{1}{\nu} I\) که برآورد کوواریانس ما نسبت به هویت جلو (به یاد بیاورید که میانگین است \(\nu V\)).

PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF

def log_lik_prior_numpy(precision):
  rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
  return rv.logpdf(precision)

# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)

-9.103606346649766

توزیع Wishart مزدوج قبل برای تخمین ماتریس دقت یک نرمال چند متغیره با شناخته شده است متوسط \(\mu\).

فرض پارامترهای ویشارت قبل هستند \(\nu, V\) و این که ما \(n\) مشاهدات ما چند متغیره نرمال، \(x_1, \ldots, x_n\). پارامترهای خلفی هستند \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).

n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
                       (v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))

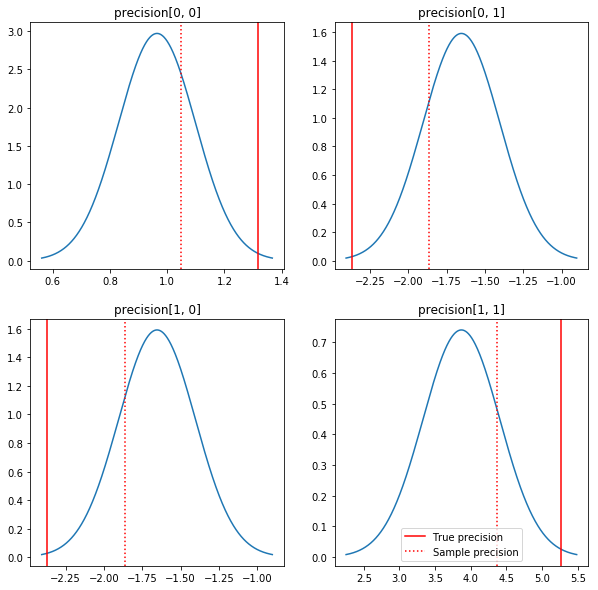
طرحی سریع از پسین ها و ارزش های واقعی. توجه داشته باشید که پسین ها نزدیک به نمونه های خلفی هستند اما کمی به سمت هویت کوچک شده اند. همچنین توجه داشته باشید که مقادیر واقعی بسیار دور از حالت پسین هستند - احتمالاً این به این دلیل است که prior تطابق چندانی با داده‌های ما ندارد. در یک مشکل واقعی ما به احتمال زیاد می خواهم انجام بهتر با چیزی شبیه به یک مقیاس معکوس ویشارت قبل برای کوواریانس (نگاه کنید به، برای مثال، اندرو Gelman را تفسیر در مورد این موضوع)، اما آن گاه خلفی تحلیلی خوب ندارد.

sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    loc = posterior_mean[i, j]
    scale = posterior_sd[i, j]
    xmin = loc - 3.0 * scale
    xmax = loc + 3.0 * scale
    x = np.linspace(xmin, xmax, 1000)
    y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
    ax.plot(x, y)
    ax.axvline(true_precision[i, j], color='red', label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()

مرحله 3: تابع احتمال را در TensorFlow پیاده سازی کنید

اسپویلر: اولین تلاش ما کارساز نیست. در زیر در مورد چرایی صحبت خواهیم کرد.

نکته: استفاده از حالت TensorFlow مشتاق که در حال توسعه توابع احتمال خود را. حالت مشتاق می سازد رفتار TF بیشتر شبیه نامپای - اجرا همه چیز را بلافاصله، بنابراین شما می توانید تعاملی به جای نیاز به استفاده از اشکال زدایی Session.run() . یادداشت را ببینید در اینجا .

مقدماتی: کلاس های توزیع

TFP مجموعه ای از کلاس های توزیع دارد که ما از آنها برای تولید احتمالات لاگ خود استفاده خواهیم کرد. نکته‌ای که باید به آن توجه داشت این است که این کلاس‌ها با تانسور نمونه‌ها کار می‌کنند نه فقط نمونه‌های منفرد - این امکان بردارسازی و سرعت‌های مرتبط را فراهم می‌کند.

یک توزیع می تواند با تانسور نمونه ها به 2 روش مختلف کار کند. ساده‌ترین راه برای نشان دادن این دو روش با یک مثال عینی که شامل توزیع با یک پارامتر اسکالر است. من از آن استفاده پواسون توزیع، که دارای یک rate پارامتر.

• اگر ما یک پواسون ایجاد با یک ارزش واحد برای rate پارامتر، یک تماس به آن sample() روش بازگشت به یک مقدار واحد است. این مقدار به نام event ، و در این مورد از حوادث تمام بندی هستند.
• اگر ما یک پواسون ایجاد با یک تانسور از ارزش ها برای rate پارامتر، یک تماس به آن sample() روش در حال حاضر چندین مقدار را برمی گرداند، یکی برای هر ارزش در تانسور نرخ است. شی به عنوان یک مجموعه ای از Poissons مستقل، هر کدام با نرخ خود عمل می کند، و هر یک از مقادیر توسط یک تماس بازگشت به sample() مربوط به یکی از این Poissons. این مجموعه ای از رویداد مستقل اما نه یکسان توزیع شده است که به نام batch .
• sample() روش طول می کشد یک sample_shape پارامتر را که به صورت پیش فرض به تاپل خالی است. عبور از یک مقدار خالی برای sample_shape نتایج در نمونه بازگشت دسته های متعدد. این مجموعه که از دسته های است که به نام sample .

یک توزیع را log_prob() روش مصرف داده در شیوه ای که تشابه چگونه sample() آن را تولید. log_prob() احتمال برای نمونه، به عنوان مثال برای متعدد، دسته مستقل از حوادث می گرداند.

• اگر ما جسم پواسون ما که با یک اسکالر ایجاد شد rate ، هر دسته یک اسکالر است، و اگر ما در یک تانسور از نمونه عبور می کند، ما را از دریافت یک تانسور از همان اندازه احتمال ورود به سیستم.
• اگر ما جسم پواسون ما که با یک تانسور از شکل ایجاد شد T از rate ارزش ها، هر دسته یک تانسور شکل است T . اگر تانسوری از نمونه‌های شکل D، T را وارد کنیم، تانسور احتمالات لاگ شکل D، T را بیرون می‌آوریم.

در زیر چند نمونه آورده شده است که این موارد را نشان می دهد. مشاهده این نوت بوک برای آموزش بیشتر در حوادث، دسته، و اشکال.

# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))

# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters.  Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))

print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())

iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385]
draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]

احتمال ثبت داده ها

ابتدا تابع احتمال ثبت داده ها را پیاده سازی می کنیم.

VALIDATE_ARGS = True
ALLOW_NAN_STATS = False

یک تفاوت کلیدی با مورد NumPy این است که تابع درستنمایی TensorFlow ما باید به جای ماتریس های منفرد، بردارهای ماتریس های دقیق را مدیریت کند. هنگامی که از چندین زنجیره نمونه برداری می کنیم، بردار پارامترها استفاده می شود.

ما یک شی توزیع ایجاد می کنیم که با دسته ای از ماتریس های دقیق کار می کند (یعنی یک ماتریس در هر زنجیره).

هنگام محاسبه احتمالات گزارش داده‌هایمان، باید داده‌هایمان همانند پارامترهایمان تکرار شوند تا یک کپی در هر متغیر دسته‌ای وجود داشته باشد. شکل داده های تکراری ما باید به صورت زیر باشد:

[sample shape, batch shape, event shape]

در مورد ما، شکل رویداد 2 است (از آنجایی که ما با گاوسیان دو بعدی کار می کنیم). شکل نمونه 100 است، زیرا ما 100 نمونه داریم. شکل دسته ای فقط تعداد ماتریس های دقیقی است که با آنها کار می کنیم. هر بار که تابع درستنمایی را فراخوانی می‌کنیم، تکرار داده‌ها بیهوده است، بنابراین داده‌ها را از قبل تکرار می‌کنیم و در نسخه تکراری ارسال می‌کنیم.

توجه داشته باشید که این یک پیاده سازی ناکارآمد است: MultivariateNormalFullCovariance نسبی گران به برخی از گزینه های که ما در مورد در بخش بهینه سازی در پایان صحبت است.

def log_lik_data(precisions, replicated_data):
  n = tf.shape(precisions)[0]  # number of precision matrices
  # We're estimating a precision matrix; we have to invert to get log
  # probabilities.  Cholesky inversion should be relatively efficient,
  # but as we'll see later, it's even better if we can avoid doing the Cholesky
  # decomposition altogether.
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data).  We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)

(100, 2, 2)

نکته: یک چیزی که من پیدا کرده ام می شود بسیار مفید است نوشتن چک سلامت عقل کمی از توابع TensorFlow من. به هم ریختن وکتورسازی در TF بسیار آسان است، بنابراین داشتن توابع ساده‌تر NumPy راهی عالی برای تأیید خروجی TF است. اینها را به عنوان آزمون های واحد کوچک در نظر بگیرید.

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

احتمال ورود به سیستم قبلی

قبل آسان تر است زیرا ما نیازی به نگرانی در مورد تکرار داده نداریم.

@tf.function(autograph=False)
def log_lik_prior(precisions):
  rv_precision = tfd.WishartTriL(
      df=PRIOR_DF,
      scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions)

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]))
  print('tensorflow:', lik_tf[i])

0
numpy: -2.2351873809649625
tensorflow: -2.2351875
1
numpy: -9.103606346649766
tensorflow: -9.103608

تابع درستنمایی گزارش مشترک را بسازید

تابع احتمال ثبت داده در بالا به مشاهدات ما بستگی دارد، اما نمونه‌بردار آن‌ها را نخواهد داشت. ما می‌توانیم با استفاده از [closure] (https://en.wikipedia.org/wiki/Closure_(computer_programming) بدون استفاده از یک متغیر سراسری از شر وابستگی خلاص شویم. بسته‌ها شامل یک تابع بیرونی است که محیطی حاوی متغیرهای مورد نیاز یک عملکرد درونی

def get_log_lik(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik(precision):
    return log_lik_data(precision, replicated_data) + log_lik_prior(precision)

  return _log_lik

مرحله 4: نمونه

خوب، وقت نمونه گیری است! برای ساده نگه داشتن چیزها، ما فقط از 1 زنجیره استفاده می کنیم و از ماتریس هویت به عنوان نقطه شروع استفاده می کنیم. بعداً کارها را با دقت بیشتری انجام خواهیم داد.

باز هم، این کار نمی کند - ما یک استثنا خواهیم داشت.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.expand_dims(tf.eye(2), axis=0)

  # Use expand_dims because we want to pass in a tensor of starting values
  log_lik_fn = get_log_lik(my_data, n_chains=1)

  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
     num_results=num_results,
     num_burnin_steps=num_burnin_steps,
     current_state=[
         init_precision,
     ],
     kernel=tfp.mcmc.HamiltonianMonteCarlo(
         target_log_prob_fn=log_lik_fn,
         step_size=0.1,
         num_leapfrog_steps=3),
     trace_fn=None,
     seed=123)
  return states

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

Cholesky decomposition was not successful. The input might not be valid.
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]

Function call stack:
sample
...
Function call stack:
sample

شناسایی مشکل

InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. این فوق العاده مفید نیست. بیایید ببینیم که آیا می توانیم بیشتر در مورد آنچه اتفاق افتاده است بدانیم.

• ما پارامترهای هر مرحله را چاپ می کنیم تا بتوانیم مقداری را که برای آن چیزها خراب می شوند، ببینیم
• برای محافظت در برابر مشکلات خاص، برخی ادعاها را اضافه خواهیم کرد.

ادعاها مشکل هستند زیرا عملیات TensorFlow هستند و ما باید مراقب باشیم که اجرا شوند و از نمودار بهینه نشوند. ارزش آن را خواندن این بررسی اجمالی از اشکال زدایی TensorFlow اگر شما با استفاده از اظهارات TF آشنا نیست. شما می توانید به صراحت اظهارات را مجبور به اجرا با استفاده از tf.control_dependencies (نگاه کنید به نظر در کد زیر).

مادری TensorFlow را Print تابع همان رفتار به عنوان اظهارات - آن یک عملیات است، و شما نیاز به برخی از مراقبت به اطمینان حاصل شود که آن را اجرا می کند. Print باعث سردرد های اضافی هنگامی که ما در حال کار در یک نوت بوک: خروجی مورد نظر برای ارسال stderr ، و stderr در سلول نمایش داده نمی شود. ما یک ترفند در اینجا استفاده کنید: به جای استفاده از tf.Print ، ما خود عمل TensorFlow چاپ ما از طریق ایجاد tf.pyfunc . همانطور که در مورد ادعاها، ما باید مطمئن شویم که روش ما اجرا می شود.

def get_log_lik_verbose(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  def _log_lik(precisions):
    # An internal method we'll make into a TensorFlow operation via tf.py_func
    def _print_precisions(precisions):
      print('precisions:\n', precisions)
      return False  # operations must return something!
    # Turn our method into a TensorFlow operation
    print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)

    # Assertions are also operations, and some care needs to be taken to ensure
    # that they're executed
    assert_op = tf.assert_equal(
        precisions, tf.linalg.matrix_transpose(precisions),
        message='not symmetrical', summarize=4, name='symmetry_check')

    # The control_dependencies statement forces its arguments to be executed
    # before subsequent operations
    with tf.control_dependencies([print_op, assert_op]):
      return (log_lik_data(precisions, replicated_data) +
              log_lik_prior(precisions))

  return _log_lik

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.eye(2)[tf.newaxis, ...]
  log_lik_fn = get_log_lik_verbose(my_data)
  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          init_precision,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=None,
      seed=123)

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[ 0.24315196 -0.2761638 ]
  [-0.33882257  0.8622    ]]]
 assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]

Function call stack:
sample
...
Function call stack:
sample

چرا این شکست می خورد

اولین مقدار پارامتر جدیدی که نمونه‌گر امتحان می‌کند، یک ماتریس نامتقارن است. این باعث می شود که تجزیه Cholesky شکست بخورد، زیرا فقط برای ماتریس های متقارن (و قطعی مثبت) تعریف شده است.

مشکل اینجاست که پارامتر مورد نظر ما یک ماتریس دقیق است و ماتریس های دقیق باید واقعی، متقارن و قطعی مثبت باشند. نمونه‌گر چیزی در مورد این محدودیت نمی‌داند (به جز احتمالاً از طریق گرادیان)، بنابراین کاملاً ممکن است که نمونه‌گر مقدار نامعتبری را پیشنهاد کند، به‌ویژه اگر اندازه مرحله بزرگ باشد.

با نمونه‌بردار همیلتونی مونت کارلو، ممکن است بتوانیم با استفاده از اندازه گام بسیار کوچک، مشکل را حل کنیم، زیرا گرادیان باید پارامترها را از مناطق نامعتبر دور نگه دارد، اما اندازه‌های گام کوچک به معنای همگرایی آهسته است. با یک نمونه‌بردار Metropolis-Hastings، که چیزی در مورد گرادیان نمی‌داند، محکوم به فنا هستیم.

نسخه 2: reparametrizing به پارامترهای بدون محدودیت

یک راه حل ساده برای مشکل بالا وجود دارد: ما می توانیم مدل خود را مجدداً پارامتر کنیم به طوری که پارامترهای جدید دیگر این محدودیت ها را نداشته باشند. TFP مجموعه ای مفید از ابزارها - بیجکتورها - را برای انجام این کار فراهم می کند.

پارامترسازی مجدد با بیژکتور

ماتریس دقیق ما باید واقعی و متقارن باشد. ما یک پارامتر جایگزینی می خواهیم که این محدودیت ها را نداشته باشد. یک نقطه شروع، فاکتورسازی Cholesky از ماتریس دقیق است. عوامل Cholesky هنوز محدود هستند - آنها مثلثی پایین تر هستند و عناصر مورب آنها باید مثبت باشند. با این حال، اگر لاگ قطرهای ضریب Cholesky را در نظر بگیریم، لاگ ها دیگر محدود به مثبت بودن نیستند، و سپس اگر قسمت مثلث پایینی را به یک بردار 1 بعدی صاف کنیم، دیگر محدودیت مثلثی پایینی نداریم. . نتیجه در مورد ما یک بردار طول 3 بدون محدودیت خواهد بود.

(این کتابچه راهنمای کاربر استن یک فصل بزرگ در استفاده از تبدیلات به حذف انواع مختلفی از محدودیت بر پارامترهای.)

این پارامترسازی مجدد تأثیر کمی بر تابع احتمال گزارش داده ما دارد - ما فقط باید تبدیل خود را معکوس کنیم تا ماتریس دقیق را برگردانیم - اما تأثیر روی قبلی پیچیده تر است. ما مشخص کرده‌ایم که احتمال یک ماتریس دقیق با توزیع Wishart داده می‌شود. احتمال ماتریس تبدیل شده ما چقدر است؟

به یاد بیاورید که اگر ما یک تابع یکنواخت \(g\) به 1-D متغیر تصادفی \(X\)، \(Y = g(X)\)، چگالی برای \(Y\) داده شده است

\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]

مشتق \(g^{-1}\) مدت حساب برای راه که \(g\) تغییر حجم محلی است. برای متغیرهای تصادفی بالاتر بعدی، عامل اصلاحی ارزش مطلق تعیین کننده در ژاکوبین است \(g^{-1}\) (نگاه کنید به اینجا ).

ما باید یک ژاکوبین از تبدیل معکوس را به تابع درستنمایی قبل از ثبت خود اضافه کنیم. خوشبختانه، بهره وری کل عوامل را Bijector کلاس می تواند مراقبت از این برای ما را.

Bijector کلاس استفاده می شود برای نشان معکوس، توابع هموار استفاده برای تغییر متغیر در تابع چگالی احتمال. Bijectors همه دارند forward() روش است که انجام یک تبدیل، یک inverse() روش که معکوس آن، و forward_log_det_jacobian() و inverse_log_det_jacobian() روش هایی که ارائه اصلاحات ژاکوبین ما باید زمانی که ما reparaterize پی دی اف.

بهره وری کل عوامل مجموعه ای از bijectors مفید است که ما می توانید از طریق ترکیب از طریق ترکیب فراهم می کند Chain اپراتور به شکل تبدیل کاملا پیچیده است. در مورد ما، ما 3 بیژکتور زیر را می سازیم (عملیات زنجیره از راست به چپ انجام می شود):

1. اولین مرحله تبدیل ما انجام فاکتورسازی Cholesky بر روی ماتریس دقیق است. کلاس Bijector برای آن وجود ندارد. با این حال، CholeskyOuterProduct bijector طول می کشد کالا از 2 عوامل Cholesky. ما می توانیم معکوس که عملیات با استفاده از استفاده Invert اپراتور.
2. گام بعدی گرفتن لاگ عناصر مورب عامل Cholesky است. ما این کار را از طریق TransformDiagonal bijector و معکوس از Exp bijector.
3. در نهایت ما بخش مثلثی پایین تر از ماتریس پهن به یک بردار با استفاده از معکوس از FillTriangular bijector.

# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
    # step 3: flatten the lower triangular portion of the matrix
    tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
    # step 2: take the log of the diagonals    
    tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
    # step 1: decompose the precision matrix into its Cholesky factors
    tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])

# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)

# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)

print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()

print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())

single input:
m:
 [[1. 2.]
 [2. 8.]]
precision_to_unconstrained(m):
 [0.6931472 2.        0.       ]
inverse(precision_to_unconstrained(m)):
 [[1. 2.]
 [2. 8.]]

tensor of inputs:
m2:
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]
precision_to_unconstrained(m2):
 [[0.6931472 2.        0.       ]
 [0.        0.        0.       ]]
inverse(precision_to_unconstrained(m2)):
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]

TransformedDistribution کلاس خودکار فرآیند استفاده از یک bijector به یک توزیع و اصلاح ژاکوبین لازم برای log_prob() . پیشین جدید ما می شود:

def log_lik_prior_transformed(transformed_precisions):
  rv_precision = tfd.TransformedDistribution(
      tfd.WishartTriL(
          df=PRIOR_DF,
          scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
          validate_args=VALIDATE_ARGS,
          allow_nan_stats=ALLOW_NAN_STATS),
      bijector=precision_to_unconstrained,
      validate_args=VALIDATE_ARGS)
  return rv_precision.log_prob(transformed_precisions)

# Check against the numpy implementation.  Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
    transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow: -0.84889317
1
numpy: -7.305657151741624
tensorflow: -7.305659

ما فقط باید تبدیل را برای احتمال گزارش داده خود معکوس کنیم:

precision = precision_to_unconstrained.inverse(transformed_precision)

از آنجایی که ما واقعاً فاکتورسازی Cholesky ماتریس دقیق را می‌خواهیم، ​​انجام یک معکوس جزئی در اینجا کارآمدتر خواهد بود. با این حال، ما بهینه سازی را برای بعد می گذاریم و معکوس جزئی را به عنوان تمرینی برای خواننده باقی می گذاریم.

def log_lik_data_transformed(transformed_precisions, replicated_data):
  # We recover the precision matrix by inverting our bijector.  This is
  # inefficient since we really want the Cholesky decomposition of the
  # precision matrix, and the bijector has that in hand during the inversion,
  # but we'll worry about efficiency later.
  n = tf.shape(transformed_precisions)[0]
  precisions = precision_to_unconstrained.inverse(transformed_precisions)
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
    transformed_precisions, replicated_data).numpy()

for i in range(precisions.shape[0]):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

دوباره توابع جدید خود را در یک بسته می بندیم.

def get_log_lik_transformed(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_transformed(transformed_precisions):
    return (log_lik_data_transformed(transformed_precisions, replicated_data) +
            log_lik_prior_transformed(transformed_precisions))

  return _log_lik_transformed

# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)

[-431.5611]

نمونه برداری

اکنون که لازم نیست نگران انفجار نمونه‌گر خود به دلیل مقادیر نامعتبر پارامتر باشیم، بیایید چند نمونه واقعی تولید کنیم.

نمونه‌گر با نسخه بدون محدودیت پارامترهای ما کار می‌کند، بنابراین باید مقدار اولیه خود را به نسخه بدون محدودیت آن تبدیل کنیم. نمونه‌هایی که تولید می‌کنیم همگی به شکل نامحدود خود خواهند بود، بنابراین باید آن‌ها را برگردانیم. بیژکتورها بردار هستند، بنابراین انجام این کار آسان است.

# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
    [[0.5 + np.random.uniform(), 0.0],
     [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
    dtype=np.float32)
initial_value =  initial_value_cholesky.dot(
  initial_value_cholesky.T)[np.newaxis, ...]

# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
  initial_value).numpy()

# Sample!
@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)

  num_results = 1000
  num_burnin_steps = 1000

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          initial_value_transformed,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=lambda _, pkr: pkr.is_accepted,
      seed=123)
  # transform samples back to their constrained form
  precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

بیایید میانگین خروجی نمونه‌گر خود را با میانگین تحلیلی پسین مقایسه کنیم!

print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Sample mean:
 [[ 1.4315274  -0.25587553]
 [-0.25587553  0.5740424 ]]

ما خیلی دوریم! بیایید بفهمیم چرا ابتدا به نمونه های خود نگاه می کنیم.

np.reshape(precision_samples, [-1, 2, 2])

array([[[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       ...,

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]]], dtype=float32)

اوه اوه - به نظر می رسد همه آنها ارزش یکسانی دارند. بیایید بفهمیم چرا

kernel_results_ متغیر یک تاپل نام برد که اطلاعات در مورد نمونه در هر ایالت می دهد است. is_accepted زمینه کلیدی در اینجا است.

# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))

[False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False]
Fraction of samples accepted: 0.0

همه نمونه های ما رد شد! احتمالاً اندازه گام ما خیلی بزرگ بود. من انتخاب stepsize=0.1 کاملا خودسرانه.

نسخه 3: نمونه برداری با اندازه گام تطبیقی

از آنجایی که نمونه برداری با انتخاب دلخواه من برای اندازه مرحله ناموفق بود، چند مورد دستور کار داریم:

1. پیاده سازی اندازه گام تطبیقی، و
2. انجام برخی بررسی های همگرایی

است برخی از نمونه کد خوبی در آن وجود tensorflow_probability/python/mcmc/hmc.py برای اجرای اندازه گام تطبیقی. من آن را در زیر اقتباس کرده ام.

توجه داشته باشید که یک جداگانه وجود دارد sess.run() بیانیه برای هر مرحله. این واقعاً برای اشکال‌زدایی مفید است، زیرا به ما امکان می‌دهد در صورت نیاز به راحتی برخی از تشخیص‌های هر مرحله را اضافه کنیم. به عنوان مثال، می توانیم پیشرفت تدریجی، زمان هر مرحله و غیره را نشان دهیم.

نکته: یکی از راه های به ظاهر متعارف به یک ظرف غذا تا نمونه شما این است که رشد نمودار خود را در حلقه. (دلیل نهایی کردن نمودار قبل از اجرای جلسه، جلوگیری از چنین مشکلاتی است.) اگر از finalize() استفاده نکرده اید، یک بررسی مفید اشکال زدایی اگر کد شما به سمت خزیدن کند می شود، چاپ کردن نمودار است. اندازه در هر مرحله از طریق len(mygraph.get_operations()) - اگر افزایش طول، شما احتمالا انجام کاری بد است.

ما می خواهیم 3 زنجیره مستقل را در اینجا راه اندازی کنیم. انجام برخی مقایسه ها بین زنجیره ها به ما کمک می کند تا همگرایی را بررسی کنیم.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values = []
for i in range(N_CHAINS):
  initial_value_cholesky = np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32)
  initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)

initial_values_transformed = precision_to_unconstrained.forward(
  initial_values).numpy()

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=hmc,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values_transformed,
      kernel=adapted_kernel,
      trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
      parallel_iterations=1)
  # transform samples back to their constrained form
  precision_samples = precision_to_unconstrained.inverse(states)
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

یک بررسی سریع: نرخ پذیرش ما در طول نمونه‌برداری نزدیک به هدف ما 0.651 است.

print(np.mean(is_accepted))

0.6190666666666667

حتی بهتر از آن، میانگین نمونه و انحراف معیار ما به آنچه از راه حل تحلیلی انتظار داریم نزدیک است.

precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96426415 -1.6519215 ]
 [-1.6519215   3.8614824 ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13622096 0.25235635]
 [0.25235635 0.5394968 ]]

بررسی همگرایی

به طور کلی، ما یک راه حل تحلیلی برای بررسی نخواهیم داشت، بنابراین باید مطمئن شویم که نمونه‌گر همگرا شده است. یک چک استاندارد Gelman-روبین است \(\hat{R}\) آمار، که نیاز به زنجیره نمونه های متعدد. \(\hat{R}\) اقدامات درجه ای که واریانس (از آن) بین زنجیره های بیش از آنچه که انتظار می رود در صورتی که زنجیره توزیع یکسان شد. ارزش های \(\hat{R}\) نزدیک به 1 استفاده می شود برای نشان همگرایی تقریبی است. مشاهده منبع برای جزئیات بیشتر.

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0038308 1.0005717]
 [1.0005717 1.0006068]]

نقد مدل

اگر ما یک راه حل تحلیلی نداشتیم، اکنون زمان آن است که برخی از مدل های واقعی را نقد کنیم.

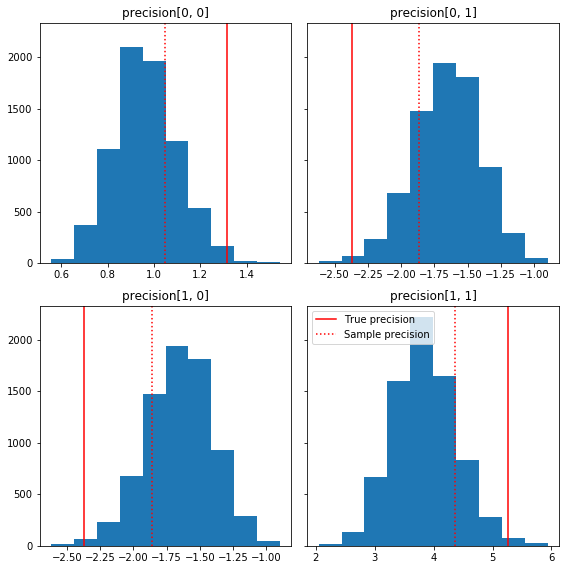
در اینجا چند هیستوگرام سریع از اجزای نمونه نسبت به حقیقت زمین ما (به رنگ قرمز) آورده شده است. توجه داشته باشید که نمونه ها از مقادیر ماتریس دقیق نمونه به سمت ماتریس هویت قبلی کوچک شده اند.

fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    ax.hist(precision_samples_reshaped[:, i, j])
    ax.axvline(true_precision[i, j], color='red',
               label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':',
               label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()

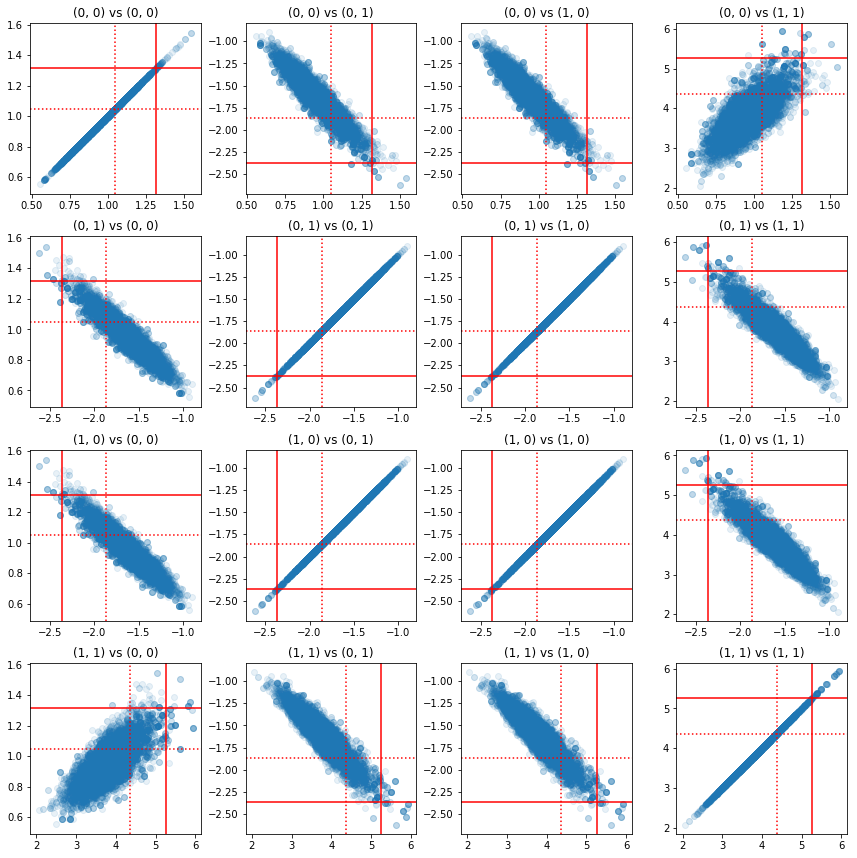
برخی از نمودارهای پراکنده از جفت مولفه های دقیق نشان می دهد که به دلیل ساختار همبستگی خلفی، مقادیر واقعی خلفی آنقدر که از حاشیه های بالا به نظر می رسد بعید نیستند.

fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
  for j1 in range(2):
    index1 = 2 * i1 + j1
    for i2 in range(2):
      for j2 in range(2):
        index2 = 2 * i2 + j2
        ax = axes[index1, index2]
        ax.scatter(precision_samples_reshaped[:, i1, j1],
                   precision_samples_reshaped[:, i2, j2], alpha=0.1)
        ax.axvline(true_precision[i1, j1], color='red')
        ax.axhline(true_precision[i2, j2], color='red')
        ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
        ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
        ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()

نسخه 4: نمونه برداری ساده تر از پارامترهای محدود

Bijectors نمونه‌برداری از ماتریس دقیق را ساده می‌کردند، اما مقدار مناسبی از تبدیل دستی به و از نمایش بدون محدودیت وجود داشت. یک راه ساده تر وجود دارد!

TransformedTransitionKernel

TransformedTransitionKernel ساده این فرایند است. نمونه‌گر شما را می‌پیچد و همه تبدیل‌ها را مدیریت می‌کند. به عنوان آرگومان، فهرستی از بیژکتورها را می گیرد که مقادیر پارامترهای نامحدود را به مقادیر محدود ترسیم می کند. بنابراین در اینجا ما نیاز به معکوس کردن precision_to_unconstrained bijector ما در بالا استفاده می شود. ما فقط می تواند استفاده tfb.Invert(precision_to_unconstrained) ، اما که شامل گرفتن از وارون وارون (TensorFlow است به اندازه کافی هوشمند به ساده نیست tf.Invert(tf.Invert()) به tf.Identity()) ، به طوری که به جای ما فقط یک بیژکتور جدید خواهم نوشت.

بیژکتور محدود کننده

# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
    # step 3: take the product of Cholesky factors
    tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: map a vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()

print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)

m:
 [[1.0, 2.0], [2.0, 8.0]]
unconstrained_to_precision.inverse(m):
 [0.6931472 2.        0.       ]
forward(unconstrained_to_precision.inverse(m)):
 [[1. 2.]
 [2. 8.]]

نمونه برداری با TransformedTransitionKernel

با TransformedTransitionKernel ، ما دیگر لازم نیست برای انجام تحولات دستی پارامترهای ما است. مقادیر اولیه و نمونه های ما همه ماتریس های دقیق هستند. ما فقط باید بایژکتور(های) نامحدود خود را به هسته انتقال دهیم و تمام تحولات را انجام می دهد.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  return states

precision_samples  = sample()

بررسی همگرایی

\(\hat{R}\) چک همگرایی نظر می رسد خوب!

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013582 1.0019467]
 [1.0019467 1.0011805]]

مقایسه در مقابل تحلیلی خلفی

مجدداً بیایید در مقابل تحلیلی پسین بررسی کنیم.

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96687526 -1.6552585 ]
 [-1.6552585   3.867676  ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329624 0.24913791]
 [0.24913791 0.53983927]]

بهینه سازی ها

اکنون که کارها را به صورت سرتاسر اجرا می کنیم، بیایید یک نسخه بهینه تر را انجام دهیم. سرعت برای این مثال خیلی مهم نیست، اما زمانی که ماتریس ها بزرگتر شوند، چند بهینه سازی تفاوت بزرگی ایجاد خواهد کرد.

یکی از پیشرفت‌های بزرگ سرعتی که می‌توانیم انجام دهیم، پارامترسازی مجدد از نظر تجزیه Cholesky است. دلیل این امر این است که تابع احتمال داده ما به هر دو ماتریس کوواریانس و دقت نیاز دارد. ماتریس معکوس گران قیمت (است\(O(n^3)\) برای \(n \times n\) ماتریس)، و اگر ما در شرایط از هر دو کوواریانس یا ماتریس دقت پارامترها، ما نیاز به انجام یک وارونگی برای دریافت دیگر.

به عنوان یک یادآوری، واقعی، مثبت قطعی، متقارن ماتریس \(M\) را می توان به یک محصول از فرم تجزیه \(M = L L^T\) که در آن ماتریس \(L\) مثلثی پایین است و دارای قطر مثبت است. با توجه به تجزیه Cholesky از \(M\)، ما موثر تر می تواند هر دو دست آوردن \(M\) (محصول یک پایین تر و یک ماتریس مثلثی بالا) و \(M^{-1}\) (از طریق تماس جانشینی). محاسبه فاکتورسازی Cholesky به خودی خود ارزان نیست، اما اگر از نظر عوامل Cholesky پارامتر کنیم، فقط باید فاکتورسازی Cholesky مقادیر پارامتر اولیه را محاسبه کنیم.

با استفاده از تجزیه کولسکی ماتریس کوواریانس

بهره وری کل عوامل دارای یک نسخه از توزیع نرمال چند متغیره، MultivariateNormalTriL است، که از نظر عامل Cholesky از کواریانس ماتریس پارامتر. بنابراین اگر بخواهیم بر حسب عامل Cholesky ماتریس کوواریانس پارامتر کنیم، می‌توانیم احتمال ثبت داده‌ها را به طور موثر محاسبه کنیم. چالش در محاسبه احتمال گزارش قبلی با کارایی مشابه است.

اگر نسخه‌ای از توزیع معکوس Wishart داشتیم که با فاکتورهای Cholesky نمونه‌ها کار می‌کرد، همه چیز آماده بود. افسوس که نداریم. (هر چند تیم از ارسال کد استقبال می کند!) به عنوان یک جایگزین، می توانیم از نسخه ای از توزیع Wishart استفاده کنیم که با فاکتورهای Cholesky نمونه ها همراه با زنجیره ای از بیژکتورها کار می کند.

در حال حاضر، ما برای اینکه کارها را واقعاً کارآمد کنیم، چند دستگاه بیژکتور را از دست داده‌ایم، اما من می‌خواهم این فرآیند را به عنوان تمرین و تصویر مفیدی از قدرت بیژکتورهای TFP نشان دهم.

توزیع Wishart که بر اساس عوامل Cholesky عمل می کند

Wishart توزیع دارای یک پرچم مفید، input_output_cholesky ، که مشخص می کند که ورودی و خروجی ماتریس باید عوامل Cholesky باشد. کار با فاکتورهای Cholesky نسبت به ماتریس های کامل کارآمدتر و از نظر عددی سودمندتر است، به همین دلیل این امر مطلوب است. یک نکته مهم در مورد معناشناسی پرچم: تنها نشانه ای که نمایندگی از ورودی و خروجی به توزیع باید تغییر است - آن را یک reparameterization کامل از توزیع، که یک اصلاح ژاکوبین به شامل نشان نمی دهد log_prob() عملکرد. ما در واقع می خواهیم این پارامترسازی مجدد کامل را انجام دهیم، بنابراین توزیع خود را خواهیم ساخت.

# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices.  Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).

class CholeskyWishart(tfd.TransformedDistribution):
  """Wishart distribution reparameterized to use Cholesky factors."""
  def __init__(self,
      df,
      scale_tril,
      validate_args=False,
      allow_nan_stats=True,
      name='CholeskyWishart'):
    # Wishart has a bunch of methods that we want to support but not
    # implement.  We'll subclass TransformedDistribution here to take care of
    # those.  We'll override the few for which speed is critical and implement
    # them with a separate Wishart for which input_output_cholesky=True
    super(CholeskyWishart, self).__init__(
        distribution=tfd.WishartTriL(
            df=df,
            scale_tril=scale_tril,
            input_output_cholesky=False,
            validate_args=validate_args,
            allow_nan_stats=allow_nan_stats),
        bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
        validate_args=validate_args,
        name=name
    )
    # Here's the Cholesky distribution we'll use for log_prob() and sample()
    self.cholesky = tfd.WishartTriL(
        df=df,
        scale_tril=scale_tril,
        input_output_cholesky=True,
        validate_args=validate_args,
        allow_nan_stats=allow_nan_stats)

  def _log_prob(self, x):
    return (self.cholesky.log_prob(x) +
            self.bijector.inverse_log_det_jacobian(x, event_ndims=2))

  def _sample_n(self, n, seed=None):
    return self.cholesky._sample_n(n, seed)

# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

@tf.function(autograph=False)
def compute_log_prob(m):
  w_transformed = tfd.TransformedDistribution(
      tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
      bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
  w_optimized = CholeskyWishart(
      df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
  log_prob_transformed = w_transformed.log_prob(m)
  log_prob_optimized = w_optimized.log_prob(m)
  return log_prob_transformed, log_prob_optimized

for matrix in [np.eye(2, dtype=np.float32),
               np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
  log_prob_transformed, log_prob_optimized = [
      t.numpy() for t in compute_log_prob(matrix)]
  print('Transformed Wishart:', log_prob_transformed)
  print('Optimized Wishart', log_prob_optimized)

Transformed Wishart: -0.84889317
Optimized Wishart -0.84889317
Transformed Wishart: -99.269455
Optimized Wishart -99.269455

ساخت یک توزیع Wishart معکوس

در حال حاضر ما کوواریانس ماتریس \(C\) تجزیه به \(C = L L^T\) که در آن \(L\) مثلثی پایین تر است و دارای یک قطر مثبت است. ما می خواهیم بدانیم احتمال \(L\) با توجه به اینکه \(C \sim W^{-1}(\nu, V)\) که در آن \(W^{-1}\) است که معکوس توزیع Wishart.

معکوس توزیع Wishart دارای خاصیت است که اگر \(C \sim W^{-1}(\nu, V)\)، سپس ماتریس دقت \(C^{-1} \sim W(\nu, V^{-1})\). بنابراین ما می توانیم احتمال گرفتن \(L\) از طریق یک TransformedDistribution که طول می کشد به عنوان پارامترهای توزیع Wishart و یک bijector که به یک عامل Cholesky معکوس آن نقشه عامل Cholesky ماتریس دقت.

یک راه ساده (اما فوق العاده کارآمد نیست) به از عامل Cholesky از دریافت \(C^{-1}\) به \(L\) است برای معکوس عامل Cholesky توسط تماس حل، پس از آن تشکیل ماتریس کواریانس از این عوامل معکوس، و سپس انجام یک فاکتور Cholesky .

اجازه دهید که تجزیه Cholesky از \(C^{-1} = M M^T\). \(M\) مثلثی پایین تر است، بنابراین ما می توانیم آن را با استفاده از معکوس MatrixInverseTriL bijector.

تشکیل \(C\) از \(M^{-1}\) : کمی مشکل است \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) مثلثی پایین تر است، بنابراین \(M^{-1}\) نیز مثلثی کمتر خواهد بود، و \(M^{-T}\) خواهد مثلثی بالا. CholeskyOuterProduct() bijector تنها با ماتریس مثلثی پایین کار می کند، بنابراین ما می توانیم آن را به فرم استفاده نکنید \(C\) از \(M^{-T}\). راه حل ما زنجیره ای از بیژکتورها است که سطرها و ستون های یک ماتریس را تغییر می دهند.

خوشبختانه این منطق در محصور CholeskyToInvCholesky bijector!

ترکیب تمام قطعات

# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()

print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)

numpy =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]
bijector =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]

توزیع نهایی ما

Wishart معکوس ما بر روی عوامل Cholesky به شرح زیر است:

inverse_wishart_cholesky = tfd.TransformedDistribution(
    distribution=CholeskyWishart(
        df=PRIOR_DF,
        scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
    bijector=tfb.CholeskyToInvCholesky())

ما Wishart معکوس خود را داریم، اما به نوعی کند است زیرا باید تجزیه Cholesky را در bijector انجام دهیم. بیایید به پارامترسازی ماتریس دقیق برگردیم و ببینیم در آنجا برای بهینه‌سازی چه کارهایی می‌توانیم انجام دهیم.

نسخه نهایی (!): با استفاده از تجزیه Cholesky ماتریس دقیق

یک رویکرد جایگزین کار با عوامل Cholesky ماتریس دقیق است. در اینجا تابع درستنمایی قبلی به راحتی قابل محاسبه است، اما تابع درستنمایی گزارش داده کار بیشتری می طلبد زیرا TFP نسخه ای از نرمال چند متغیره را ندارد که با دقت پارامترگذاری شود.

احتمال ورود به سیستم قبلی بهینه شده است

ما با استفاده از CholeskyWishart توزیع که در بالا ساخته شده است برای ساخت قبل.

# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

def log_lik_prior_cholesky(precisions_cholesky):
  rv_precision = CholeskyWishart(
      df=PRIOR_DF,
      scale_tril=PRIOR_SCALE_CHOLESKY,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions_cholesky)

# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
              true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
    distribution=tfd.WishartTriL(
        df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
    bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
    precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
    precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow slow:', lik_tf_slow[i])
  print('tensorflow fast:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow slow: -0.84889317
tensorflow fast: -0.84889317
1
numpy: -7.442875031036973
tensorflow slow: -7.442877
tensorflow fast: -7.442876

احتمال ثبت اطلاعات بهینه شده

We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:

Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)

Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)

Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.

Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now

\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)

So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).

Our approach (courtesy of this notebook ):

1. Use tfd.Independent() to combine a batch of 1-D Normal random variables into a single multi-dimensional random variable. The reinterpreted_batch_ndims parameter for Independent() specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, so reinterpreted_batch_ndims=1 .
2. Apply a bijector to add the desired covariance: tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)) . Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). The tfb.Invert takes care of inverting \(B\), and the adjoint=True flag performs the transpose.
3. Apply a bijector to add the desired offset: tfb.Shift(shift=shift) Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).

class MVNPrecisionCholesky(tfd.TransformedDistribution):
  """Multivariate normal parameterized by loc and Cholesky precision matrix."""

  def __init__(self, loc, precision_cholesky, name=None):
    super(MVNPrecisionCholesky, self).__init__(
        distribution=tfd.Independent(
            tfd.Normal(loc=tf.zeros_like(loc),
                       scale=tf.ones_like(loc)),
            reinterpreted_batch_ndims=1),
        bijector=tfb.Chain([
            tfb.Shift(shift=loc),
            tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
                                  adjoint=True)),
        ]),
        name=name)

@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
  n = tf.shape(precisions_cholesky)[0]  # number of precision matrices
  rv_data = MVNPrecisionCholesky(
      loc=tf.zeros([n, 2]),
      precision_cholesky=precisions_cholesky)
  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.81824

Combined log likelihood function

Now we combine our prior and data log likelihood functions in a closure.

def get_log_lik_cholesky(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_cholesky(precisions_cholesky):
    return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
            log_lik_prior_cholesky(precisions_cholesky))

  return _log_lik_cholesky

Constraining bijector

Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.

unconstrained_to_precision_cholesky = tfb.Chain([
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: expand the vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)

precisions_cholesky:
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

inv:
 [[ 0.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 3.5762781e-07 -2.0647411e+00  1.3721828e-01]]

fwd(inv):
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

Initial values

We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values_cholesky = []
for i in range(N_CHAINS):
  initial_values_cholesky.append(np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)

Sampling

We sample N_CHAINS chains using the TransformedTransitionKernel .

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_cholesky(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  samples = tf.linalg.matmul(states, states, transpose_b=True)
  return samples

precision_samples = sample()

Convergence check

A quick convergence check looks good:

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013583 1.0019467]
 [1.0019467 1.0011804]]

Comparing results to the analytic posterior

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])

And again, the sample means and standard deviations match those of the analytic posterior.

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.9668749 -1.6552604]
 [-1.6552604  3.8676758]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329637 0.24913797]
 [0.24913797 0.53983945]]

Ok, all done! We've got our optimized sampler working.