 Veja no TensorFlow.org Veja no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Este tutorial é uma introdução à previsão de séries temporais usando o TensorFlow. Ele constrói alguns estilos diferentes de modelos, incluindo Redes Neurais Convolucionais e Recorrentes (CNNs e RNNs).
Isso é coberto em duas partes principais, com subseções:
- Previsão para uma única etapa de tempo:
- Um único recurso.
- Todos os recursos.
- Prever várias etapas:
- Single-shot: Faça as previsões de uma só vez.
- Autoregressivo: Faça uma previsão de cada vez e envie a saída de volta ao modelo.
Configurar
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
O conjunto de dados meteorológicos
Este tutorial usa um conjunto de dados de séries temporais de clima registrado pelo Instituto Max Planck de Biogeoquímica .
Este conjunto de dados contém 14 recursos diferentes, como temperatura do ar, pressão atmosférica e umidade. Estes foram coletados a cada 10 minutos, a partir de 2003. Para eficiência, você usará apenas os dados coletados entre 2009 e 2016. Esta seção do conjunto de dados foi preparada por François Chollet para seu livro Deep Learning with Python .
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
Este tutorial irá lidar apenas com previsões por hora , então comece por subamostrar os dados de intervalos de 10 minutos para intervalos de uma hora:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
Vamos dar uma olhada nos dados. Aqui estão as primeiras linhas:
df.head()
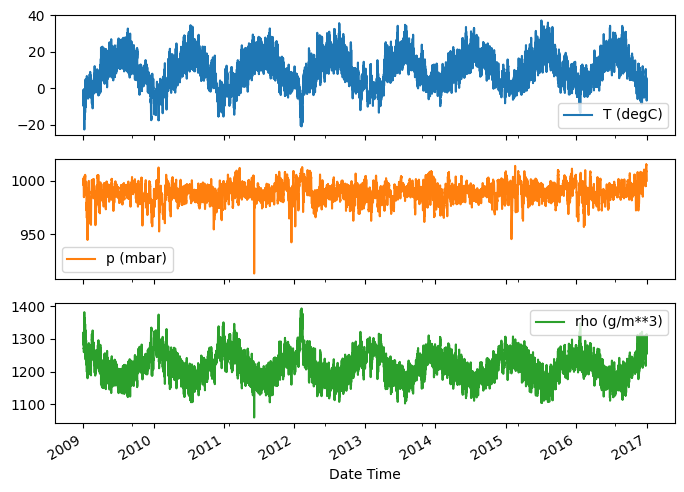
Aqui está a evolução de alguns recursos ao longo do tempo:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
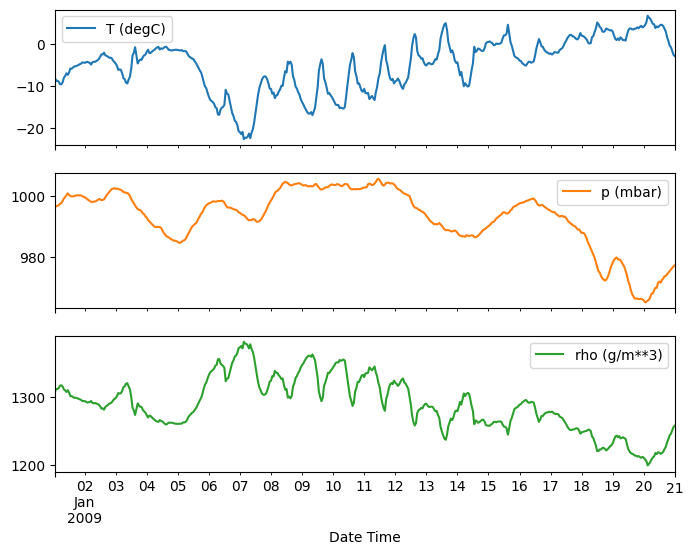
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
Inspecione e limpe
Em seguida, observe as estatísticas do conjunto de dados:
df.describe().transpose()
Velocidade do vento
Uma coisa que deve se destacar é o valor min das colunas de velocidade do vento ( wv (m/s) ) e o valor máximo ( max. wv (m/s) ). Este -9999 é provavelmente errôneo.
Há uma coluna de direção do vento separada, então a velocidade deve ser maior que zero ( >=0 ). Substitua por zeros:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
Engenharia de recursos
Antes de mergulhar na construção de um modelo, é importante entender seus dados e certificar-se de que você está transmitindo os dados formatados adequadamente.
Vento
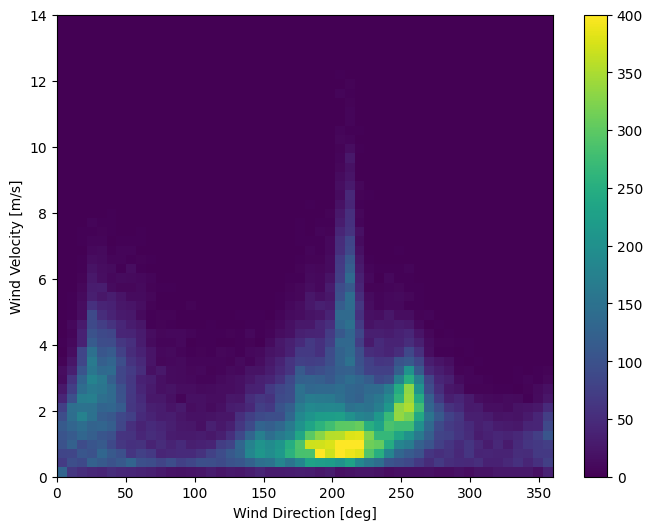
A última coluna dos dados, wd (deg) dá a direção do vento em unidades de graus. Os ângulos não são boas entradas de modelo: 360° e 0° devem estar próximos um do outro e envolver suavemente. A direção não deve importar se o vento não estiver soprando.
No momento, a distribuição dos dados de vento se parece com isso:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
Mas isso será mais fácil para o modelo interpretar se você converter as colunas de direção e velocidade do vento em um vetor de vento:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
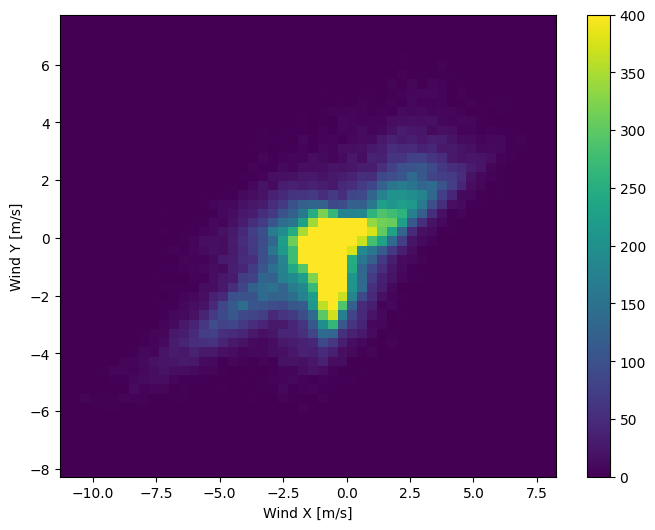
A distribuição dos vetores de vento é muito mais simples para o modelo interpretar corretamente:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
Tempo
Da mesma forma, a coluna Date Time é muito útil, mas não neste formato de string. Comece convertendo para segundos:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
Semelhante à direção do vento, o tempo em segundos não é uma entrada útil do modelo. Sendo dados meteorológicos, tem periodicidade diária e anual clara. Há muitas maneiras de lidar com a periodicidade.
Você pode obter sinais utilizáveis usando transformações de seno e cosseno para limpar os sinais de "Hora do dia" e "Hora do ano":
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
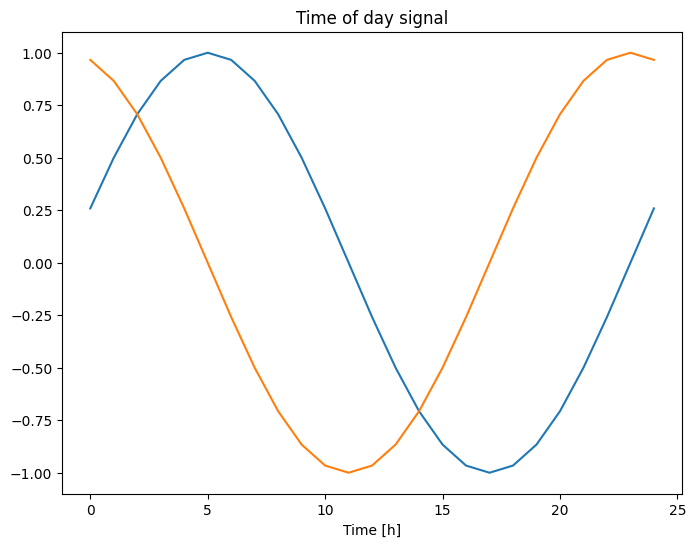
Isso dá ao modelo acesso aos recursos de frequência mais importantes. Nesse caso, você sabia de antemão quais frequências eram importantes.
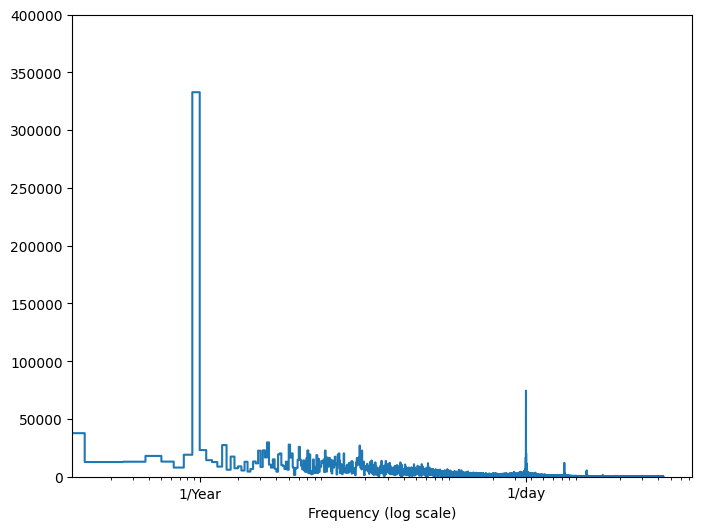
Se você não tiver essa informação, poderá determinar quais frequências são importantes extraindo recursos com Fast Fourier Transform . Para verificar as suposições, aqui está o tf.signal.rfft da temperatura ao longo do tempo. Observe os picos óbvios em frequências próximas a 1/year e 1/day :
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
Dividir os dados
Você usará uma divisão (70%, 20%, 10%) para os conjuntos de treinamento, validação e teste. Observe que os dados não estão sendo embaralhados aleatoriamente antes da divisão. Isso por dois motivos:
- Garante que ainda é possível cortar os dados em janelas de amostras consecutivas.
- Garante que os resultados da validação/teste sejam mais realistas, sendo avaliados nos dados coletados após o treinamento do modelo.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
Normalize os dados
É importante dimensionar recursos antes de treinar uma rede neural. A normalização é uma maneira comum de fazer essa escala: subtrair a média e dividir pelo desvio padrão de cada recurso.
A média e o desvio padrão só devem ser calculados usando os dados de treinamento para que os modelos não tenham acesso aos valores nos conjuntos de validação e teste.
Também é discutível que o modelo não deve ter acesso a valores futuros no conjunto de treinamento durante o treinamento e que essa normalização deve ser feita usando médias móveis. Esse não é o foco deste tutorial, e os conjuntos de validação e teste garantem que você obtenha métricas (um pouco) honestas. Portanto, no interesse da simplicidade, este tutorial usa uma média simples.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
Agora, dê uma olhada na distribuição dos recursos. Alguns recursos têm caudas longas, mas não há erros óbvios como o valor da velocidade do vento -9999 .
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

Janelas de dados
Os modelos neste tutorial farão um conjunto de previsões com base em uma janela de amostras consecutivas dos dados.
As principais características das janelas de entrada são:
- A largura (número de etapas de tempo) das janelas de entrada e rótulo.
- O deslocamento de tempo entre eles.
- Quais recursos são usados como entradas, rótulos ou ambos.
Este tutorial cria uma variedade de modelos (incluindo modelos Linear, DNN, CNN e RNN) e os usa para ambos:
- Previsões de saída única e várias saídas .
- Previsões de um passo de tempo e de vários passos de tempo .
Esta seção se concentra na implementação da janela de dados para que ela possa ser reutilizada para todos esses modelos.
Dependendo da tarefa e do tipo de modelo, você pode querer gerar uma variedade de janelas de dados. aqui estão alguns exemplos:
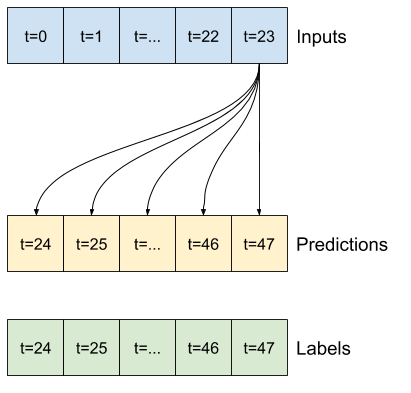
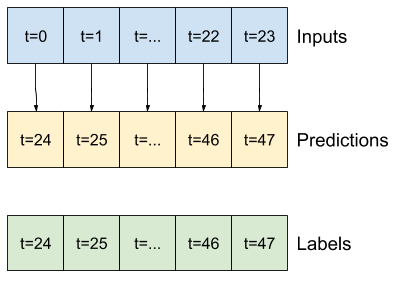
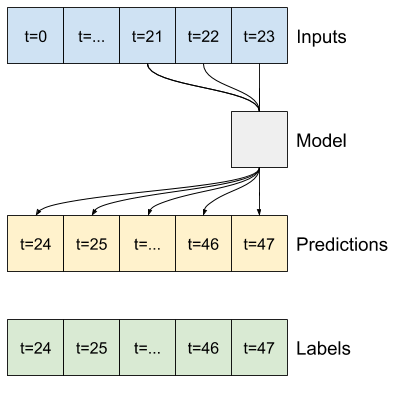
Por exemplo, para fazer uma única previsão 24 horas no futuro, com 24 horas de histórico, você pode definir uma janela como esta:
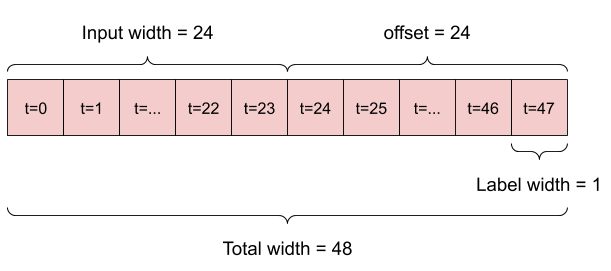
Um modelo que faz uma previsão para uma hora no futuro, com seis horas de histórico, precisaria de uma janela como esta:

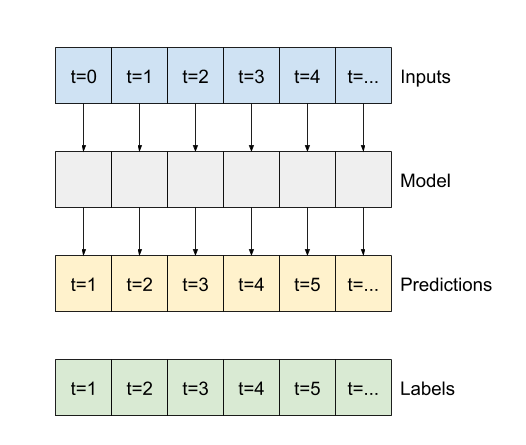
O restante desta seção define uma classe WindowGenerator . Esta classe pode:
- Manipule os índices e deslocamentos conforme mostrado nos diagramas acima.
- Divida janelas de recursos em pares
(features, labels). - Plote o conteúdo das janelas resultantes.
- Gere lotes dessas janelas com eficiência a partir dos dados de treinamento, avaliação e teste, usando
tf.data.Datasets.
1. Índices e deslocamentos
Comece criando a classe WindowGenerator . O método __init__ inclui toda a lógica necessária para os índices de entrada e rótulo.
Também leva o treinamento, avaliação e teste de DataFrames como entrada. Estes serão convertidos para tf.data.Dataset s de janelas posteriormente.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
Aqui está o código para criar as 2 janelas mostradas nos diagramas no início desta seção:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. Divisão
Dada uma lista de entradas consecutivas, o método split_window as converterá em uma janela de entradas e uma janela de rótulos.
O exemplo w2 que você definiu anteriormente será dividido assim:
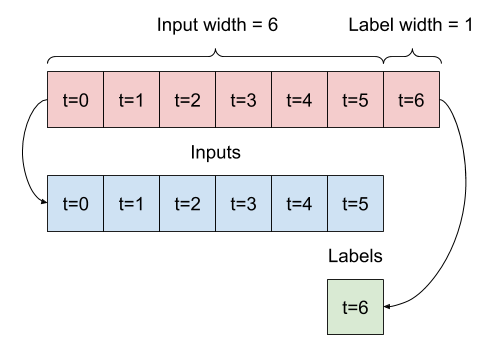
Este diagrama não mostra o eixo de features dos dados, mas essa função split_window também manipula o label_columns para que possa ser usado para exemplos de saída única e saída múltipla.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
Experimente:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
Normalmente, os dados no TensorFlow são empacotados em matrizes em que o índice mais externo está nos exemplos (a dimensão "lote"). Os índices intermediários são as dimensões de "tempo" ou "espaço" (largura, altura). Os índices mais internos são os recursos.
O código acima levou um lote de três janelas de 7 etapas de tempo com 19 recursos em cada etapa de tempo. Ele os divide em um lote de entradas de 19 recursos de 6 etapas e um rótulo de 1 recurso de etapa 1. O rótulo tem apenas um recurso porque o WindowGenerator foi inicializado com label_columns=['T (degC)'] . Inicialmente, este tutorial construirá modelos que prevêem rótulos de saída únicos.
3. Trama
Aqui está um método de plotagem que permite uma visualização simples da janela dividida:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
Este gráfico alinha entradas, rótulos e (posteriormente) previsões com base na hora a que o item se refere:
w2.plot()
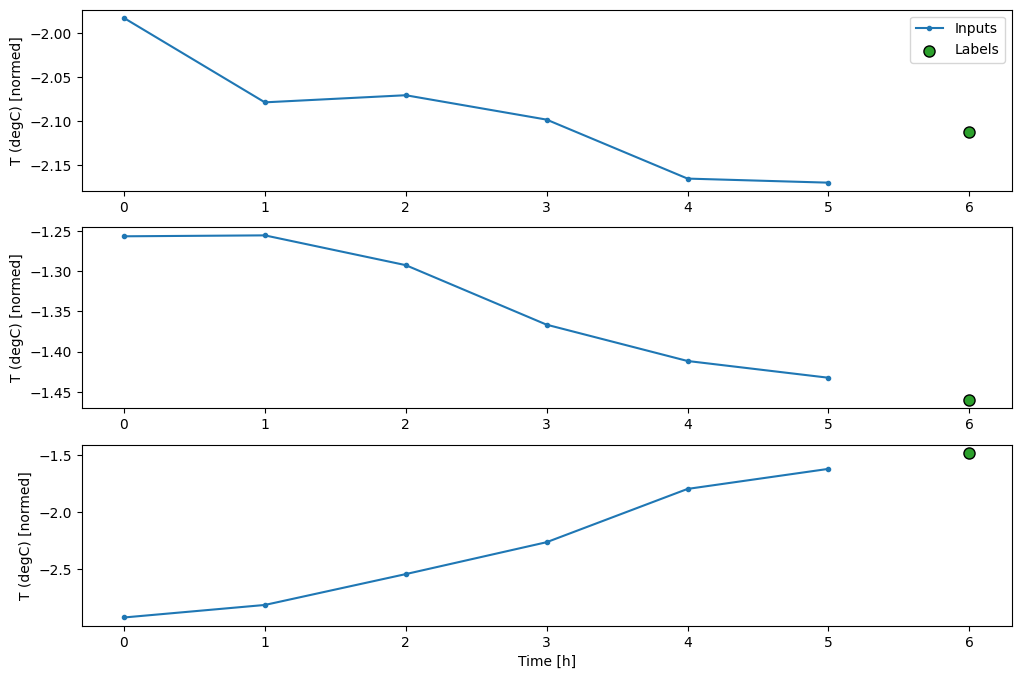
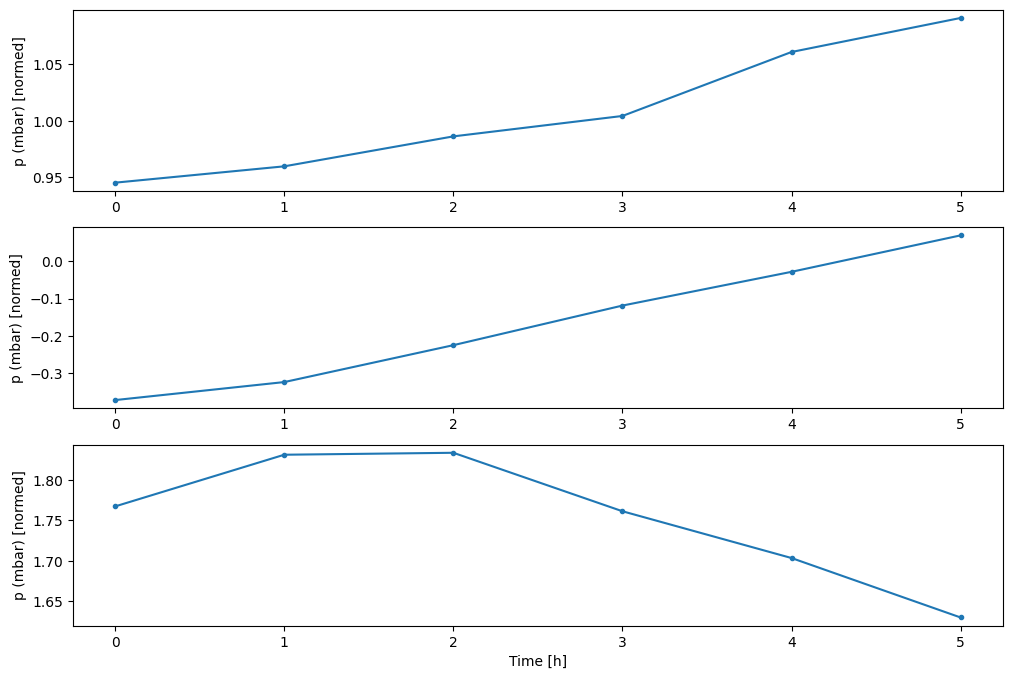
Você pode plotar as outras colunas, mas a configuração da janela de exemplo w2 só tem rótulos para a coluna T (degC) .
w2.plot(plot_col='p (mbar)')
4. Crie tf.data.Dataset s
Finalmente, este método make_dataset um DataFrame de série temporal e o converterá em um tf.data.Dataset de (input_window, label_window) usando a função tf.keras.utils.timeseries_dataset_from_array :
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
O objeto WindowGenerator contém dados de treinamento, validação e teste.
Adicione propriedades para acessá-los como tf.data.Dataset s usando o método make_dataset definido anteriormente. Além disso, adicione um lote de exemplo padrão para fácil acesso e plotagem:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
Agora, o objeto WindowGenerator fornece acesso aos objetos tf.data.Dataset , para que você possa iterar facilmente sobre os dados.
A propriedade Dataset.element_spec informa a estrutura, os tipos de dados e as formas dos elementos do conjunto de dados.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
A iteração em um conjunto de Dataset produz lotes concretos:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
Modelos de passo único
O modelo mais simples que você pode construir com esse tipo de dados é aquele que prevê o valor de um único recurso — 1 passo de tempo (uma hora) no futuro com base apenas nas condições atuais.
Portanto, comece construindo modelos para prever o valor de T (degC) uma hora no futuro.
Configure um objeto WindowGenerator para produzir esses pares de etapa única (input, label) :
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
O objeto window cria tf.data.Dataset s a partir dos conjuntos de treinamento, validação e teste, permitindo iterar facilmente em lotes de dados.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
Linha de base
Antes de construir um modelo treinável, seria bom ter uma linha de base de desempenho como ponto de comparação com os modelos posteriores mais complicados.
Esta primeira tarefa é prever a temperatura uma hora no futuro, dado o valor atual de todos os recursos. Os valores atuais incluem a temperatura atual.
Portanto, comece com um modelo que apenas retorne a temperatura atual como a previsão, prevendo "Sem alteração". Esta é uma linha de base razoável, pois a temperatura muda lentamente. Obviamente, essa linha de base funcionará menos bem se você fizer uma previsão mais adiante.
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
Instancie e avalie este modelo:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
Isso imprimiu algumas métricas de desempenho, mas elas não dão uma ideia de quão bem o modelo está se saindo.
O WindowGenerator tem um método de plotagem, mas os plots não serão muito interessantes com apenas uma amostra.
Portanto, crie um WindowGenerator mais amplo que gere janelas 24 horas de entradas e rótulos consecutivos por vez. A nova variável wide_window não altera a maneira como o modelo opera. O modelo ainda faz previsões uma hora no futuro com base em uma única etapa de tempo de entrada. Aqui, o eixo do time funciona como o eixo do batch : cada previsão é feita de forma independente, sem interação entre as etapas de tempo:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
Essa janela expandida pode ser passada diretamente para o mesmo modelo de baseline de base sem nenhuma alteração de código. Isso é possível porque as entradas e os rótulos têm o mesmo número de passos de tempo e a linha de base apenas encaminha a entrada para a saída:
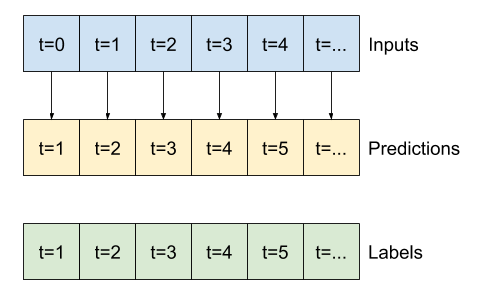
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
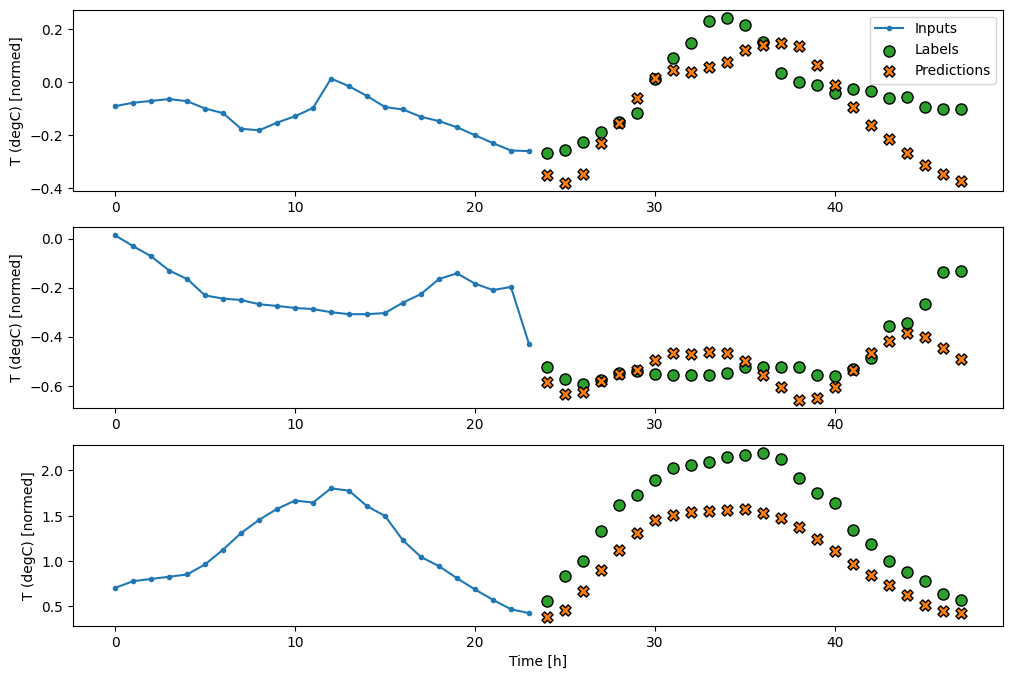
Ao plotar as previsões do modelo de linha de base, observe que são simplesmente os rótulos deslocados para a direita em uma hora:
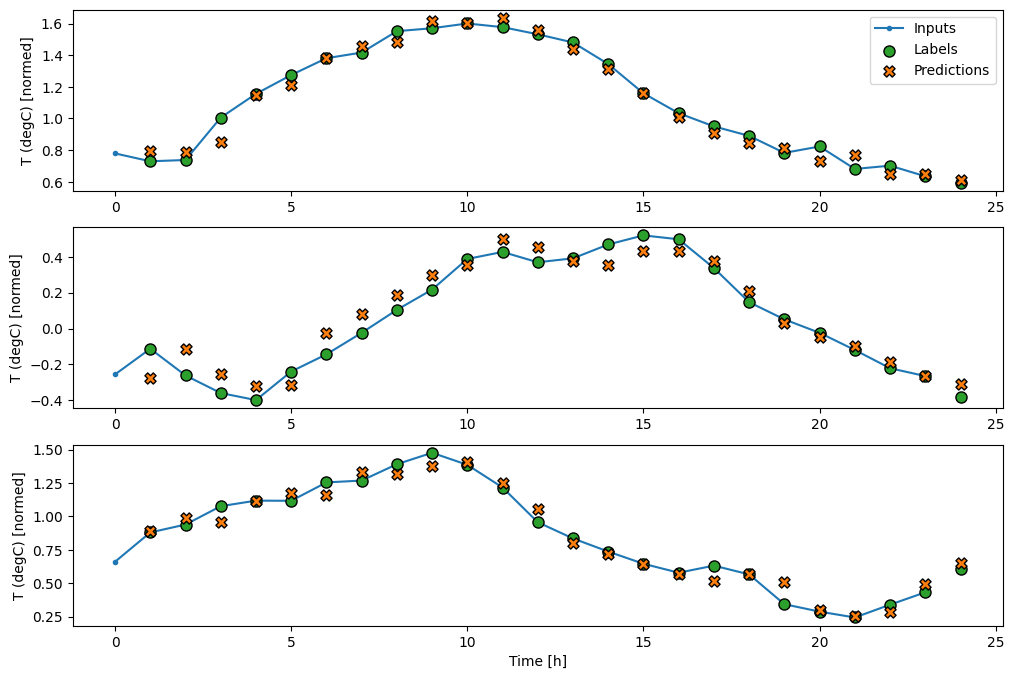
wide_window.plot(baseline)
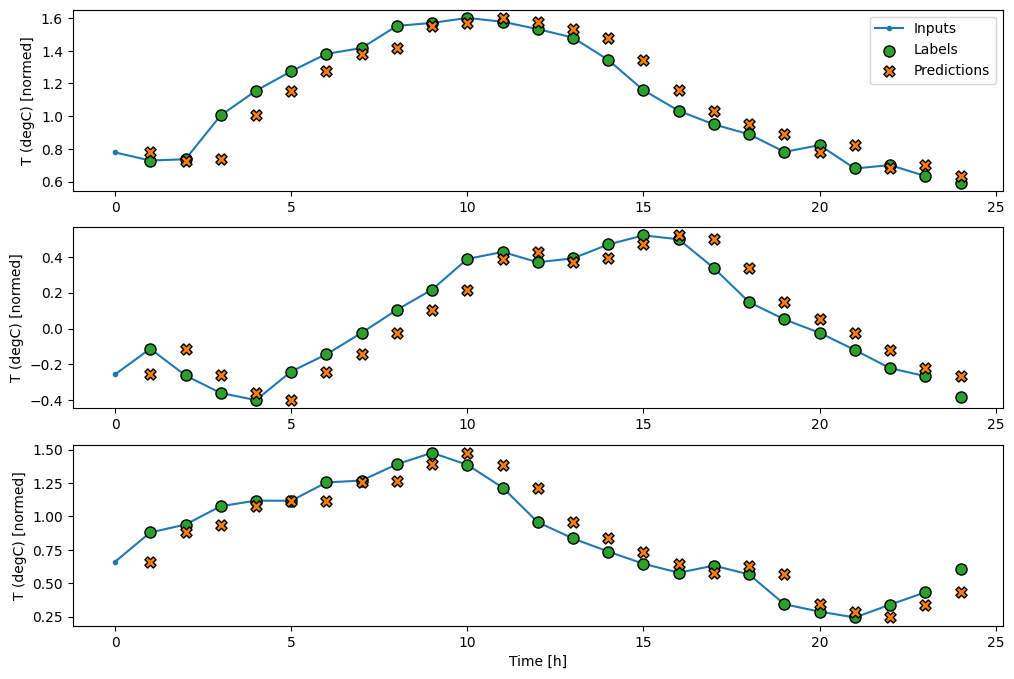
Nos gráficos acima de três exemplos, o modelo de etapa única é executado ao longo de 24 horas. Isso merece alguma explicação:
- A linha azul de
Inputsmostra a temperatura de entrada em cada passo de tempo. O modelo recebe todos os recursos, este gráfico mostra apenas a temperatura. - Os pontos verdes dos
Labelsmostram o valor da previsão de destino. Esses pontos são mostrados no tempo de previsão, não no tempo de entrada. É por isso que o intervalo de rótulos é deslocado 1 passo em relação às entradas. - Os cruzamentos de
Predictionslaranja são as previsões do modelo para cada passo de tempo de saída. Se o modelo estivesse prevendo perfeitamente, as previsões chegariam diretamente aosLabels.
Modelo linear
O modelo treinável mais simples que você pode aplicar a essa tarefa é inserir a transformação linear entre a entrada e a saída. Nesse caso, a saída de uma etapa de tempo depende apenas dessa etapa:

Uma camada tf.keras.layers.Dense sem conjunto de activation é um modelo linear. A camada apenas transforma o último eixo dos dados de (batch, time, inputs) para (batch, time, units) ; ele é aplicado independentemente a cada item nos eixos de batch e time .
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
Este tutorial treina muitos modelos, portanto, empacote o procedimento de treinamento em uma função:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
Treine o modelo e avalie seu desempenho:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
Assim como o modelo de linha de baseline , o modelo linear pode ser chamado em lotes de janelas amplas. Usado desta forma, o modelo faz um conjunto de previsões independentes em passos de tempo consecutivos. O eixo do time atua como outro eixo de batch . Não há interações entre as previsões em cada passo de tempo.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
Aqui está o gráfico de suas previsões de exemplo na wide_window , observe como em muitos casos a previsão é claramente melhor do que apenas retornar a temperatura de entrada, mas em alguns casos é pior:
wide_window.plot(linear)
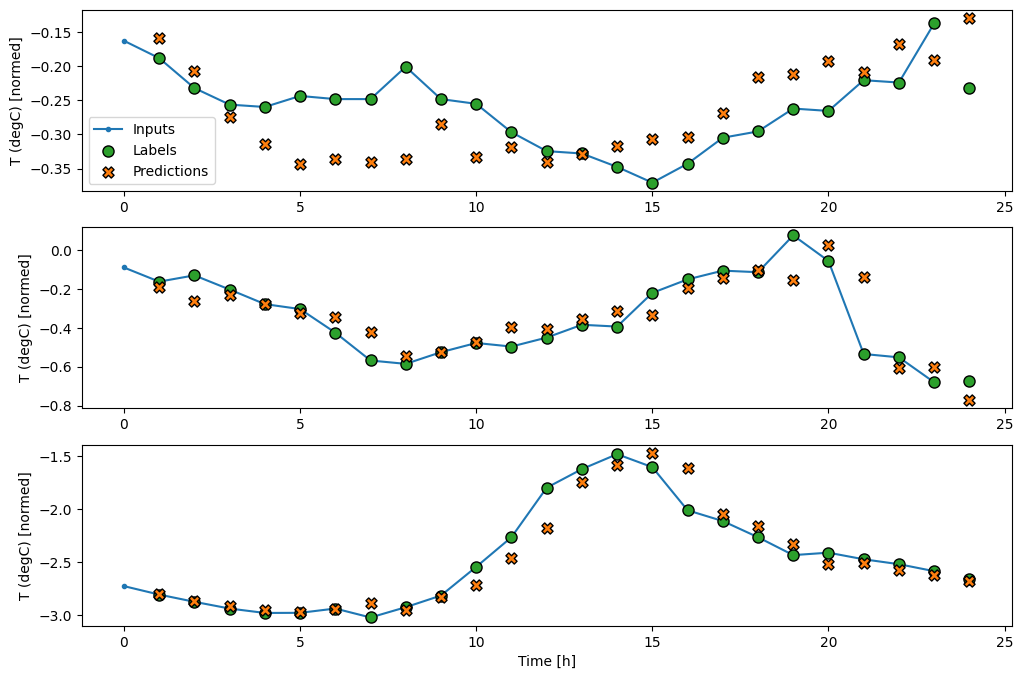
Uma vantagem dos modelos lineares é que eles são relativamente simples de interpretar. Você pode extrair os pesos da camada e visualizar o peso atribuído a cada entrada:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
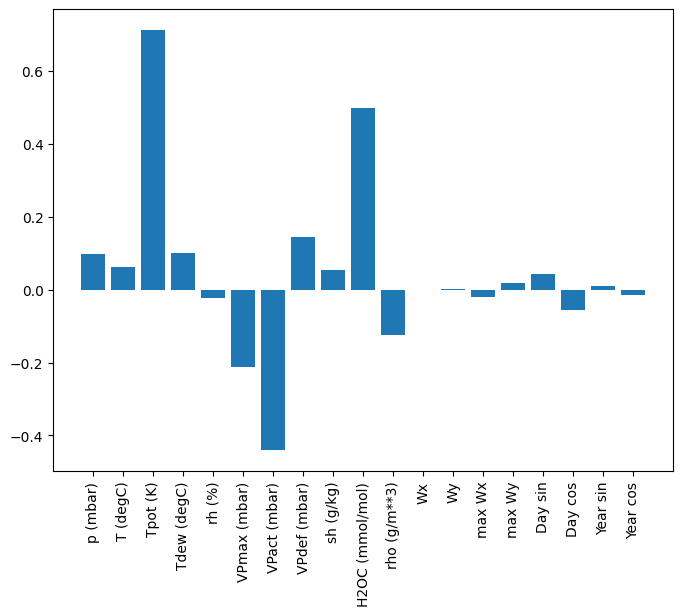
Às vezes o modelo nem coloca mais peso na entrada T (degC) . Este é um dos riscos da inicialização aleatória.
Denso
Antes de aplicar modelos que realmente operam em várias etapas de tempo, vale a pena verificar o desempenho de modelos de etapa de entrada única mais profundos e poderosos.
Aqui está um modelo semelhante ao modelo linear , exceto que empilha várias camadas Dense entre a entrada e a saída:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
Multi-passo denso
Um modelo de passo único não tem contexto para os valores atuais de suas entradas. Ele não pode ver como os recursos de entrada estão mudando ao longo do tempo. Para resolver esse problema, o modelo precisa acessar várias etapas de tempo ao fazer previsões:
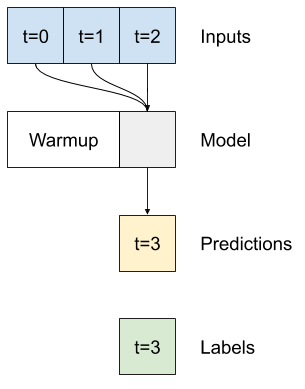
Os modelos de linha de baseline , linear e dense trataram cada passo de tempo de forma independente. Aqui, o modelo terá várias etapas de tempo como entrada para produzir uma única saída.
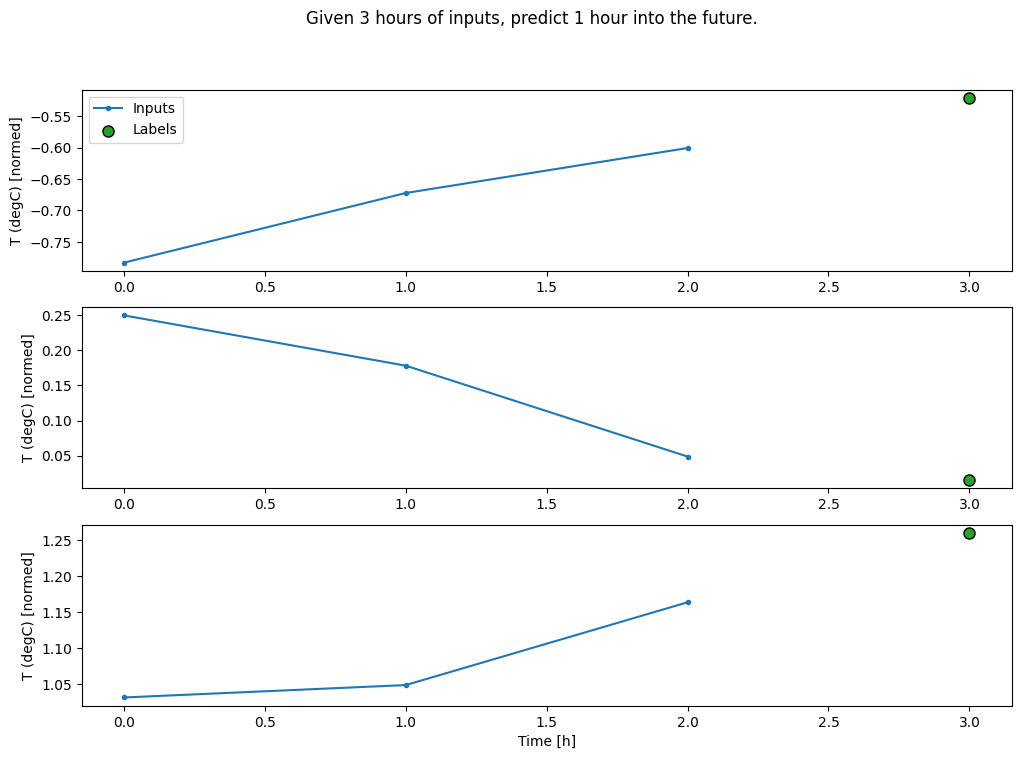
Crie um WindowGenerator que produzirá lotes de entradas de três horas e rótulos de uma hora:
Observe que o parâmetro shift da Window é relativo ao final das duas janelas.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
Você pode treinar um modelo dense em uma janela de várias etapas de entrada adicionando um tf.keras.layers.Flatten como a primeira camada do modelo:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
conv_window.plot(multi_step_dense)
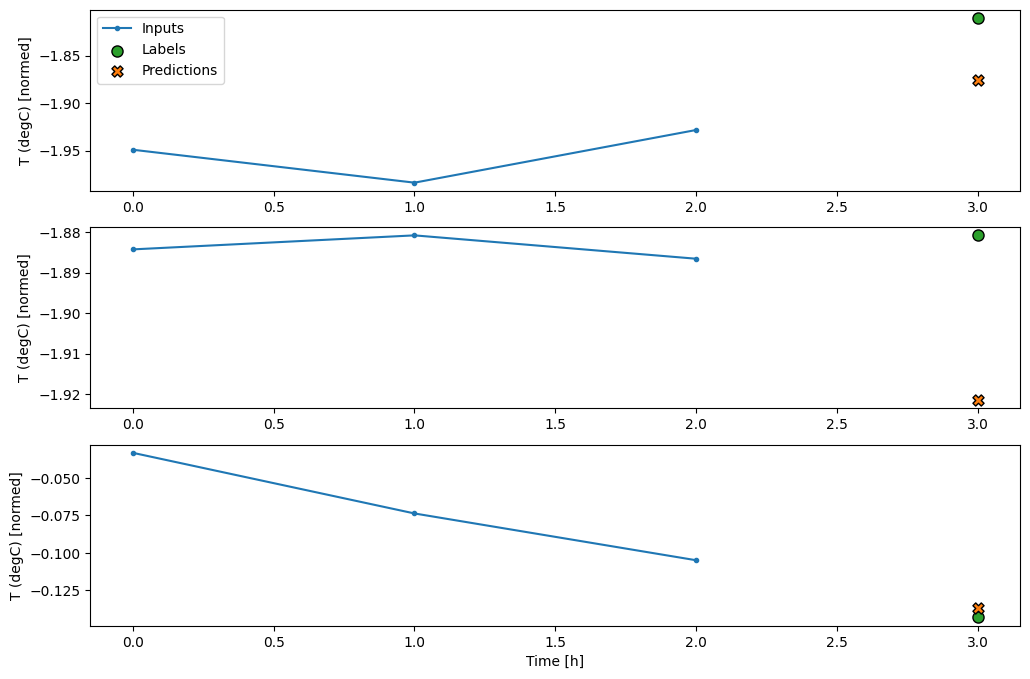
A principal desvantagem dessa abordagem é que o modelo resultante só pode ser executado em janelas de entrada exatamente dessa forma.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
Os modelos convolucionais na próxima seção corrigem esse problema.
Rede neural de convolução
Uma camada de convolução ( tf.keras.layers.Conv1D ) também usa várias etapas de tempo como entrada para cada previsão.
Abaixo está o mesmo modelo de multi_step_dense , reescrito com uma convolução.
Observe as mudanças:
- O
tf.keras.layers.Flattene o primeirotf.keras.layers.Densesão substituídos por umtf.keras.layers.Conv1D. - O
tf.keras.layers.Reshapenão é mais necessário, pois a convolução mantém o eixo do tempo em sua saída.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
Execute-o em um lote de exemplo para verificar se o modelo produz saídas com a forma esperada:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
Treine e avalie no conv_window e ele deve fornecer desempenho semelhante ao modelo multi_step_dense .
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
A diferença entre este conv_model e o modelo multi_step_dense é que o conv_model pode ser executado em entradas de qualquer tamanho. A camada convolucional é aplicada a uma janela deslizante de entradas:
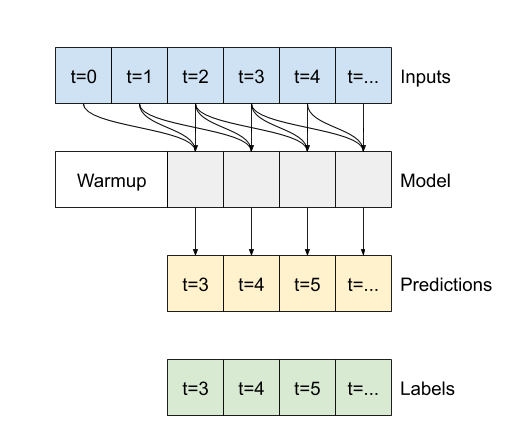
Se você executá-lo em uma entrada mais ampla, ele produzirá uma saída mais ampla:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
Observe que a saída é menor que a entrada. Para que o treinamento ou a plotagem funcionem, você precisa que os rótulos e a previsão tenham o mesmo comprimento. Portanto, construa um WindowGenerator para produzir janelas amplas com algumas etapas extras de tempo de entrada para que os comprimentos do rótulo e da previsão correspondam:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
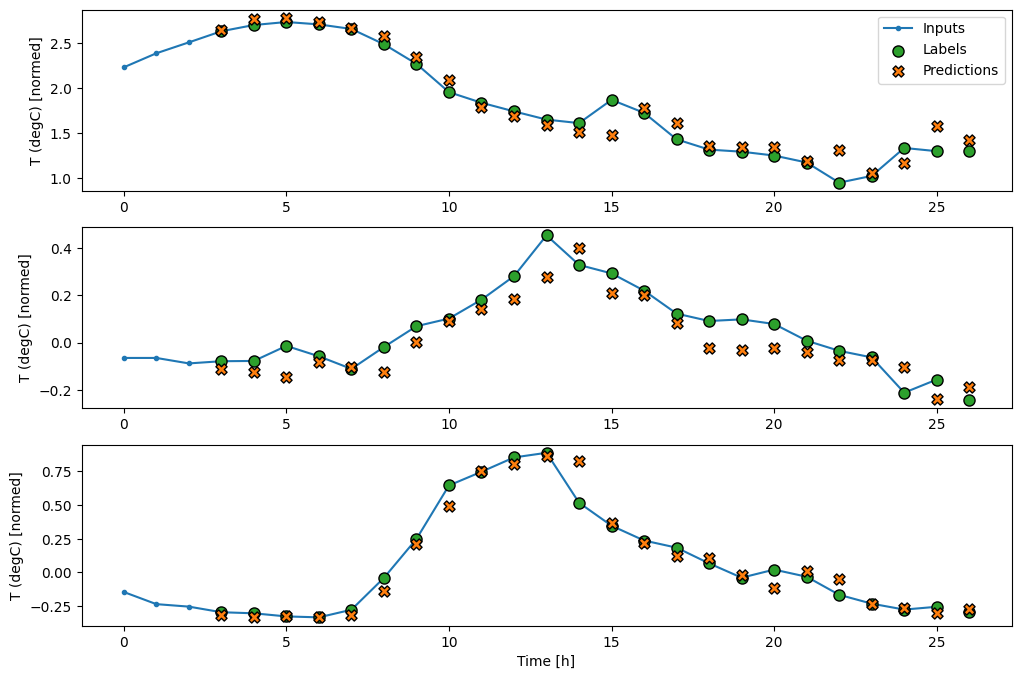
Agora, você pode plotar as previsões do modelo em uma janela mais ampla. Observe os 3 passos de tempo de entrada antes da primeira previsão. Cada previsão aqui é baseada nos 3 passos de tempo anteriores:
wide_conv_window.plot(conv_model)
Rede neural recorrente
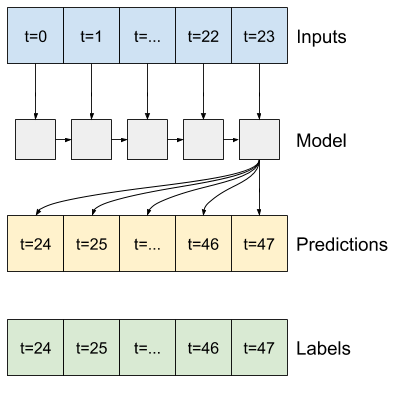
Uma Rede Neural Recorrente (RNN) é um tipo de rede neural adequada para dados de séries temporais. As RNNs processam uma série temporal passo a passo, mantendo um estado interno de passo a passo.
Você pode aprender mais na geração de texto com um tutorial RNN e no guia Redes neurais recorrentes (RNN) com Keras .
Neste tutorial, você usará uma camada RNN chamada Long Short-Term Memory ( tf.keras.layers.LSTM ).
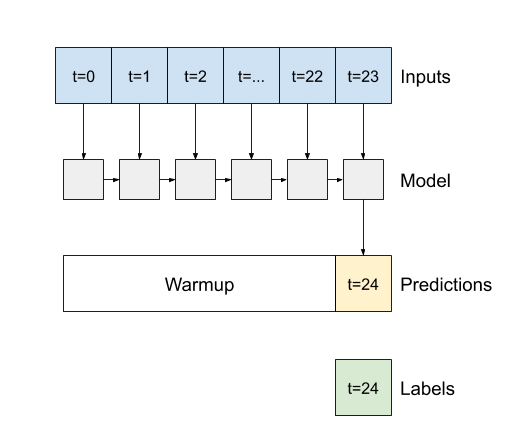
Um argumento construtor importante para todas as camadas Keras RNN, como tf.keras.layers.LSTM , é o argumento return_sequences . Essa configuração pode configurar a camada de duas maneiras:
- Se
False, o padrão, a camada retorna apenas a saída do passo de tempo final, dando ao modelo tempo para aquecer seu estado interno antes de fazer uma única previsão:
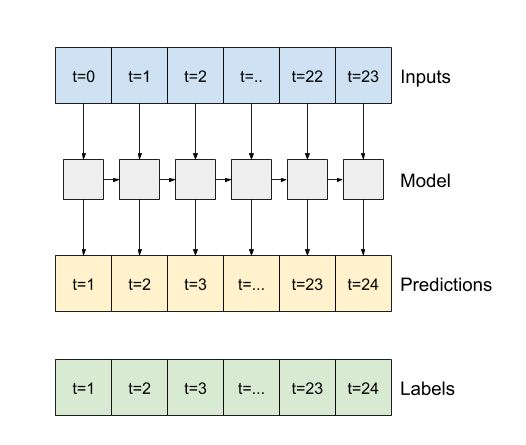
- Se
True, a camada retorna uma saída para cada entrada. Isso é útil para:- Empilhamento de camadas RNN.
- Treinar um modelo em várias etapas de tempo simultaneamente.
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
Com return_sequences=True , o modelo pode ser treinado em 24 horas de dados por vez.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
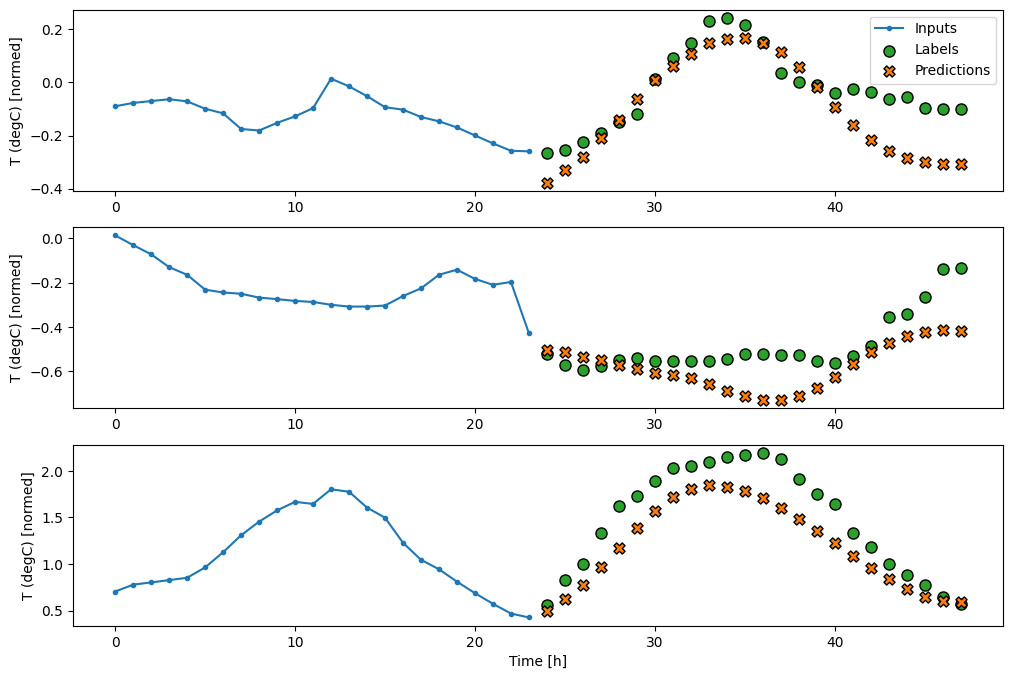
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
wide_window.plot(lstm_model)
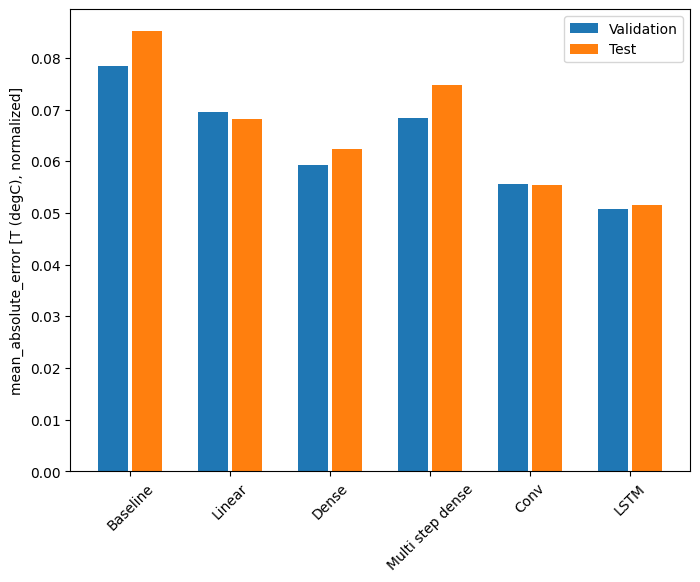
Desempenho
Com esse conjunto de dados, normalmente cada um dos modelos se sai um pouco melhor do que o anterior:
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()
for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
Modelos de várias saídas
Todos os modelos até agora previram uma única característica de saída, T (degC) , para um único passo de tempo.
Todos esses modelos podem ser convertidos para prever vários recursos apenas alterando o número de unidades na camada de saída e ajustando as janelas de treinamento para incluir todos os recursos nos labels ( example_labels ):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
Observe acima que o eixo de features dos rótulos agora tem a mesma profundidade que as entradas, em vez de 1 .
Linha de base
O mesmo modelo de linha de base ( Baseline ) pode ser usado aqui, mas desta vez repetindo todos os recursos em vez de selecionar um label_index específico:
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
Denso
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
RN
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
Avançado: conexões residuais
O modelo de Baseline de base anterior aproveitou o fato de que a sequência não muda drasticamente de um passo para outro. Cada modelo treinado neste tutorial até agora foi inicializado aleatoriamente e, em seguida, teve que aprender que a saída é uma pequena mudança em relação à etapa de tempo anterior.
Embora você possa contornar esse problema com uma inicialização cuidadosa, é mais simples construir isso na estrutura do modelo.
É comum na análise de séries temporais construir modelos que, em vez de prever o próximo valor, predizem como o valor mudará na próxima etapa de tempo. Da mesma forma, redes residuais — ou ResNets — em deep learning referem-se a arquiteturas em que cada camada contribui para o resultado acumulado do modelo.
É assim que você aproveita o conhecimento de que a mudança deve ser pequena.
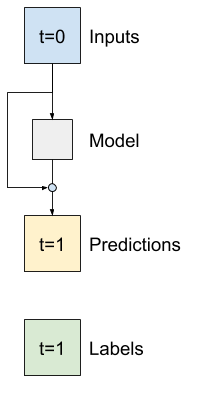
Essencialmente, isso inicializa o modelo para corresponder ao Baseline . Para esta tarefa, ajuda os modelos a convergir mais rapidamente, com desempenho ligeiramente melhor.
Essa abordagem pode ser usada em conjunto com qualquer modelo discutido neste tutorial.
Aqui, ele está sendo aplicado ao modelo LSTM, observe o uso do tf.initializers.zeros para garantir que as mudanças iniciais previstas sejam pequenas e não sobrecarreguem a conexão residual. Não há preocupações de quebra de simetria para os gradientes aqui, pois os zeros são usados apenas na última camada.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
Desempenho
Aqui está o desempenho geral para esses modelos de várias saídas.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
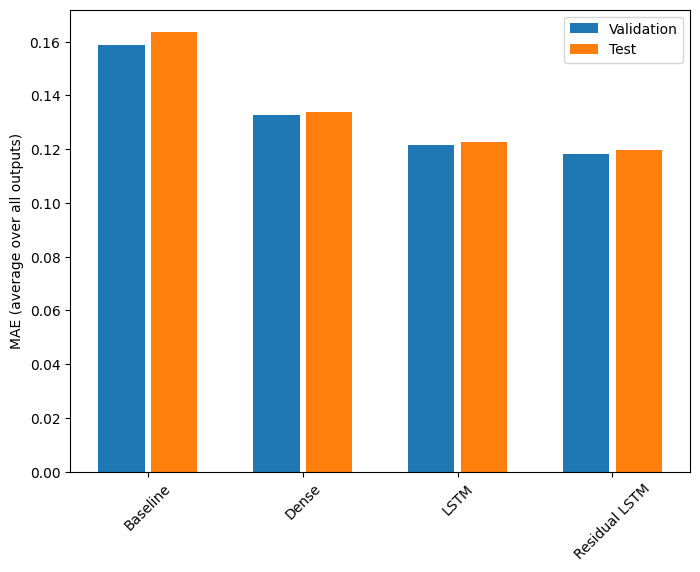
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
Os desempenhos acima são calculados em média em todas as saídas do modelo.
Modelos de várias etapas
Os modelos de saída única e saída múltipla nas seções anteriores fizeram previsões de etapa de tempo única , uma hora no futuro.
Esta seção mostra como expandir esses modelos para fazer previsões de várias etapas de tempo .
Em uma previsão de várias etapas, o modelo precisa aprender a prever uma faixa de valores futuros. Assim, ao contrário de um modelo de etapa única, onde apenas um único ponto futuro é previsto, um modelo de várias etapas prevê uma sequência de valores futuros.
Existem duas abordagens aproximadas para isso:
- Previsões de disparo único em que toda a série temporal é prevista de uma só vez.
- Previsões autorregressivas em que o modelo faz apenas previsões de etapa única e sua saída é realimentada como entrada.
Nesta seção, todos os modelos irão prever todos os recursos em todas as etapas de tempo de saída .
Para o modelo de várias etapas, os dados de treinamento consistem novamente em amostras horárias. No entanto, aqui, os modelos aprenderão a prever 24 horas no futuro, considerando 24 horas do passado.
Aqui está um objeto Window que gera essas fatias do conjunto de dados:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
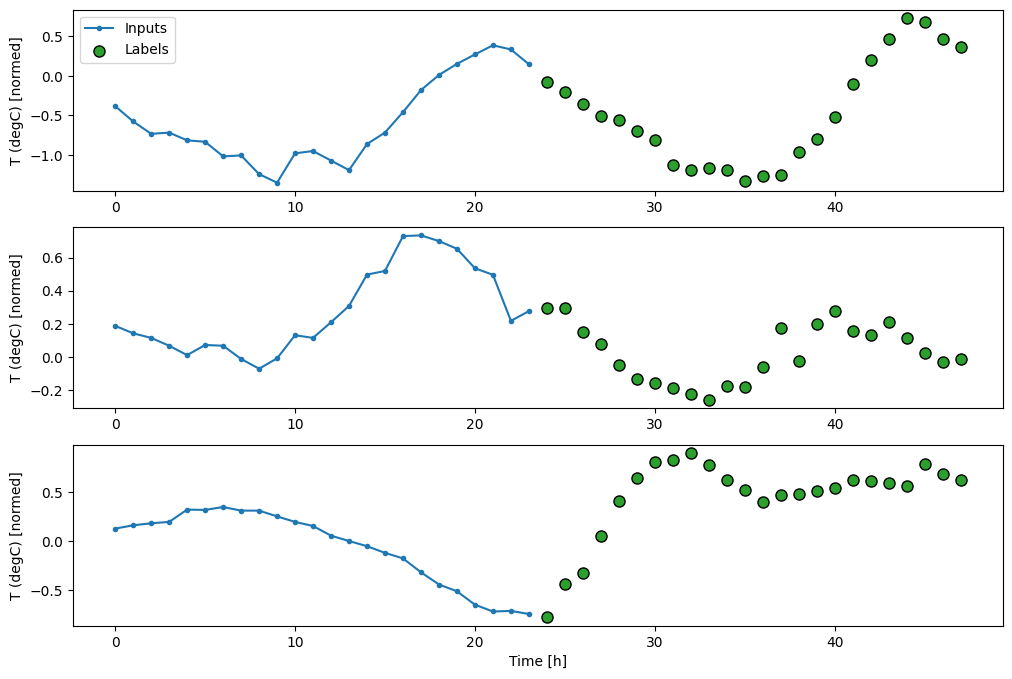
Linhas de base
Uma linha de base simples para esta tarefa é repetir a última etapa de tempo de entrada para o número necessário de etapas de tempo de saída:
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007
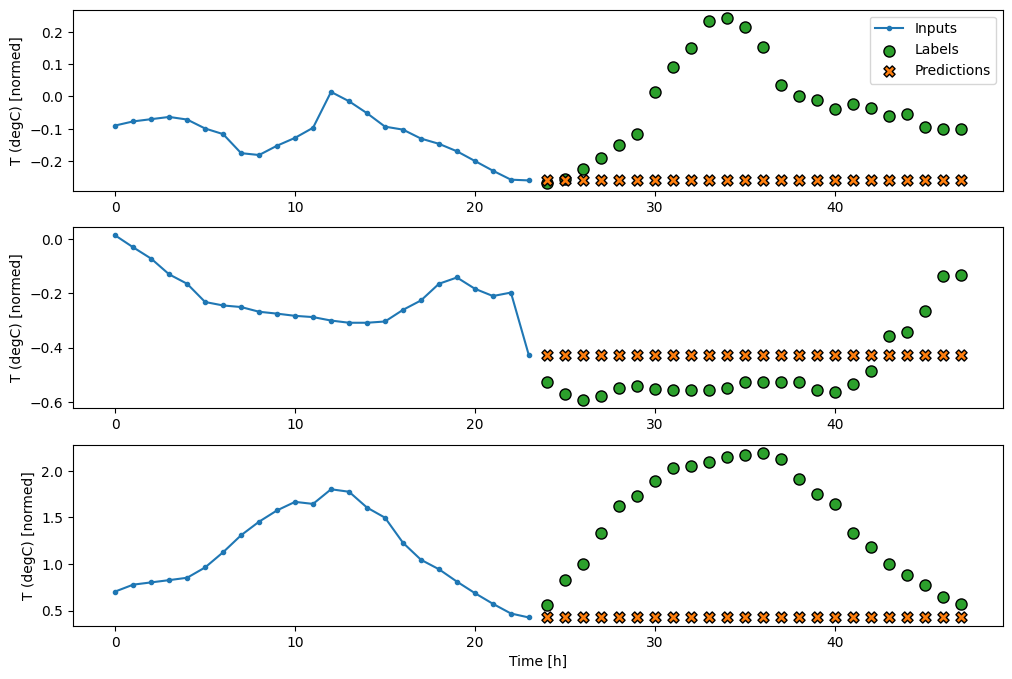
Como essa tarefa é prever 24 horas no futuro, considerando 24 horas no passado, outra abordagem simples é repetir o dia anterior, assumindo que amanhã será semelhante:
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
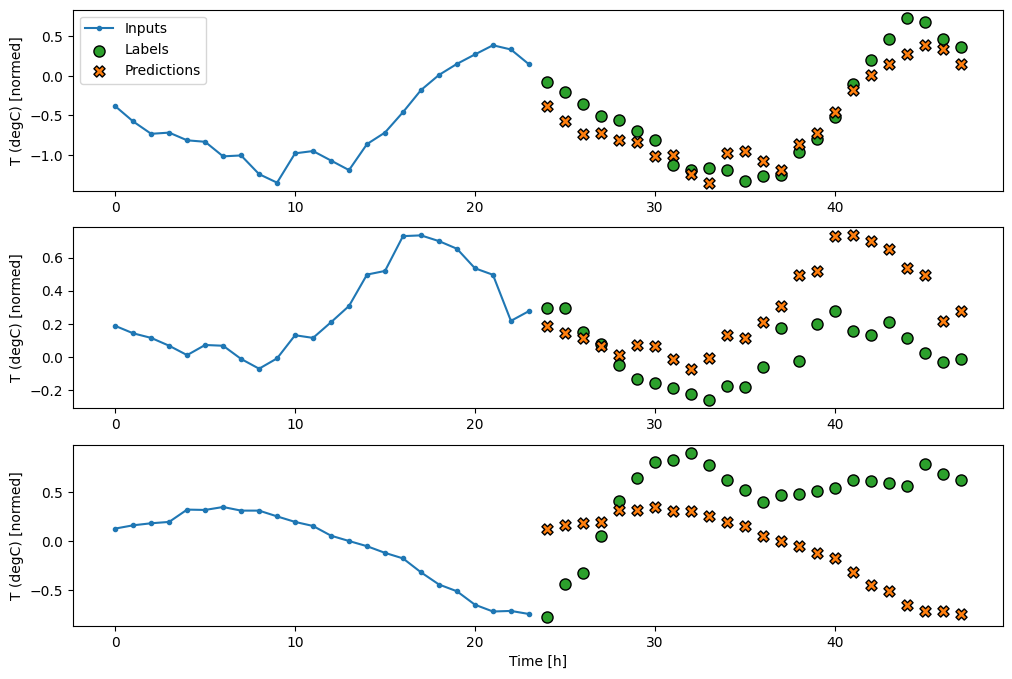
Modelos de disparo único
Uma abordagem de alto nível para esse problema é usar um modelo "single-shot", em que o modelo faz a previsão da sequência inteira em uma única etapa.
Isso pode ser implementado de forma eficiente como um tf.keras.layers.Dense com OUT_STEPS*features unidades de saída. O modelo só precisa remodelar essa saída para o necessário (OUTPUT_STEPS, features) .
Linear
Um modelo linear simples baseado na última etapa de tempo de entrada se sai melhor do que qualquer uma das linhas de base, mas tem pouca potência. O modelo precisa prever etapas de tempo OUTPUT_STEPS , a partir de uma única etapa de tempo de entrada com uma projeção linear. Ele só pode capturar uma fatia de baixa dimensão do comportamento, provavelmente com base principalmente na hora do dia e na época do ano.
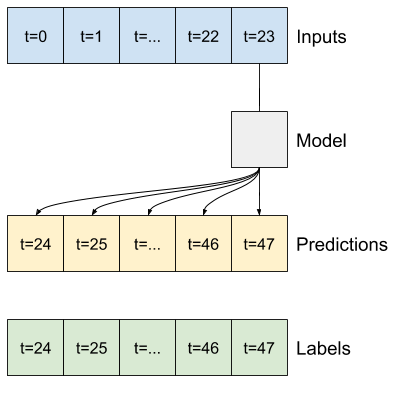
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053
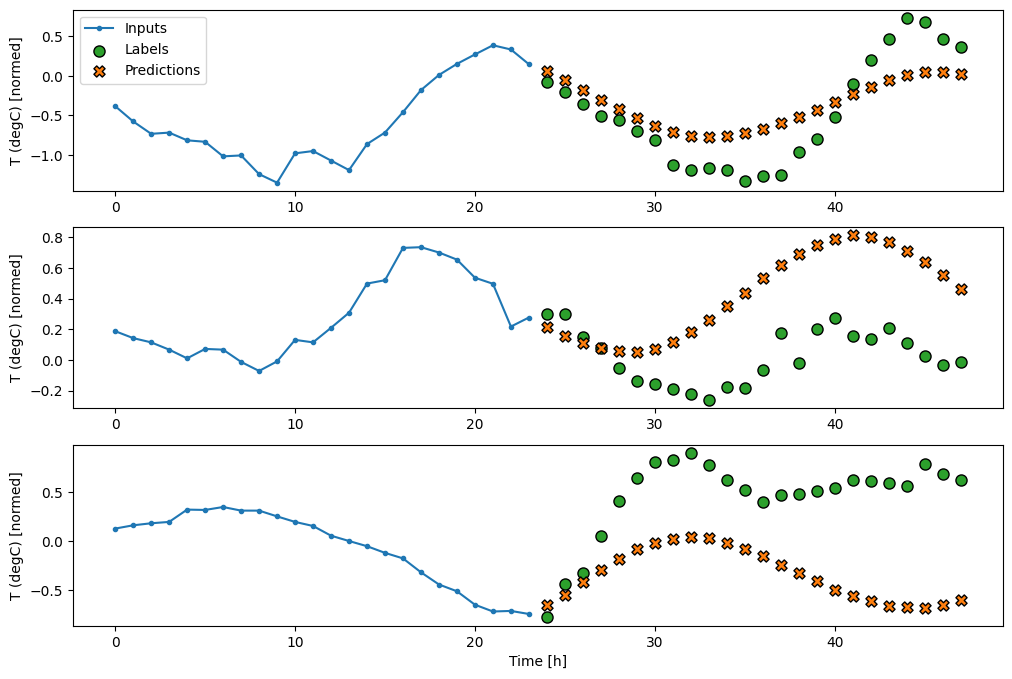
Denso
Adicionar um tf.keras.layers.Dense entre a entrada e a saída dá mais poder ao modelo linear, mas ainda é baseado apenas em um único passo de tempo de entrada.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
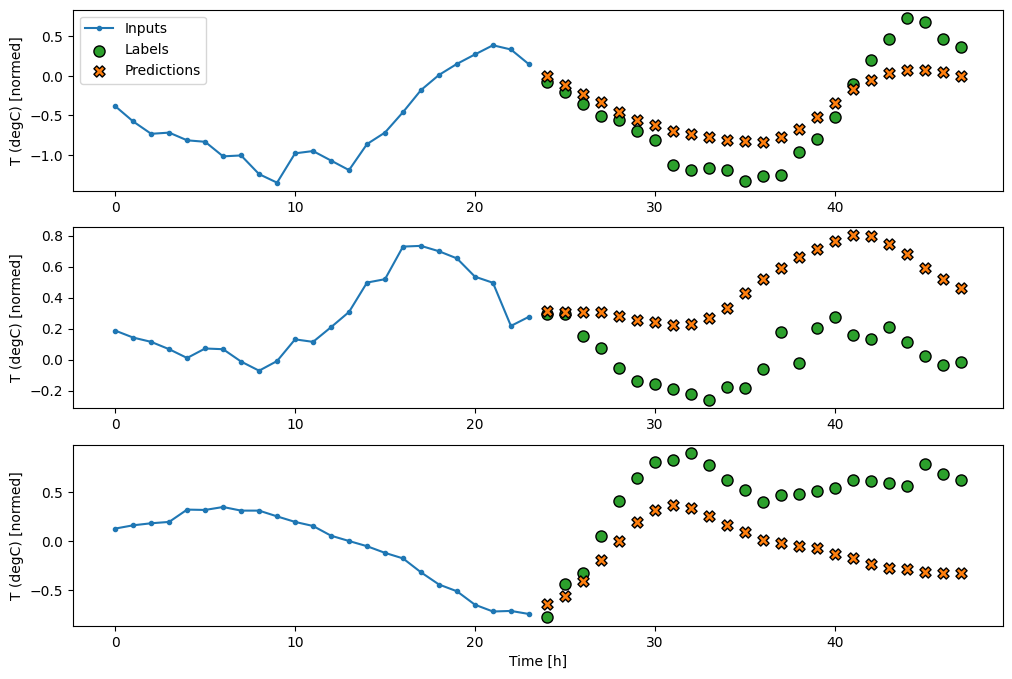
CNN
Um modelo convolucional faz previsões com base em um histórico de largura fixa, o que pode levar a um desempenho melhor do que o modelo denso, pois pode ver como as coisas estão mudando ao longo do tempo:
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
RN
Um modelo recorrente pode aprender a usar um longo histórico de entradas, se for relevante para as previsões que o modelo está fazendo. Aqui o modelo acumulará o estado interno por 24 horas, antes de fazer uma única previsão para as próximas 24 horas.
Neste formato single-shot, o LSTM só precisa produzir uma saída na última etapa de tempo, então defina return_sequences=False em tf.keras.layers.LSTM .
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
Avançado: modelo autorregressivo
Todos os modelos acima preveem toda a sequência de saída em uma única etapa.
Em alguns casos, pode ser útil para o modelo decompor essa previsão em etapas de tempo individuais. Então, a saída de cada modelo pode ser realimentada em cada etapa e as previsões podem ser feitas condicionadas à anterior, como no clássico Gerando Sequências com Redes Neurais Recorrentes .
Uma clara vantagem desse estilo de modelo é que ele pode ser configurado para produzir saída com comprimento variável.
Você pode pegar qualquer um dos modelos de várias saídas de etapa única treinados na primeira metade deste tutorial e executar em um loop de feedback autorregressivo, mas aqui você se concentrará na construção de um modelo que foi explicitamente treinado para fazer isso.
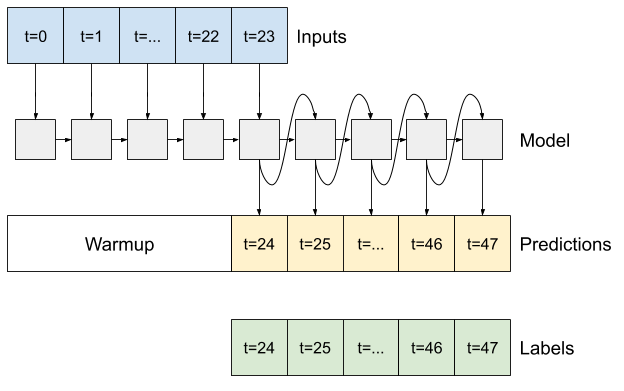
RN
Este tutorial cria apenas um modelo RNN autorregressivo, mas esse padrão pode ser aplicado a qualquer modelo projetado para gerar uma única etapa de tempo.
O modelo terá a mesma forma básica dos modelos LSTM de etapa única anteriores: uma camada tf.keras.layers.LSTM seguida por uma camada tf.keras.layers.Dense que converte as saídas da camada LSTM em previsões de modelo.
Um tf.keras.layers.LSTM é um tf.keras.layers.LSTMCell envolto no tf.keras.layers.RNN de nível superior que gerencia o estado e os resultados da sequência para você (Confira as Redes Neurais Recorrentes (RNN) com Keras guia para detalhes).
Nesse caso, o modelo precisa gerenciar manualmente as entradas para cada etapa, portanto, ele usa tf.keras.layers.LSTMCell diretamente para a interface de etapa de tempo única de nível inferior.
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
O primeiro método que este modelo precisa é um método de warmup para inicializar seu estado interno com base nas entradas. Uma vez treinado, este estado irá capturar as partes relevantes do histórico de entrada. Isso é equivalente ao modelo LSTM de etapa única anterior:
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
Este método retorna uma única previsão de passo de tempo e o estado interno do LSTM :
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
Com o estado do RNN e uma previsão inicial, agora você pode continuar iterando o modelo que alimenta as previsões em cada etapa para trás como entrada.
A abordagem mais simples para coletar as previsões de saída é usar uma lista Python e um tf.stack após o loop.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
Teste este modelo nas entradas de exemplo:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
Agora, treine o modelo:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
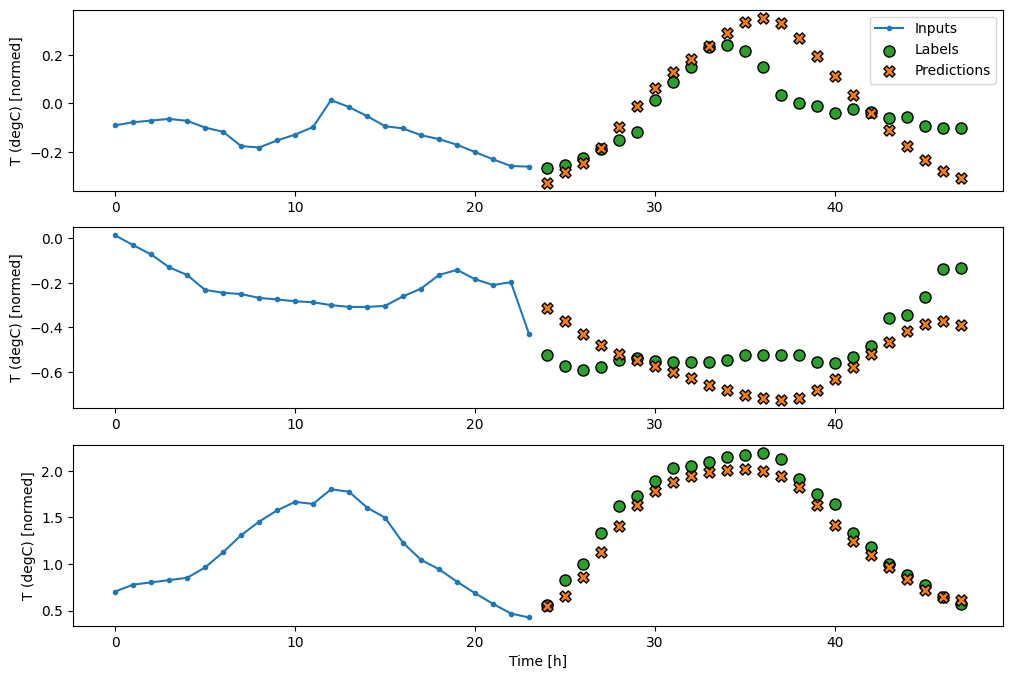
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
Desempenho
Há retornos claramente decrescentes em função da complexidade do modelo neste problema:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()
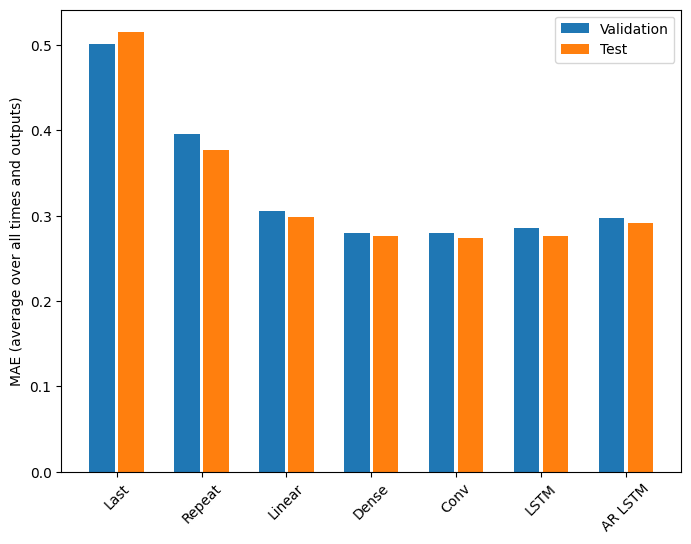
As métricas para os modelos de várias saídas na primeira metade deste tutorial mostram a média de desempenho em todos os recursos de saída. Esses desempenhos são semelhantes, mas também calculados em intervalos de tempo de saída.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
Os ganhos obtidos ao passar de um modelo denso para modelos convolucionais e recorrentes são apenas alguns por cento (se houver), e o modelo autorregressivo teve um desempenho claramente pior. Portanto, essas abordagens mais complexas podem não valer a pena nesse problema, mas não havia como saber sem tentar, e esses modelos podem ser úteis para o seu problema.
Próximos passos
Este tutorial foi uma introdução rápida à previsão de séries temporais usando o TensorFlow.
Para saber mais, consulte:
- Capítulo 15 de Aprendizado de máquina prático com Scikit-Learn, Keras e TensorFlow , 2ª edição.
- Capítulo 6 de Deep Learning com Python .
- Lição 8 da introdução da Udacity ao TensorFlow para aprendizado profundo , incluindo os cadernos de exercícios .
Além disso, lembre-se de que você pode implementar qualquer modelo clássico de série temporal no TensorFlow — este tutorial se concentra apenas na funcionalidade integrada do TensorFlow.
