ดูบน TensorFlow.org ดูบน TensorFlow.org |  ทำงานใน Google Colab ทำงานใน Google Colab |  ดูแหล่งที่มาบน GitHub ดูแหล่งที่มาบน GitHub |  ดาวน์โหลดโน๊ตบุ๊ค ดาวน์โหลดโน๊ตบุ๊ค |
เสียงรบกวนมีอยู่ในคอมพิวเตอร์ควอนตัมสมัยใหม่ Qubits มีความอ่อนไหวต่อการรบกวนจากสภาพแวดล้อมโดยรอบ การประดิษฐ์ที่ไม่สมบูรณ์ TLS และบางครั้งแม้แต่ รังสีแกมมา จนกว่าจะมีการแก้ไขข้อผิดพลาดในวงกว้าง อัลกอริทึมในปัจจุบันจะต้องสามารถทำงานต่อไปได้เมื่อมีสัญญาณรบกวน สิ่งนี้ทำให้อัลกอริธึมการทดสอบภายใต้สัญญาณรบกวนเป็นขั้นตอนสำคัญสำหรับการตรวจสอบความถูกต้องของอัลกอริธึมควอนตัม / โมเดลที่จะทำงานในคอมพิวเตอร์ควอนตัมในปัจจุบัน
ในบทช่วยสอนนี้ คุณจะสำรวจพื้นฐานของการจำลองวงจรที่มีสัญญาณรบกวนใน TFQ ผ่าน tfq.layers API ระดับสูง
ติดตั้ง
pip install tensorflow==2.7.0 tensorflow-quantum
pip install -q git+https://github.com/tensorflow/docs
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
2022-02-04 12:35:30.853880: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. ทำความเข้าใจเสียงควอนตัม
1.1 เสียงวงจรพื้นฐาน
สัญญาณรบกวนบนคอมพิวเตอร์ควอนตัมส่งผลกระทบต่อตัวอย่างบิตสตริงที่คุณสามารถวัดได้ วิธีหนึ่งที่เข้าใจง่ายที่คุณสามารถเริ่มคิดเกี่ยวกับสิ่งนี้คือคอมพิวเตอร์ควอนตัมที่มีเสียงดังจะ "แทรก", "ลบ" หรือ "แทนที่" เกทในตำแหน่งสุ่มเช่นแผนภาพด้านล่าง:
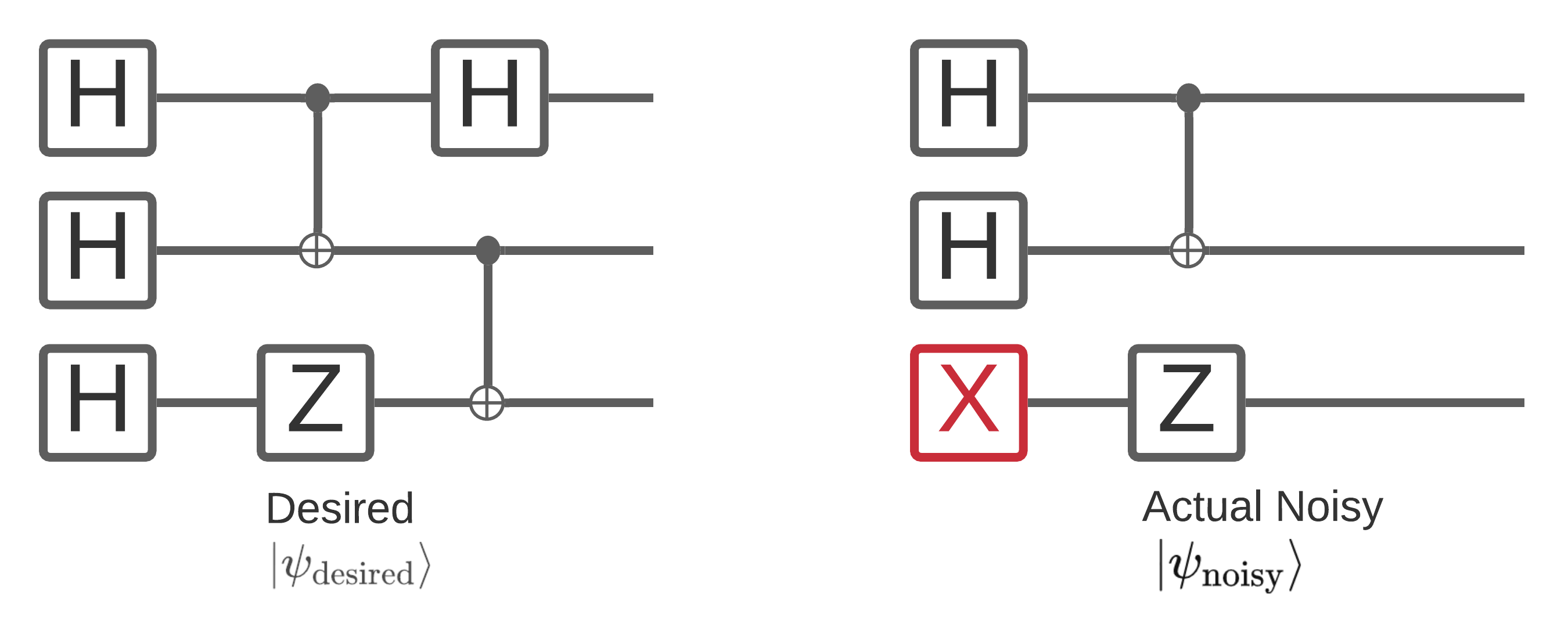
จากสัญชาตญาณนี้ เมื่อคุณต้องรับมือกับเสียงรบกวน คุณจะไม่ได้ใช้สถานะบริสุทธิ์เพียงสถานะเดียวอีกต่อไป \(|\psi \rangle\) แต่แทนที่จะจัดการกับกลุ่มของสัญญาณรบกวนที่เป็นไปได้ ทั้งหมด ของวงจรที่คุณต้องการ: \(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) โดยที่ \(p_j\) ให้ความน่าจะเป็นที่ระบบอยู่ใน \(|\psi_j \rangle\)
ทบทวนภาพด้านบนอีกครั้ง หากเราทราบล่วงหน้าว่า 90% ของเวลาที่ระบบของเราทำงานได้อย่างสมบูรณ์ หรือผิดพลาด 10% ของเวลาด้วยโหมดความล้มเหลวเพียงโหมดเดียว กลุ่มของเราจะเป็น:
\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)
หากมีมากกว่าหนึ่งวิธีที่วงจรของเราอาจผิดพลาดได้ \(\rho\) ทั้งมวลจะมีคำศัพท์มากกว่าสองคำ (หนึ่งคำสำหรับการทำให้เกิดสัญญาณรบกวนใหม่แต่ละครั้งที่อาจเกิดขึ้น) \(\rho\) เรียกว่า เมทริกซ์ความหนาแน่นที่ อธิบายระบบที่มีเสียงดังของคุณ
1.2 การใช้ช่องสัญญาณเพื่อสร้างแบบจำลองสัญญาณรบกวนวงจร
น่าเสียดายในทางปฏิบัติ แทบเป็นไปไม่ได้เลยที่จะรู้ว่าวงจรของคุณอาจผิดพลาดและความน่าจะเป็นที่แน่นอนได้อย่างไร สมมติฐานง่ายๆ ที่คุณสามารถทำได้คือหลังจากการทำงานแต่ละครั้งในวงจรของคุณ จะมี ช่องสัญญาณ บางประเภทที่จับภาพคร่าวๆ ว่าการทำงานนั้นอาจมีข้อผิดพลาดอย่างไร คุณสามารถสร้างวงจรด้วยสัญญาณรบกวนได้อย่างรวดเร็ว:
def x_circuit(qubits):
"""Produces an X wall circuit on `qubits`."""
return cirq.Circuit(cirq.X.on_each(*qubits))
def make_noisy(circuit, p):
"""Add a depolarization channel to all qubits in `circuit` before measurement."""
return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))
my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit
my_noisy_circuit
คุณสามารถตรวจสอบเมทริกซ์ความหนาแน่นที่ไม่มีเสียง \(\rho\) ด้วย:
rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)
array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)
และเมทริกซ์ความหนาแน่นที่มีเสียงดัง \(\rho\) ด้วย:
rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)
array([[0.111+0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.222+0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0.222+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0.444+0.j]], dtype=complex64)
ตัวยึดตำแหน่ง32เมื่อเปรียบเทียบ \( \rho \) ที่แตกต่างกันทั้งสอง คุณจะเห็นว่าสัญญาณรบกวนส่งผลกระทบต่อแอมพลิจูดของรัฐ (และความน่าจะเป็นในการสุ่มตัวอย่าง) ในกรณีที่ไม่มีเสียง คุณมักจะคาดหวังให้สุ่มตัวอย่างสถานะ \( |11\rangle \) แต่ในสภาวะที่มีเสียงดัง ตอนนี้มีความเป็นไปได้ที่ไม่เป็นศูนย์ในการสุ่มตัวอย่าง \( |00\rangle \) หรือ \( |01\rangle \) หรือ \( |10\rangle \) เช่นกัน:
"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
plot_samples(my_noisy_circuit)
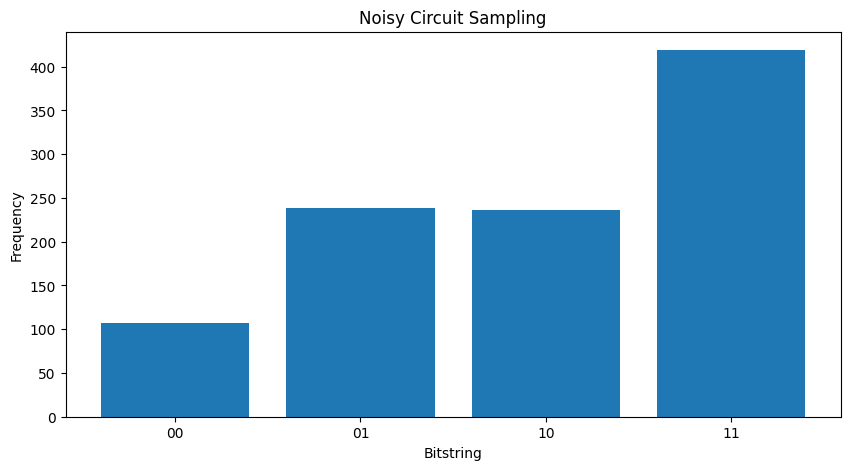
หากไม่มีเสียงรบกวนใด ๆ คุณจะได้รับ \(|11\rangle\)เสมอ :
"""Sample from my_circuit."""
plot_samples(my_circuit)
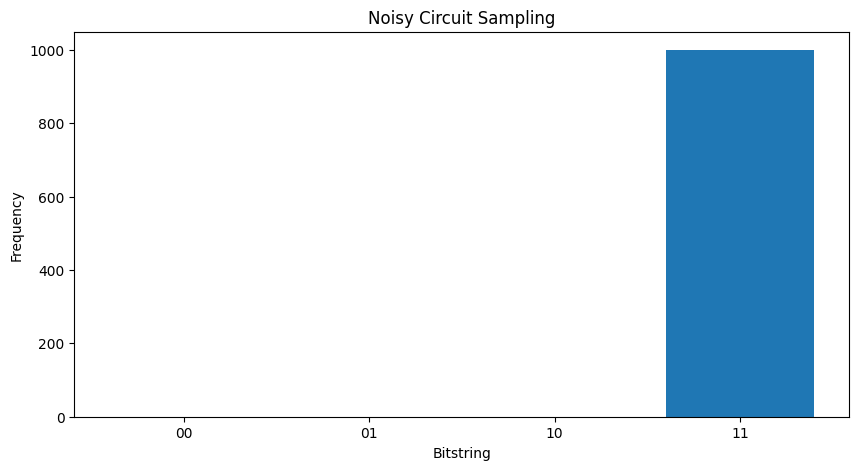
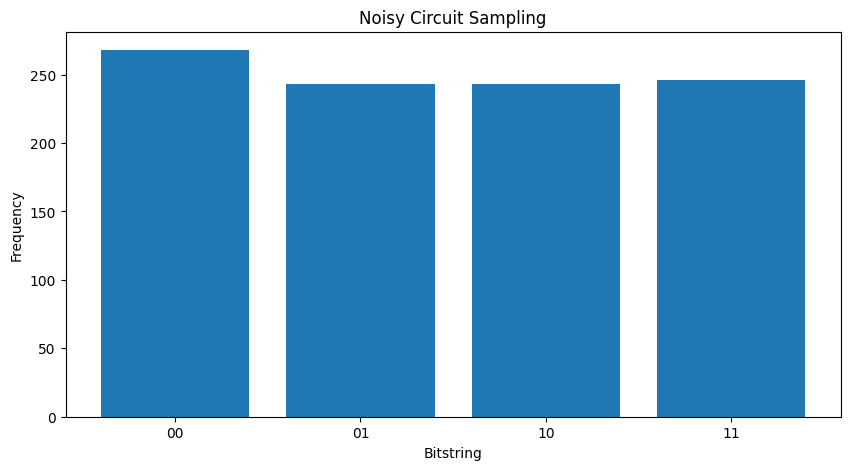
หากคุณเพิ่มเสียงรบกวนอีกเล็กน้อย จะยากขึ้นเรื่อยๆ ในการแยกแยะพฤติกรรมที่ต้องการ (การสุ่มตัวอย่าง \(|11\rangle\) ) จากเสียงรบกวน:
my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)
2. เสียงพื้นฐานใน TFQ
ด้วยความเข้าใจว่าเสียงสามารถส่งผลกระทบต่อการทำงานของวงจรได้อย่างไร คุณสามารถสำรวจว่าเสียงรบกวนทำงานอย่างไรใน TFQ TensorFlow Quantum ใช้การจำลองแบบมอนติคาร์โล/วิถีโคจรเป็นทางเลือกแทนการจำลองเมทริกซ์ความหนาแน่น เนื่องจากความซับซ้อนของหน่วยความจำของการจำลองเมทริกซ์ความหนาแน่นจำกัดการจำลองขนาดใหญ่ที่ <= 20 qubits ด้วยวิธีการจำลองเมทริกซ์ความหนาแน่นเต็มรูปแบบแบบดั้งเดิม Monte-carlo / trajectory แลกเปลี่ยนค่าใช้จ่ายนี้ในหน่วยความจำสำหรับค่าใช้จ่ายเพิ่มเติมในเวลา ตัวเลือก backend='noisy' ใช้ได้กับ tfq.layers.Sample , tfq.layers.SampledExpectation และ tfq.layers.Expectation (ในกรณีของ Expectation สิ่งนี้จะเพิ่มพารามิเตอร์การ repetitions ที่จำเป็น)
2.1 การสุ่มตัวอย่างที่มีเสียงดังใน TFQ
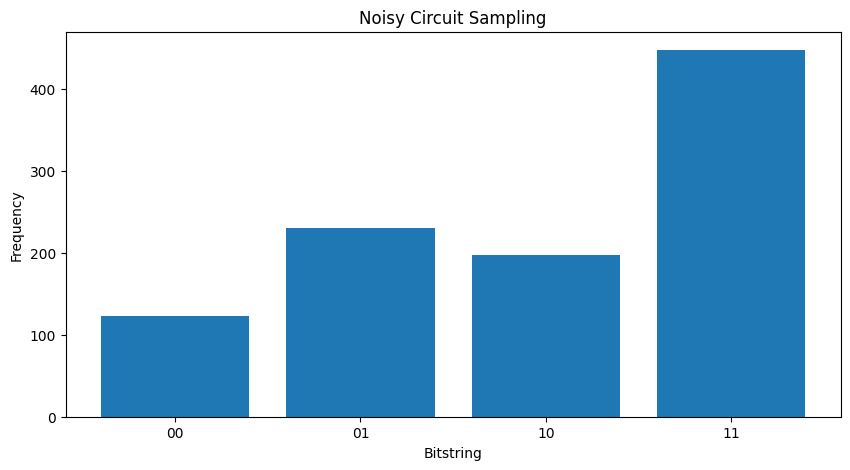
ในการสร้างพล็อตด้านบนใหม่โดยใช้ TFQ และการจำลองวิถี คุณสามารถใช้ tfq.layers.Sample
"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)
numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
<BarContainer object of 4 artists>
2.2 ความคาดหวังตามตัวอย่างที่มีเสียงดัง
ในการคำนวณความคาดหวังตามตัวอย่างที่มีเสียงดัง คุณสามารถใช้ tfq.layers.SampleExpectation :
some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables
[cirq.X(cirq.GridQubit(0, 0)),
cirq.Z(cirq.GridQubit(0, 0)),
cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]
คำนวณการประมาณการความคาดหวังที่ไม่มีเสียงผ่านการสุ่มตัวอย่างจากวงจร:
noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()
array([[-0.0028, -1. , 1.0264]], dtype=float32)ตัวยึดตำแหน่ง42
เปรียบเทียบกับรุ่นที่มีเสียงดัง:
noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()
array([[ 0.0242 , -0.33200002, 1.0138001 ],
[ 0.0108 , -0.0012 , 0.9502 ]], dtype=float32)
คุณจะเห็นว่าสัญญาณรบกวนส่งผลกระทบกับความแม่นยำของ \(\langle \psi | Z | \psi \rangle\) โดยเฉพาะ โดย my_really_noisy_circuit จะพุ่งไปที่ 0 อย่างรวดเร็ว
2.3 การคำนวณความคาดหวังในการวิเคราะห์ที่มีเสียงดัง
การคำนวณความคาดหวังในการวิเคราะห์ที่มีเสียงดังนั้นเกือบจะเหมือนกับด้านบน:
noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()
array([[ 1.9106853e-15, -1.0000000e+00, 1.0000002e+00]], dtype=float32)
noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()
array([[ 1.9106850e-15, -3.3359998e-01, 1.0000000e+00],
[ 1.9106857e-15, -3.8000005e-03, 1.0000001e+00]], dtype=float32)
3. โมเดลไฮบริดและสัญญาณรบกวนข้อมูลควอนตัม
ตอนนี้ คุณได้ใช้การจำลองวงจรที่มีสัญญาณรบกวนใน TFQ แล้ว คุณสามารถทดลองว่าเสียงส่งผลกระทบต่อแบบจำลองควอนตัมคลาสสิกและควอนตัมแบบไฮบริดอย่างไร โดยการเปรียบเทียบและเปรียบเทียบประสิทธิภาพเสียงกับเสียงที่ไม่มีเสียงรบกวน การตรวจสอบครั้งแรกที่ดีเพื่อดูว่าโมเดลหรืออัลกอริธึมทนทานต่อสัญญาณรบกวนหรือไม่ คือการทดสอบภายใต้โมเดลการสลับขั้วแบบกว้างของวงจรซึ่งมีลักษณะดังนี้:
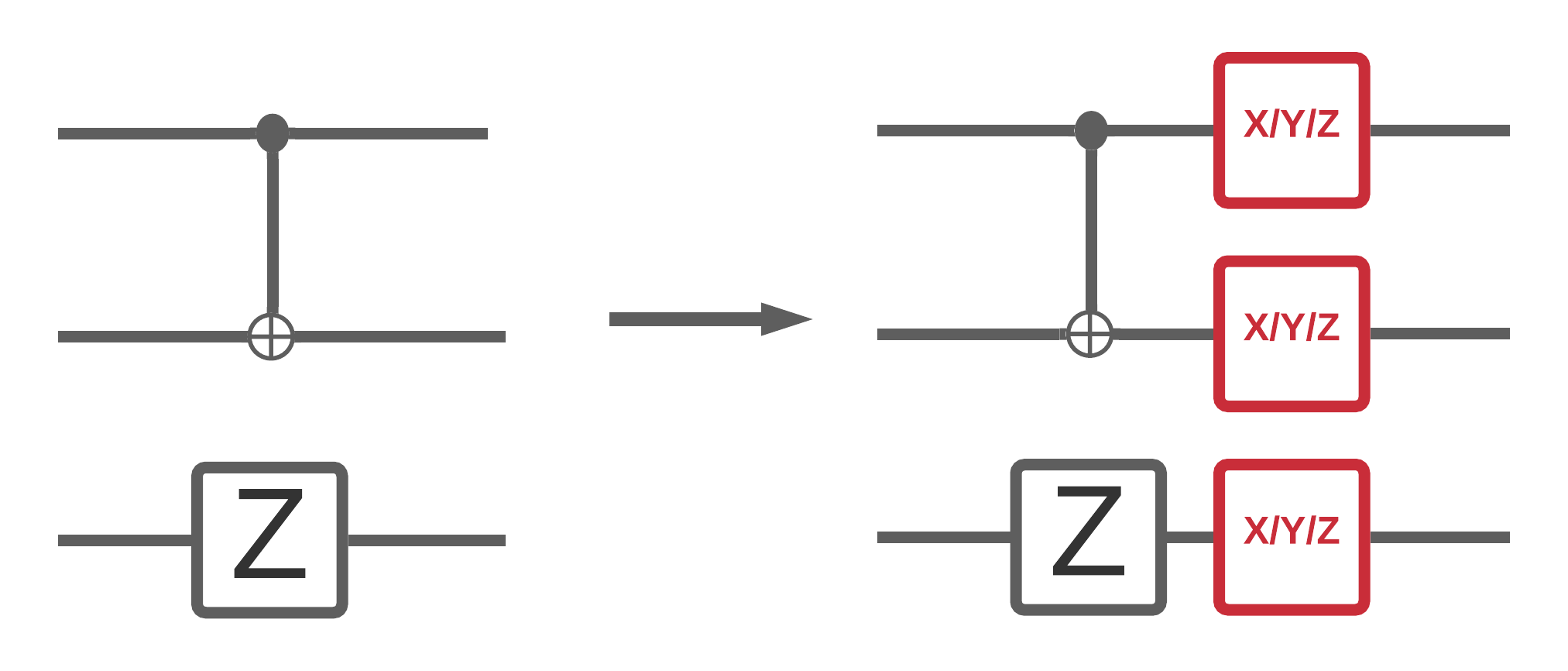
โดยที่การแบ่งเวลาของวงจรแต่ละครั้ง (บางครั้งเรียกว่าโมเมนต์) มีช่องสัญญาณขั้วบวกต่อท้ายหลังจากการทำงานของเกตแต่ละส่วนในช่วงเวลานั้น ช่อง depolarizing พร้อมใช้หนึ่งใน \(\{X, Y, Z \}\) ที่มีความน่าจะ \(p\) หรือไม่ใช้อะไร (เก็บการดำเนินการดั้งเดิม) ด้วยความน่าจะ \(1-p\)
3.1 ข้อมูล
สำหรับตัวอย่างนี้ คุณสามารถใช้วงจรที่เตรียมไว้บางส่วนในโมดูล tfq.datasets เป็นข้อมูลการฝึก:
qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 184451072/184449737 [==============================] - 2s 0us/step 184459264/184449737 [==============================] - 2s 0us/step
การเขียนฟังก์ชันตัวช่วยเล็กๆ น้อยๆ จะช่วยในการสร้างข้อมูลสำหรับกรณีที่มีเสียงดังหรือไม่มีเสียง:
def get_data(qubits, depolarize_p=0.):
"""Return quantum data circuits and labels in `tf.Tensor` form."""
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
if depolarize_p >= 1e-5:
circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
tmp = list(zip(circuits, labels))
random.shuffle(tmp)
circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])
return circuits_tensor, labels_tensor
3.2 กำหนดรูปแบบวงจร
เมื่อคุณมีข้อมูลควอนตัมในรูปแบบของวงจรแล้ว คุณจะต้องมีวงจรเพื่อสร้างแบบจำลองข้อมูลนี้ เช่นเดียวกับข้อมูลที่คุณสามารถเขียนฟังก์ชันตัวช่วยเพื่อสร้างวงจรนี้โดยอาจมีสัญญาณรบกวน
def modelling_circuit(qubits, depth, depolarize_p=0.):
"""A simple classifier circuit."""
dim = len(qubits)
ret = cirq.Circuit(cirq.H.on_each(*qubits))
for i in range(depth):
# Entangle layer.
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
# Learnable rotation layer.
# i_params = sympy.symbols(f'layer-{i}-0:{dim}')
param = sympy.Symbol(f'layer-{i}')
single_qb = cirq.X
if i % 2 == 1:
single_qb = cirq.Y
ret += cirq.Circuit(single_qb(q) ** param for q in qubits)
if depolarize_p >= 1e-5:
ret = ret.with_noise(cirq.depolarize(depolarize_p))
return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]
modelling_circuit(qubits, 3)[0]
3.3 การสร้างแบบจำลองและการฝึกอบรม
ด้วยข้อมูลและวงจรโมเดลที่สร้างขึ้น ฟังก์ชันตัวช่วยขั้นสุดท้ายที่คุณต้องการคือฟังก์ชันที่สามารถประกอบทั้งควอนตัมไฮบริด tf.keras.Model ที่ส่งเสียงดังหรือไม่มีเสียงได้ รุ่น :
def build_keras_model(qubits, depolarize_p=0.):
"""Prepare a noisy hybrid quantum classical Keras model."""
spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
if depolarize_p >= 1e-5:
quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
else:
quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)
intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
post_process = tf.keras.layers.Dense(1)(intermediate)
return tf.keras.Model(inputs=[spin_input], outputs=[post_process])
4. เปรียบเทียบประสิทธิภาพ
4.1 พื้นฐานที่ไม่มีเสียง
ด้วยการสร้างข้อมูลและรหัสการสร้างแบบจำลองของคุณ ขณะนี้คุณสามารถเปรียบเทียบและเปรียบเทียบประสิทธิภาพของแบบจำลองในการตั้งค่าที่ไร้เสียงรบกวนและเสียงรบกวน ขั้นแรก คุณสามารถเรียกใช้การฝึกอบรมแบบไร้เสียงอ้างอิงได้:
training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)
phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)
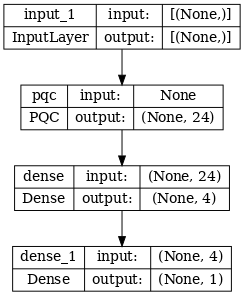
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
y=noiseless_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 1s 133ms/step - loss: 0.7212 - accuracy: 0.4688 - val_loss: 0.6834 - val_accuracy: 0.5000 Epoch 2/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6787 - accuracy: 0.4688 - val_loss: 0.6640 - val_accuracy: 0.5000 Epoch 3/50 4/4 [==============================] - 0s 76ms/step - loss: 0.6637 - accuracy: 0.4688 - val_loss: 0.6529 - val_accuracy: 0.5000 Epoch 4/50 4/4 [==============================] - 0s 78ms/step - loss: 0.6505 - accuracy: 0.4688 - val_loss: 0.6423 - val_accuracy: 0.5000 Epoch 5/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6409 - accuracy: 0.4688 - val_loss: 0.6322 - val_accuracy: 0.5000 Epoch 6/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6300 - accuracy: 0.4844 - val_loss: 0.6187 - val_accuracy: 0.5000 Epoch 7/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6171 - accuracy: 0.5781 - val_loss: 0.6007 - val_accuracy: 0.5000 Epoch 8/50 4/4 [==============================] - 0s 79ms/step - loss: 0.6008 - accuracy: 0.6250 - val_loss: 0.5825 - val_accuracy: 0.5833 Epoch 9/50 4/4 [==============================] - 0s 76ms/step - loss: 0.5864 - accuracy: 0.6406 - val_loss: 0.5610 - val_accuracy: 0.6667 Epoch 10/50 4/4 [==============================] - 0s 77ms/step - loss: 0.5670 - accuracy: 0.6719 - val_loss: 0.5406 - val_accuracy: 0.8333 Epoch 11/50 4/4 [==============================] - 0s 79ms/step - loss: 0.5474 - accuracy: 0.6875 - val_loss: 0.5173 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 0s 77ms/step - loss: 0.5276 - accuracy: 0.7188 - val_loss: 0.4941 - val_accuracy: 0.9167 Epoch 13/50 4/4 [==============================] - 0s 75ms/step - loss: 0.5066 - accuracy: 0.7500 - val_loss: 0.4686 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4838 - accuracy: 0.7812 - val_loss: 0.4437 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4618 - accuracy: 0.8281 - val_loss: 0.4182 - val_accuracy: 0.9167 Epoch 16/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4386 - accuracy: 0.8281 - val_loss: 0.3930 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 0s 79ms/step - loss: 0.4158 - accuracy: 0.8438 - val_loss: 0.3673 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 0s 79ms/step - loss: 0.3944 - accuracy: 0.8438 - val_loss: 0.3429 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 0s 77ms/step - loss: 0.3735 - accuracy: 0.8594 - val_loss: 0.3203 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 0s 77ms/step - loss: 0.3535 - accuracy: 0.8750 - val_loss: 0.2998 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 0s 78ms/step - loss: 0.3345 - accuracy: 0.8906 - val_loss: 0.2815 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 0s 76ms/step - loss: 0.3168 - accuracy: 0.8906 - val_loss: 0.2640 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 0s 76ms/step - loss: 0.3017 - accuracy: 0.9062 - val_loss: 0.2465 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2840 - accuracy: 0.9219 - val_loss: 0.2328 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2700 - accuracy: 0.9219 - val_loss: 0.2181 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2566 - accuracy: 0.9219 - val_loss: 0.2053 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 0s 77ms/step - loss: 0.2445 - accuracy: 0.9375 - val_loss: 0.1935 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2332 - accuracy: 0.9375 - val_loss: 0.1839 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 0s 78ms/step - loss: 0.2227 - accuracy: 0.9375 - val_loss: 0.1734 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2145 - accuracy: 0.9375 - val_loss: 0.1630 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2047 - accuracy: 0.9375 - val_loss: 0.1564 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1971 - accuracy: 0.9375 - val_loss: 0.1525 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1894 - accuracy: 0.9531 - val_loss: 0.1464 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 0s 74ms/step - loss: 0.1825 - accuracy: 0.9531 - val_loss: 0.1407 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1771 - accuracy: 0.9531 - val_loss: 0.1330 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1704 - accuracy: 0.9531 - val_loss: 0.1288 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1647 - accuracy: 0.9531 - val_loss: 0.1237 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 0s 80ms/step - loss: 0.1603 - accuracy: 0.9531 - val_loss: 0.1221 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1551 - accuracy: 0.9688 - val_loss: 0.1177 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1509 - accuracy: 0.9688 - val_loss: 0.1136 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1466 - accuracy: 0.9688 - val_loss: 0.1110 - val_accuracy: 1.0000 Epoch 42/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1426 - accuracy: 0.9688 - val_loss: 0.1083 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1386 - accuracy: 0.9688 - val_loss: 0.1050 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 0s 83ms/step - loss: 0.1362 - accuracy: 0.9688 - val_loss: 0.0989 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 0s 78ms/step - loss: 0.1324 - accuracy: 0.9688 - val_loss: 0.0978 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1290 - accuracy: 0.9688 - val_loss: 0.0964 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1265 - accuracy: 0.9688 - val_loss: 0.0929 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1234 - accuracy: 0.9688 - val_loss: 0.0923 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1213 - accuracy: 0.9688 - val_loss: 0.0903 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1182 - accuracy: 0.9688 - val_loss: 0.0885 - val_accuracy: 1.0000
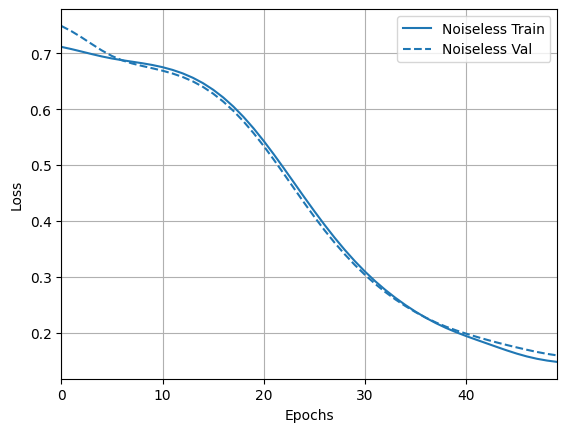
และสำรวจผลลัพธ์และความแม่นยำ:
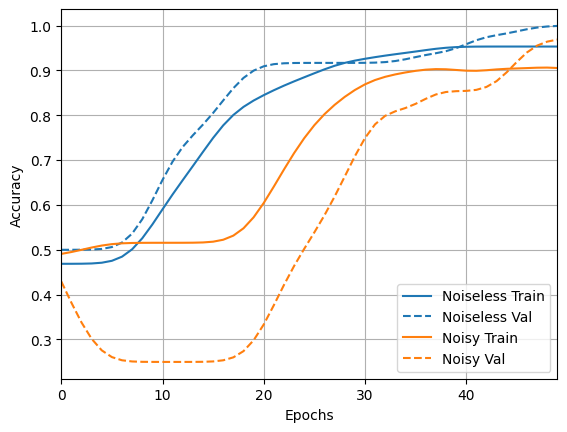
loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)
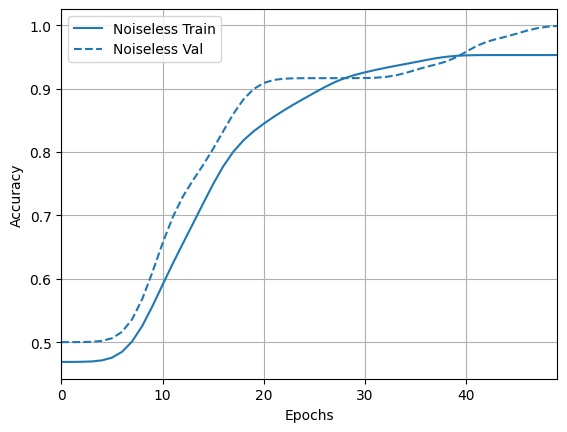
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
acc_plotter.plot(training_histories)
4.2 การเปรียบเทียบที่มีเสียงดัง
ตอนนี้คุณสามารถสร้างโมเดลใหม่ที่มีโครงสร้างรบกวน และเมื่อเปรียบเทียบกับโค้ดด้านบนแล้ว โค้ดก็เกือบจะเหมือนกันทุกประการ:
depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)
noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
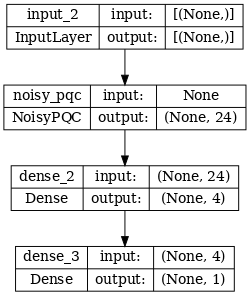
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)
noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
y=noisy_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 8s 2s/step - loss: 0.8265 - accuracy: 0.4844 - val_loss: 0.8369 - val_accuracy: 0.4167 Epoch 2/50 4/4 [==============================] - 7s 2s/step - loss: 0.7613 - accuracy: 0.4844 - val_loss: 0.7695 - val_accuracy: 0.4167 Epoch 3/50 4/4 [==============================] - 7s 2s/step - loss: 0.7151 - accuracy: 0.4844 - val_loss: 0.7290 - val_accuracy: 0.4167 Epoch 4/50 4/4 [==============================] - 7s 2s/step - loss: 0.6915 - accuracy: 0.4844 - val_loss: 0.7014 - val_accuracy: 0.4167 Epoch 5/50 4/4 [==============================] - 7s 2s/step - loss: 0.6837 - accuracy: 0.4844 - val_loss: 0.6811 - val_accuracy: 0.4167 Epoch 6/50 4/4 [==============================] - 7s 2s/step - loss: 0.6717 - accuracy: 0.4844 - val_loss: 0.6801 - val_accuracy: 0.4167 Epoch 7/50 4/4 [==============================] - 7s 2s/step - loss: 0.6739 - accuracy: 0.4844 - val_loss: 0.6726 - val_accuracy: 0.4167 Epoch 8/50 4/4 [==============================] - 7s 2s/step - loss: 0.6713 - accuracy: 0.4844 - val_loss: 0.6661 - val_accuracy: 0.4167 Epoch 9/50 4/4 [==============================] - 7s 2s/step - loss: 0.6710 - accuracy: 0.4844 - val_loss: 0.6667 - val_accuracy: 0.4167 Epoch 10/50 4/4 [==============================] - 7s 2s/step - loss: 0.6669 - accuracy: 0.4844 - val_loss: 0.6627 - val_accuracy: 0.4167 Epoch 11/50 4/4 [==============================] - 7s 2s/step - loss: 0.6637 - accuracy: 0.4844 - val_loss: 0.6550 - val_accuracy: 0.4167 Epoch 12/50 4/4 [==============================] - 7s 2s/step - loss: 0.6616 - accuracy: 0.4844 - val_loss: 0.6593 - val_accuracy: 0.4167 Epoch 13/50 4/4 [==============================] - 7s 2s/step - loss: 0.6536 - accuracy: 0.4844 - val_loss: 0.6514 - val_accuracy: 0.4167 Epoch 14/50 4/4 [==============================] - 7s 2s/step - loss: 0.6489 - accuracy: 0.4844 - val_loss: 0.6481 - val_accuracy: 0.4167 Epoch 15/50 4/4 [==============================] - 7s 2s/step - loss: 0.6491 - accuracy: 0.4844 - val_loss: 0.6484 - val_accuracy: 0.4167 Epoch 16/50 4/4 [==============================] - 7s 2s/step - loss: 0.6389 - accuracy: 0.4844 - val_loss: 0.6396 - val_accuracy: 0.4167 Epoch 17/50 4/4 [==============================] - 7s 2s/step - loss: 0.6307 - accuracy: 0.4844 - val_loss: 0.6337 - val_accuracy: 0.4167 Epoch 18/50 4/4 [==============================] - 7s 2s/step - loss: 0.6296 - accuracy: 0.4844 - val_loss: 0.6260 - val_accuracy: 0.4167 Epoch 19/50 4/4 [==============================] - 7s 2s/step - loss: 0.6194 - accuracy: 0.4844 - val_loss: 0.6282 - val_accuracy: 0.4167 Epoch 20/50 4/4 [==============================] - 7s 2s/step - loss: 0.6095 - accuracy: 0.4844 - val_loss: 0.6138 - val_accuracy: 0.4167 Epoch 21/50 4/4 [==============================] - 7s 2s/step - loss: 0.6075 - accuracy: 0.4844 - val_loss: 0.5874 - val_accuracy: 0.4167 Epoch 22/50 4/4 [==============================] - 7s 2s/step - loss: 0.5981 - accuracy: 0.4844 - val_loss: 0.5981 - val_accuracy: 0.4167 Epoch 23/50 4/4 [==============================] - 7s 2s/step - loss: 0.5823 - accuracy: 0.4844 - val_loss: 0.5818 - val_accuracy: 0.4167 Epoch 24/50 4/4 [==============================] - 7s 2s/step - loss: 0.5768 - accuracy: 0.4844 - val_loss: 0.5617 - val_accuracy: 0.4167 Epoch 25/50 4/4 [==============================] - 7s 2s/step - loss: 0.5651 - accuracy: 0.4844 - val_loss: 0.5638 - val_accuracy: 0.4167 Epoch 26/50 4/4 [==============================] - 7s 2s/step - loss: 0.5496 - accuracy: 0.4844 - val_loss: 0.5532 - val_accuracy: 0.4167 Epoch 27/50 4/4 [==============================] - 7s 2s/step - loss: 0.5340 - accuracy: 0.5000 - val_loss: 0.5345 - val_accuracy: 0.4167 Epoch 28/50 4/4 [==============================] - 7s 2s/step - loss: 0.5297 - accuracy: 0.5156 - val_loss: 0.5308 - val_accuracy: 0.4167 Epoch 29/50 4/4 [==============================] - 7s 2s/step - loss: 0.5120 - accuracy: 0.5312 - val_loss: 0.5224 - val_accuracy: 0.5000 Epoch 30/50 4/4 [==============================] - 7s 2s/step - loss: 0.4992 - accuracy: 0.5781 - val_loss: 0.4921 - val_accuracy: 0.5833 Epoch 31/50 4/4 [==============================] - 7s 2s/step - loss: 0.4823 - accuracy: 0.5938 - val_loss: 0.4975 - val_accuracy: 0.5000 Epoch 32/50 4/4 [==============================] - 7s 2s/step - loss: 0.5025 - accuracy: 0.5781 - val_loss: 0.4814 - val_accuracy: 0.5000 Epoch 33/50 4/4 [==============================] - 7s 2s/step - loss: 0.4655 - accuracy: 0.6562 - val_loss: 0.4391 - val_accuracy: 0.6667 Epoch 34/50 4/4 [==============================] - 7s 2s/step - loss: 0.4552 - accuracy: 0.7031 - val_loss: 0.4528 - val_accuracy: 0.5833 Epoch 35/50 4/4 [==============================] - 7s 2s/step - loss: 0.4516 - accuracy: 0.6719 - val_loss: 0.3993 - val_accuracy: 0.8333 Epoch 36/50 4/4 [==============================] - 7s 2s/step - loss: 0.4320 - accuracy: 0.7656 - val_loss: 0.4225 - val_accuracy: 0.6667 Epoch 37/50 4/4 [==============================] - 7s 2s/step - loss: 0.4060 - accuracy: 0.7656 - val_loss: 0.4001 - val_accuracy: 0.9167 Epoch 38/50 4/4 [==============================] - 7s 2s/step - loss: 0.3858 - accuracy: 0.7812 - val_loss: 0.4152 - val_accuracy: 0.8333 Epoch 39/50 4/4 [==============================] - 7s 2s/step - loss: 0.3964 - accuracy: 0.7656 - val_loss: 0.3899 - val_accuracy: 0.7500 Epoch 40/50 4/4 [==============================] - 7s 2s/step - loss: 0.3640 - accuracy: 0.8125 - val_loss: 0.3689 - val_accuracy: 0.7500 Epoch 41/50 4/4 [==============================] - 7s 2s/step - loss: 0.3676 - accuracy: 0.7812 - val_loss: 0.3786 - val_accuracy: 0.7500 Epoch 42/50 4/4 [==============================] - 7s 2s/step - loss: 0.3466 - accuracy: 0.8281 - val_loss: 0.3313 - val_accuracy: 0.8333 Epoch 43/50 4/4 [==============================] - 7s 2s/step - loss: 0.3520 - accuracy: 0.8594 - val_loss: 0.3398 - val_accuracy: 0.8333 Epoch 44/50 4/4 [==============================] - 7s 2s/step - loss: 0.3402 - accuracy: 0.8438 - val_loss: 0.3135 - val_accuracy: 0.9167 Epoch 45/50 4/4 [==============================] - 7s 2s/step - loss: 0.3253 - accuracy: 0.8281 - val_loss: 0.3469 - val_accuracy: 0.8333 Epoch 46/50 4/4 [==============================] - 7s 2s/step - loss: 0.3239 - accuracy: 0.8281 - val_loss: 0.3038 - val_accuracy: 0.9167 Epoch 47/50 4/4 [==============================] - 7s 2s/step - loss: 0.2948 - accuracy: 0.8594 - val_loss: 0.3056 - val_accuracy: 0.9167 Epoch 48/50 4/4 [==============================] - 7s 2s/step - loss: 0.2972 - accuracy: 0.9219 - val_loss: 0.2699 - val_accuracy: 0.9167 Epoch 49/50 4/4 [==============================] - 7s 2s/step - loss: 0.3041 - accuracy: 0.8281 - val_loss: 0.2754 - val_accuracy: 0.9167 Epoch 50/50 4/4 [==============================] - 7s 2s/step - loss: 0.2944 - accuracy: 0.8750 - val_loss: 0.2988 - val_accuracy: 0.9167
loss_plotter.plot(training_histories)
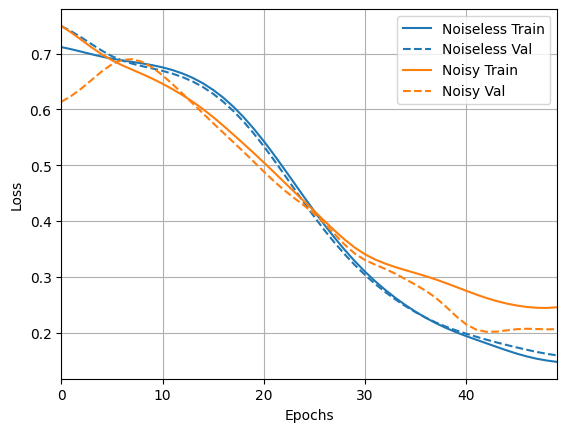
acc_plotter.plot(training_histories)