 مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
ساختمان را از مقایسه های انجام شده در MNIST آموزش، این آموزش به بررسی اثر اخیر هوانگ و همکاران که نشان می دهد چگونه مجموعه داده های مختلف بر مقایسه عملکرد تأثیر می گذارد. در این کار، نویسندگان به دنبال درک این هستند که چگونه و چه زمانی مدلهای یادگیری ماشین کلاسیک میتوانند به خوبی (یا بهتر از) مدلهای کوانتومی یاد بگیرند. این کار همچنین یک جداسازی عملکرد تجربی بین مدل یادگیری ماشین کلاسیک و کوانتومی را از طریق یک مجموعه داده با دقت ساخته شده به نمایش میگذارد. شما:
- یک مجموعه داده با ابعاد کاهش یافته Fashion-MNIST آماده کنید.
- از مدارهای کوانتومی برای برچسب گذاری مجدد مجموعه داده و محاسبه ویژگی های هسته کوانتومی پیش بینی شده (PQK) استفاده کنید.
- یک شبکه عصبی کلاسیک را بر روی مجموعه داده های برچسب گذاری شده مجدد آموزش دهید و عملکرد را با مدلی مقایسه کنید که به ویژگی های PQK دسترسی دارد.
برپایی
pip install tensorflow==2.4.1 tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
1. آماده سازی داده ها
شما با آماده کردن مجموعه داده های fashion-MNIST برای اجرا بر روی یک کامپیوتر کوانتومی شروع خواهید کرد.
1.1 دانلود fashion-MNIST
اولین قدم این است که مجموعه داده سنتی fashion-mnist را دریافت کنید. این را می توان با استفاده از انجام tf.keras.datasets ماژول.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train/255.0, x_test/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Number of original training examples: 60000 Number of original test examples: 10000
مجموعه داده را فیلتر کنید تا فقط تیشرتها/تاپها و لباسها را نگه دارید، کلاسهای دیگر را حذف کنید. در همان زمان تبدیل به برچسب، y ، به منطقی: واقعی برای 0 و غلط برای 3.
def filter_03(x, y):
keep = (y == 0) | (y == 3)
x, y = x[keep], y[keep]
y = y == 0
return x,y
x_train, y_train = filter_03(x_train, y_train)
x_test, y_test = filter_03(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12000 Number of filtered test examples: 2000
print(y_train[0])
plt.imshow(x_train[0, :, :])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7f6db42c3460>

1.2 مقیاس تصاویر را کاهش دهید
درست مانند مثال MNIST، برای اینکه در محدوده کامپیوترهای کوانتومی فعلی قرار بگیرید، باید مقیاس این تصاویر را کاهش دهید. این بار با این حال شما یک تحول PCA به منظور کاهش ابعاد به جای یک استفاده tf.image.resize عملیات.
def truncate_x(x_train, x_test, n_components=10):
"""Perform PCA on image dataset keeping the top `n_components` components."""
n_points_train = tf.gather(tf.shape(x_train), 0)
n_points_test = tf.gather(tf.shape(x_test), 0)
# Flatten to 1D
x_train = tf.reshape(x_train, [n_points_train, -1])
x_test = tf.reshape(x_test, [n_points_test, -1])
# Normalize.
feature_mean = tf.reduce_mean(x_train, axis=0)
x_train_normalized = x_train - feature_mean
x_test_normalized = x_test - feature_mean
# Truncate.
e_values, e_vectors = tf.linalg.eigh(
tf.einsum('ji,jk->ik', x_train_normalized, x_train_normalized))
return tf.einsum('ij,jk->ik', x_train_normalized, e_vectors[:,-n_components:]), \
tf.einsum('ij,jk->ik', x_test_normalized, e_vectors[:, -n_components:])
DATASET_DIM = 10
x_train, x_test = truncate_x(x_train, x_test, n_components=DATASET_DIM)
print(f'New datapoint dimension:', len(x_train[0]))
New datapoint dimension: 10
آخرین مرحله کاهش اندازه مجموعه داده به تنها 1000 نقطه داده آموزشی و 200 نقطه داده آزمایشی است.
N_TRAIN = 1000
N_TEST = 200
x_train, x_test = x_train[:N_TRAIN], x_test[:N_TEST]
y_train, y_test = y_train[:N_TRAIN], y_test[:N_TEST]
print("New number of training examples:", len(x_train))
print("New number of test examples:", len(x_test))
New number of training examples: 1000 New number of test examples: 200
2. برچسب گذاری مجدد و محاسبه ویژگی های PQK
اکنون یک مجموعه داده کوانتومی "stilted" را با ترکیب اجزای کوانتومی و برچسب گذاری مجدد مجموعه داده های کوتاه شده fashion-MNIST که در بالا ایجاد کرده اید، آماده خواهید کرد. برای به دست آوردن بیشترین تفکیک بین روشهای کوانتومی و کلاسیک، ابتدا ویژگیهای PQK را آماده کرده و سپس خروجیها را بر اساس مقادیر آنها برچسبگذاری مجدد میکنید.
2.1 رمزگذاری کوانتومی و ویژگی های PQK
شما یک مجموعه ای جدید از ویژگی های ایجاد، بر اساس x_train ، y_train ، x_test و y_test است که تعریف می شود 1-RDM در تمام کیوبیت از:
\(V(x_{\text{train} } / n_{\text{trotter} }) ^ {n_{\text{trotter} } } U_{\text{1qb} } | 0 \rangle\)
که در آن \(U_\text{1qb}\) یک دیوار از چرخش کیوبیت و \(V(\hat{\theta}) = e^{-i\sum_i \hat{\theta_i} (X_i X_{i+1} + Y_i Y_{i+1} + Z_i Z_{i+1})}\)
ابتدا، می توانید دیوار چرخش های تک کیوبیت را ایجاد کنید:
def single_qubit_wall(qubits, rotations):
"""Prepare a single qubit X,Y,Z rotation wall on `qubits`."""
wall_circuit = cirq.Circuit()
for i, qubit in enumerate(qubits):
for j, gate in enumerate([cirq.X, cirq.Y, cirq.Z]):
wall_circuit.append(gate(qubit) ** rotations[i][j])
return wall_circuit
با نگاه کردن به مدار، میتوانید به سرعت تأیید کنید که این کار میکند:
SVGCircuit(single_qubit_wall(
cirq.GridQubit.rect(1,4), np.random.uniform(size=(4, 3))))
بعد شما می توانید آماده \(V(\hat{\theta})\) با کمک tfq.util.exponential که می تواند exponentiate هر رفت و آمد cirq.PauliSum اشیاء:
def v_theta(qubits):
"""Prepares a circuit that generates V(\theta)."""
ref_paulis = [
cirq.X(q0) * cirq.X(q1) + \
cirq.Y(q0) * cirq.Y(q1) + \
cirq.Z(q0) * cirq.Z(q1) for q0, q1 in zip(qubits, qubits[1:])
]
exp_symbols = list(sympy.symbols('ref_0:'+str(len(ref_paulis))))
return tfq.util.exponential(ref_paulis, exp_symbols), exp_symbols
بررسی این مدار ممکن است با نگاه کردن به آن کمی سختتر باشد، اما همچنان میتوانید یک مورد دو کیوبیتی را بررسی کنید تا ببینید چه اتفاقی میافتد:
test_circuit, test_symbols = v_theta(cirq.GridQubit.rect(1, 2))
print(f'Symbols found in circuit:{test_symbols}')
SVGCircuit(test_circuit)
Symbols found in circuit:[ref_0]
اکنون تمام بلوکهای ساختمانی مورد نیاز برای قرار دادن مدارهای رمزگذاری کامل خود را در اختیار دارید:
def prepare_pqk_circuits(qubits, classical_source, n_trotter=10):
"""Prepare the pqk feature circuits around a dataset."""
n_qubits = len(qubits)
n_points = len(classical_source)
# Prepare random single qubit rotation wall.
random_rots = np.random.uniform(-2, 2, size=(n_qubits, 3))
initial_U = single_qubit_wall(qubits, random_rots)
# Prepare parametrized V
V_circuit, symbols = v_theta(qubits)
exp_circuit = cirq.Circuit(V_circuit for t in range(n_trotter))
# Convert to `tf.Tensor`
initial_U_tensor = tfq.convert_to_tensor([initial_U])
initial_U_splat = tf.tile(initial_U_tensor, [n_points])
full_circuits = tfq.layers.AddCircuit()(
initial_U_splat, append=exp_circuit)
# Replace placeholders in circuits with values from `classical_source`.
return tfq.resolve_parameters(
full_circuits, tf.convert_to_tensor([str(x) for x in symbols]),
tf.convert_to_tensor(classical_source*(n_qubits/3)/n_trotter))
چند کیوبیت را انتخاب کنید و مدارهای رمزگذاری داده را آماده کنید:
qubits = cirq.GridQubit.rect(1, DATASET_DIM + 1)
q_x_train_circuits = prepare_pqk_circuits(qubits, x_train)
q_x_test_circuits = prepare_pqk_circuits(qubits, x_test)
بعد، محاسبه PQK ویژگی های در 1-RDM از مدارهای مجموعه داده فوق بر اساس و ذخیره نتایج در rdm ، یک tf.Tensor با شکل [n_points, n_qubits, 3] . این نوشته را در rdm[i][j][k] = \(\langle \psi_i | OP^k_j | \psi_i \rangle\) که در آن i شاخص بیش از datapoints، j شاخص بیش از کیوبیت و k شاخص بیش از \(\lbrace \hat{X}, \hat{Y}, \hat{Z} \rbrace\) .
def get_pqk_features(qubits, data_batch):
"""Get PQK features based on above construction."""
ops = [[cirq.X(q), cirq.Y(q), cirq.Z(q)] for q in qubits]
ops_tensor = tf.expand_dims(tf.reshape(tfq.convert_to_tensor(ops), -1), 0)
batch_dim = tf.gather(tf.shape(data_batch), 0)
ops_splat = tf.tile(ops_tensor, [batch_dim, 1])
exp_vals = tfq.layers.Expectation()(data_batch, operators=ops_splat)
rdm = tf.reshape(exp_vals, [batch_dim, len(qubits), -1])
return rdm
x_train_pqk = get_pqk_features(qubits, q_x_train_circuits)
x_test_pqk = get_pqk_features(qubits, q_x_test_circuits)
print('New PQK training dataset has shape:', x_train_pqk.shape)
print('New PQK testing dataset has shape:', x_test_pqk.shape)
New PQK training dataset has shape: (1000, 11, 3) New PQK testing dataset has shape: (200, 11, 3)
2.2 برچسب زدن مجدد بر اساس ویژگی های PQK
حالا که شما این ویژگی کوانتومی تولید شده در x_train_pqk و x_test_pqk ، آن هم به دوباره برچسب مجموعه داده است. برای رسیدن به حداکثر جدائی بین کوانتومی و عملکرد کلاسیک شما می توانید دوباره برچسب مجموعه داده را بر اساس اطلاعات طیف در یافت x_train_pqk و x_test_pqk .
def compute_kernel_matrix(vecs, gamma):
"""Computes d[i][j] = e^ -gamma * (vecs[i] - vecs[j]) ** 2 """
scaled_gamma = gamma / (
tf.cast(tf.gather(tf.shape(vecs), 1), tf.float32) * tf.math.reduce_std(vecs))
return scaled_gamma * tf.einsum('ijk->ij',(vecs[:,None,:] - vecs) ** 2)
def get_spectrum(datapoints, gamma=1.0):
"""Compute the eigenvalues and eigenvectors of the kernel of datapoints."""
KC_qs = compute_kernel_matrix(datapoints, gamma)
S, V = tf.linalg.eigh(KC_qs)
S = tf.math.abs(S)
return S, V
S_pqk, V_pqk = get_spectrum(
tf.reshape(tf.concat([x_train_pqk, x_test_pqk], 0), [-1, len(qubits) * 3]))
S_original, V_original = get_spectrum(
tf.cast(tf.concat([x_train, x_test], 0), tf.float32), gamma=0.005)
print('Eigenvectors of pqk kernel matrix:', V_pqk)
print('Eigenvectors of original kernel matrix:', V_original)
Eigenvectors of pqk kernel matrix: tf.Tensor( [[-2.09569391e-02 1.05973557e-02 2.16634180e-02 ... 2.80352887e-02 1.55521873e-02 2.82677952e-02] [-2.29303762e-02 4.66355234e-02 7.91163836e-03 ... -6.14174758e-04 -7.07804322e-01 2.85902526e-02] [-1.77853629e-02 -3.00758495e-03 -2.55225878e-02 ... -2.40783971e-02 2.11018627e-03 2.69009806e-02] ... [ 6.05797209e-02 1.32483775e-02 2.69536003e-02 ... -1.38843581e-02 3.05043962e-02 3.85345481e-02] [ 6.33309558e-02 -3.04112374e-03 9.77444276e-03 ... 7.48321265e-02 3.42793856e-03 3.67484428e-02] [ 5.86028099e-02 5.84433973e-03 2.64811981e-03 ... 2.82612257e-02 -3.80136147e-02 3.29943895e-02]], shape=(1200, 1200), dtype=float32) Eigenvectors of original kernel matrix: tf.Tensor( [[ 0.03835681 0.0283473 -0.01169789 ... 0.02343717 0.0211248 0.03206972] [-0.04018159 0.00888097 -0.01388255 ... 0.00582427 0.717551 0.02881948] [-0.0166719 0.01350376 -0.03663862 ... 0.02467175 -0.00415936 0.02195409] ... [-0.03015648 -0.01671632 -0.01603392 ... 0.00100583 -0.00261221 0.02365689] [ 0.0039777 -0.04998879 -0.00528336 ... 0.01560401 -0.04330755 0.02782002] [-0.01665728 -0.00818616 -0.0432341 ... 0.00088256 0.00927396 0.01875088]], shape=(1200, 1200), dtype=float32)
اکنون همه چیزهایی را که برای برچسب گذاری مجدد مجموعه داده نیاز دارید در اختیار دارید! اکنون می توانید برای درک بهتر نحوه به حداکثر رساندن جداسازی عملکرد هنگام برچسب گذاری مجدد مجموعه داده، با فلوچارت مشورت کنید:
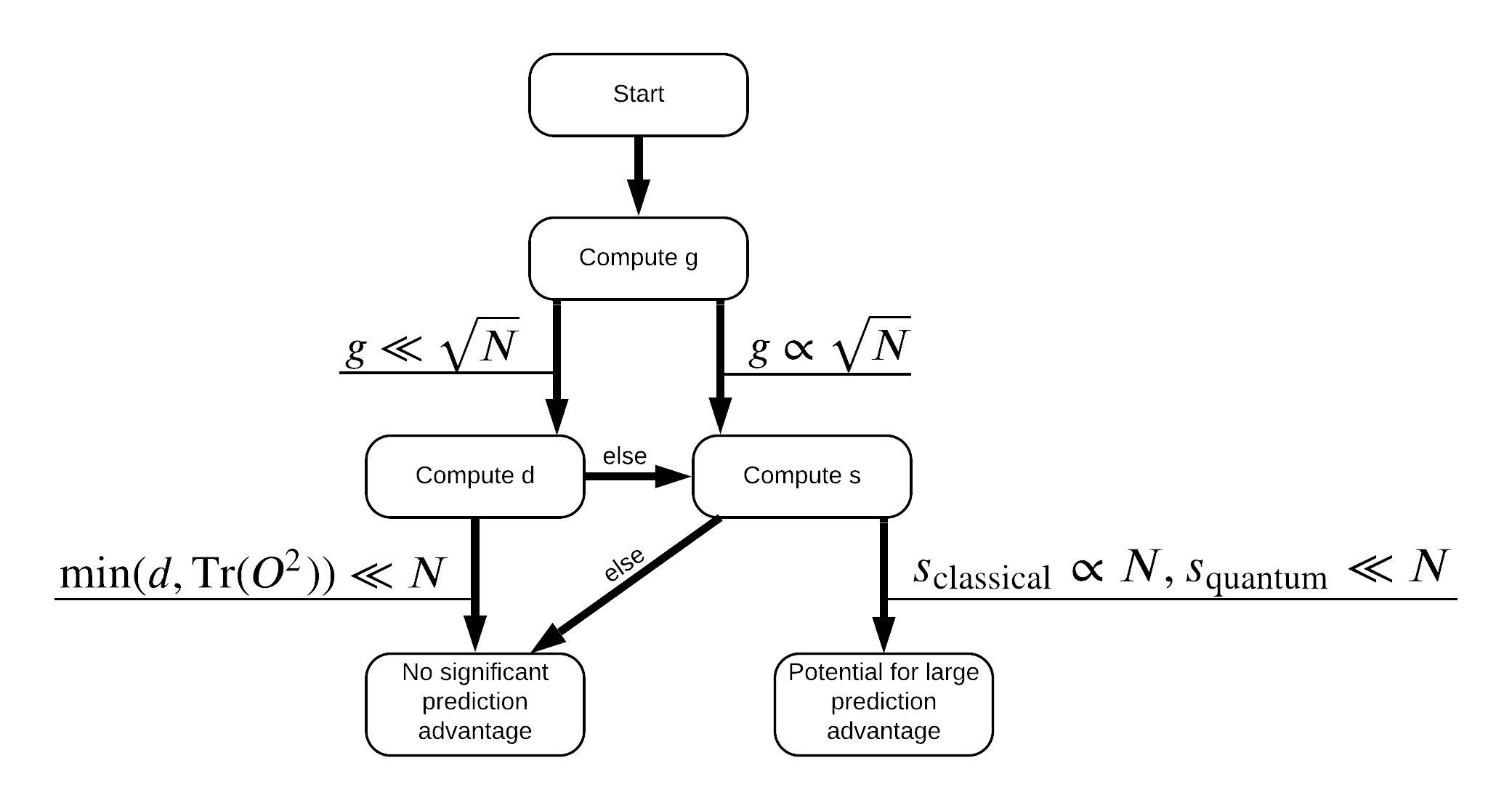
به منظور به حداکثر رساندن جدائی بین کوانتومی و مدل های کلاسیک، شما تلاش خواهد کرد برای به حداکثر رساندن تفاوت هندسی بین مجموعه داده اصلی و PQK ویژگی های هسته ماتریس \(g(K_1 || K_2) = \sqrt{ || \sqrt{K_2} K_1^{-1} \sqrt{K_2} || _\infty}\) با استفاده از S_pqk, V_pqk و S_original, V_original . مقدار زیادی از \(g\) تضمین می کند که شما در ابتدا به سمت راست در پایین فلوچارت به سمت یک مزیت پیش بینی در مورد کوانتومی حرکت می کند.
def get_stilted_dataset(S, V, S_2, V_2, lambdav=1.1):
"""Prepare new labels that maximize geometric distance between kernels."""
S_diag = tf.linalg.diag(S ** 0.5)
S_2_diag = tf.linalg.diag(S_2 / (S_2 + lambdav) ** 2)
scaling = S_diag @ tf.transpose(V) @ \
V_2 @ S_2_diag @ tf.transpose(V_2) @ \
V @ S_diag
# Generate new lables using the largest eigenvector.
_, vecs = tf.linalg.eig(scaling)
new_labels = tf.math.real(
tf.einsum('ij,j->i', tf.cast(V @ S_diag, tf.complex64), vecs[-1])).numpy()
# Create new labels and add some small amount of noise.
final_y = new_labels > np.median(new_labels)
noisy_y = (final_y ^ (np.random.uniform(size=final_y.shape) > 0.95))
return noisy_y
y_relabel = get_stilted_dataset(S_pqk, V_pqk, S_original, V_original)
y_train_new, y_test_new = y_relabel[:N_TRAIN], y_relabel[N_TRAIN:]
3. مقایسه مدل ها
اکنون که مجموعه داده خود را آماده کرده اید، زمان مقایسه عملکرد مدل فرا رسیده است. شما دو شبکه عصبی پیشخور کوچک ایجاد و مقایسه عملکرد در هنگام به آنها داده شده دسترسی به PQK ویژگی های در یافت x_train_pqk .
3.1 مدل پیشرفته PQK را ایجاد کنید
با استفاده از استاندارد tf.keras ویژگی های کتابخانه شما هم اکنون می توانید ایجاد و یک قطار یک مدل در x_train_pqk و y_train_new datapoints:
#docs_infra: no_execute
def create_pqk_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[len(qubits) * 3,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
pqk_model = create_pqk_model()
pqk_model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.003),
metrics=['accuracy'])
pqk_model.summary()
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 32) 1088 _________________________________________________________________ dense_1 (Dense) (None, 16) 528 _________________________________________________________________ dense_2 (Dense) (None, 1) 17 ================================================================= Total params: 1,633 Trainable params: 1,633 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
pqk_history = pqk_model.fit(tf.reshape(x_train_pqk, [N_TRAIN, -1]),
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(tf.reshape(x_test_pqk, [N_TEST, -1]), y_test_new))
3.2 یک مدل کلاسیک ایجاد کنید
مشابه کد بالا، اکنون میتوانید یک مدل کلاسیک نیز ایجاد کنید که به ویژگیهای PQK در مجموعه دادههای استیل دار شما دسترسی ندارد. این مدل می تواند با استفاده از آموزش دیده x_train و y_label_new .
#docs_infra: no_execute
def create_fair_classical_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[DATASET_DIM,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.03),
metrics=['accuracy'])
model.summary()
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_3 (Dense) (None, 32) 352 _________________________________________________________________ dense_4 (Dense) (None, 16) 528 _________________________________________________________________ dense_5 (Dense) (None, 1) 17 ================================================================= Total params: 897 Trainable params: 897 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
classical_history = model.fit(x_train,
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(x_test, y_test_new))
3.3 مقایسه عملکرد
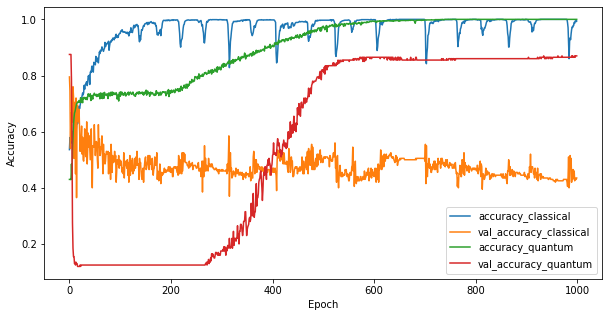
اکنون که دو مدل را آموزش دادهاید، میتوانید به سرعت شکافهای عملکردی در دادههای اعتبارسنجی بین این دو را رسم کنید. به طور معمول هر دو مدل به دقت بیش از 0.9 در داده های آموزشی دست خواهند یافت. با این حال، در دادههای اعتبارسنجی مشخص میشود که فقط اطلاعات موجود در ویژگیهای PQK برای تعمیم مدل به نمونههای دیده نشده کافی است.
#docs_infra: no_execute
plt.figure(figsize=(10,5))
plt.plot(classical_history.history['accuracy'], label='accuracy_classical')
plt.plot(classical_history.history['val_accuracy'], label='val_accuracy_classical')
plt.plot(pqk_history.history['accuracy'], label='accuracy_quantum')
plt.plot(pqk_history.history['val_accuracy'], label='val_accuracy_quantum')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x7f6d846ecee0>
4. نتیجه گیری مهم
چند نتیجه مهم شما می توانید از این و قرعه کشی وجود دارد MNIST آزمایش:
خیلی بعید است که مدل های کوانتومی امروزی عملکرد مدل کلاسیک را بر روی داده های کلاسیک شکست دهند. به خصوص در مجموعه داده های کلاسیک امروزی که می توانند بیش از یک میلیون نقطه داده داشته باشند.
فقط به این دلیل که داده ها ممکن است از یک مدار کوانتومی شبیه سازی کلاسیک سخت به دست بیایند، لزوما یادگیری داده ها را برای یک مدل کلاسیک سخت نمی کند.
مجموعههای داده (در نهایت ماهیت کوانتومی) که یادگیری آنها برای مدلهای کوانتومی آسان و یادگیری مدلهای کلاسیک دشوار است، بدون توجه به معماری مدل یا الگوریتمهای آموزشی مورد استفاده، وجود دارند.
