 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar libreta Descargar libreta |
Este tutorial presenta los codificadores automáticos con tres ejemplos: los conceptos básicos, la eliminación de ruido de la imagen y la detección de anomalías.
Un codificador automático es un tipo especial de red neuronal que está entrenada para copiar su entrada a su salida. Por ejemplo, dada una imagen de un dígito escrito a mano, un codificador automático primero codifica la imagen en una representación latente de menor dimensión y luego decodifica la representación latente de nuevo en una imagen. Un codificador automático aprende a comprimir los datos mientras minimiza el error de reconstrucción.
Para obtener más información sobre los codificadores automáticos, considere leer el capítulo 14 de Deep Learning de Ian Goodfellow, Yoshua Bengio y Aaron Courville.
Importar TensorFlow y otras bibliotecas
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
Cargue el conjunto de datos
Para comenzar, entrenará el codificador automático básico utilizando el conjunto de datos Fashion MNIST. Cada imagen en este conjunto de datos tiene 28x28 píxeles.
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
print (x_train.shape)
print (x_test.shape)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz 32768/29515 [=================================] - 0s 0us/step 40960/29515 [=========================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz 26427392/26421880 [==============================] - 0s 0us/step 26435584/26421880 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz 16384/5148 [===============================================================================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz 4423680/4422102 [==============================] - 0s 0us/step 4431872/4422102 [==============================] - 0s 0us/step (60000, 28, 28) (10000, 28, 28)
Primer ejemplo: codificador automático básico

Defina un codificador automático con dos capas densas: un encoder , que comprime las imágenes en un vector latente de 64 dimensiones, y un decoder , que reconstruye la imagen original a partir del espacio latente.
Para definir su modelo, utilice la API de subclases de modelos de Keras .
latent_dim = 64
class Autoencoder(Model):
def __init__(self, latent_dim):
super(Autoencoder, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential([
layers.Flatten(),
layers.Dense(latent_dim, activation='relu'),
])
self.decoder = tf.keras.Sequential([
layers.Dense(784, activation='sigmoid'),
layers.Reshape((28, 28))
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Autoencoder(latent_dim)
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
Entrene el modelo usando x_train como entrada y como destino. El encoder aprenderá a comprimir el conjunto de datos de 784 dimensiones al espacio latente, y el decoder aprenderá a reconstruir las imágenes originales. .
autoencoder.fit(x_train, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test, x_test))
Epoch 1/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0243 - val_loss: 0.0140 Epoch 2/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0116 - val_loss: 0.0106 Epoch 3/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0100 - val_loss: 0.0098 Epoch 4/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0094 - val_loss: 0.0094 Epoch 5/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0092 - val_loss: 0.0092 Epoch 6/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0090 - val_loss: 0.0091 Epoch 7/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0090 - val_loss: 0.0090 Epoch 8/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0089 - val_loss: 0.0090 Epoch 9/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0088 - val_loss: 0.0089 Epoch 10/10 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0088 - val_loss: 0.0089 <keras.callbacks.History at 0x7ff1d35df550>
Ahora que el modelo está entrenado, probémoslo codificando y decodificando imágenes del conjunto de prueba.
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i])
plt.title("original")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i])
plt.title("reconstructed")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

Segundo ejemplo: eliminación de ruido de la imagen

También se puede entrenar un codificador automático para eliminar el ruido de las imágenes. En la siguiente sección, creará una versión ruidosa del conjunto de datos Fashion MNIST aplicando ruido aleatorio a cada imagen. Luego entrenará un codificador automático utilizando la imagen ruidosa como entrada y la imagen original como objetivo.
Volvamos a importar el conjunto de datos para omitir las modificaciones realizadas anteriormente.
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train[..., tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape)
(60000, 28, 28, 1)
Agregar ruido aleatorio a las imágenes
noise_factor = 0.2
x_train_noisy = x_train + noise_factor * tf.random.normal(shape=x_train.shape)
x_test_noisy = x_test + noise_factor * tf.random.normal(shape=x_test.shape)
x_train_noisy = tf.clip_by_value(x_train_noisy, clip_value_min=0., clip_value_max=1.)
x_test_noisy = tf.clip_by_value(x_test_noisy, clip_value_min=0., clip_value_max=1.)
Trace las imágenes ruidosas.
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
plt.show()

Definir un codificador automático convolucional
En este ejemplo, entrenará un codificador automático convolucional utilizando capas Conv2D en el encoder y capas Conv2DTranspose en el decoder .
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2),
layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3, 3), activation='sigmoid', padding='same')])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
autoencoder.fit(x_train_noisy, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test_noisy, x_test))
Epoch 1/10 1875/1875 [==============================] - 8s 3ms/step - loss: 0.0169 - val_loss: 0.0107 Epoch 2/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0095 - val_loss: 0.0086 Epoch 3/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0082 - val_loss: 0.0080 Epoch 4/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0078 - val_loss: 0.0077 Epoch 5/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0076 - val_loss: 0.0075 Epoch 6/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0074 - val_loss: 0.0074 Epoch 7/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0073 - val_loss: 0.0073 Epoch 8/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0072 - val_loss: 0.0072 Epoch 9/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0071 - val_loss: 0.0071 Epoch 10/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0070 - val_loss: 0.0071 <keras.callbacks.History at 0x7ff1c45a31d0>
Echemos un vistazo a un resumen del codificador. Observe cómo se reducen las muestras de las imágenes de 28x28 a 7x7.
autoencoder.encoder.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 14, 14, 16) 160
conv2d_1 (Conv2D) (None, 7, 7, 8) 1160
=================================================================
Total params: 1,320
Trainable params: 1,320
Non-trainable params: 0
_________________________________________________________________
El decodificador vuelve a muestrear las imágenes de 7x7 a 28x28.
autoencoder.decoder.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_transpose (Conv2DTra (None, 14, 14, 8) 584
nspose)
conv2d_transpose_1 (Conv2DT (None, 28, 28, 16) 1168
ranspose)
conv2d_2 (Conv2D) (None, 28, 28, 1) 145
=================================================================
Total params: 1,897
Trainable params: 1,897
Non-trainable params: 0
_________________________________________________________________
Trazado tanto de las imágenes con ruido como de las imágenes sin ruido producidas por el codificador automático.
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original + noise
ax = plt.subplot(2, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
bx = plt.subplot(2, n, i + n + 1)
plt.title("reconstructed")
plt.imshow(tf.squeeze(decoded_imgs[i]))
plt.gray()
bx.get_xaxis().set_visible(False)
bx.get_yaxis().set_visible(False)
plt.show()

Tercer ejemplo: Detección de anomalías
Descripción general
En este ejemplo, entrenará un codificador automático para detectar anomalías en el conjunto de datos ECG5000 . Este conjunto de datos contiene 5000 electrocardiogramas , cada uno con 140 puntos de datos. Utilizará una versión simplificada del conjunto de datos, donde cada ejemplo se ha etiquetado como 0 (correspondiente a un ritmo anormal) o 1 (correspondiente a un ritmo normal). Le interesa identificar los ritmos anormales.
¿Cómo detectará anomalías utilizando un codificador automático? Recuerde que un codificador automático está entrenado para minimizar el error de reconstrucción. Entrenará un codificador automático solo en los ritmos normales, luego lo usará para reconstruir todos los datos. Nuestra hipótesis es que los ritmos anormales tendrán mayor error de reconstrucción. A continuación, clasificará un ritmo como anomalía si el error de reconstrucción supera un umbral fijo.
Cargar datos de ECG
El conjunto de datos que utilizará se basa en uno de timeseriesclassification.com .
# Download the dataset
dataframe = pd.read_csv('http://storage.googleapis.com/download.tensorflow.org/data/ecg.csv', header=None)
raw_data = dataframe.values
dataframe.head()
# The last element contains the labels
labels = raw_data[:, -1]
# The other data points are the electrocadriogram data
data = raw_data[:, 0:-1]
train_data, test_data, train_labels, test_labels = train_test_split(
data, labels, test_size=0.2, random_state=21
)
Normalice los datos a [0,1] .
min_val = tf.reduce_min(train_data)
max_val = tf.reduce_max(train_data)
train_data = (train_data - min_val) / (max_val - min_val)
test_data = (test_data - min_val) / (max_val - min_val)
train_data = tf.cast(train_data, tf.float32)
test_data = tf.cast(test_data, tf.float32)
Entrenará el codificador automático usando solo los ritmos normales, que están etiquetados en este conjunto de datos como 1 . Separar los ritmos normales de los ritmos anormales.
train_labels = train_labels.astype(bool)
test_labels = test_labels.astype(bool)
normal_train_data = train_data[train_labels]
normal_test_data = test_data[test_labels]
anomalous_train_data = train_data[~train_labels]
anomalous_test_data = test_data[~test_labels]
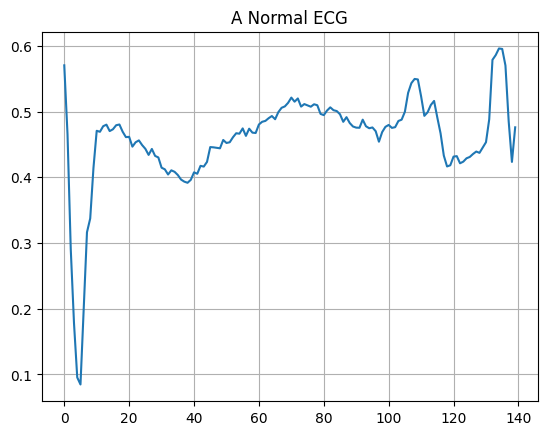
Trazar un ECG normal.
plt.grid()
plt.plot(np.arange(140), normal_train_data[0])
plt.title("A Normal ECG")
plt.show()
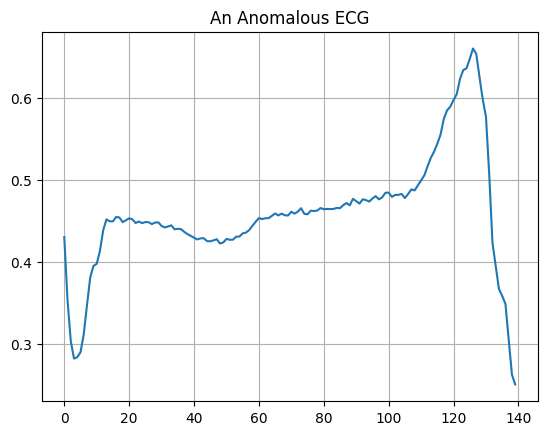
Trazar un ECG anómalo.
plt.grid()
plt.plot(np.arange(140), anomalous_train_data[0])
plt.title("An Anomalous ECG")
plt.show()
Construye el modelo
class AnomalyDetector(Model):
def __init__(self):
super(AnomalyDetector, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Dense(32, activation="relu"),
layers.Dense(16, activation="relu"),
layers.Dense(8, activation="relu")])
self.decoder = tf.keras.Sequential([
layers.Dense(16, activation="relu"),
layers.Dense(32, activation="relu"),
layers.Dense(140, activation="sigmoid")])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = AnomalyDetector()
autoencoder.compile(optimizer='adam', loss='mae')
Tenga en cuenta que el codificador automático se entrena utilizando solo los ECG normales, pero se evalúa utilizando el conjunto de prueba completo.
history = autoencoder.fit(normal_train_data, normal_train_data,
epochs=20,
batch_size=512,
validation_data=(test_data, test_data),
shuffle=True)
Epoch 1/20 5/5 [==============================] - 1s 33ms/step - loss: 0.0576 - val_loss: 0.0531 Epoch 2/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0552 - val_loss: 0.0514 Epoch 3/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0519 - val_loss: 0.0499 Epoch 4/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0483 - val_loss: 0.0475 Epoch 5/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0445 - val_loss: 0.0451 Epoch 6/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0409 - val_loss: 0.0432 Epoch 7/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0377 - val_loss: 0.0415 Epoch 8/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0348 - val_loss: 0.0401 Epoch 9/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0319 - val_loss: 0.0388 Epoch 10/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0293 - val_loss: 0.0378 Epoch 11/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0273 - val_loss: 0.0369 Epoch 12/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0259 - val_loss: 0.0361 Epoch 13/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0249 - val_loss: 0.0354 Epoch 14/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0239 - val_loss: 0.0346 Epoch 15/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0230 - val_loss: 0.0340 Epoch 16/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0222 - val_loss: 0.0335 Epoch 17/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0215 - val_loss: 0.0331 Epoch 18/20 5/5 [==============================] - 0s 9ms/step - loss: 0.0211 - val_loss: 0.0331 Epoch 19/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0208 - val_loss: 0.0329 Epoch 20/20 5/5 [==============================] - 0s 8ms/step - loss: 0.0206 - val_loss: 0.0327
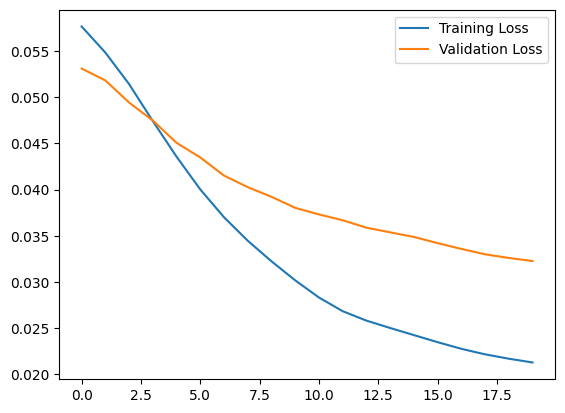
plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
<matplotlib.legend.Legend at 0x7ff1d339b790>
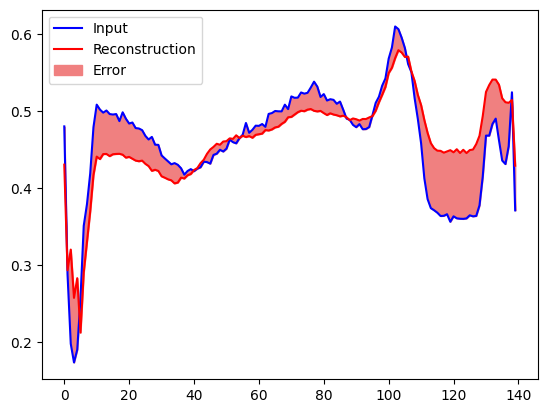
Pronto clasificará un ECG como anómalo si el error de reconstrucción es mayor que una desviación estándar de los ejemplos de entrenamiento normales. Primero, tracemos un ECG normal del conjunto de entrenamiento, la reconstrucción después de que el codificador automático lo codifique y decodifique, y el error de reconstrucción.
encoded_data = autoencoder.encoder(normal_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(normal_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], normal_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
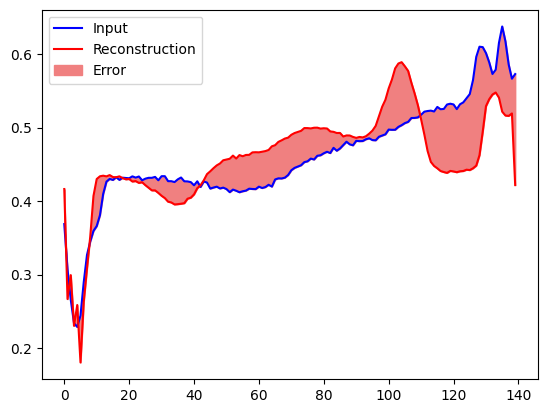
Cree una trama similar, esta vez para un ejemplo de prueba anómalo.
encoded_data = autoencoder.encoder(anomalous_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(anomalous_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], anomalous_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
Detectar anomalías
Detecte anomalías calculando si la pérdida de reconstrucción es mayor que un umbral fijo. En este tutorial, calculará el error promedio promedio para ejemplos normales del conjunto de entrenamiento, luego clasificará ejemplos futuros como anómalos si el error de reconstrucción es mayor que una desviación estándar del conjunto de entrenamiento.
Trazar el error de reconstrucción en ECG normales del conjunto de entrenamiento
reconstructions = autoencoder.predict(normal_train_data)
train_loss = tf.keras.losses.mae(reconstructions, normal_train_data)
plt.hist(train_loss[None,:], bins=50)
plt.xlabel("Train loss")
plt.ylabel("No of examples")
plt.show()

Elija un valor de umbral que sea una desviación estándar por encima de la media.
threshold = np.mean(train_loss) + np.std(train_loss)
print("Threshold: ", threshold)
Threshold: 0.03241627
Si examina el error de reconstrucción de los ejemplos anómalos en el conjunto de prueba, notará que la mayoría tiene un error de reconstrucción mayor que el umbral. Al variar el umbral, puede ajustar la precisión y la recuperación de su clasificador.
reconstructions = autoencoder.predict(anomalous_test_data)
test_loss = tf.keras.losses.mae(reconstructions, anomalous_test_data)
plt.hist(test_loss[None, :], bins=50)
plt.xlabel("Test loss")
plt.ylabel("No of examples")
plt.show()

Clasifique un ECG como una anomalía si el error de reconstrucción es mayor que el umbral.
def predict(model, data, threshold):
reconstructions = model(data)
loss = tf.keras.losses.mae(reconstructions, data)
return tf.math.less(loss, threshold)
def print_stats(predictions, labels):
print("Accuracy = {}".format(accuracy_score(labels, predictions)))
print("Precision = {}".format(precision_score(labels, predictions)))
print("Recall = {}".format(recall_score(labels, predictions)))
preds = predict(autoencoder, test_data, threshold)
print_stats(preds, test_labels)
Accuracy = 0.944 Precision = 0.9921875 Recall = 0.9071428571428571
Próximos pasos
Para obtener más información sobre la detección de anomalías con codificadores automáticos, consulte este excelente ejemplo interactivo creado con TensorFlow.js por Victor Dibia. Para un caso de uso del mundo real, puede obtener información sobre cómo Airbus detecta anomalías en los datos de telemetría de la ISS mediante TensorFlow. Para obtener más información sobre los conceptos básicos, considere leer esta publicación de blog de François Chollet. Para obtener más detalles, consulte el capítulo 14 de Deep Learning de Ian Goodfellow, Yoshua Bengio y Aaron Courville.
