 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar libreta Descargar libreta |
Este tutorial es una introducción a la previsión de series temporales con TensorFlow. Construye algunos estilos diferentes de modelos, incluidas las redes neuronales convolucionales y recurrentes (CNN y RNN).
Esto se cubre en dos partes principales, con subsecciones:
- Pronóstico para un solo paso de tiempo:
- Una sola característica.
- Todas las características.
- Pronostique varios pasos:
- Disparo único: haga todas las predicciones a la vez.
- Autorregresivo: haga una predicción a la vez y envíe la salida al modelo.
Configuración
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
El conjunto de datos meteorológicos
Este tutorial utiliza un conjunto de datos de series temporales meteorológicas registrado por el Instituto Max Planck de Biogeoquímica .
Este conjunto de datos contiene 14 características diferentes, como la temperatura del aire, la presión atmosférica y la humedad. Estos se recopilaron cada 10 minutos a partir de 2003. Para mayor eficiencia, utilizará solo los datos recopilados entre 2009 y 2016. Esta sección del conjunto de datos fue preparada por François Chollet para su libro Aprendizaje profundo con Python .
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
Este tutorial solo se ocupará de las predicciones por hora , así que comience submuestreando los datos en intervalos de 10 minutos a intervalos de una hora:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
Echemos un vistazo a los datos. Aquí están las primeras filas:
df.head()
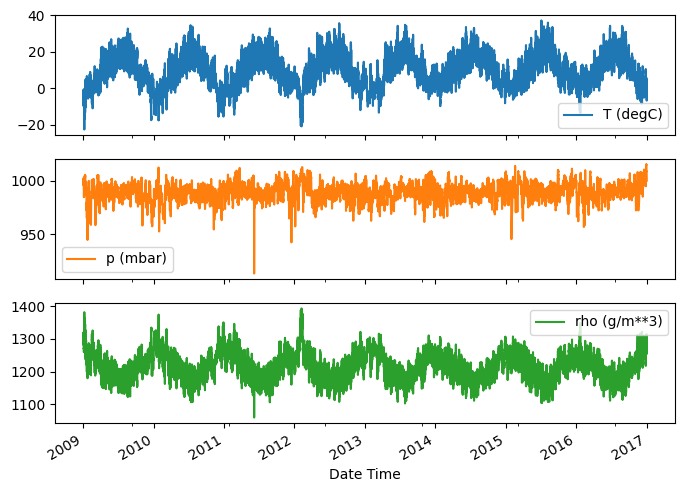
Aquí está la evolución de algunas características a lo largo del tiempo:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
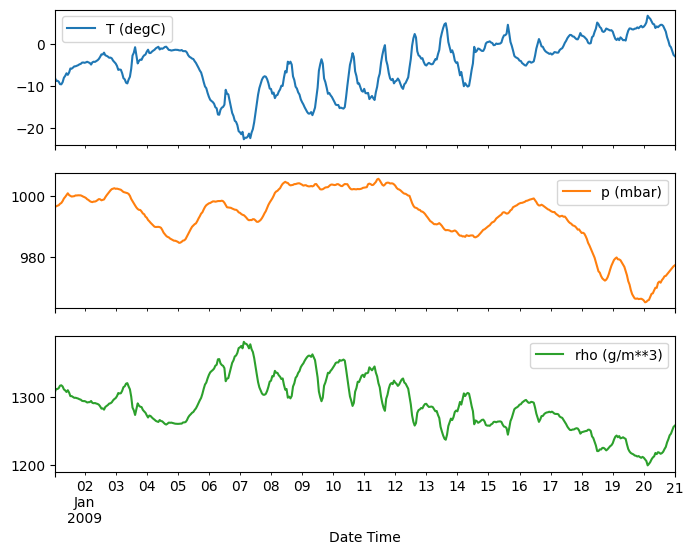
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
Inspeccionar y limpiar
A continuación, mire las estadísticas del conjunto de datos:
df.describe().transpose()
Velocidad del viento
Una cosa que debe destacarse es el valor min de la velocidad del viento ( wv (m/s) ) y el valor máximo ( max. wv (m/s) ) columnas. Es probable que este -9999 sea erróneo.
Hay una columna de dirección del viento separada, por lo que la velocidad debe ser mayor que cero ( >=0 ). Reemplázalo con ceros:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
Ingeniería de características
Antes de sumergirse en la creación de un modelo, es importante comprender sus datos y asegurarse de que está pasando los datos del modelo con el formato adecuado.
Viento
La última columna de los datos, wd (deg) , da la dirección del viento en unidades de grados. Los ángulos no son buenas entradas de modelo: 360° y 0° deben estar cerca uno del otro y envolverse sin problemas. La dirección no debería importar si el viento no sopla.
En este momento, la distribución de los datos del viento se ve así:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
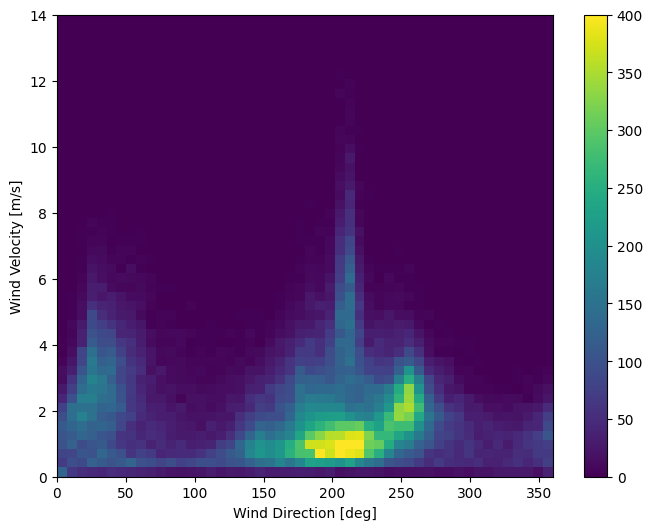
Pero esto será más fácil de interpretar para el modelo si convierte las columnas de dirección y velocidad del viento en un vector de viento:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
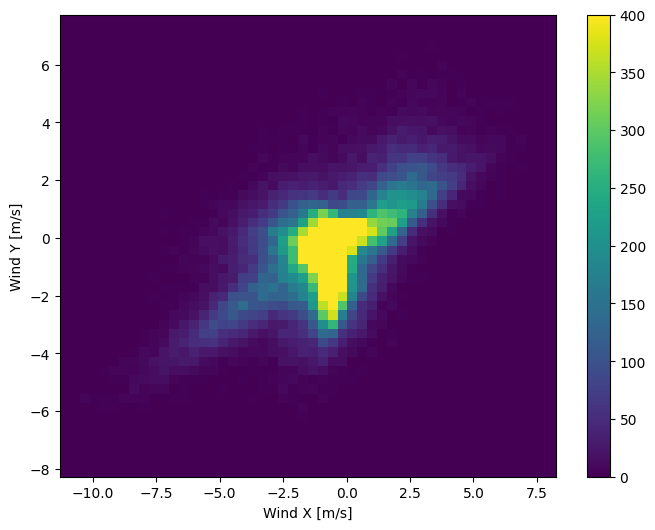
La distribución de los vectores de viento es mucho más simple para que el modelo la interprete correctamente:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
Hora
De manera similar, la columna Date Time es muy útil, pero no en este formato de cadena. Comience por convertirlo a segundos:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
Similar a la dirección del viento, el tiempo en segundos no es una entrada de modelo útil. Al ser datos meteorológicos, tiene una clara periodicidad diaria y anual. Hay muchas maneras de lidiar con la periodicidad.
Puede obtener señales utilizables mediante el uso de transformaciones de seno y coseno para borrar las señales de "Hora del día" y "Hora del año":
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
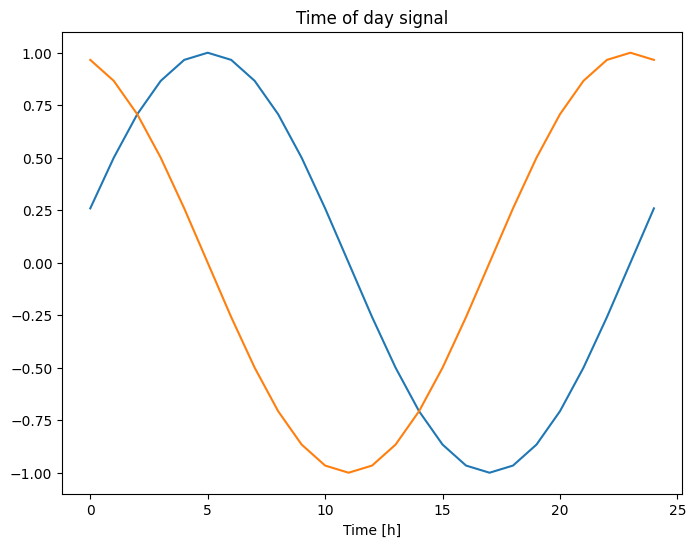
Esto le da al modelo acceso a las características de frecuencia más importantes. En este caso, sabía de antemano qué frecuencias eran importantes.
Si no tiene esa información, puede determinar qué frecuencias son importantes extrayendo características con Fast Fourier Transform . Para verificar las suposiciones, aquí está el tf.signal.rfft de la temperatura a lo largo del tiempo. Tenga en cuenta los picos obvios en frecuencias cercanas a 1/year y 1/day :
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
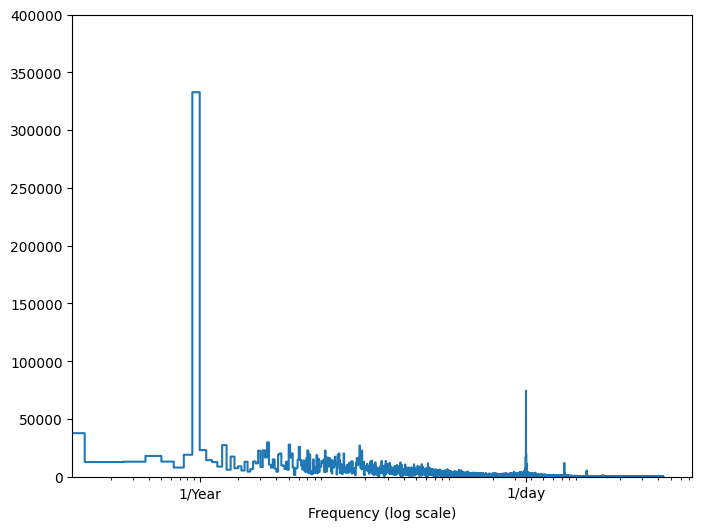
dividir los datos
Utilizará una división (70%, 20%, 10%) para los conjuntos de entrenamiento, validación y prueba. Tenga en cuenta que los datos no se barajan aleatoriamente antes de dividirlos. Esto es por dos razones:
- Garantiza que aún es posible dividir los datos en ventanas de muestras consecutivas.
- Garantiza que los resultados de la validación/prueba sean más realistas y se evalúen sobre los datos recopilados después de entrenar el modelo.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
Normalizar los datos
Es importante escalar las características antes de entrenar una red neuronal. La normalización es una forma común de hacer esta escala: restar la media y dividir por la desviación estándar de cada característica.
La media y la desviación estándar solo deben calcularse utilizando los datos de entrenamiento para que los modelos no tengan acceso a los valores en los conjuntos de validación y prueba.
También es discutible que el modelo no debería tener acceso a valores futuros en el conjunto de entrenamiento durante el entrenamiento, y que esta normalización debería hacerse usando promedios móviles. Ese no es el enfoque de este tutorial, y los conjuntos de validación y prueba aseguran que obtenga métricas (algo) honestas. Entonces, en aras de la simplicidad, este tutorial usa un promedio simple.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
Ahora, eche un vistazo a la distribución de las características. Algunas características tienen colas largas, pero no hay errores obvios como el valor de velocidad del viento -9999 .
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

Ventanas de datos
Los modelos de este tutorial harán un conjunto de predicciones basadas en una ventana de muestras consecutivas de los datos.
Las características principales de las ventanas de entrada son:
- El ancho (número de pasos de tiempo) de las ventanas de entrada y etiqueta.
- El tiempo de compensación entre ellos.
- Qué funciones se utilizan como entradas, etiquetas o ambas.
Este tutorial crea una variedad de modelos (incluidos los modelos Linear, DNN, CNN y RNN) y los usa para ambos:
- Predicciones de salida única y de salida múltiple .
- Predicciones de un solo paso de tiempo y de varios pasos de tiempo .
Esta sección se enfoca en implementar la ventana de datos para que pueda reutilizarse para todos esos modelos.
Según la tarea y el tipo de modelo, es posible que desee generar una variedad de ventanas de datos. Aquí hay unos ejemplos:
Por ejemplo, para hacer una sola predicción 24 horas en el futuro, con 24 horas de historial, puede definir una ventana como esta:
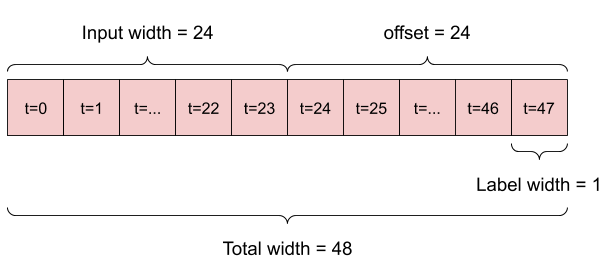
Un modelo que hace una predicción una hora en el futuro, dadas seis horas de historial, necesitaría una ventana como esta:

El resto de esta sección define una clase WindowGenerator . Esta clase puede:
- Maneje los índices y las compensaciones como se muestra en los diagramas anteriores.
- Dividir ventanas de características en pares
(features, labels). - Trace el contenido de las ventanas resultantes.
- Genere eficientemente lotes de estas ventanas a partir de los datos de entrenamiento, evaluación y prueba, utilizando
tf.data.Datasets.
1. Índices y compensaciones
Comience creando la clase WindowGenerator . El método __init__ incluye toda la lógica necesaria para los índices de entrada y etiqueta.
También toma los DataFrames de entrenamiento, evaluación y prueba como entrada. Estos se convertirán a tf.data.Dataset s de Windows más adelante.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
Aquí está el código para crear las 2 ventanas que se muestran en los diagramas al comienzo de esta sección:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. Dividir
Dada una lista de entradas consecutivas, el método split_window las convertirá en una ventana de entradas y una ventana de etiquetas.
El ejemplo w2 que definió anteriormente se dividirá así:
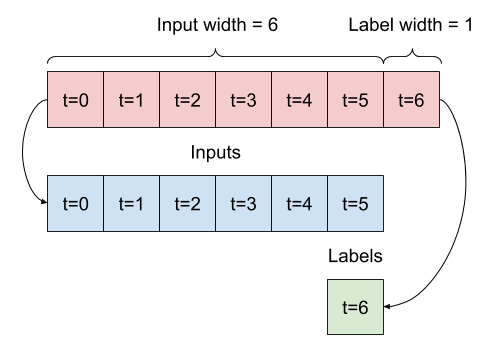
Este diagrama no muestra el eje de features de los datos, pero esta función split_window también maneja las label_columns , por lo que puede usarse tanto para los ejemplos de salida única como de salida múltiple.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
Pruébalo:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
Por lo general, los datos en TensorFlow se empaquetan en matrices donde el índice más externo se encuentra en los ejemplos (la dimensión "por lotes"). Los índices intermedios son las dimensiones de "tiempo" o "espacio" (ancho, alto). Los índices más internos son las características.
El código anterior tomó un lote de tres ventanas de 7 pasos de tiempo con 19 características en cada paso de tiempo. Los divide en un lote de entradas de función de 19 pasos de 6 tiempos y una etiqueta de función de paso 1 de 1 vez. La etiqueta solo tiene una función porque WindowGenerator se inicializó con label_columns=['T (degC)'] . Inicialmente, este tutorial creará modelos que predicen etiquetas de salida únicas.
3. Trama
Aquí hay un método de trazado que permite una visualización simple de la ventana dividida:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
Esta gráfica alinea las entradas, las etiquetas y (posteriormente) las predicciones en función del tiempo al que hace referencia el elemento:
w2.plot()
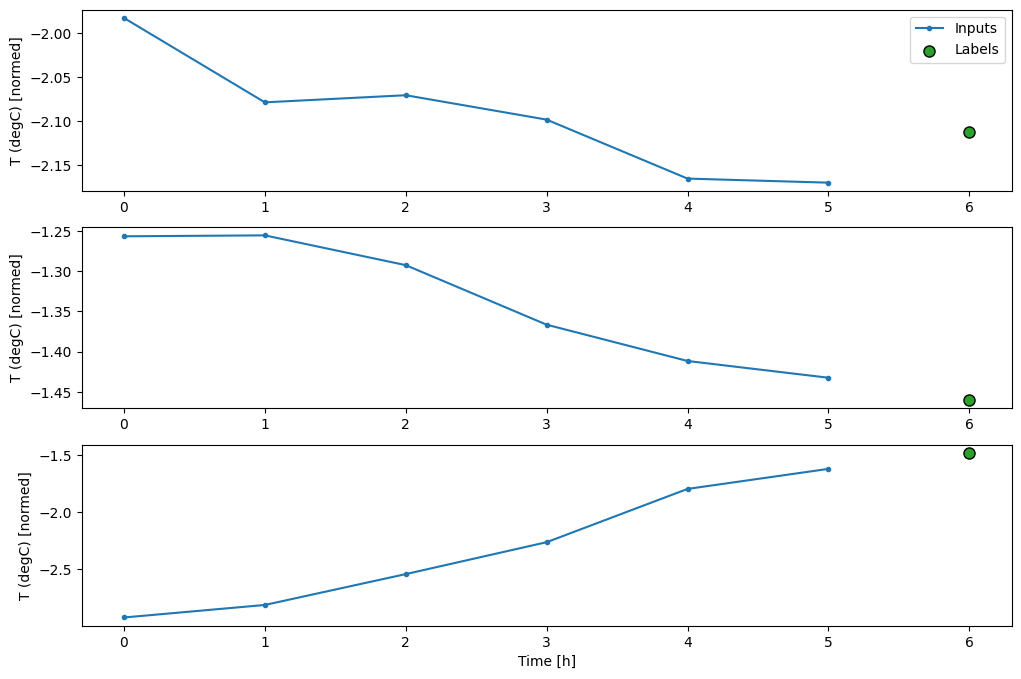
Puede trazar las otras columnas, pero la configuración w2 de la ventana de ejemplo solo tiene etiquetas para la columna T (degC) .
w2.plot(plot_col='p (mbar)')
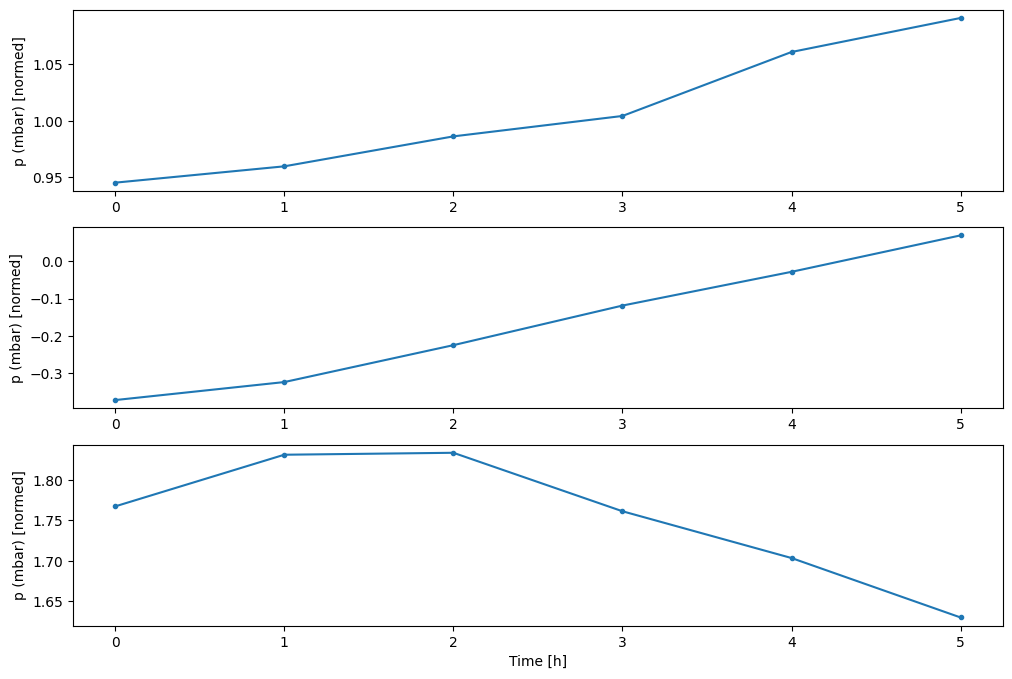
4. Crear tf.data.Dataset s
Finalmente, este método make_dataset tomará un DataFrame de serie temporal y lo convertirá en un tf.data.Dataset de (input_window, label_window) usando la función tf.keras.utils.timeseries_dataset_from_array :
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
El objeto WindowGenerator contiene datos de entrenamiento, validación y prueba.
Agregue propiedades para acceder a ellas como tf.data.Dataset s utilizando el método make_dataset que definió anteriormente. Además, agregue un lote de ejemplo estándar para facilitar el acceso y el trazado:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
Ahora, el objeto WindowGenerator le da acceso a los objetos tf.data.Dataset , para que pueda iterar fácilmente sobre los datos.
La propiedad Dataset.element_spec le indica la estructura, los tipos de datos y las formas de los elementos del conjunto de datos.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
Iterar sobre un conjunto de Dataset produce lotes concretos:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
Modelos de un solo paso
El modelo más simple que puede crear a partir de este tipo de datos es el que predice el valor de una sola característica: 1 paso de tiempo (una hora) hacia el futuro basándose únicamente en las condiciones actuales.
Entonces, comience por construir modelos para predecir el valor T (degC) una hora en el futuro.
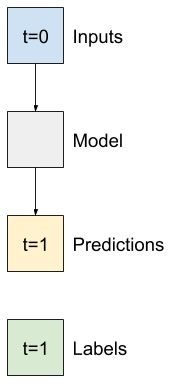
Configure un objeto WindowGenerator para producir estos pares de un solo paso (input, label) :
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
El objeto de window crea tf.data.Dataset s a partir de los conjuntos de entrenamiento, validación y prueba, lo que le permite iterar fácilmente sobre lotes de datos.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
Base
Antes de construir un modelo entrenable, sería bueno tener una línea base de rendimiento como punto de comparación con los modelos posteriores más complicados.
Esta primera tarea es predecir la temperatura una hora en el futuro, dado el valor actual de todas las características. Los valores actuales incluyen la temperatura actual.
Entonces, comience con un modelo que solo devuelva la temperatura actual como predicción, prediciendo "Sin cambios". Esta es una línea de base razonable ya que la temperatura cambia lentamente. Por supuesto, esta línea de base funcionará menos bien si hace una predicción más adelante en el futuro.
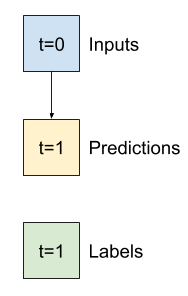
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
Crea una instancia y evalúa este modelo:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
Eso imprimió algunas métricas de rendimiento, pero eso no le da una idea de qué tan bien está funcionando el modelo.
WindowGenerator tiene un método de trazado, pero los trazados no serán muy interesantes con una sola muestra.
Por lo tanto, cree un WindowGenerator más amplio que genere ventanas 24 horas de entradas y etiquetas consecutivas a la vez. La nueva variable wide_window no cambia la forma en que opera el modelo. El modelo aún hace predicciones una hora en el futuro en función de un solo paso de tiempo de entrada. Aquí, el eje de time actúa como el eje de batch : cada predicción se realiza de forma independiente sin interacción entre los pasos de tiempo:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
Esta ventana expandida se puede pasar directamente al mismo modelo de baseline de base sin ningún cambio de código. Esto es posible porque las entradas y las etiquetas tienen la misma cantidad de pasos de tiempo, y la línea de base solo reenvía la entrada a la salida:
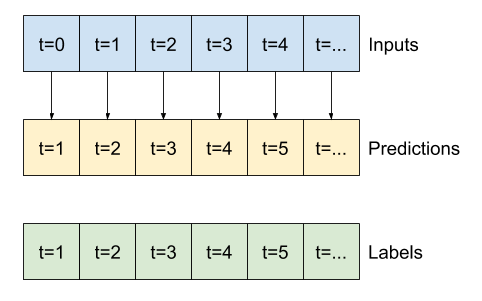
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
Al trazar las predicciones del modelo de referencia, observe que son simplemente las etiquetas desplazadas a la derecha una hora:
wide_window.plot(baseline)
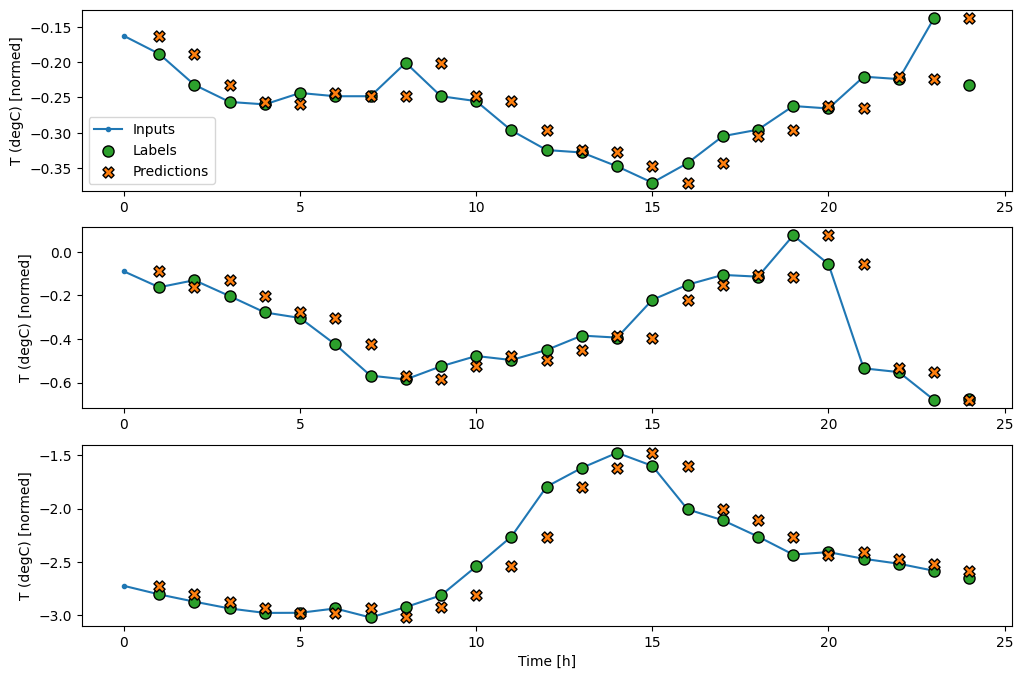
En las gráficas anteriores de tres ejemplos, el modelo de un solo paso se ejecuta en el transcurso de 24 horas. Esto merece alguna explicación:
- La línea azul
Inputsmuestra la temperatura de entrada en cada paso de tiempo. El modelo recibe todas las características, este gráfico solo muestra la temperatura. - Los puntos de
Labelsverdes muestran el valor de predicción objetivo. Estos puntos se muestran en el tiempo de predicción, no en el tiempo de entrada. Es por eso que el rango de etiquetas se desplaza 1 paso en relación con las entradas. - Las cruces naranjas de
Predictionsson las predicciones del modelo para cada paso de tiempo de salida. Si el modelo predijera perfectamente, las predicciones aterrizarían directamente en lasLabels.
Modelo lineal
El modelo entrenable más simple que puede aplicar a esta tarea es insertar una transformación lineal entre la entrada y la salida. En este caso, la salida de un paso de tiempo solo depende de ese paso:

Una capa tf.keras.layers.Dense sin conjunto de activation es un modelo lineal. La capa solo transforma el último eje de los datos de (batch, time, inputs) a (batch, time, units) ; se aplica de forma independiente a cada artículo en el batch y los ejes de time .
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
Este tutorial entrena muchos modelos, así que empaque el procedimiento de entrenamiento en una función:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
Entrene el modelo y evalúe su rendimiento:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
Al igual que el modelo de línea de baseline , el modelo lineal se puede llamar en lotes de ventanas anchas. Usado de esta manera, el modelo hace un conjunto de predicciones independientes en pasos de tiempo consecutivos. El eje de time actúa como otro eje de batch . No hay interacciones entre las predicciones en cada paso de tiempo.
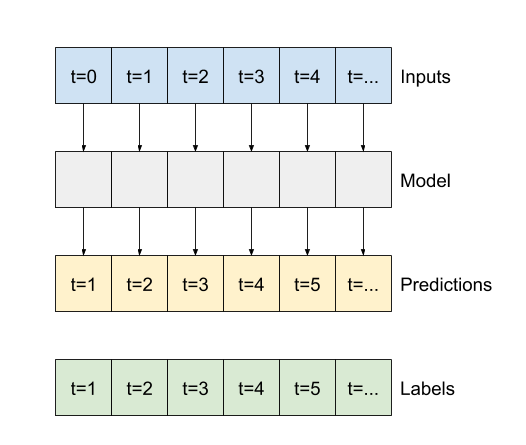
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
Aquí está la trama de sus predicciones de ejemplo en wide_window , observe cómo en muchos casos la predicción es claramente mejor que simplemente devolver la temperatura de entrada, pero en algunos casos es peor:
wide_window.plot(linear)
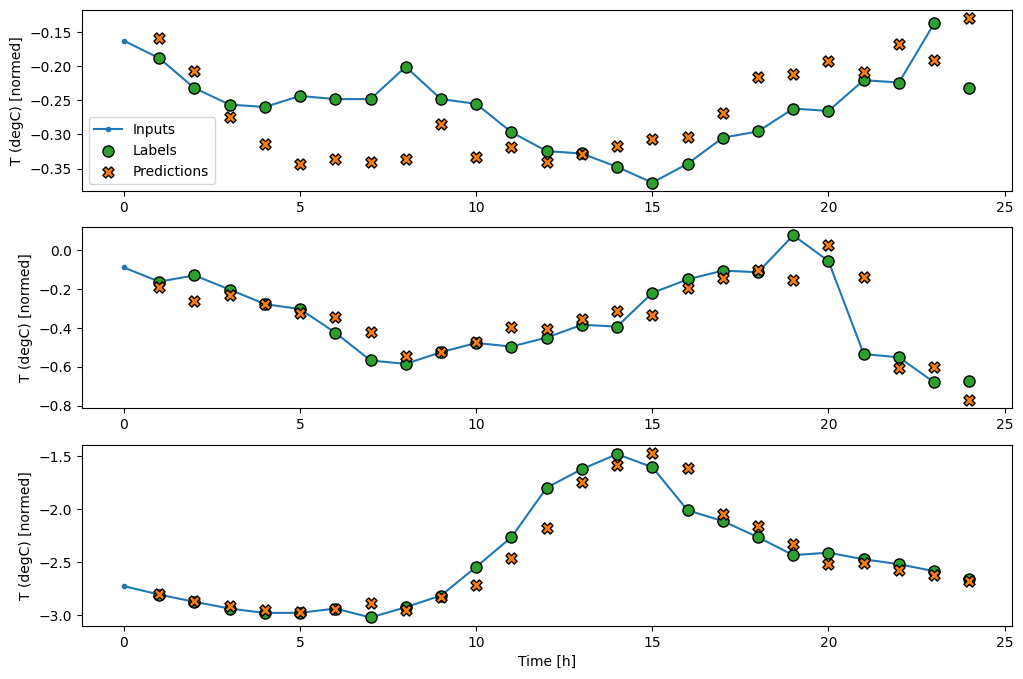
Una ventaja de los modelos lineales es que son relativamente simples de interpretar. Puede extraer los pesos de la capa y visualizar el peso asignado a cada entrada:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
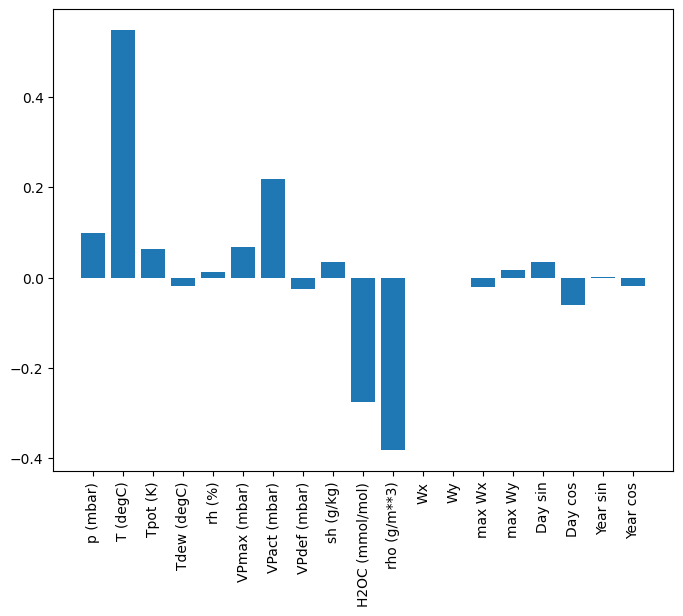
A veces, el modelo ni siquiera coloca el mayor peso en la entrada T (degC) . Este es uno de los riesgos de la inicialización aleatoria.
Denso
Antes de aplicar modelos que realmente operan en múltiples pasos de tiempo, vale la pena comprobar el rendimiento de modelos de paso de entrada única más profundos y potentes.
Aquí hay un modelo similar al modelo linear , excepto que apila varias capas Dense entre la entrada y la salida:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
denso de varios pasos
Un modelo de paso de tiempo único no tiene contexto para los valores actuales de sus entradas. No puede ver cómo las características de entrada cambian con el tiempo. Para abordar este problema, el modelo necesita acceso a varios pasos de tiempo al hacer predicciones:
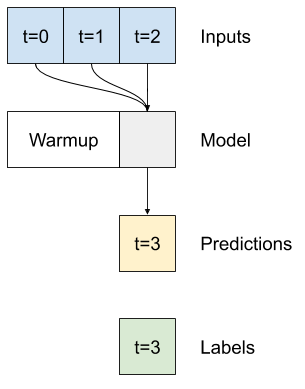
Los modelos de baseline , linear y dense manejaron cada paso de tiempo de forma independiente. Aquí el modelo tomará múltiples pasos de tiempo como entrada para producir una única salida.
Cree un WindowGenerator que produzca lotes de entradas de tres horas y etiquetas de una hora:
Tenga en cuenta que el parámetro de shift de la Window es relativo al final de las dos ventanas.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
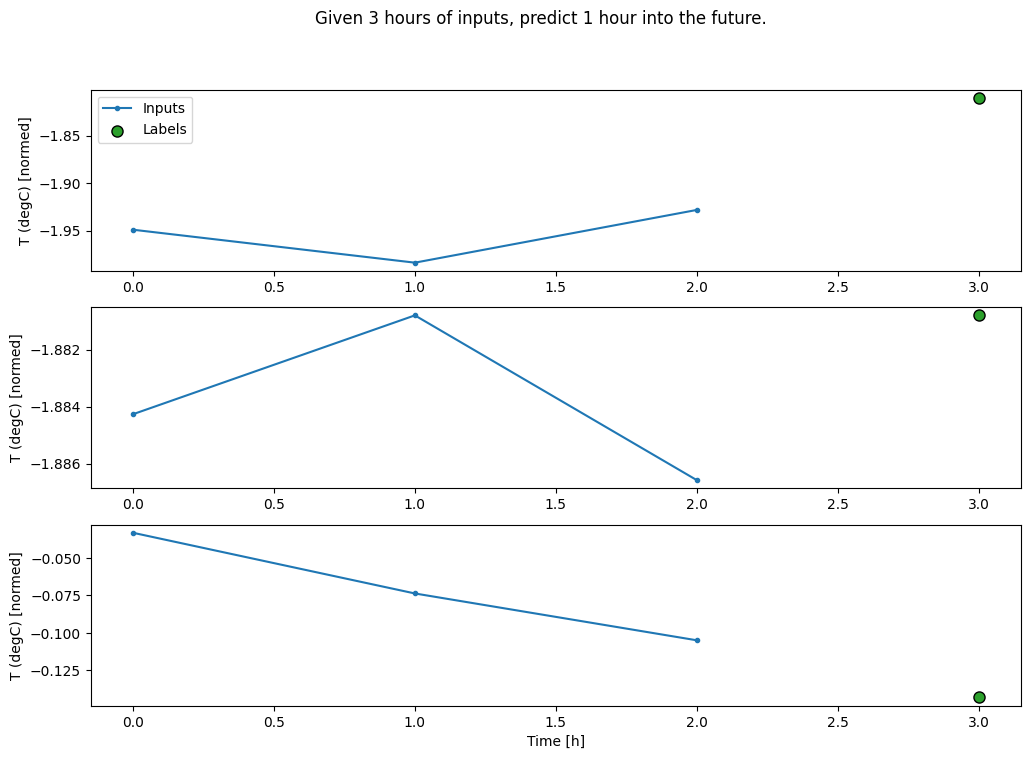
Puede entrenar un modelo dense en una ventana de múltiples pasos de entrada agregando tf.keras.layers.Flatten como la primera capa del modelo:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
conv_window.plot(multi_step_dense)
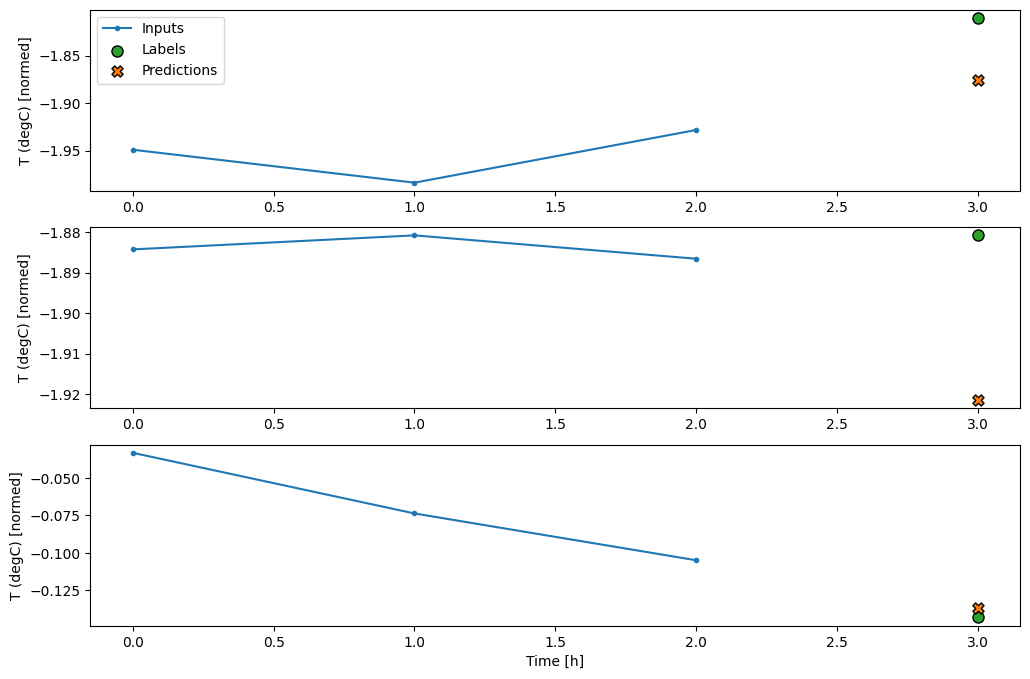
La principal desventaja de este enfoque es que el modelo resultante solo se puede ejecutar en ventanas de entrada que tengan exactamente esta forma.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
Los modelos convolucionales de la siguiente sección solucionan este problema.
Red neuronal de convolución
Una capa de convolución ( tf.keras.layers.Conv1D ) también toma varios pasos de tiempo como entrada para cada predicción.
A continuación se muestra el mismo modelo que multi_step_dense , reescrito con una convolución.
Tenga en cuenta los cambios:
- El
tf.keras.layers.Flatteny el primertf.keras.layers.Densese reemplazan por untf.keras.layers.Conv1D. - El
tf.keras.layers.Reshapeya no es necesario ya que la convolución mantiene el eje del tiempo en su salida.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
Ejecútelo en un lote de ejemplo para verificar que el modelo produce resultados con la forma esperada:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
Entrénelo y evalúelo en conv_window y debería brindar un rendimiento similar al modelo multi_step_dense .
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
La diferencia entre este conv_model y el modelo multi_step_dense es que el modelo conv_model se puede ejecutar en entradas de cualquier longitud. La capa convolucional se aplica a una ventana deslizante de entradas:
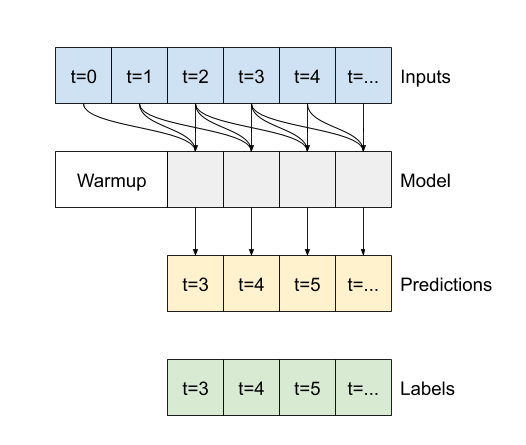
Si lo ejecuta en una entrada más amplia, produce una salida más amplia:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
Tenga en cuenta que la salida es más corta que la entrada. Para que el entrenamiento o el trazado funcionen, necesita que las etiquetas y la predicción tengan la misma longitud. Por lo tanto, construya un WindowGenerator para producir ventanas anchas con algunos pasos de tiempo de entrada adicionales para que la etiqueta y la longitud de la predicción coincidan:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
Ahora, puede trazar las predicciones del modelo en una ventana más amplia. Tenga en cuenta los 3 pasos de tiempo de entrada antes de la primera predicción. Cada predicción aquí se basa en los 3 pasos de tiempo anteriores:
wide_conv_window.plot(conv_model)
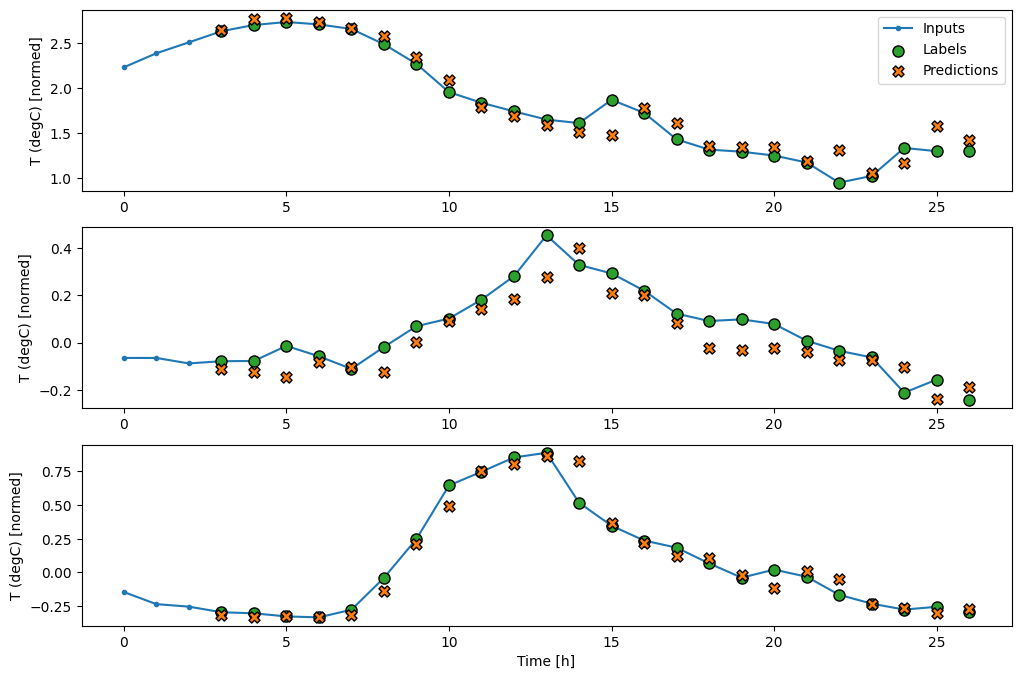
Red neuronal recurrente
Una red neuronal recurrente (RNN) es un tipo de red neuronal muy adecuada para datos de series temporales. Los RNN procesan una serie de tiempo paso a paso, manteniendo un estado interno de un paso de tiempo a otro.
Puede obtener más información en el tutorial Generación de texto con RNN y la guía Redes neuronales recurrentes (RNN) con Keras .
En este tutorial, usará una capa RNN llamada Memoria a largo plazo a corto plazo ( tf.keras.layers.LSTM ).
Un argumento constructor importante para todas las capas de Keras RNN, como tf.keras.layers.LSTM , es el argumento return_sequences . Esta configuración puede configurar la capa de una de dos maneras:
- Si es
False, el valor predeterminado, la capa solo devuelve la salida del paso de tiempo final, dando tiempo al modelo para calentar su estado interno antes de hacer una sola predicción:
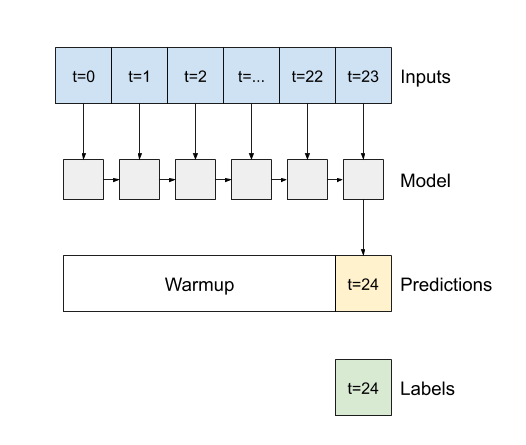
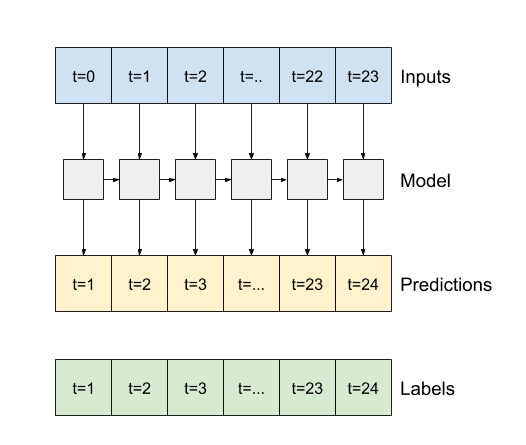
- Si es
True, la capa devuelve una salida para cada entrada. Esto es útil para:- Apilamiento de capas RNN.
- Entrenamiento de un modelo en múltiples pasos de tiempo simultáneamente.
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
Con return_sequences=True , el modelo se puede entrenar con 24 horas de datos a la vez.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
wide_window.plot(lstm_model)
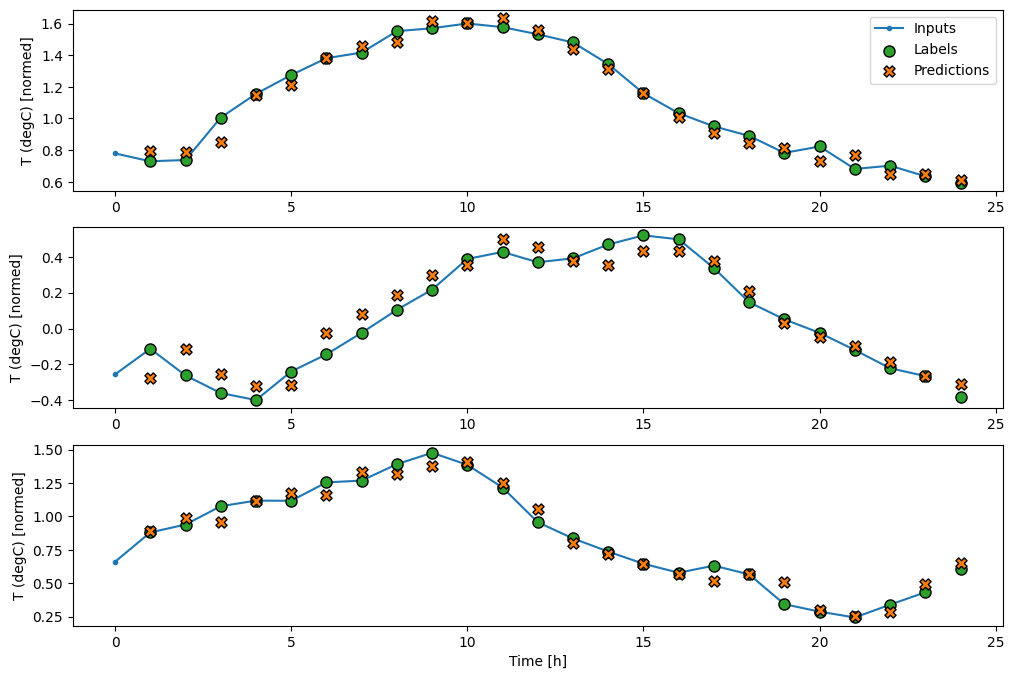
Rendimiento
Con este conjunto de datos, por lo general, cada uno de los modelos funciona un poco mejor que el anterior:
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()
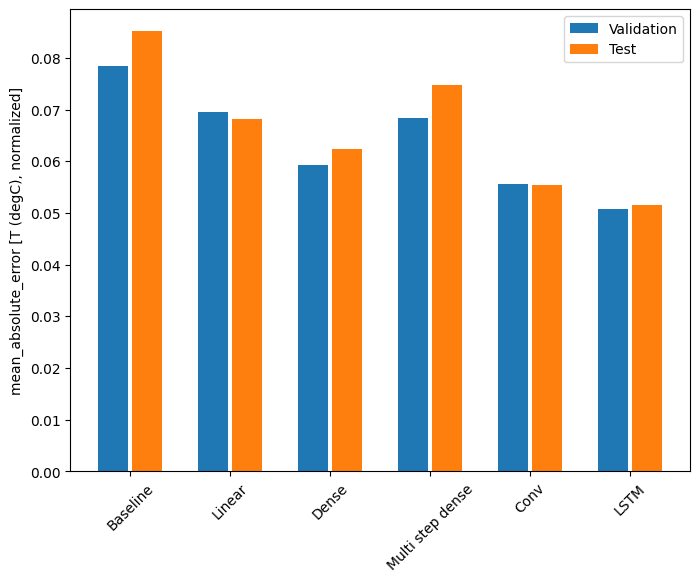
for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
Modelos multisalida
Hasta ahora, todos los modelos predijeron una sola característica de salida, T (degC) , para un solo paso de tiempo.
Todos estos modelos se pueden convertir para predecir múltiples funciones simplemente cambiando la cantidad de unidades en la capa de salida y ajustando las ventanas de entrenamiento para incluir todas las funciones en las labels ( example_labels ):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
Tenga en cuenta arriba que el eje de features de las etiquetas ahora tiene la misma profundidad que las entradas, en lugar de 1 .
Base
Aquí se puede usar el mismo modelo de línea de base ( Baseline ), pero esta vez repitiendo todas las funciones en lugar de seleccionar un label_index específico:
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
Denso
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
RNN
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
Avanzado: Conexiones residuales
El modelo Baseline de antes aprovechó el hecho de que la secuencia no cambia drásticamente de un paso de tiempo a otro. Todos los modelos entrenados en este tutorial hasta ahora se inicializaron aleatoriamente y luego tuvieron que aprender que la salida es un pequeño cambio con respecto al paso de tiempo anterior.
Si bien puede solucionar este problema con una inicialización cuidadosa, es más sencillo integrarlo en la estructura del modelo.
Es común en el análisis de series de tiempo construir modelos que en lugar de predecir el siguiente valor, predicen cómo cambiará el valor en el siguiente paso de tiempo. De manera similar, las redes residuales, o ResNets, en el aprendizaje profundo se refieren a arquitecturas en las que cada capa se suma al resultado acumulativo del modelo.
Así se aprovecha el saber que el cambio debe ser pequeño.
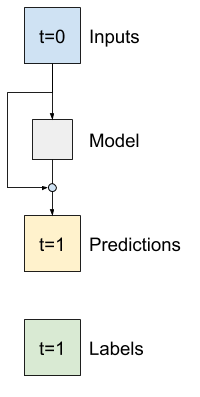
Esencialmente, esto inicializa el modelo para que coincida con la línea de Baseline . Para esta tarea, ayuda a que los modelos converjan más rápido, con un rendimiento ligeramente mejor.
Este enfoque se puede usar junto con cualquier modelo discutido en este tutorial.
Aquí, se está aplicando al modelo LSTM, tenga en cuenta el uso de tf.initializers.zeros para garantizar que los cambios iniciales previstos sean pequeños y no dominen la conexión residual. Aquí no hay problemas de ruptura de simetría para los gradientes, ya que los zeros solo se usan en la última capa.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
Rendimiento
Este es el rendimiento general de estos modelos de múltiples salidas.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
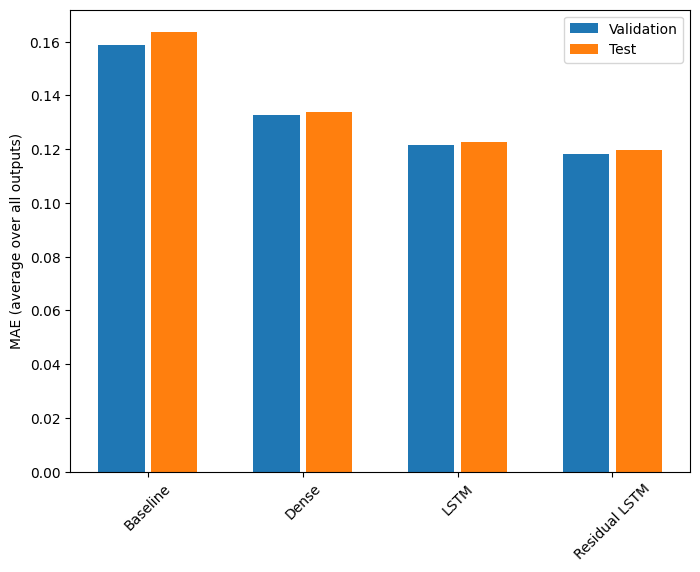
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
Los rendimientos anteriores se promedian en todos los resultados del modelo.
Modelos de varios pasos
Tanto el modelo de salida única como el de salida múltiple en las secciones anteriores hicieron predicciones de un solo paso de tiempo , una hora en el futuro.
Esta sección analiza cómo expandir estos modelos para hacer predicciones de múltiples pasos de tiempo .
En una predicción de varios pasos, el modelo necesita aprender a predecir un rango de valores futuros. Por lo tanto, a diferencia de un modelo de un solo paso, donde solo se predice un único punto futuro, un modelo de varios pasos predice una secuencia de valores futuros.
Hay dos enfoques aproximados para esto:
- Predicciones de disparo único donde se predice la serie temporal completa a la vez.
- Predicciones autorregresivas donde el modelo solo hace predicciones de un solo paso y su salida se retroalimenta como su entrada.
En esta sección, todos los modelos predecirán todas las características en todos los pasos de tiempo de salida .
Para el modelo de varios pasos, los datos de entrenamiento nuevamente consisten en muestras por hora. Sin embargo, aquí, los modelos aprenderán a predecir 24 horas en el futuro, dadas las 24 horas del pasado.
Aquí hay un objeto de Window que genera estos segmentos a partir del conjunto de datos:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
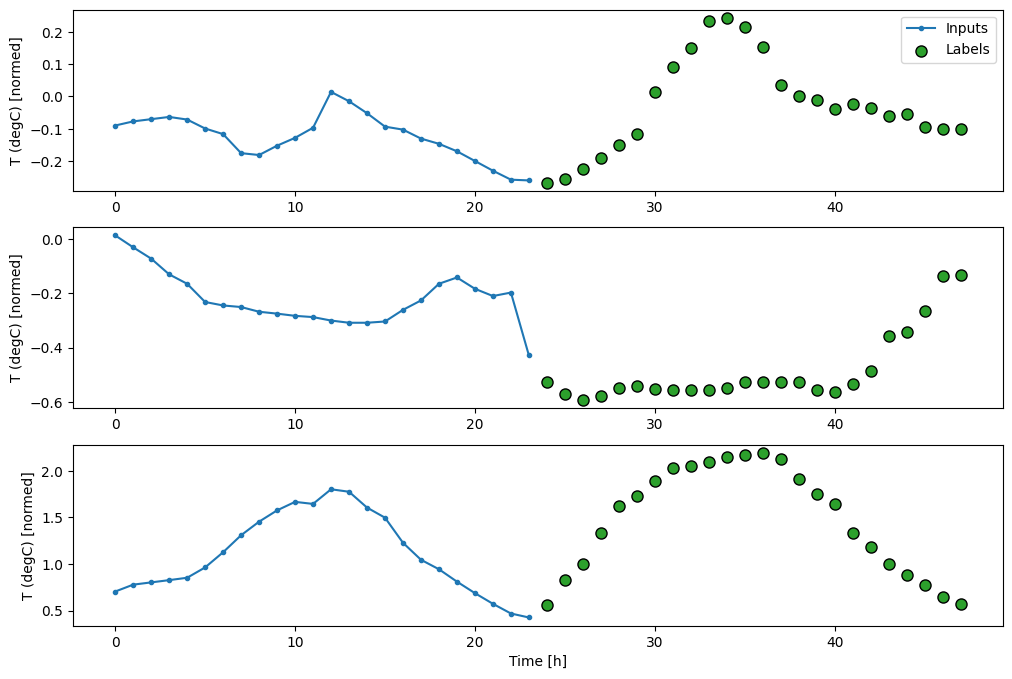
Líneas base
Una línea de base simple para esta tarea es repetir el último paso de tiempo de entrada para el número requerido de pasos de tiempo de salida:
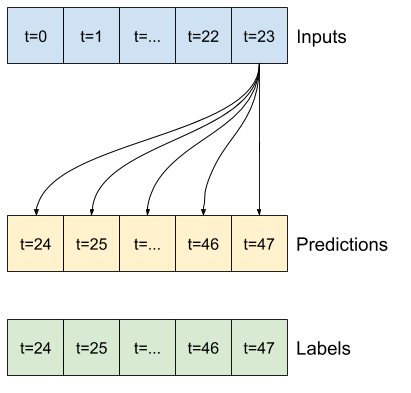
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007
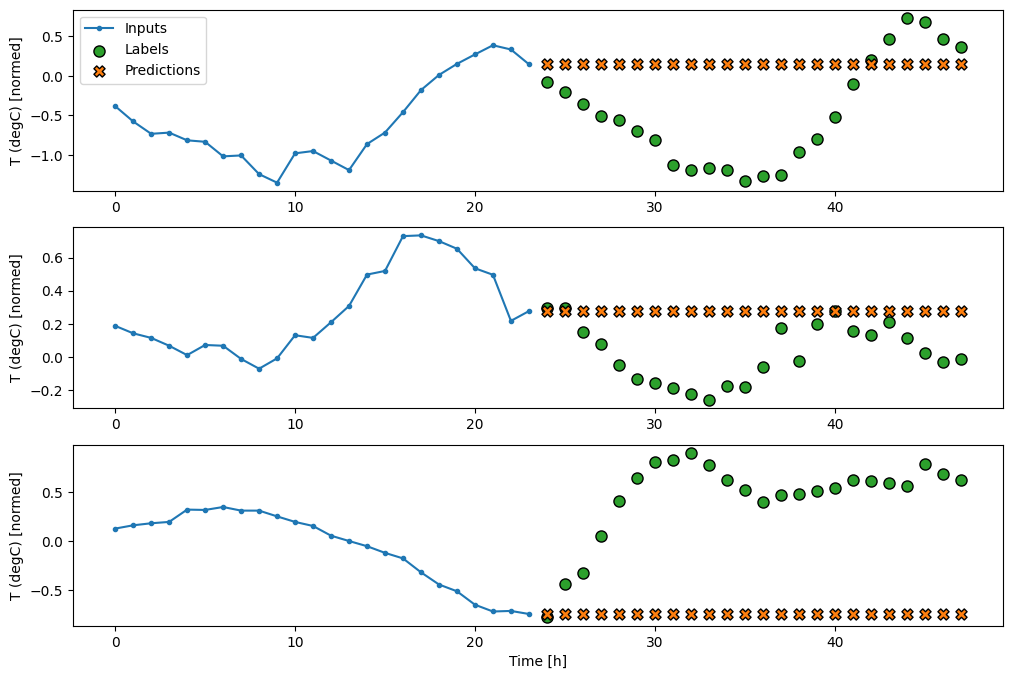
Dado que esta tarea es predecir 24 horas en el futuro, dadas las 24 horas del pasado, otro enfoque simple es repetir el día anterior, asumiendo que mañana será similar:
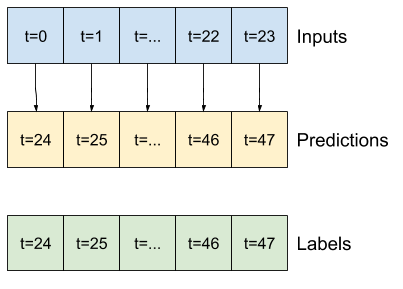
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
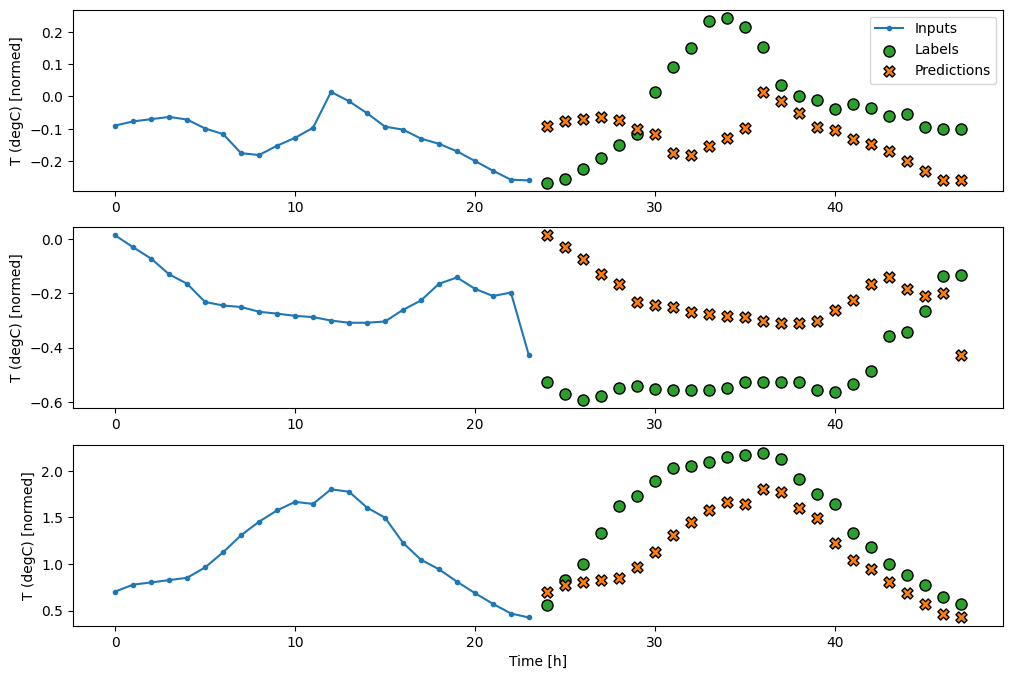
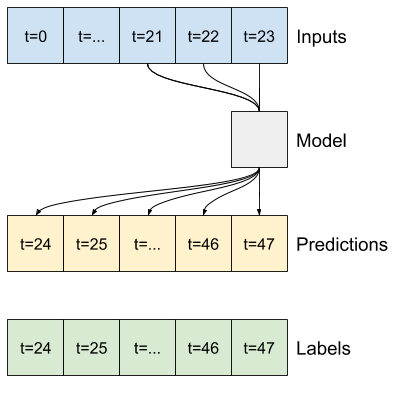
Modelos de disparo único
Un enfoque de alto nivel para este problema es usar un modelo de "disparo único", donde el modelo realiza la predicción de secuencia completa en un solo paso.
Esto se puede implementar de manera eficiente como unidades de salida tf.keras.layers.Dense con OUT_STEPS*features . El modelo solo necesita remodelar esa salida según lo requerido (OUTPUT_STEPS, features) .
Lineal
Un modelo lineal simple basado en el último paso de tiempo de entrada funciona mejor que cualquiera de las líneas base, pero tiene poca potencia. El modelo necesita predecir pasos de tiempo de OUTPUT_STEPS , a partir de un solo paso de tiempo de entrada con una proyección lineal. Solo puede capturar una porción de baja dimensión del comportamiento, probablemente basada principalmente en la hora del día y la época del año.
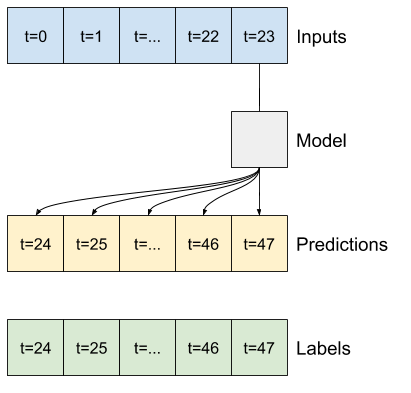
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053
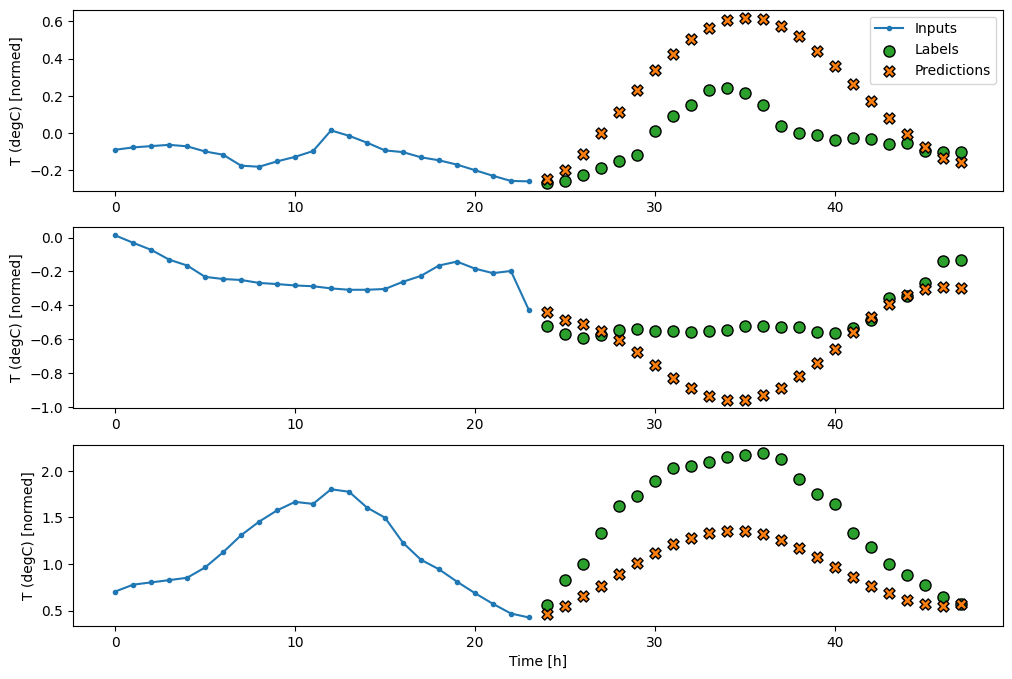
Denso
Agregar un tf.keras.layers.Dense entre la entrada y la salida le da más potencia al modelo lineal, pero aún se basa solo en un solo paso de tiempo de entrada.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
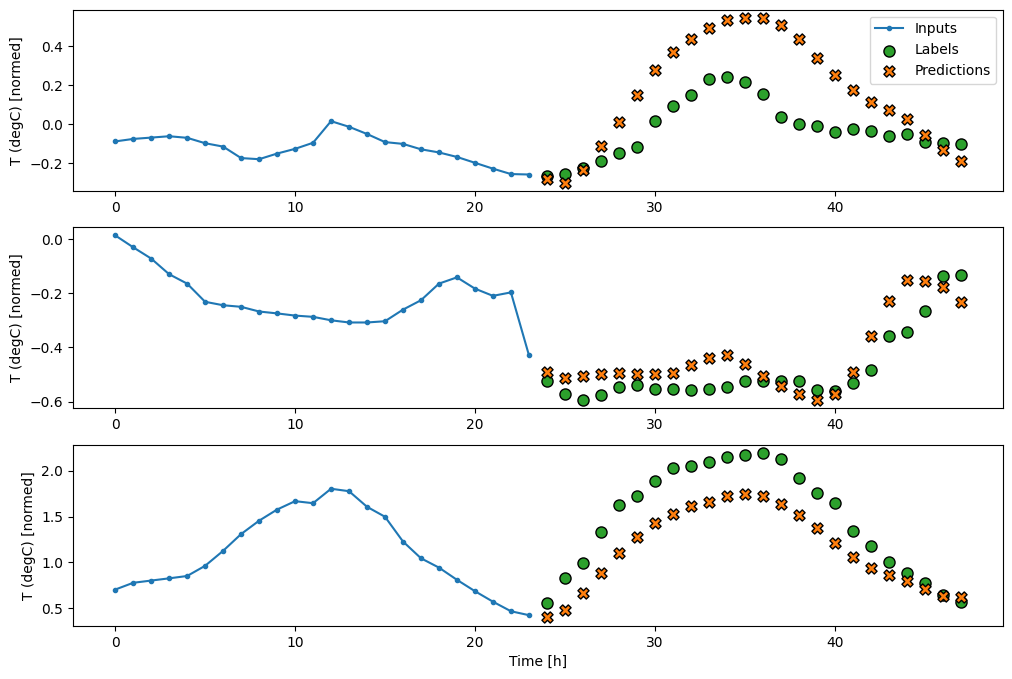
CNN
Un modelo convolucional hace predicciones basadas en un historial de ancho fijo, lo que puede conducir a un mejor rendimiento que el modelo denso, ya que puede ver cómo cambian las cosas con el tiempo:
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
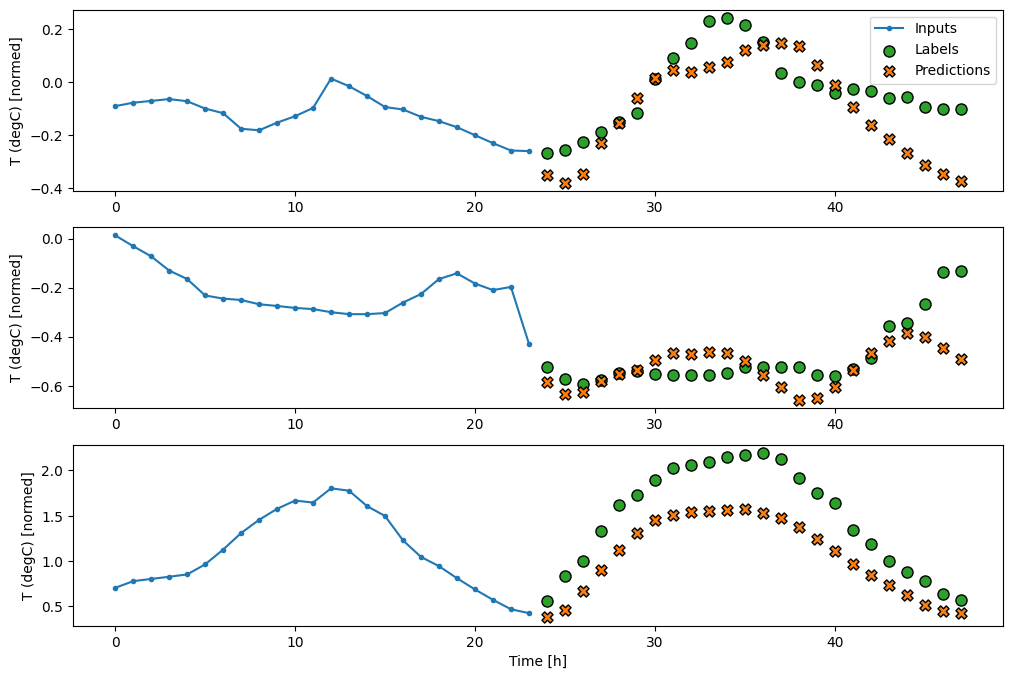
RNN
Un modelo recurrente puede aprender a usar un largo historial de entradas, si es relevante para las predicciones que hace el modelo. Aquí el modelo acumulará el estado interno durante 24 horas, antes de hacer una sola predicción para las próximas 24 horas.
En este formato de disparo único, el LSTM solo necesita producir una salida en el último paso de tiempo, por lo tanto, establezca return_sequences=False en tf.keras.layers.LSTM .
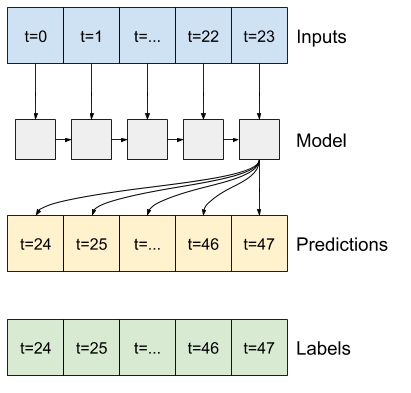
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
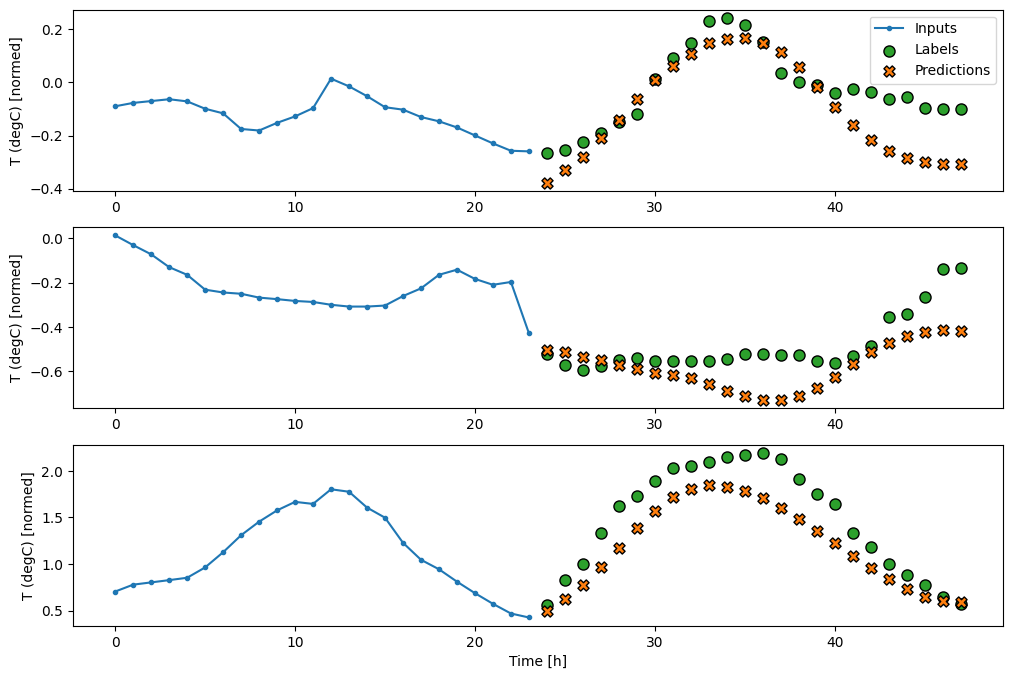
Avanzado: modelo autorregresivo
Todos los modelos anteriores predicen la secuencia de salida completa en un solo paso.
En algunos casos, puede ser útil para el modelo descomponer esta predicción en pasos de tiempo individuales. Luego, la salida de cada modelo se puede retroalimentar en cada paso y se pueden hacer predicciones condicionadas a la anterior, como en el clásico Generating Sequences With Recurrent Neural Networks .
Una clara ventaja de este estilo de modelo es que se puede configurar para producir resultados con una longitud variable.
Puede tomar cualquiera de los modelos de salida múltiple de un solo paso entrenados en la primera mitad de este tutorial y ejecutarlo en un ciclo de retroalimentación autorregresivo, pero aquí se concentrará en crear un modelo que haya sido entrenado explícitamente para hacer eso.
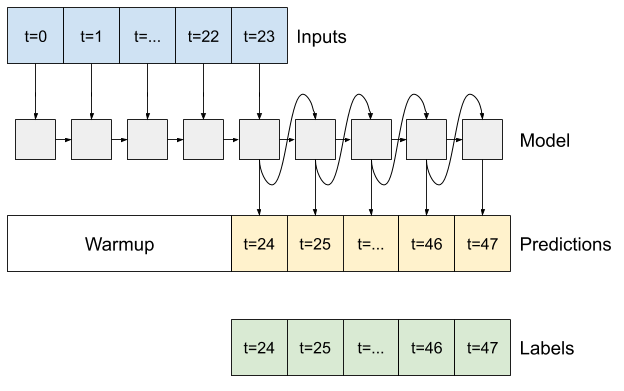
RNN
Este tutorial solo crea un modelo RNN autorregresivo, pero este patrón podría aplicarse a cualquier modelo que se haya diseñado para generar un solo paso de tiempo.
El modelo tendrá la misma forma básica que los modelos LSTM de un solo paso anteriores: una capa tf.keras.layers.LSTM seguida de una capa tf.keras.layers.Dense que convierte los resultados de la capa LSTM en predicciones del modelo.
Un tf.keras.layers.LSTM es un tf.keras.layers.LSTMCell envuelto en el nivel superior tf.keras.layers.RNN que administra el estado y los resultados de la secuencia por usted (Consulte las redes neuronales recurrentes (RNN) con Keras guía para más detalles).
En este caso, el modelo tiene que administrar manualmente las entradas para cada paso, por lo que usa tf.keras.layers.LSTMCell directamente para la interfaz de paso de tiempo único de nivel inferior.
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
El primer método que necesita este modelo es un método de warmup para inicializar su estado interno en función de las entradas. Una vez entrenado, este estado capturará las partes relevantes del historial de entrada. Esto es equivalente al modelo LSTM de un solo paso anterior:
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
Este método devuelve una predicción de un solo paso de tiempo y el estado interno del LSTM :
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
Con el estado de RNN y una predicción inicial, ahora puede continuar iterando el modelo alimentando las predicciones en cada paso hacia atrás como entrada.
El enfoque más simple para recopilar las predicciones de salida es usar una lista de Python y un tf.stack después del bucle.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
Pruebe este modelo en las entradas de ejemplo:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
Ahora, entrena el modelo:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
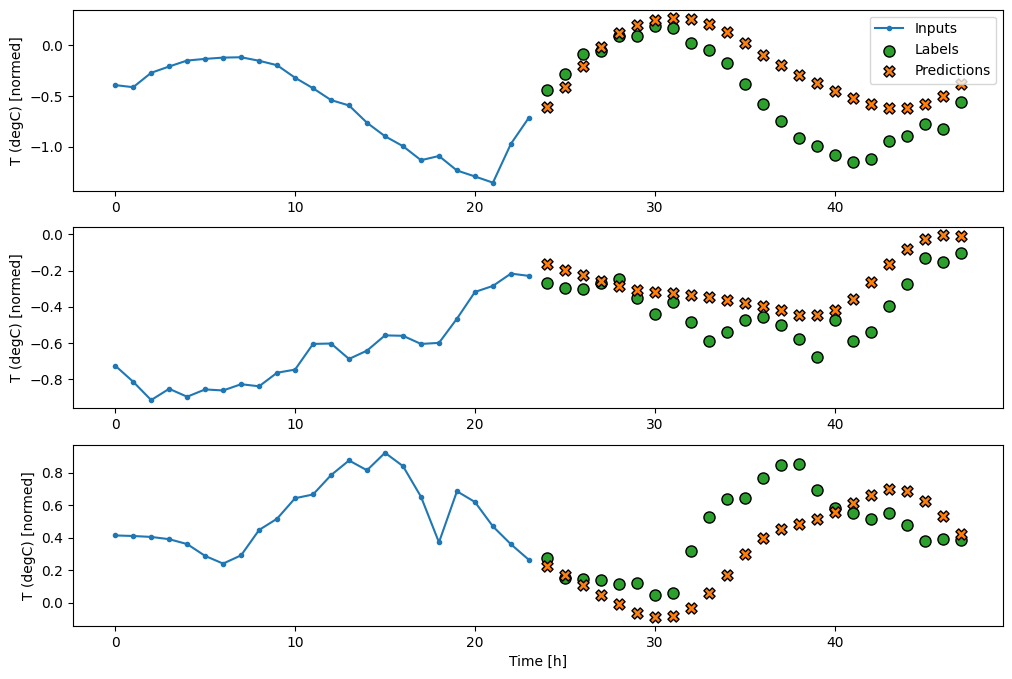
Rendimiento
Hay rendimientos claramente decrecientes en función de la complejidad del modelo en este problema:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()
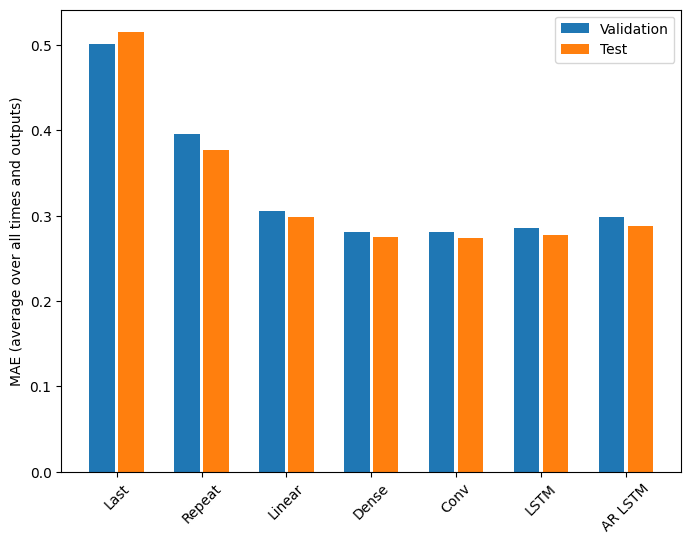
Las métricas para los modelos de salida múltiple en la primera mitad de este tutorial muestran el rendimiento promedio en todas las funciones de salida. Estos rendimientos son similares, pero también se promedian en pasos de tiempo de salida.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
Las ganancias logradas al pasar de un modelo denso a modelos convolucionales y recurrentes son solo un pequeño porcentaje (si es que hay alguno), y el modelo autorregresivo funcionó claramente peor. Por lo tanto, estos enfoques más complejos pueden no valer la pena en este problema, pero no había forma de saberlo sin intentarlo, y estos modelos podrían ser útiles para su problema.
Próximos pasos
Este tutorial fue una introducción rápida a la previsión de series temporales con TensorFlow.
Para obtener más información, consulte:
- Capítulo 15 de Aprendizaje automático práctico con Scikit-Learn, Keras y TensorFlow , 2.ª edición.
- Capítulo 6 de Deep Learning con Python .
- Lección 8 de la introducción de Udacity a TensorFlow para el aprendizaje profundo , incluidos los cuadernos de ejercicios .
Además, recuerda que puedes implementar cualquier modelo de serie de tiempo clásico en TensorFlow; este tutorial solo se enfoca en la funcionalidad integrada de TensorFlow.
