 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Ten samouczek jest wprowadzeniem do prognozowania szeregów czasowych przy użyciu TensorFlow. Buduje kilka różnych stylów modeli, w tym splotowe i rekurencyjne sieci neuronowe (CNN i RNN).
Zostało to omówione w dwóch głównych częściach, z podpunktami:
- Prognoza dla pojedynczego kroku czasowego:
- Pojedyncza funkcja.
- Wszystkie funkcje.
- Prognozuj wiele kroków:
- Pojedynczy strzał: wykonuj wszystkie prognozy naraz.
- Autoregresja: wykonaj jedną prognozę na raz i przekaż dane wyjściowe z powrotem do modelu.
Ustawiać
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
Zbiór danych o pogodzie
W tym samouczku wykorzystano zestaw danych szeregów czasowych dotyczących pogody zarejestrowany przez Instytut Biogeochemii im. Maxa Plancka .
Ten zestaw danych zawiera 14 różnych funkcji, takich jak temperatura powietrza, ciśnienie atmosferyczne i wilgotność. Były one zbierane co 10 minut, począwszy od 2003 roku. W celu zwiększenia wydajności użyjesz tylko danych zebranych w latach 2009-2016. Ta część zbioru danych została przygotowana przez François Chollet do jego książki Deep Learning with Python .
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
Ten samouczek zajmie się tylko prognozami godzinowymi , więc zacznij od podpróbkowania danych z interwałów 10-minutowych do interwałów godzinnych:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
Rzućmy okiem na dane. Oto kilka pierwszych wierszy:
df.head()
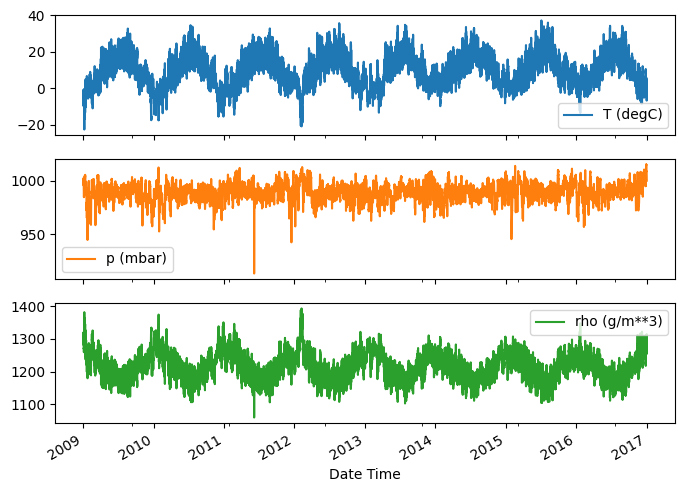
Oto ewolucja kilku funkcji w czasie:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
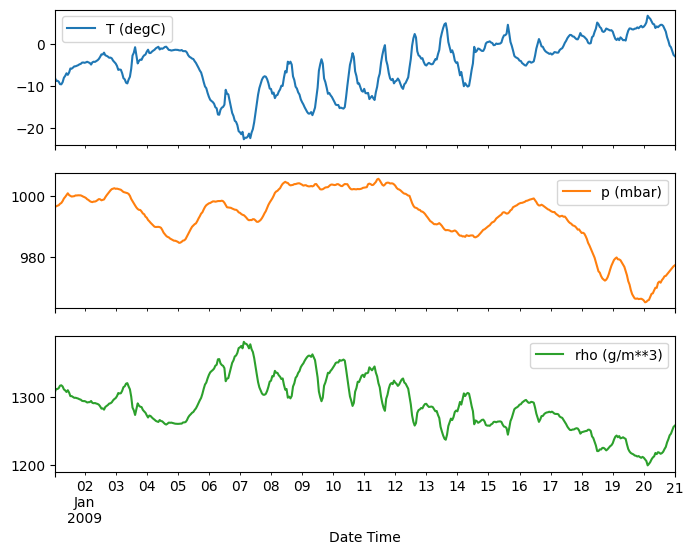
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
Sprawdź i posprzątaj
Następnie spójrz na statystyki zbioru danych:
df.describe().transpose()
Prędkość wiatru
Jedną rzeczą, która powinna się wyróżniać, jest min wartość prędkości wiatru ( wv (m/s) ) i maksymalna ( max. wv (m/s) ). To -9999 jest prawdopodobnie błędne.
Istnieje osobna kolumna kierunku wiatru, więc prędkość powinna być większa od zera ( >=0 ). Zastąp to zerami:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
Inżynieria funkcji
Przed przystąpieniem do budowania modelu ważne jest, aby zrozumieć swoje dane i upewnić się, że przekazujesz odpowiednio sformatowane dane modelu.
Wiatr
Ostatnia kolumna danych, wd (deg) — podaje kierunek wiatru w stopniach. Kąty nie dają dobrych danych wejściowych modelu: 360 ° i 0 ° powinny być blisko siebie i płynnie owijać się wokół. Kierunek nie powinien mieć znaczenia, jeśli wiatr nie wieje.
W tej chwili rozkład danych wiatrowych wygląda tak:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
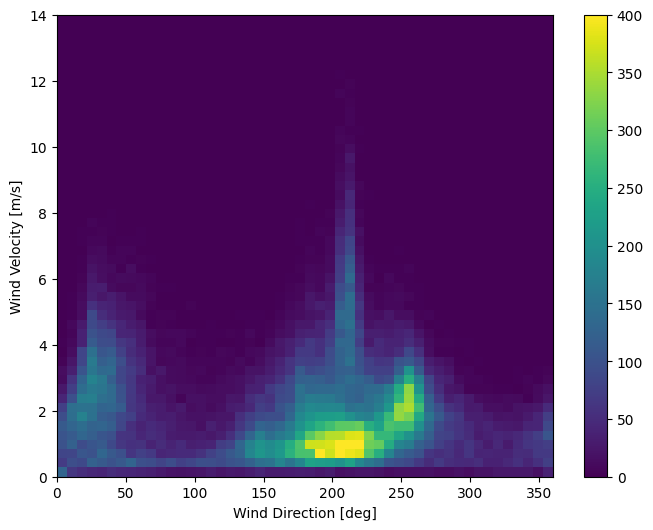
Ale będzie to łatwiejsze do zinterpretowania przez model, jeśli przekształcisz kolumny kierunku i prędkości wiatru na wektor wiatru:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
Rozkład wektorów wiatru jest znacznie prostszy, aby model poprawnie zinterpretował:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)

Czas
Podobnie kolumna Date Time jest bardzo przydatna, ale nie w tej postaci ciągu. Zacznij od konwersji na sekundy:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
Podobnie jak w przypadku kierunku wiatru, czas w sekundach nie jest użytecznym parametrem modelu. Jako dane pogodowe, ma wyraźną dzienną i roczną okresowość. Istnieje wiele sposobów radzenia sobie z okresowością.
Możesz uzyskać użyteczne sygnały, używając przekształceń sinus i cosinus, aby wyczyścić sygnały „Pora dnia” i „Pora roku”:
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
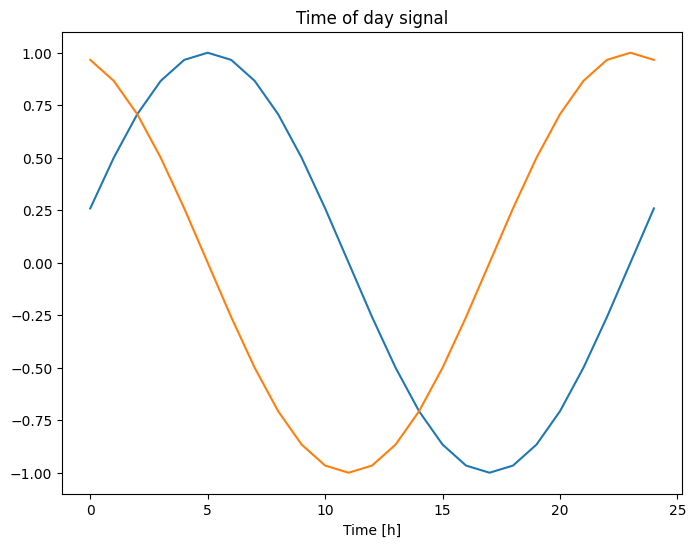
Daje to modelowi dostęp do najważniejszych cech częstotliwości. W tym przypadku wiedziałeś z wyprzedzeniem, które częstotliwości są ważne.
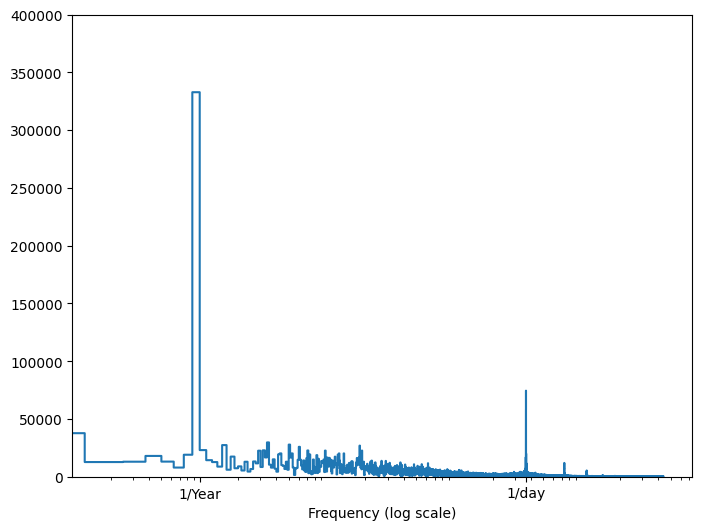
Jeśli nie masz tych informacji, możesz określić, które częstotliwości są ważne, wyodrębniając cechy za pomocą szybkiej transformacji Fouriera . Aby sprawdzić założenia, oto tf.signal.rfft temperatury w czasie. Zwróć uwagę na oczywiste szczyty przy częstotliwościach zbliżonych do 1/year i 1/day :
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
Podziel dane
Użyjesz podziału (70%, 20%, 10%) dla zestawów treningowych, walidacyjnych i testowych. Pamiętaj, że dane nie są losowo tasowane przed podziałem. Dzieje się tak z dwóch powodów:
- Gwarantuje to, że nadal możliwe jest dzielenie danych na okna kolejnych próbek.
- Zapewnia to, że wyniki walidacji/testów są bardziej realistyczne, oceniane na danych zebranych po przeszkoleniu modelu.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
Normalizuj dane
Ważne jest, aby skalować funkcje przed uczeniem sieci neuronowej. Normalizacja jest powszechnym sposobem wykonywania tego skalowania: odejmij średnią i podziel przez odchylenie standardowe każdej cechy.
Średnia i odchylenie standardowe powinny być obliczane tylko przy użyciu danych uczących, aby modele nie miały dostępu do wartości w zbiorach walidacji i testach.
Można również argumentować, że model nie powinien mieć dostępu do przyszłych wartości w zestawie treningowym podczas trenowania i że ta normalizacja powinna być wykonywana przy użyciu średnich kroczących. To nie jest główny temat tego samouczka, a zestawy walidacji i testów zapewniają, że otrzymasz (w pewnym stopniu) uczciwe metryki. Tak więc, w trosce o prostotę, ten samouczek używa prostej średniej.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
Teraz spójrz na rozkład funkcji. Niektóre funkcje mają długie ogony, ale nie ma oczywistych błędów, takich jak wartość prędkości wiatru -9999 .
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

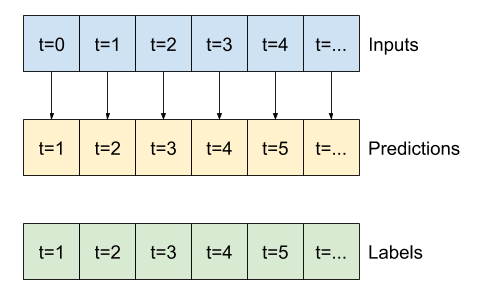
Okno danych
Modele w tym samouczku utworzą zestaw predykcji na podstawie okna kolejnych próbek z danych.
Główne cechy okien wprowadzania to:
- Szerokość (liczba kroków czasowych) okien wprowadzania i etykiet.
- Przesunięcie czasowe między nimi.
- Które funkcje są używane jako dane wejściowe, etykiety lub jedno i drugie.
Ten samouczek buduje różne modele (w tym modele Linear, DNN, CNN i RNN) i używa ich w obu przypadkach:
- Prognozy jednowyjściowe i wielowyjściowe .
- Prognozy jednoetapowe i wieloetapowe .
Ta sekcja koncentruje się na implementacji okienkowania danych, aby można je było ponownie wykorzystać we wszystkich tych modelach.
W zależności od zadania i typu modelu możesz chcieć wygenerować różne okna danych. Oto kilka przykładów:
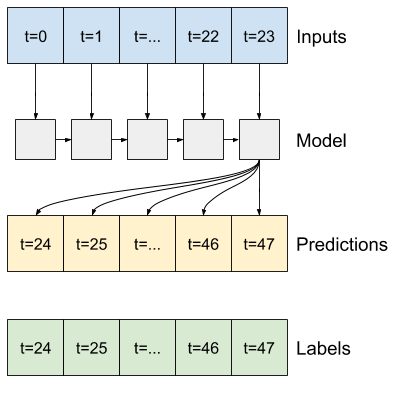
Na przykład, aby dokonać pojedynczej prognozy na 24 godziny w przyszłość, biorąc pod uwagę 24 godziny historii, możesz zdefiniować okno w następujący sposób:
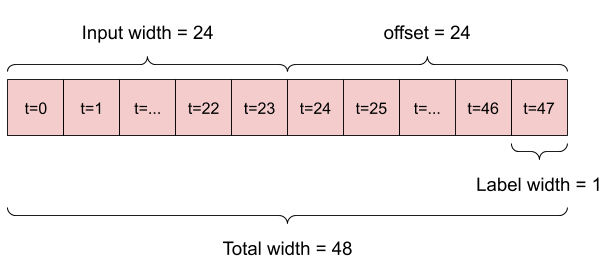
Model, który dokonuje prognozy na godzinę w przyszłość, biorąc pod uwagę sześć godzin historii, potrzebowałby takiego okna:

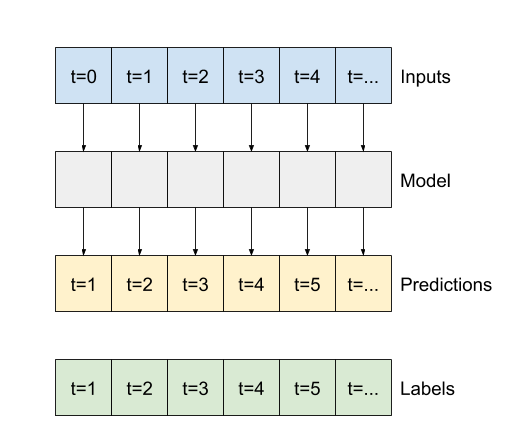
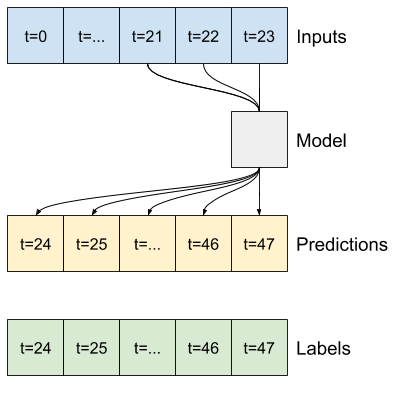
Pozostała część tej sekcji definiuje klasę WindowGenerator . Ta klasa może:
- Postępuj z indeksami i przesunięciami, jak pokazano na powyższych schematach.
- Podziel okna funkcji na pary
(features, labels). - Wykreśl zawartość wynikowych okien.
- Wydajnie generuj partie tych okien na podstawie danych uczących, oceniających i testowych przy użyciu
tf.data.Datasets.
1. Indeksy i przesunięcia
Zacznij od utworzenia klasy WindowGenerator . Metoda __init__ zawiera całą niezbędną logikę dla indeksów wejściowych i etykiet.
Jako dane wejściowe pobiera również szkolenie, ocenę i testowanie ramek DataFrames. Zostaną one później przekonwertowane na tf.data.Dataset systemu Windows.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
Oto kod do tworzenia 2 okien pokazanych na diagramach na początku tej sekcji:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. Podział
Mając listę kolejnych danych wejściowych, metoda split_window przekonwertuje je na okno danych wejściowych i okno etykiet.
Zdefiniowany wcześniej przykład w2 zostanie podzielony w ten sposób:
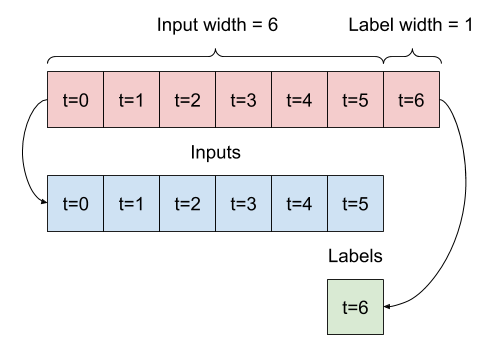
Ten diagram nie przedstawia osi features danych, ale ta funkcja split_window obsługuje również label_columns , dzięki czemu można jej używać zarówno w przykładach z pojedynczym wyjściem, jak i z wieloma wyjściami.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
Wypróbuj to:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
Zazwyczaj dane w TensorFlow są pakowane w tablice, w których najbardziej zewnętrzny indeks znajduje się w przykładach (wymiar „partia”). Środkowe indeksy to wymiar(y) „czasu” lub „przestrzeni” (szerokość, wysokość). Najbardziej wewnętrznymi indeksami są cechy.
Powyższy kod wziął partię trzech okien z 7-krokami czasowymi z 19 funkcjami w każdym kroku czasowym. Dzieli je na partię 6-krotnych wejść 19-funkcyjnych i 1-krotną etykietę 1-funkcyjną. Etykieta ma tylko jedną funkcję, ponieważ WindowGenerator został zainicjowany za pomocą label_columns=['T (degC)'] . Początkowo w tym samouczku zbuduje się modele, które przewidują pojedyncze etykiety wyjściowe.
3. Działka
Oto metoda kreślenia, która pozwala na prostą wizualizację podzielonego okna:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
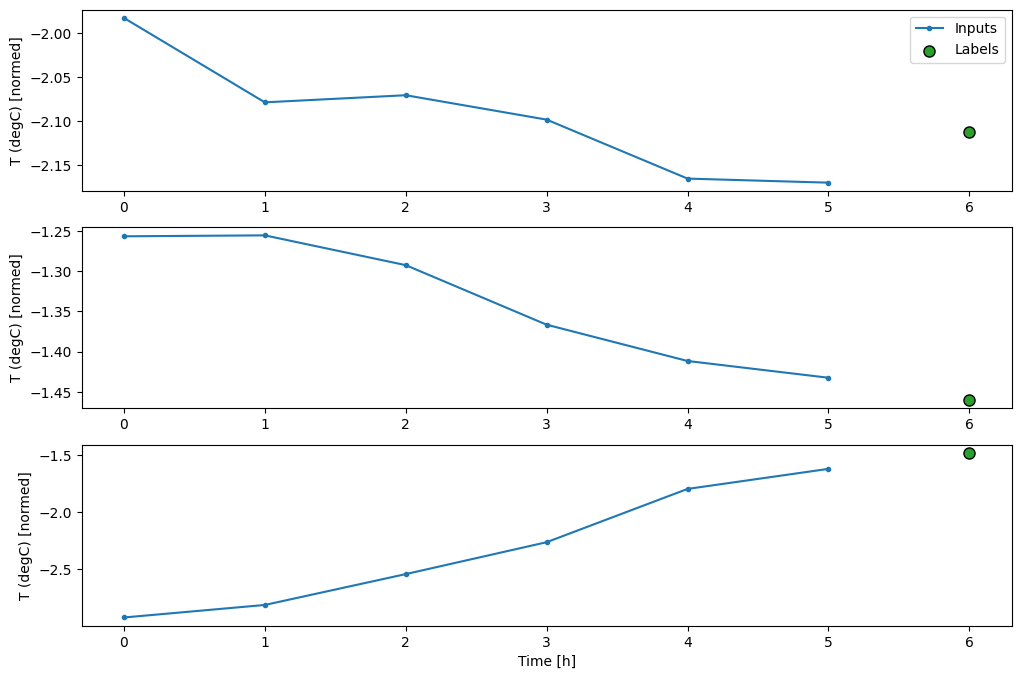
Ten wykres wyrównuje dane wejściowe, etykiety i (później) prognozy na podstawie czasu, do którego odnosi się element:
w2.plot()
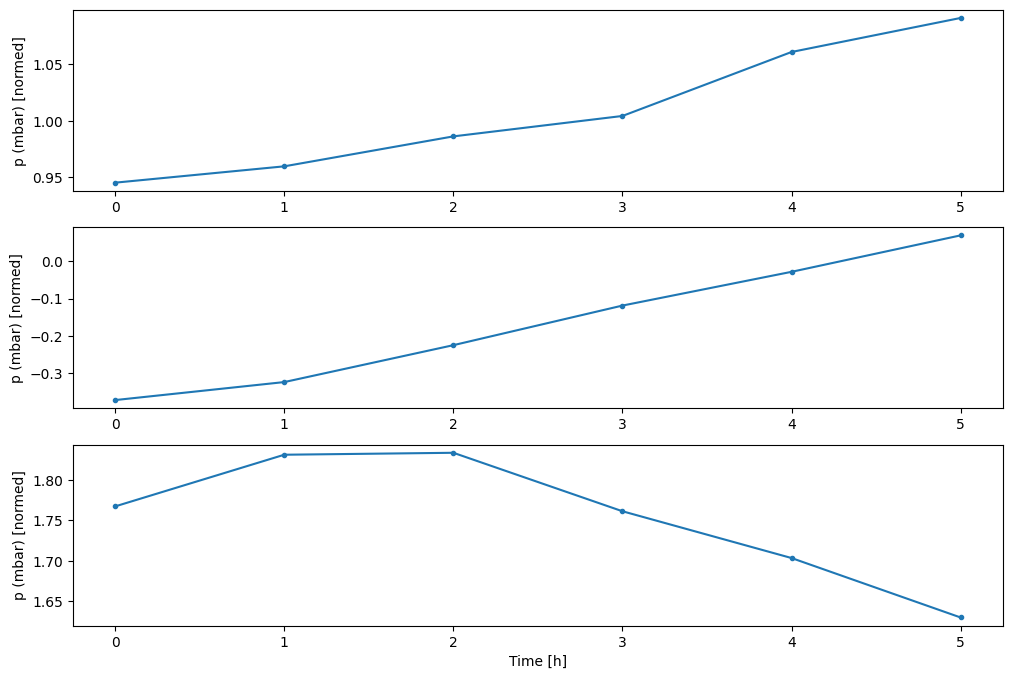
Możesz wykreślić inne kolumny, ale przykładowa konfiguracja okna w2 ma tylko etykiety dla kolumny T (degC) .
w2.plot(plot_col='p (mbar)')
4. Utwórz tf.data.Dataset s
Na koniec ta metoda make_dataset pobierze DataFrame szeregu czasowego i przekonwertuje go na zestaw tf.data.Dataset się z par (input_window, label_window) przy użyciu funkcji tf.keras.utils.timeseries_dataset_from_array :
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
Obiekt WindowGenerator zawiera dane szkoleniowe, walidacyjne i testowe.
Dodaj właściwości umożliwiające dostęp do nich jako tf.data.Dataset s przy użyciu zdefiniowanej wcześniej metody make_dataset . Dodaj również standardową przykładową wiązkę, aby uzyskać łatwy dostęp i kreślić:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
Teraz obiekt WindowGenerator zapewnia dostęp do obiektów tf.data.Dataset , dzięki czemu można łatwo iterować dane.
Właściwość Dataset.element_spec informuje o strukturze, typach danych i kształtach elementów zestawu danych.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
Iteracja po zbiorze Dataset daje konkretne partie:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
Modele jednoetapowe
Najprostszy model, jaki można zbudować na tego rodzaju danych, to taki, który przewiduje wartość pojedynczej funkcji — 1 krok czasowy (jedna godzina) w przyszłość na podstawie tylko bieżących warunków.
Zacznij więc od budowania modeli do przewidywania wartości T (degC) na godzinę w przyszłość.
Skonfiguruj obiekt WindowGenerator , aby generował następujące pary jednoetapowe (input, label) :
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
Obiekt window tworzy tf.data.Dataset z zestawów uczących, walidacyjnych i testowych, co pozwala na łatwe iterowanie po partiach danych.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
Linia bazowa
Przed zbudowaniem trenowalnego modelu dobrze byłoby mieć podstawę wydajności jako punkt do porównania z późniejszymi, bardziej skomplikowanymi modelami.
Pierwszym zadaniem jest przewidzenie temperatury na godzinę w przyszłość, biorąc pod uwagę aktualną wartość wszystkich funkcji. Aktualne wartości zawierają aktualną temperaturę.
Zacznij więc od modelu, który po prostu zwraca bieżącą temperaturę jako przewidywanie, przewidując „Brak zmian”. Jest to rozsądna linia bazowa, ponieważ temperatura zmienia się powoli. Oczywiście ta podstawa będzie działać gorzej, jeśli dokonasz prognozy w przyszłości.
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
Utwórz wystąpienie i oceń ten model:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
To wydrukowało pewne wskaźniki wydajności, ale nie dają one wyczucia, jak dobrze radzi sobie model.
WindowGenerator ma metodę kreślenia, ale wykresy nie będą zbyt interesujące z tylko jedną próbką.
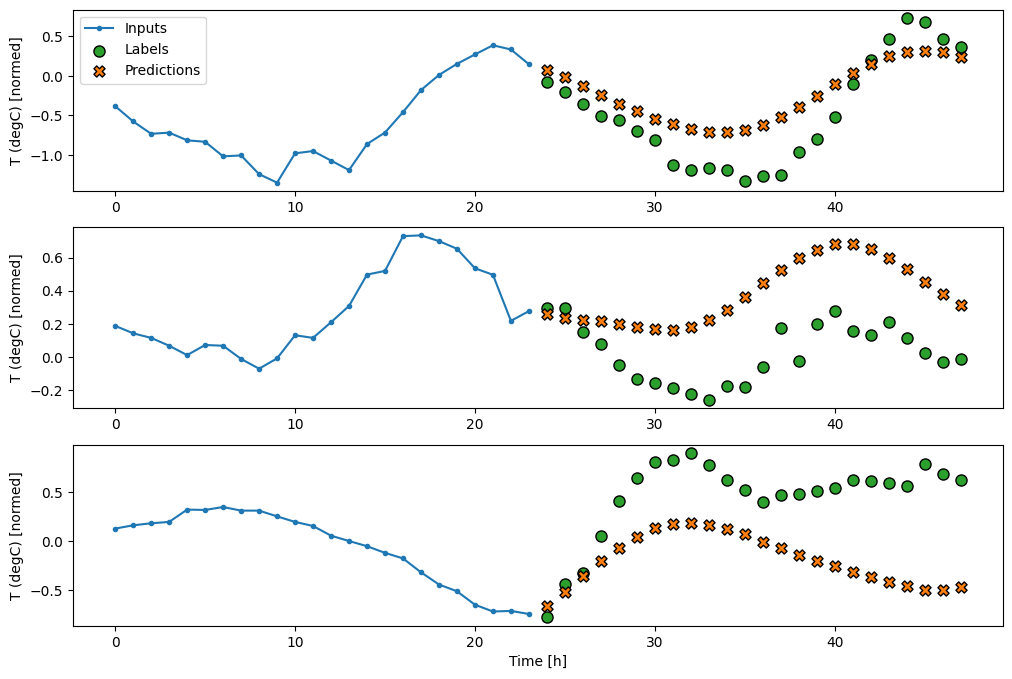
Stwórz więc szerszy WindowGenerator , który generuje okna 24 godziny kolejnych danych wejściowych i etykiet na raz. Nowa zmienna wide_window nie zmienia sposobu działania modelu. Model nadal tworzy prognozy o godzinę w przyszłość na podstawie pojedynczego wejściowego kroku czasowego. Tutaj oś time działa jak oś batch : każda prognoza jest wykonywana niezależnie, bez interakcji między krokami czasu:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
To rozwinięte okno można przekazać bezpośrednio do tego samego modelu baseline bez żadnych zmian w kodzie. Jest to możliwe, ponieważ dane wejściowe i etykiety mają tę samą liczbę przedziałów czasowych, a linia bazowa po prostu przekazuje dane wejściowe do danych wyjściowych:
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
Wykreślając prognozy modelu bazowego, zauważ, że są to po prostu etykiety przesunięte w prawo o godzinę:
wide_window.plot(baseline)
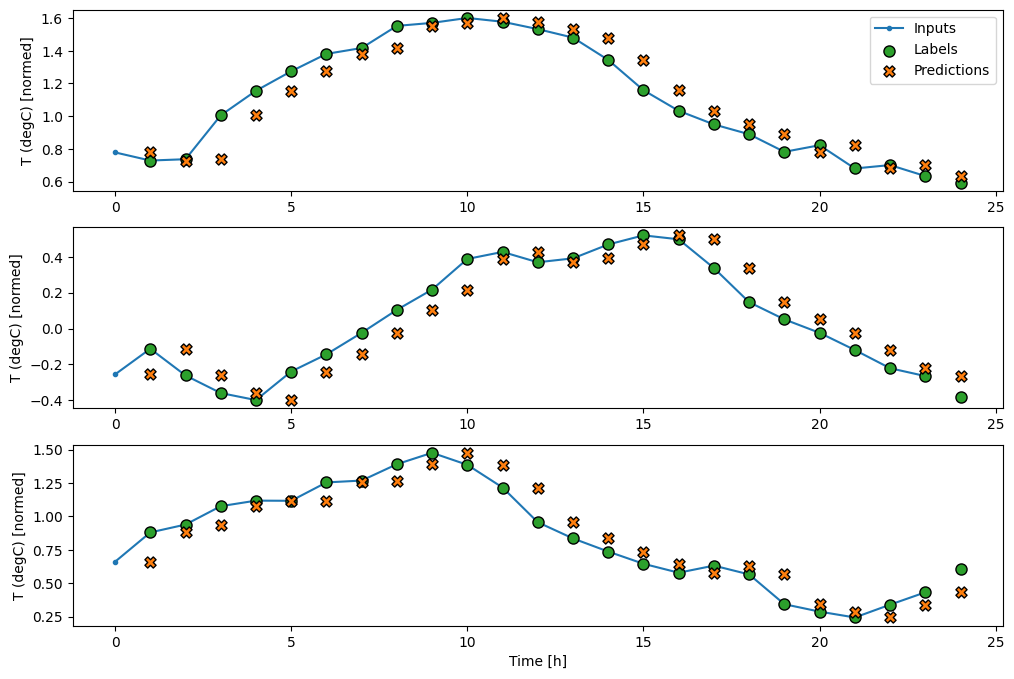
Na powyższych wykresach trzech przykładów model jednoetapowy prowadzony jest w ciągu 24 godzin. To zasługuje na wyjaśnienie:
- Niebieska linia
Inputspokazuje temperaturę wejściową w każdym kroku czasowym. Model otrzymuje wszystkie cechy, ten wykres pokazuje tylko temperaturę. - Zielone kropki
Labelspokazują docelową wartość przewidywania. Te kropki są wyświetlane w czasie przewidywania, a nie w czasie wprowadzania. Dlatego zakres etykiet jest przesunięty o 1 krok względem wejść. - Pomarańczowe krzyżyki
Predictionsto przewidywania modelu dla każdego wyjściowego kroku czasowego. Gdyby model przewidywał doskonale, przewidywania trafiałyby bezpośrednio naLabels.
Model liniowy
Najprostszym modelem, który można wytrenować, jest wstawienie transformacji liniowej między dane wejściowe a dane wyjściowe. W tym przypadku wynik kroku czasowego zależy tylko od tego kroku:

Warstwa tf.keras.layers.Dense bez zestawu activation jest modelem liniowym. Warstwa przekształca tylko ostatnią oś danych z (batch, time, inputs) na (batch, time, units) ; jest stosowany niezależnie do każdego elementu na osiach batch i time .
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
Ten samouczek szkoli wiele modeli, więc spakuj procedurę uczenia w funkcję:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
Wytrenuj model i oceń jego wydajność:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
Podobnie jak model baseline , model liniowy można wywołać w partiach szerokich okien. Używany w ten sposób model tworzy zestaw niezależnych predykcji na kolejnych krokach czasowych. Oś time działa jak inna oś batch . Nie ma interakcji między przewidywaniami na każdym kroku czasowym.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
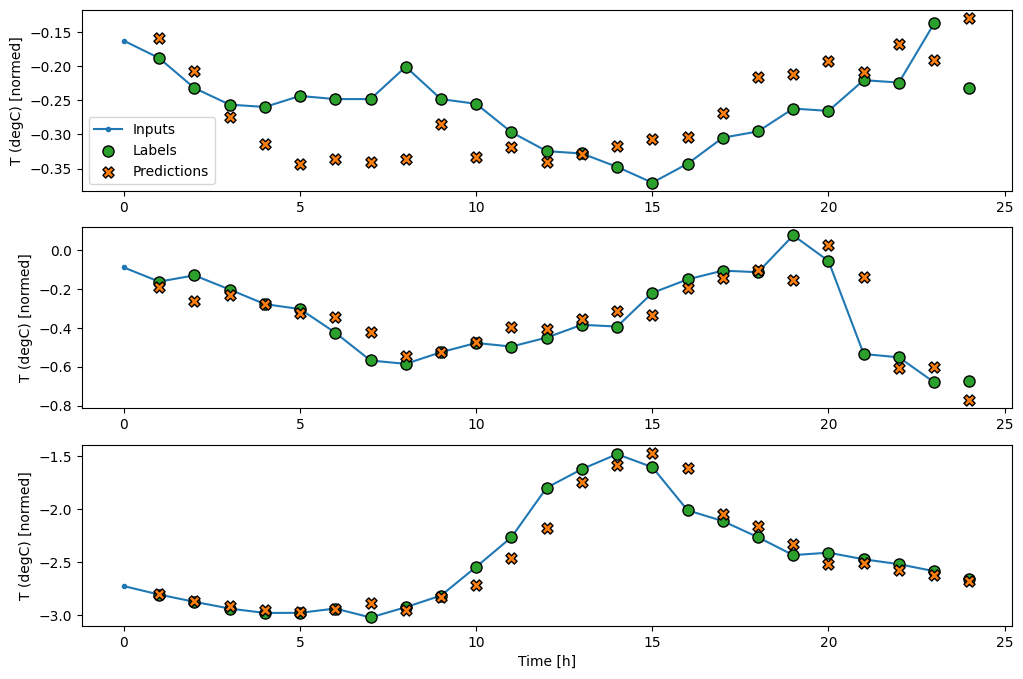
Oto wykres jego przykładowych przewidywań na wide_window , zauważ, jak w wielu przypadkach przewidywanie jest wyraźnie lepsze niż tylko zwracanie temperatury wejściowej, ale w kilku przypadkach jest gorsze:
wide_window.plot(linear)
Jedną z zalet modeli liniowych jest to, że są stosunkowo proste w interpretacji. Możesz wyciągnąć wagi warstwy i zwizualizować wagę przypisaną do każdego wejścia:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
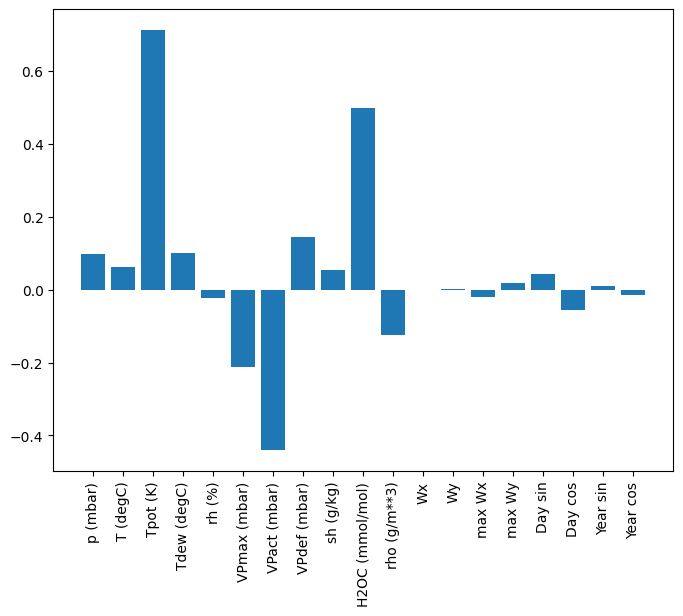
Czasami model nie przykłada nawet największej wagi do wejścia T (degC) . Jest to jedno z zagrożeń związanych z losową inicjalizacją.
Gęsty
Przed zastosowaniem modeli, które faktycznie działają na wielu krokach czasowych, warto sprawdzić wydajność głębszych, bardziej wydajnych modeli z pojedynczym krokiem wejściowym.
Oto model podobny do modelu linear , z wyjątkiem tego, że układa kilka warstw Dense między wejściem a wyjściem:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
Wieloetapowy gęsty
Model z pojedynczym krokiem czasowym nie ma kontekstu dla bieżących wartości jego danych wejściowych. Nie widzi, jak funkcje wejściowe zmieniają się w czasie. Aby rozwiązać ten problem, model potrzebuje dostępu do wielu kroków czasowych podczas tworzenia prognoz:
Modele baseline , linear i dense obsługiwane są niezależnie dla każdego kroku czasowego. W tym przypadku model przyjmie wiele kroków czasowych jako dane wejściowe, aby wytworzyć jedno wyjście.
Utwórz WindowGenerator , który będzie generował partie trzygodzinnych danych wejściowych i jednogodzinnych etykiet:
Zauważ, że parametr shift Window odnosi się do końca dwóch okien.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
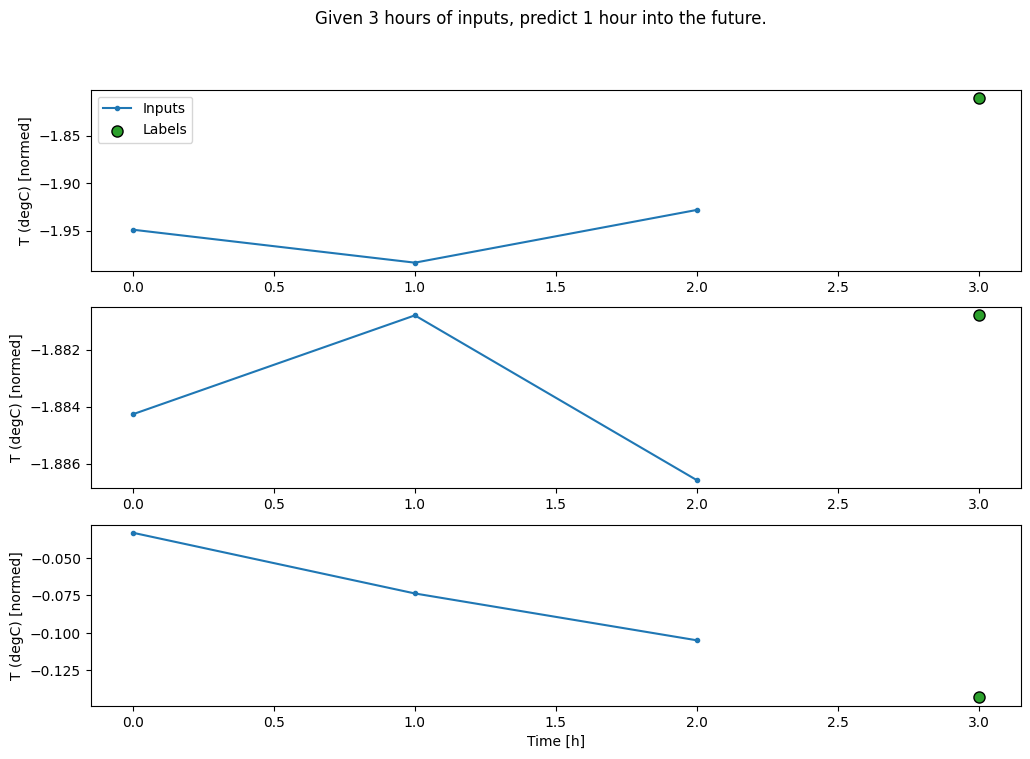
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
Możesz trenować dense model w oknie z wieloma krokami wejściowymi, dodając tf.keras.layers.Flatten jako pierwszą warstwę modelu:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
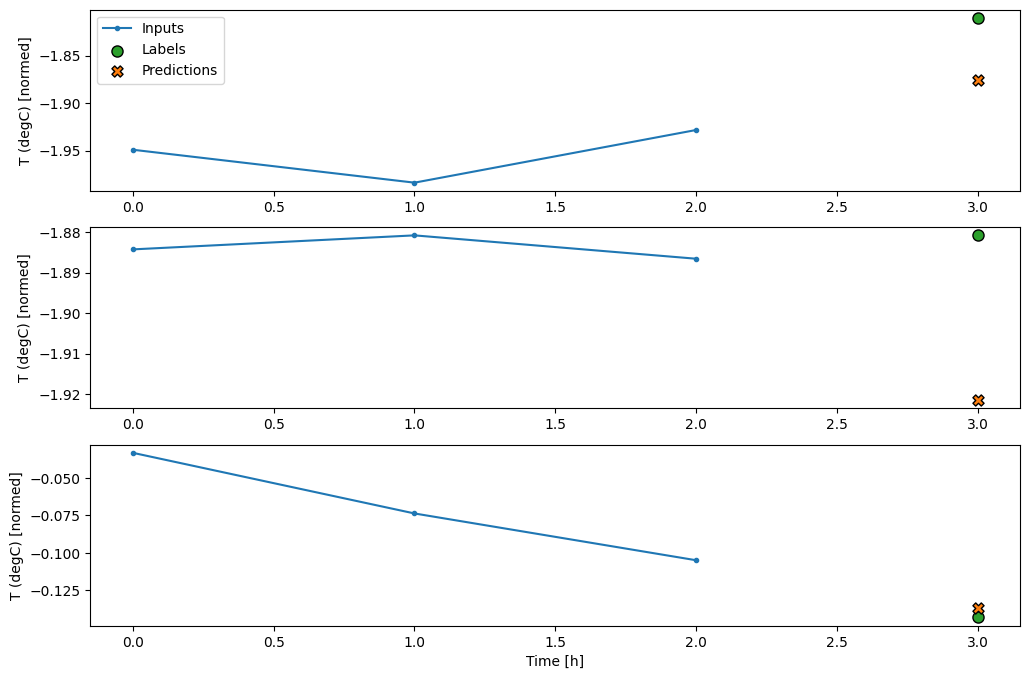
conv_window.plot(multi_step_dense)
Główną wadą tego podejścia jest to, że wynikowy model można wykonać tylko na oknach wejściowych o dokładnie takim kształcie.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
Modele splotowe w następnej sekcji rozwiązują ten problem.
Konwolucyjna sieć neuronowa
Warstwa konwolucji ( tf.keras.layers.Conv1D ) również przyjmuje wiele kroków czasowych jako dane wejściowe do każdej prognozy.
Poniżej znajduje się ten sam model co multi_step_dense , przepisany ze splotem.
Zwróć uwagę na zmiany:
-
tf.keras.layers.Flatteni pierwszytf.keras.layers.Densezostały zastąpione przeztf.keras.layers.Conv1D. -
tf.keras.layers.Reshapenie jest już potrzebny, ponieważ splot utrzymuje oś czasu na wyjściu.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
Uruchom go na przykładowej partii, aby sprawdzić, czy model generuje dane wyjściowe o oczekiwanym kształcie:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
Trenuj i oceniaj go w conv_window i powinien dawać wydajność zbliżoną do modelu multi_step_dense .
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
Różnica między tym conv_model a modelem multi_step_dense polega na tym, że model conv_model może być uruchamiany na danych wejściowych o dowolnej długości. Warstwa splotowa jest nakładana na przesuwane okno danych wejściowych:

Jeśli uruchomisz go na szerszym wejściu, da szersze wyjście:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
Zauważ, że wyjście jest krótsze niż wejście. Aby szkolenie lub kreślenie działało, etykiety i prognozy muszą mieć tę samą długość. Zbuduj więc WindowGenerator , aby generować szerokie okna z kilkoma dodatkowymi krokami czasu wejściowego, tak aby długości etykiety i przewidywania były zgodne:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
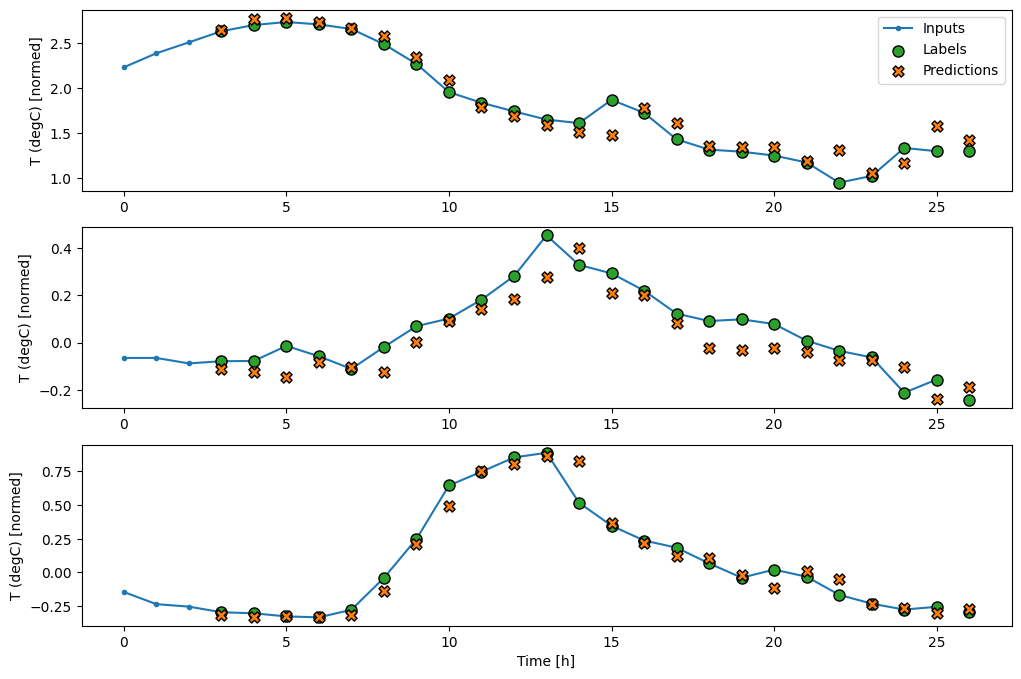
Teraz możesz wykreślić prognozy modelu w szerszym oknie. Zwróć uwagę na 3 kroki czasowe wprowadzania danych przed pierwszą prognozą. Każda prognoza tutaj opiera się na 3 poprzednich krokach czasowych:
wide_conv_window.plot(conv_model)
Sieć neuronowa rekurencyjna
Recurrent Neural Network (RNN) to rodzaj sieci neuronowej dobrze dopasowanej do danych szeregów czasowych. RNN przetwarzają szeregi czasowe krok po kroku, utrzymując stan wewnętrzny od kroku do kroku czasowego.
Więcej informacji można znaleźć w podręczniku Generowanie tekstu z samouczkiem RNN oraz w przewodniku Recurrent Neural Networks (RNN) with Keras .
W tym samouczku użyjesz warstwy RNN o nazwie Long Short-Term Memory ( tf.keras.layers.LSTM ).
Ważnym argumentem konstruktora dla wszystkich warstw Keras RNN, takich jak tf.keras.layers.LSTM , jest argument return_sequences . To ustawienie może skonfigurować warstwę na jeden z dwóch sposobów:
- Jeśli
Falsejest wartością domyślną, warstwa zwraca tylko dane wyjściowe ostatniego kroku czasowego, dając modelowi czas na rozgrzanie swojego stanu wewnętrznego przed wykonaniem pojedynczej prognozy:
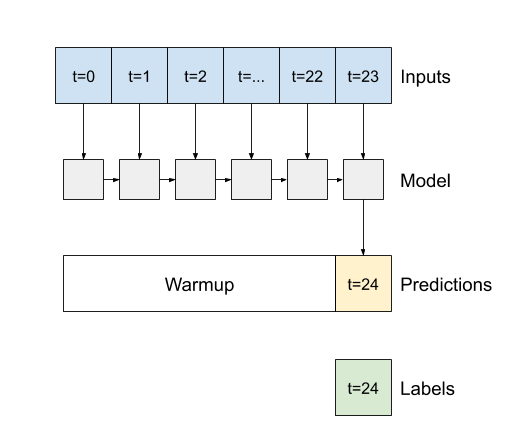
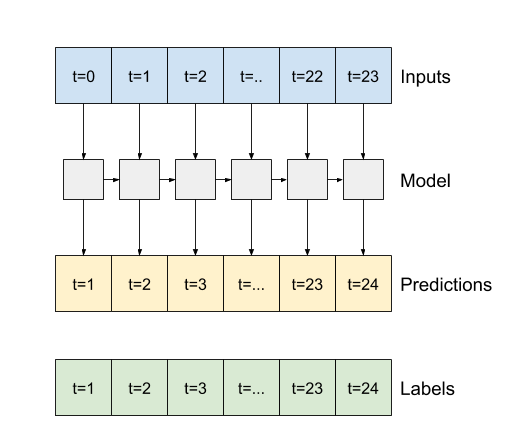
- Jeśli
True, warstwa zwraca dane wyjściowe dla każdego wejścia. Jest to przydatne w przypadku:- Układanie warstw RNN.
- Trening modelu na wielu krokach czasowych jednocześnie.
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
Z return_sequences=True , model może być trenowany na 24 godzinach danych na raz.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
wide_window.plot(lstm_model)
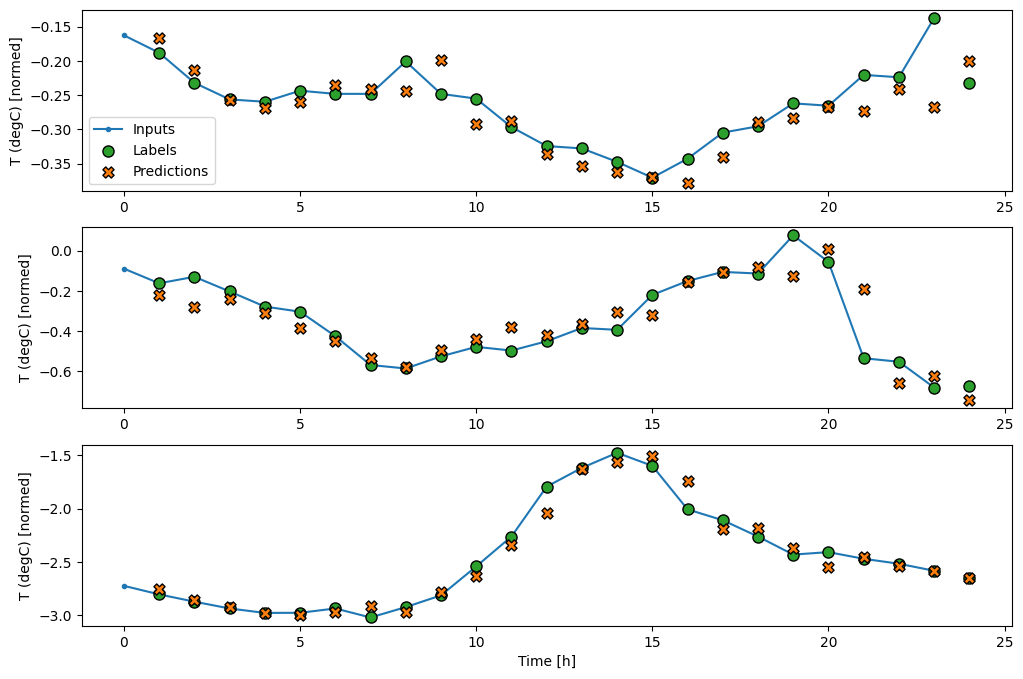
Wydajność
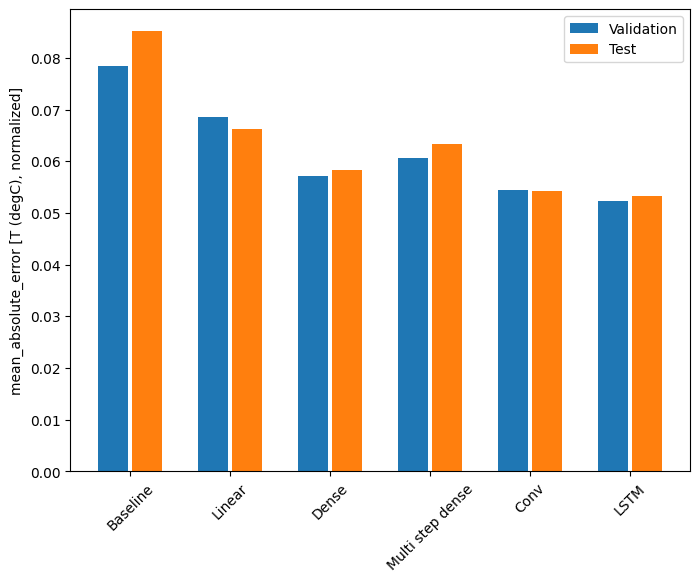
Z tym zestawem danych zazwyczaj każdy z modeli radzi sobie nieco lepiej niż poprzedni:
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()
for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
Modele z wieloma wyjściami
Wszystkie dotychczasowe modele przewidywały pojedynczą cechę wyjściową T (degC) dla pojedynczego kroku czasowego.
Wszystkie te modele można przekonwertować w celu przewidywania wielu funkcji, zmieniając liczbę jednostek w warstwie wyjściowej i dostosowując okna uczenia, aby uwzględnić wszystkie funkcje w labels ( example_labels ):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
Zwróć uwagę, że oś features etykiet ma teraz taką samą głębokość jak dane wejściowe, zamiast 1 .
Linia bazowa
Można tutaj użyć tego samego modelu bazowego ( Baseline ), ale tym razem z powtórzeniem wszystkich funkcji zamiast wybierania określonego label_index :
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
Gęsty
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
RNN
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
Zaawansowane: Pozostałe połączenia
Wcześniejszy model Baseline wykorzystywał fakt, że kolejność nie zmienia się drastycznie z kroku na krok. Każdy model przeszkolony do tej pory w tym samouczku został losowo zainicjowany, a następnie musiał nauczyć się, że dane wyjściowe są małą zmianą w stosunku do poprzedniego kroku czasowego.
Chociaż można obejść ten problem dzięki starannej inicjalizacji, łatwiej jest wbudować to w strukturę modelu.
W analizie szeregów czasowych często buduje się modele, które zamiast przewidywać następną wartość, przewidują zmianę wartości w następnym przedziale czasowym. Podobnie sieci resztkowe — lub ResNets — w uczeniu głębokim odnoszą się do architektur, w których każda warstwa dodaje się do akumulowanego wyniku modelu.
W ten sposób korzystasz ze świadomości, że zmiana powinna być niewielka.
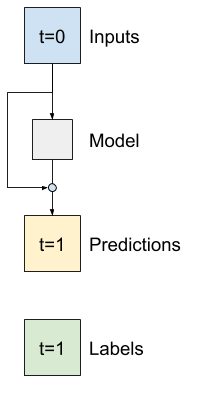
Zasadniczo inicjuje to model tak, aby pasował do Baseline . W tym zadaniu pomaga modelom szybciej się zbiegać, z nieco lepszą wydajnością.
To podejście może być używane w połączeniu z dowolnym modelem omówionym w tym samouczku.
Tutaj jest on stosowany do modelu LSTM, zwróć uwagę na użycie tf.initializers.zeros , aby upewnić się, że początkowe przewidywane zmiany są niewielkie i nie przeciążają pozostałego połączenia. Nie ma tutaj obaw o łamanie symetrii dla gradientów, ponieważ zeros są używane tylko w ostatniej warstwie.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
Wydajność
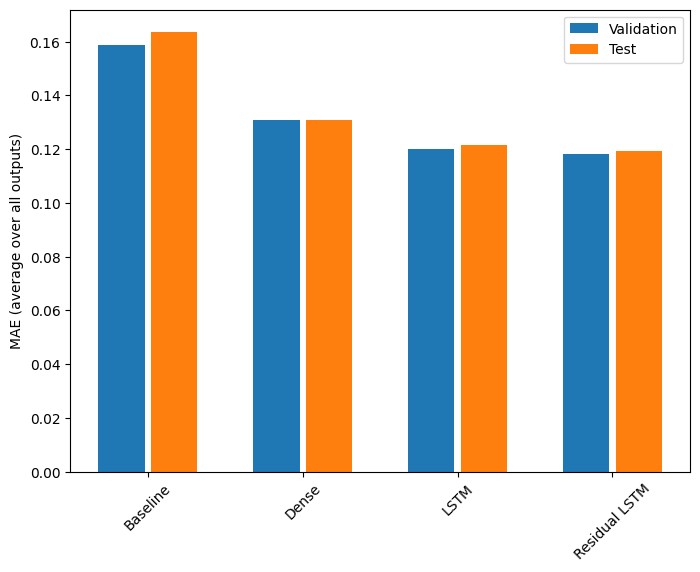
Oto ogólna wydajność tych modeli z wieloma wyjściami.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
Powyższe wyniki są uśredniane dla wszystkich wyników modelu.
Modele wieloetapowe
Zarówno modele jednowyjściowe, jak i wielowyjściowe w poprzednich sekcjach przewidywały jeden krok w czasie , godzinę w przyszłość.
W tej sekcji przyjrzymy się , jak rozszerzyć te modele , aby umożliwić przewidywanie wielu kroków czasowych .
W przewidywaniu wieloetapowym model musi nauczyć się przewidywać zakres przyszłych wartości. W ten sposób, w przeciwieństwie do modelu jednoetapowego, w którym przewidywany jest tylko jeden punkt w przyszłości, model wieloetapowy przewiduje sekwencję przyszłych wartości.
Istnieją dwa przybliżone podejścia do tego:
- Prognozy pojedynczych strzałów, w których cały szereg czasowy jest przewidywany jednocześnie.
- Predykcje autoregresyjne, w których model wykonuje tylko predykcje jednoetapowe, a jego dane wyjściowe są zwracane jako dane wejściowe.
W tej sekcji wszystkie modele będą przewidywać wszystkie cechy we wszystkich wyjściowych przedziałach czasowych .
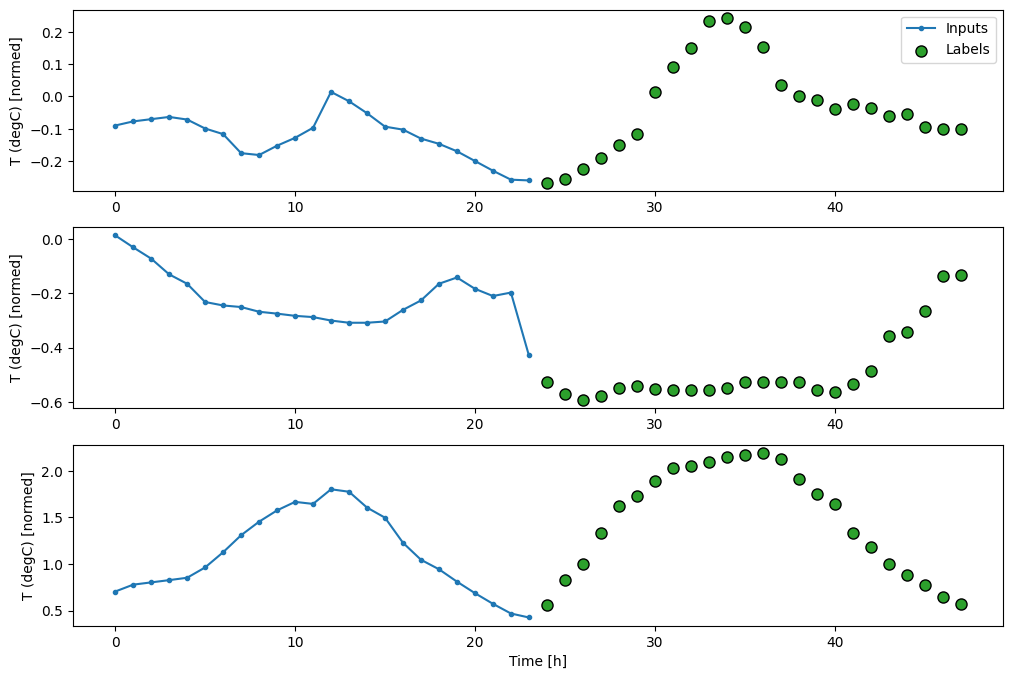
W przypadku modelu wieloetapowego dane szkoleniowe ponownie składają się z próbek godzinowych. Jednak tutaj modele nauczą się przewidywać 24 godziny w przyszłość, biorąc pod uwagę 24 godziny w przeszłości.
Oto obiekt Window , który generuje te wycinki z zestawu danych:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
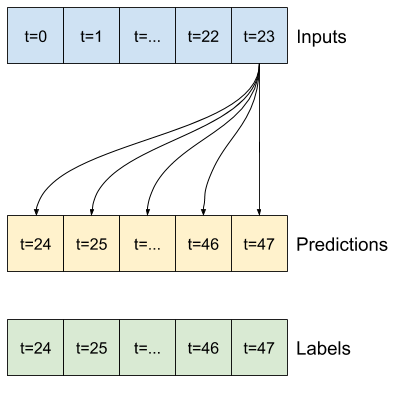
Linie bazowe
Prostym punktem odniesienia dla tego zadania jest powtórzenie ostatniego wejściowego kroku czasowego dla wymaganej liczby wyjściowych kroków czasowych:
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007
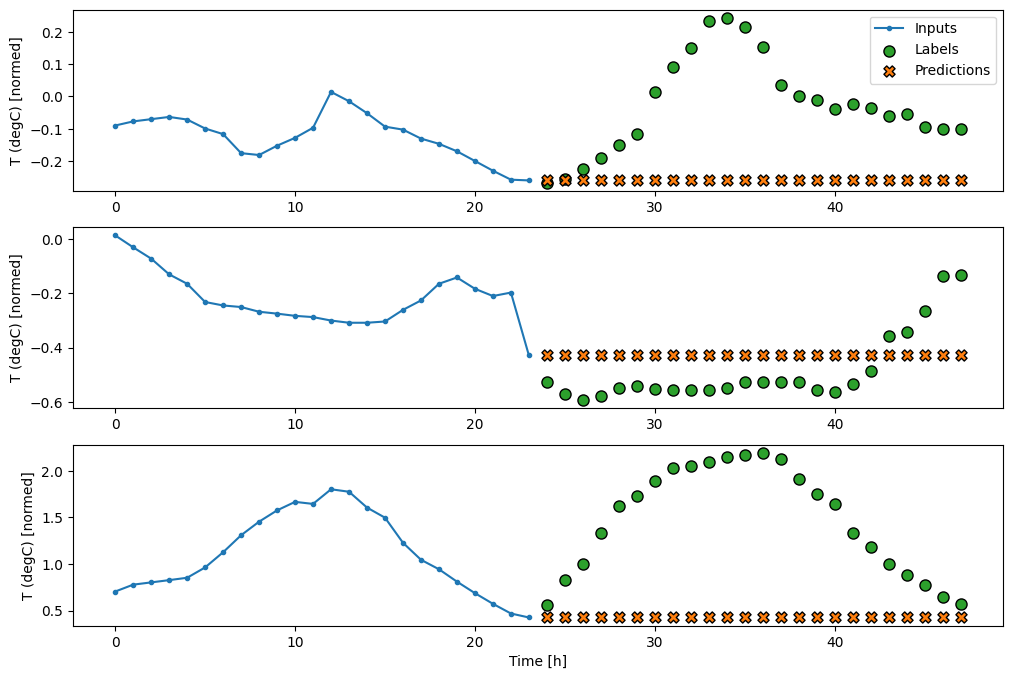
Ponieważ to zadanie polega na przewidzeniu 24 godzin w przyszłość, biorąc pod uwagę 24 godziny z przeszłości, innym prostym podejściem jest powtórzenie poprzedniego dnia, zakładając, że jutro będzie podobnie:
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
Modele jednostrzałowe
Jednym z wysokopoziomowych podejść do tego problemu jest użycie modelu „pojedynczego strzału”, w którym model wykonuje predykcję całej sekwencji w jednym kroku.
Można to skutecznie zaimplementować jako tf.keras.layers.Dense z jednostkami wyjściowymi OUT_STEPS*features . Model musi tylko zmienić kształt tych danych wyjściowych do wymaganych (OUTPUT_STEPS, features) .
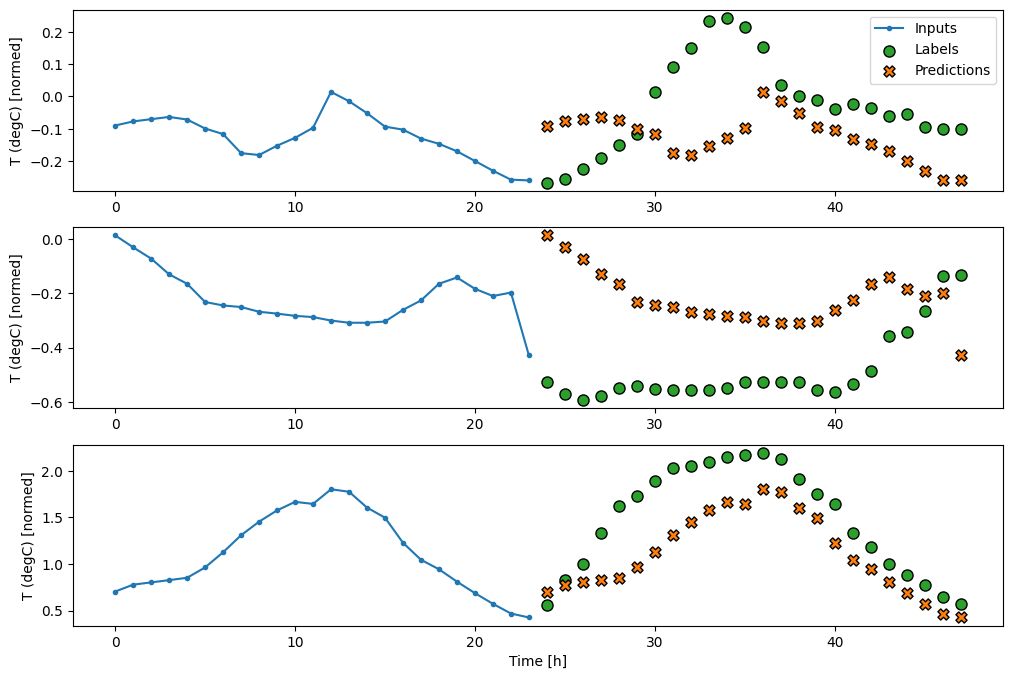
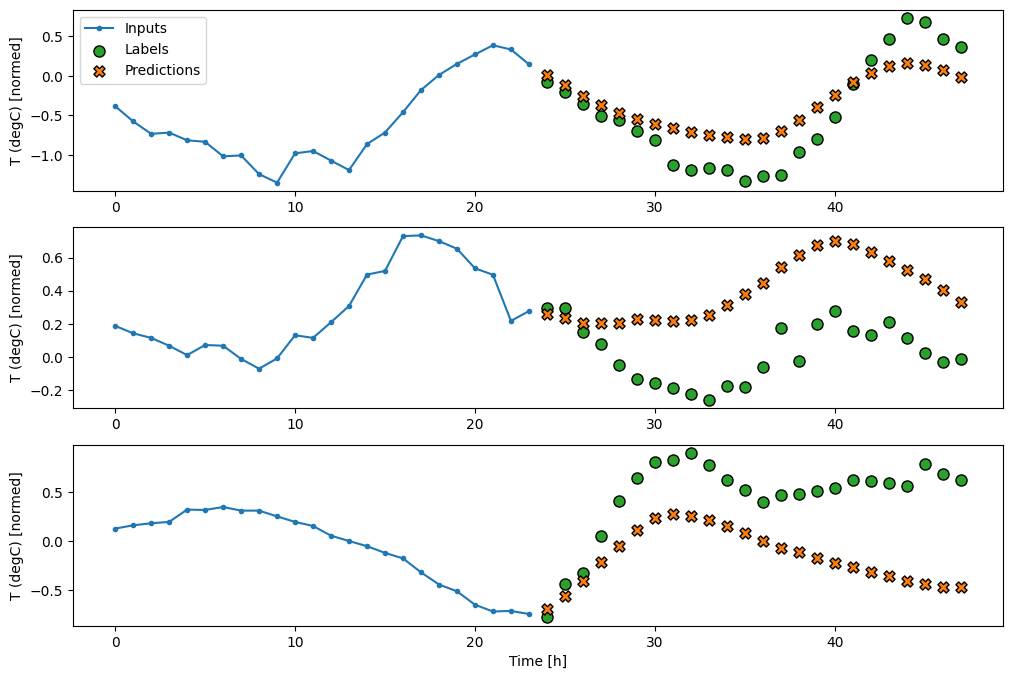
Liniowy
Prosty model liniowy oparty na ostatnim kroku czasu wejściowego działa lepiej niż którykolwiek z modeli bazowych, ale jest słabszy. Model musi przewidywać kroki czasowe OUTPUT_STEPS na podstawie pojedynczego wejściowego kroku czasowego z liniową projekcją. Może uchwycić tylko niskowymiarowy wycinek zachowania, prawdopodobnie oparty głównie na porze dnia i porze roku.
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053
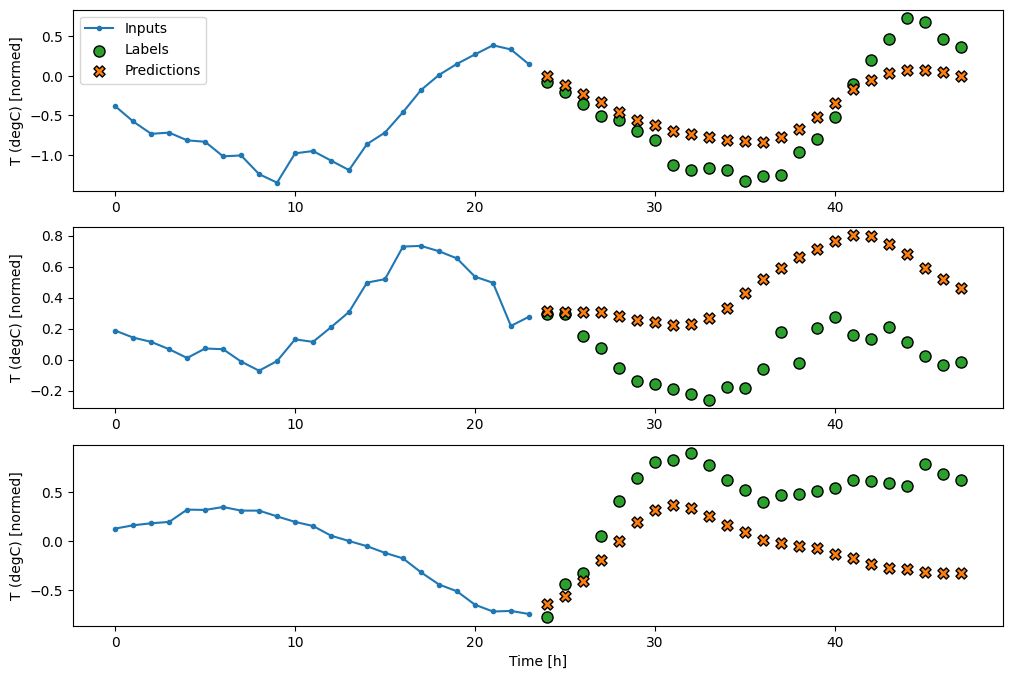
Gęsty
Dodanie tf.keras.layers.Dense między wejściem a wyjściem daje modelowi liniowemu większą moc, ale nadal opiera się tylko na jednym wejściowym kroku czasowym.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
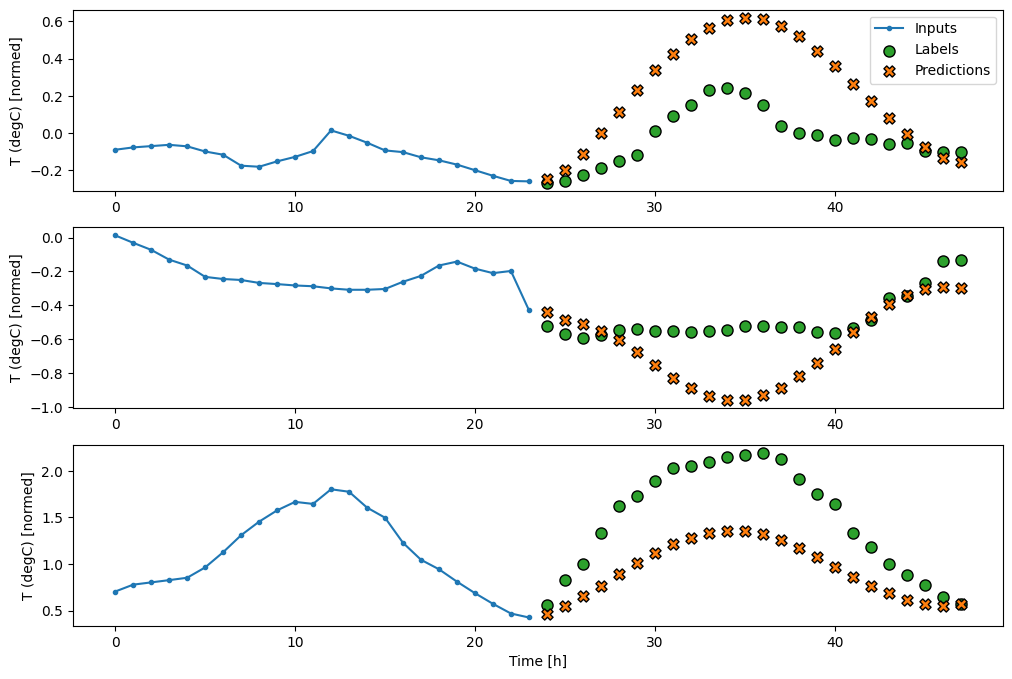
CNN
Model splotowy tworzy prognozy na podstawie historii o stałej szerokości, co może prowadzić do lepszej wydajności niż model gęsty, ponieważ może zobaczyć, jak rzeczy zmieniają się w czasie:
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
RNN
Model cykliczny może nauczyć się korzystać z długiej historii danych wejściowych, jeśli jest to istotne dla prognoz, które wykonuje model. Tutaj model będzie akumulował stan wewnętrzny przez 24 godziny, przed wykonaniem pojedynczej prognozy na następne 24 godziny.
W tym formacie pojedynczego strzału LSTM musi wygenerować dane wyjściowe tylko w ostatnim kroku czasowym, więc ustaw return_sequences=False w tf.keras.layers.LSTM .
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
Zaawansowane: model autoregresyjny
Wszystkie powyższe modele przewidują całą sekwencję wyjściową w jednym kroku.
W niektórych przypadkach pomocne może być rozłożenie przez model tej prognozy na poszczególne kroki czasowe. Następnie dane wyjściowe każdego modelu mogą być wprowadzane z powrotem do siebie na każdym kroku, a prognozy mogą być uzależnione od poprzedniego, jak w klasycznym generowaniu sekwencji z powtarzalnymi sieciami neuronowymi .
Jedną z wyraźnych zalet tego stylu modelu jest to, że można go skonfigurować tak, aby wytwarzał wydruki o różnej długości.
Możesz wziąć dowolny z jednoetapowych modeli wielowyjściowych wytrenowanych w pierwszej połowie tego samouczka i uruchomić w autoregresyjnej pętli sprzężenia zwrotnego, ale tutaj skupisz się na budowaniu modelu, który został wyraźnie przeszkolony w tym celu.
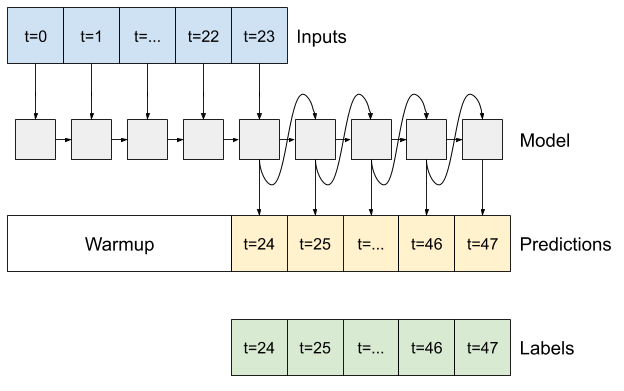
RNN
Ten samouczek buduje tylko autoregresywny model RNN, ale ten wzorzec można zastosować do dowolnego modelu, który został zaprojektowany do wyprowadzania pojedynczego kroku czasowego.
Model będzie miał taką samą podstawową formę, jak wcześniejsze jednoetapowe modele LSTM: warstwę tf.keras.layers.LSTM , po której nastąpi warstwa tf.keras.layers.Dense , która konwertuje dane wyjściowe warstwy LSTM na prognozy modelu.
tf.keras.layers.LSTM to tf.keras.layers.LSTMCell opakowana w tf.keras.layers.RNN wyższego poziomu, która zarządza stanem i wynikami sekwencji (sprawdź Recurrent Neural Networks (RNN) z Keras przewodnik po szczegóły).
W takim przypadku model musi ręcznie zarządzać danymi wejściowymi dla każdego kroku, więc używa tf.keras.layers.LSTMCell bezpośrednio dla interfejsu niższego poziomu z pojedynczym krokiem czasowym.
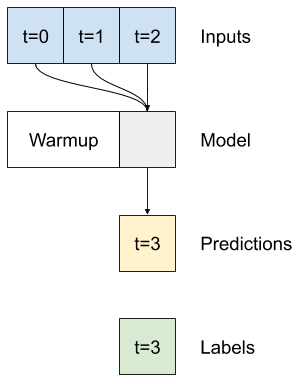
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
Pierwszą metodą, jakiej ten model potrzebuje, jest metoda warmup , aby zainicjować jego stan wewnętrzny na podstawie danych wejściowych. Po przeszkoleniu ten stan przechwyci odpowiednie części historii wejściowej. Jest to odpowiednik wcześniejszego jednoetapowego modelu LSTM :
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
Ta metoda zwraca prognozę z jednym krokiem czasowym i stan wewnętrzny LSTM :
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
Ze stanem RNN i wstępną prognozą możesz teraz kontynuować iterację modelu, podając prognozy na każdym kroku wstecz jako dane wejściowe.
Najprostszym podejściem do zbierania przewidywań wyjściowych jest użycie listy Pythona i tf.stack po pętli.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
Przetestuj ten model na przykładowych wejściach:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
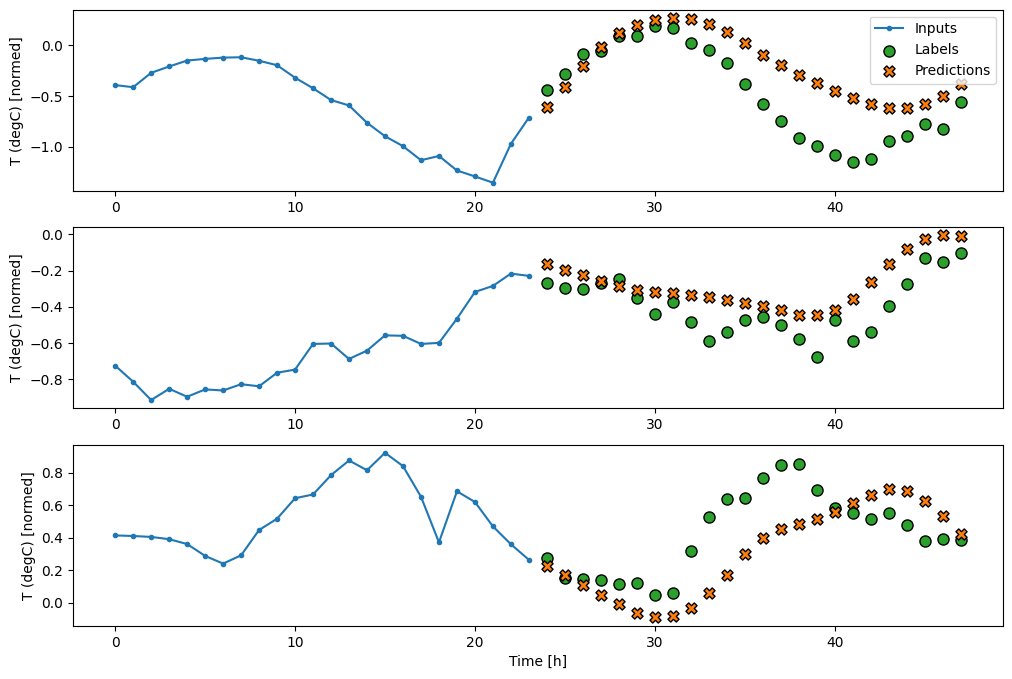
Teraz wytrenuj model:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
Wydajność
W przypadku tego problemu widać wyraźnie malejące zwroty w funkcji złożoności modelu:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()

Metryki modeli wielowyjściowych w pierwszej połowie tego samouczka pokazują wydajność uśrednioną dla wszystkich funkcji wyjściowych. Te osiągi są podobne, ale również uśrednione w wyjściowych krokach czasowych.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
Zyski osiągnięte przy przechodzeniu od modelu gęstego do modeli splotowych i rekurencyjnych wynoszą tylko kilka procent (jeśli w ogóle), a model autoregresyjny wypadł wyraźnie gorzej. Tak więc te bardziej złożone podejścia mogą nie być warte zachodu w tym problemie, ale nie było sposobu, aby się o tym dowiedzieć bez próbowania, a te modele mogą być pomocne w rozwiązaniu problemu.
Następne kroki
Ten samouczek był szybkim wprowadzeniem do prognozowania szeregów czasowych przy użyciu TensorFlow.
Aby dowiedzieć się więcej, zapoznaj się z:
- Rozdział 15 praktycznego uczenia maszynowego za pomocą Scikit-Learn, Keras i TensorFlow , wydanie drugie.
- Rozdział 6 Deep Learning z Pythonem .
- Lekcja 8 z wprowadzenia Udacity do TensorFlow do głębokiego uczenia się , w tym zeszyty ćwiczeń .
Pamiętaj też, że możesz zaimplementować dowolny klasyczny model szeregów czasowych w TensorFlow — ten samouczek skupia się tylko na wbudowanych funkcjach TensorFlow.
