 مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
مقدمه ای بر گرادیان ها و راهنمای تمایز خودکار شامل همه چیزهایی است که برای محاسبه گرادیان در TensorFlow لازم است. این راهنما بر روی ویژگیهای عمیقتر و کمتر رایج API tf.GradientTape دارد.
برپایی
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
کنترل ضبط گرادیان
در راهنمای تمایز خودکار ، نحوه کنترل متغیرها و تانسورها را در هنگام ساخت محاسبه گرادیان مشاهده کردید.
نوار همچنین روش هایی برای دستکاری ضبط دارد.
ضبط را متوقف کنید
اگر میخواهید ضبط گرادیانها را متوقف کنید، میتوانید از tf.GradientTape.stop_recording برای تعلیق موقت ضبط استفاده کنید.
اگر نمیخواهید یک عملیات پیچیده را در وسط مدل خود متمایز کنید، این ممکن است برای کاهش سربار مفید باشد. این می تواند شامل محاسبه یک متریک یا یک نتیجه میانی باشد:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
بازنشانی/شروع ضبط از ابتدا
اگر میخواهید کاملاً از نو شروع کنید، از tf.GradientTape.reset استفاده کنید. معمولاً خواندن سادهتر از بلوک نوار گرادیان و راهاندازی مجدد آسانتر است، اما زمانی که خروج از نوار نوار دشوار یا غیرممکن است، میتوانید از روش reset استفاده کنید.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
جریان گرادیان را با دقت متوقف کنید
برخلاف کنترلهای نوار سراسری بالا، تابع tf.stop_gradient بسیار دقیقتر است. می توان از آن برای جلوگیری از جریان شیب ها در یک مسیر خاص، بدون نیاز به دسترسی به خود نوار استفاده کرد:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
گرادیان های سفارشی
در برخی موارد، ممکن است بخواهید دقیقاً نحوه محاسبه گرادیان ها را به جای استفاده از پیش فرض کنترل کنید. این موقعیت ها عبارتند از:
- هیچ گرادیان تعریف شده ای برای عملیات جدیدی که در حال نوشتن آن هستید وجود ندارد.
- محاسبات پیش فرض از نظر عددی ناپایدار هستند.
- شما می خواهید یک محاسبات گران قیمت را از طریق پاس رو به جلو ذخیره کنید.
- شما می خواهید یک مقدار را تغییر دهید (به عنوان مثال، با استفاده از
tf.clip_by_valueیاtf.math.round) بدون تغییر گرادیان.
برای اولین مورد، برای نوشتن یک op جدید، میتوانید از tf.RegisterGradient برای تنظیم خود استفاده کنید (برای جزئیات به اسناد API مراجعه کنید). (توجه داشته باشید که رجیستری گرادیان جهانی است، بنابراین آن را با احتیاط تغییر دهید.)
برای سه مورد آخر، می توانید از tf.custom_gradient استفاده کنید.
در اینجا یک مثال است که tf.clip_by_norm را برای گرادیان متوسط اعمال می کند:
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
برای جزئیات بیشتر به اسناد tf.custom_gradient decorator API مراجعه کنید.
گرادیان های سفارشی در SavedModel
شیب های سفارشی را می توان با استفاده از گزینه tf.saved_model.SaveOptions(experimental_custom_gradients=True) در SavedModel ذخیره کرد.
برای ذخیره شدن در SavedModel، تابع گرادیان باید قابل ردیابی باشد (برای کسب اطلاعات بیشتر، راهنمای عملکرد بهتر با tf.function را بررسی کنید).
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Assets written to: saved_model/assets tf.Tensor(2.0, shape=(), dtype=float32)
نکته ای در مورد مثال بالا: اگر سعی کنید کد بالا را با tf.saved_model.SaveOptions(experimental_custom_gradients=False) جایگزین کنید، گرادیان همچنان همان نتیجه را هنگام بارگیری ایجاد می کند. دلیل آن این است که رجیستری گرادیان همچنان شامل گرادیان سفارشی مورد استفاده در تابع call_custom_op است. با این حال، اگر پس از ذخیره کردن بدون شیب سفارشی، زمان اجرا را مجدداً راه اندازی کنید، اجرای مدل بارگذاری شده در زیر tf.GradientTape این خطا را نشان می دهد: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .
نوارهای متعدد
چندین نوار به طور یکپارچه با هم تعامل دارند.
به عنوان مثال، در اینجا هر نوار مجموعه متفاوتی از تانسورها را تماشا می کند:
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
گرادیان های مرتبه بالاتر
عملیات داخل مدیر زمینه tf.GradientTape برای تمایز خودکار ثبت می شود. اگر گرادیان ها در آن زمینه محاسبه شوند، محاسبه گرادیان نیز ثبت می شود. در نتیجه، دقیقاً همان API برای گرادیان های مرتبه بالاتر نیز کار می کند.
مثلا:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0 d2y_dx2: 6.0
در حالی که این مشتق دوم یک تابع اسکالر را به شما می دهد، این الگو برای تولید یک ماتریس هسی تعمیم نمی یابد، زیرا tf.GradientTape.gradient فقط گرادیان یک اسکالر را محاسبه می کند. برای ساختن یک ماتریس هسی ، به مثال هسی زیر بخش ژاکوبین بروید.
"تماسهای تودرتو به tf.GradientTape.gradient " یک الگوی خوب است زمانی که شما یک اسکالر را از یک گرادیان محاسبه می کنید، و سپس اسکالر به دست آمده به عنوان منبعی برای محاسبه گرادیان دوم عمل می کند، مانند مثال زیر.
مثال: تنظیم گرادیان ورودی
بسیاری از مدل ها مستعد "نمونه های متخاصم" هستند. این مجموعه از تکنیک ها ورودی مدل را تغییر می دهد تا خروجی مدل را اشتباه بگیرد. ساده ترین پیاده سازی - مانند مثال Adversarial با استفاده از حمله Fast Gradient Signed Method - یک گام در امتداد گرادیان خروجی با توجه به ورودی انجام می دهد. " گرادیان ورودی".
یکی از تکنیکهای افزایش استحکام به نمونههای متخاصم، منظمسازی گرادیان ورودی است (Finlay & Oberman, 2019)، که تلاش میکند تا اندازه گرادیان ورودی را به حداقل برساند. اگر گرادیان ورودی کوچک است، تغییر در خروجی نیز باید کم باشد.
در زیر یک پیاده سازی ساده از تنظیم گرادیان ورودی ارائه شده است. اجرا عبارت است از:
- شیب خروجی را با توجه به ورودی با استفاده از نوار داخلی محاسبه کنید.
- بزرگی آن گرادیان ورودی را محاسبه کنید.
- شیب آن قدر را با توجه به مدل محاسبه کنید.
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
یعقوبیان
تمام مثالهای قبلی گرادیانهای یک هدف اسکالر را با توجه به برخی از تانسورها (ها) منبع گرفته بودند.
ماتریس ژاکوبین گرادیان های یک تابع با ارزش برداری را نشان می دهد. هر ردیف شامل گرادیان یکی از عناصر بردار است.
روش tf.GradientTape.jacobian به شما این امکان را می دهد که ماتریس Jacobian را به طور موثر محاسبه کنید.
توجه داشته باشید که:
- مانند
gradient: آرگومانsourcesمی تواند یک تانسور یا یک ظرف تانسور باشد. - برخلاف
gradient: تانسورtargetباید یک تانسور منفرد باشد.
منبع اسکالر
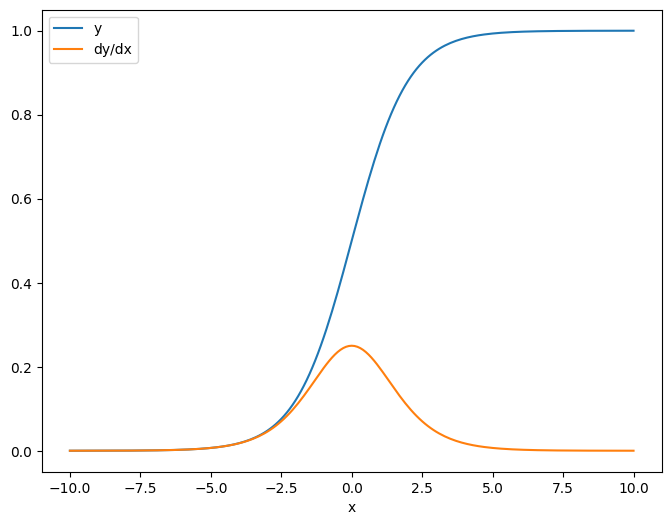
به عنوان اولین مثال، در اینجا ژاکوبین یک بردار-هدف با توجه به یک منبع اسکالر است.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
وقتی ژاکوبین را با توجه به یک اسکالر می گیرید، نتیجه شکل هدف را دارد و گرادیان هر عنصر را نسبت به منبع نشان می دهد:
print(y.shape)
print(dy_dx.shape)
(201,) (201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
منبع تانسور
چه ورودی اسکالر یا تانسور باشد، tf.GradientTape.jacobian به طور موثر گرادیان هر عنصر منبع را با توجه به هر عنصر هدف(ها) محاسبه می کند.
به عنوان مثال، خروجی این لایه دارای شکل (10, 7) :
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
و شکل هسته لایه (5, 10) است:
layer.kernel.shape
TensorShape([5, 10])
شکل ژاکوبین خروجی نسبت به هسته آن دو شکل است که به هم پیوسته اند:
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
اگر ابعاد هدف را جمع آوری کنید، با گرادیان مجموع که توسط tf.GradientTape.gradient محاسبه می شد باقی می ماند:
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10) delta: 2.3841858e-07
مثال: هسیان
در حالی که tf.GradientTape روش صریحی برای ساخت یک ماتریس Hessian ارائه نمی دهد، می توان آن را با استفاده از روش tf.GradientTape.jacobian ساخت.
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8) h.shape: (5, 8, 5, 8)
برای استفاده از این هسین برای گام روش نیوتن ، ابتدا محورهای آن را به یک ماتریس مسطح کرده و گرادیان را به یک بردار صاف کنید:
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
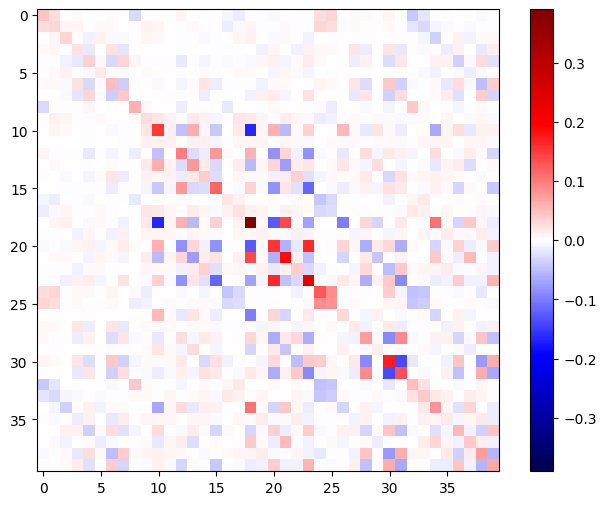
ماتریس هسین باید متقارن باشد:
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
مرحله به روز رسانی روش نیوتن در زیر نشان داده شده است:
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
در حالی که این برای یک tf.Variable منفرد نسبتاً ساده است، استفاده از آن برای یک مدل غیر پیش پا افتاده نیاز به الحاق و برش دقیق برای تولید یک Hessian کامل در بین چندین متغیر دارد.
دسته ژاکوبین
در برخی موارد، شما می خواهید ژاکوبین هر یک از یک پشته از اهداف را با توجه به پشته ای از منابع بگیرید، جایی که ژاکوبین ها برای هر جفت هدف-منبع مستقل هستند.
به عنوان مثال، در اینجا ورودی x شکل میگیرد (batch, ins) و خروجی y شکل (batch, outs) :
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
ژاکوبین کامل y نسبت به x شکلی از (batch, ins, batch, outs) دارد، حتی اگر فقط بخواهید (batch, ins, outs) :
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
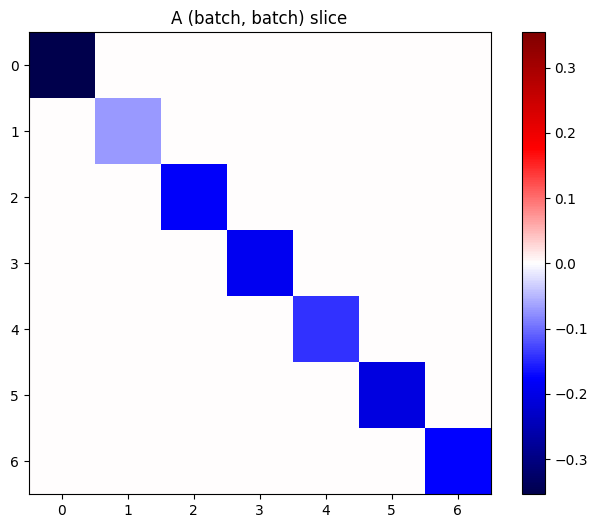
اگر گرادیان هر آیتم در پشته مستقل باشد، هر برش (batch, batch) از این تانسور یک ماتریس مورب است:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
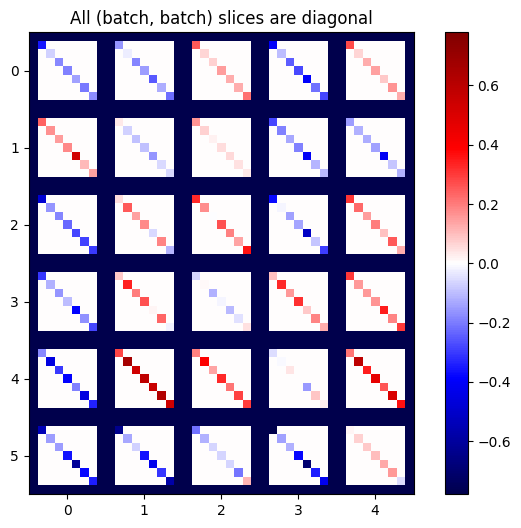
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
برای به دست آوردن نتیجه دلخواه، می توانید بر روی بعد batch تکراری جمع کنید، یا در غیر این صورت قطرها را با استفاده از tf.einsum انتخاب کنید:
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5) (7, 6, 5)
انجام محاسبات بدون بعد اضافی در وهله اول بسیار کارآمدتر خواهد بود. روش tf.GradientTape.batch_jacobian دقیقاً این کار را انجام می دهد:
jb = tape.batch_jacobian(y, x)
jb.shape
WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. j.shape: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
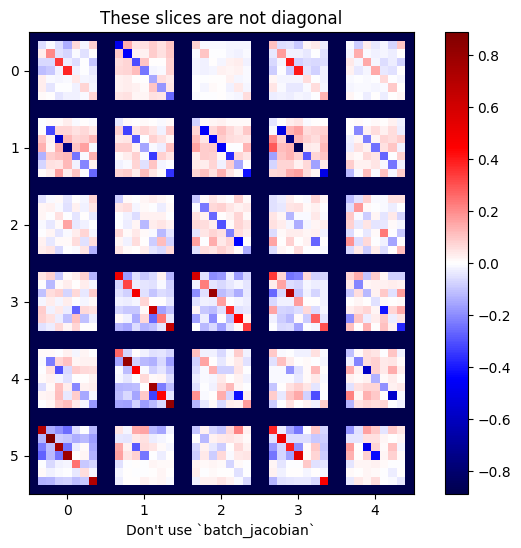
در این مورد، batch_jacobian همچنان اجرا میشود و چیزی را با شکل مورد انتظار برمیگرداند، اما محتوای آن معنای نامشخصی دارد:
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)
