 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
W zadaniu regresji celem jest przewidzenie wyniku wartości ciągłej, takiej jak cena lub prawdopodobieństwo. Porównaj to z problemem klasyfikacji , w którym celem jest wybranie klasy z listy klas (na przykład, gdy obraz zawiera jabłko lub pomarańczę, rozpoznanie, który owoc znajduje się na obrazku).
Ten samouczek wykorzystuje klasyczny zestaw danych Auto MPG i pokazuje, jak budować modele do przewidywania zużycia paliwa w samochodach z końca lat 70. i początku lat 80. XX wieku. W tym celu podasz modele z opisem wielu samochodów z tamtego okresu. Ten opis obejmuje takie atrybuty, jak cylindry, pojemność skokowa, moc i waga.
W tym przykładzie zastosowano interfejs API Keras. (Odwiedź samouczki i przewodniki Keras, aby dowiedzieć się więcej.)
# Use seaborn for pairplot.pip install -q seaborn
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# Make NumPy printouts easier to read.
np.set_printoptions(precision=3, suppress=True)
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
2.8.0-rc1
Zestaw danych Auto MPG
Zestaw danych jest dostępny w repozytorium UCI Machine Learning Repository .
Pobierz dane
Najpierw pobierz i zaimportuj zestaw danych za pomocą pand:
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
column_names = ['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(url, names=column_names,
na_values='?', comment='\t',
sep=' ', skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
Wyczyść dane
Zbiór danych zawiera kilka nieznanych wartości:
dataset.isna().sum()
MPG 0 Cylinders 0 Displacement 0 Horsepower 6 Weight 0 Acceleration 0 Model Year 0 Origin 0 dtype: int64
Upuść te wiersze, aby ten wstępny samouczek był prosty:
dataset = dataset.dropna()
Kolumna "Origin" ma charakter kategoryczny, a nie liczbowy. Następnym krokiem jest więc jednokrotne zakodowanie wartości w kolumnie za pomocą pd.get_dummies .
dataset['Origin'] = dataset['Origin'].map({1: 'USA', 2: 'Europe', 3: 'Japan'})
dataset = pd.get_dummies(dataset, columns=['Origin'], prefix='', prefix_sep='')
dataset.tail()
Podziel dane na zestawy treningowe i testowe
Teraz podziel zestaw danych na zestaw uczący i zestaw testowy. Zestaw testowy wykorzystasz w końcowej ocenie swoich modeli.
train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)
Sprawdź dane
Przejrzyj łączny rozkład kilku par kolumn ze zbioru uczącego.
Górny rząd sugeruje, że efektywność paliwowa (MPG) jest funkcją wszystkich pozostałych parametrów. Pozostałe wiersze wskazują, że są one funkcjami siebie nawzajem.
sns.pairplot(train_dataset[['MPG', 'Cylinders', 'Displacement', 'Weight']], diag_kind='kde')
<seaborn.axisgrid.PairGrid at 0x7f6bfdae9850>

Sprawdźmy też ogólne statystyki. Zwróć uwagę, że każda funkcja obejmuje bardzo inny zakres:
train_dataset.describe().transpose()
Podziel funkcje z etykiet
Oddziel wartość docelową — „etykietę” — od funkcji. Ta etykieta jest wartością, której przewidywania będziesz trenował model.
train_features = train_dataset.copy()
test_features = test_dataset.copy()
train_labels = train_features.pop('MPG')
test_labels = test_features.pop('MPG')
Normalizacja
W tabeli statystyk łatwo zobaczyć, jak różne są zakresy poszczególnych funkcji:
train_dataset.describe().transpose()[['mean', 'std']]
Dobrą praktyką jest normalizowanie funkcji, które używają różnych skal i zakresów.
Jednym z powodów, dla których jest to ważne, jest to, że cechy są mnożone przez wagi modelu. Tak więc skala wyjść i skala gradientów zależy od skali wejść.
Chociaż model może być zbieżny bez normalizacji funkcji, normalizacja sprawia, że szkolenie jest znacznie bardziej stabilne.
Warstwa normalizacji
tf.keras.layers.Normalization to czysty i prosty sposób na dodanie normalizacji funkcji do modelu.
Pierwszym krokiem jest stworzenie warstwy:
normalizer = tf.keras.layers.Normalization(axis=-1)
Następnie dopasuj stan warstwy przetwarzania wstępnego do danych, wywołując Normalization.adapt :
normalizer.adapt(np.array(train_features))
Oblicz średnią i wariancję i zapisz je w warstwie:
print(normalizer.mean.numpy())
[[ 5.478 195.318 104.869 2990.252 15.559 75.898 0.178 0.197
0.624]]
Gdy warstwa jest wywoływana, zwraca dane wejściowe, przy czym każdy element jest niezależnie znormalizowany:
first = np.array(train_features[:1])
with np.printoptions(precision=2, suppress=True):
print('First example:', first)
print()
print('Normalized:', normalizer(first).numpy())
First example: [[ 4. 90. 75. 2125. 14.5 74. 0. 0. 1. ]] Normalized: [[-0.87 -1.01 -0.79 -1.03 -0.38 -0.52 -0.47 -0.5 0.78]]
Regresja liniowa
Przed zbudowaniem głębokiego modelu sieci neuronowej zacznij od regresji liniowej z wykorzystaniem jednej i kilku zmiennych.
Regresja liniowa z jedną zmienną
Rozpocznij od regresji liniowej z jedną zmienną, aby przewidzieć 'MPG' z 'Horsepower' .
Trenowanie modelu za pomocą tf.keras zwykle rozpoczyna się od zdefiniowania architektury modelu. Użyj modelu tf.keras.Sequential , który reprezentuje sekwencję kroków .
Model regresji liniowej z jedną zmienną składa się z dwóch etapów:
- Normalizuj funkcje wejściowe
'Horsepower'za pomocą warstwy przetwarzania wstępnegotf.keras.layers.Normalization. - Zastosuj transformację liniową (\(y = mx+b\)), aby uzyskać 1 wynik przy użyciu warstwy liniowej (
tf.keras.layers.Dense).
Liczbę danych wejściowych można ustawić za pomocą argumentu input_shape lub automatycznie, gdy model jest uruchamiany po raz pierwszy.
Najpierw utwórz tablicę NumPy utworzoną z funkcji 'Horsepower' . Następnie utwórz instancję tf.keras.layers.Normalization i dopasuj jej stan do danych dotyczących horsepower :
horsepower = np.array(train_features['Horsepower'])
horsepower_normalizer = layers.Normalization(input_shape=[1,], axis=None)
horsepower_normalizer.adapt(horsepower)
Zbuduj model Keras Sequential:
horsepower_model = tf.keras.Sequential([
horsepower_normalizer,
layers.Dense(units=1)
])
horsepower_model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense (Dense) (None, 1) 2
=================================================================
Total params: 5
Trainable params: 2
Non-trainable params: 3
_________________________________________________________________
Model ten przewiduje 'MPG' z 'Horsepower' .
Uruchom nieprzeszkolony model na pierwszych 10 wartościach „Moc”. Wynik nie będzie dobry, ale zauważ, że ma oczekiwany kształt (10, 1) :
horsepower_model.predict(horsepower[:10])
array([[-1.186],
[-0.67 ],
[ 2.189],
[-1.662],
[-1.504],
[-0.59 ],
[-1.782],
[-1.504],
[-0.392],
[-0.67 ]], dtype=float32)
Po skompilowaniu modelu skonfiguruj procedurę uczenia przy użyciu metody Keras Model.compile . Najważniejszymi argumentami do kompilacji są loss i optimizer , ponieważ definiują one, co zostanie zoptymalizowane ( mean_absolute_error ) i jak (za pomocą tf.keras.optimizers.Adam ).
horsepower_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
Użyj Keras Model.fit , aby przeprowadzić szkolenie dla 100 epok:
%%time
history = horsepower_model.fit(
train_features['Horsepower'],
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.79 s, sys: 797 ms, total: 5.59 s Wall time: 3.8 s
Wizualizuj postęp treningu modelu za pomocą statystyk przechowywanych w obiekcie history :
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_loss(history):
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.ylim([0, 10])
plt.xlabel('Epoch')
plt.ylabel('Error [MPG]')
plt.legend()
plt.grid(True)
plot_loss(history)
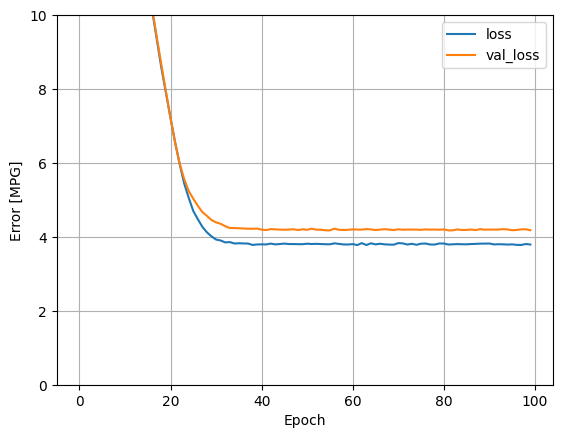
Zbierz wyniki na zestawie testowym na później:
test_results = {}
test_results['horsepower_model'] = horsepower_model.evaluate(
test_features['Horsepower'],
test_labels, verbose=0)
Ponieważ jest to regresja z pojedynczą zmienną, łatwo jest wyświetlić prognozy modelu jako funkcję danych wejściowych:
x = tf.linspace(0.0, 250, 251)
y = horsepower_model.predict(x)
def plot_horsepower(x, y):
plt.scatter(train_features['Horsepower'], train_labels, label='Data')
plt.plot(x, y, color='k', label='Predictions')
plt.xlabel('Horsepower')
plt.ylabel('MPG')
plt.legend()
plot_horsepower(x, y)
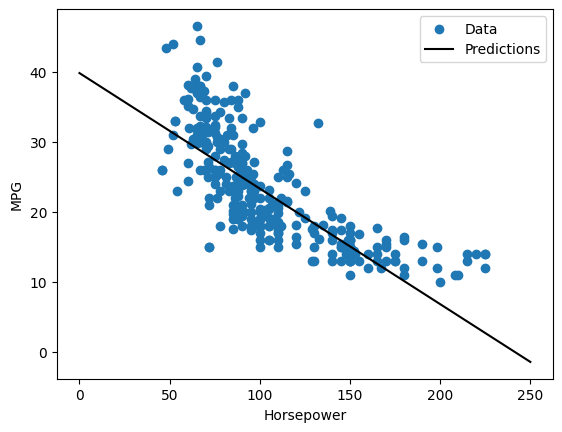
Regresja liniowa z wieloma danymi wejściowymi
Możesz użyć prawie identycznej konfiguracji, aby przewidywać na podstawie wielu danych wejściowych. Ten model nadal wykonuje to samo \(y = mx+b\) z wyjątkiem tego, że \(m\) jest macierzą, a \(b\) jest wektorem.
Ponownie utwórz dwuetapowy model Keras Sequential z pierwszą warstwą będącą normalizer ( tf.keras.layers.Normalization(axis=-1) ) zdefiniowaną wcześniej i zaadaptowaną do całego zestawu danych:
linear_model = tf.keras.Sequential([
normalizer,
layers.Dense(units=1)
])
Kiedy wywołujesz Model.predict dla partii danych wejściowych, generuje units=1 wyjścia dla każdego przykładu:
linear_model.predict(train_features[:10])
array([[ 0.441],
[ 1.522],
[ 0.188],
[ 1.169],
[ 0.058],
[ 0.965],
[ 0.034],
[-0.674],
[ 0.437],
[-0.37 ]], dtype=float32)
Kiedy wywołasz model, zbudowane zostaną jego macierze wag — sprawdź, czy wagi kernel ( \(m\) w \(y=mx+b\)) mają kształt (9, 1) :
linear_model.layers[1].kernel
<tf.Variable 'dense_1/kernel:0' shape=(9, 1) dtype=float32, numpy=
array([[-0.702],
[ 0.307],
[ 0.114],
[ 0.233],
[ 0.244],
[ 0.322],
[-0.725],
[-0.151],
[ 0.407]], dtype=float32)>
Skonfiguruj model za pomocą Keras Model.compile i trenuj za pomocą Model.fit przez 100 epok:
linear_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
%%time
history = linear_model.fit(
train_features,
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.89 s, sys: 740 ms, total: 5.63 s Wall time: 3.75 s
Użycie wszystkich danych wejściowych w tym modelu regresji pozwala uzyskać znacznie niższy błąd uczenia i walidacji niż model horsepower_model , który miał jedno dane wejściowe:
plot_loss(history)
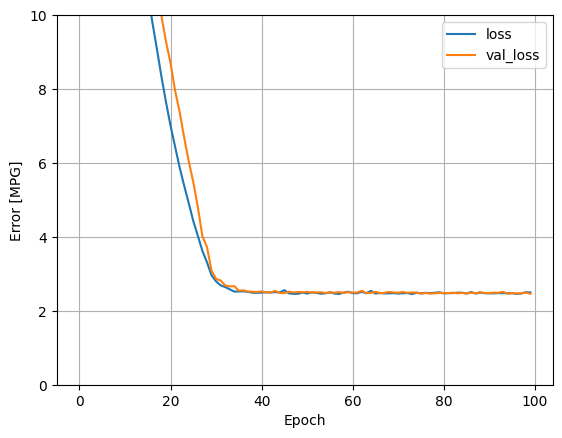
Zbierz wyniki na zestawie testowym na później:
test_results['linear_model'] = linear_model.evaluate(
test_features, test_labels, verbose=0)
Regresja z głęboką siecią neuronową (DNN)
W poprzedniej sekcji zaimplementowano dwa modele liniowe dla jednego i wielu danych wejściowych.
Tutaj zaimplementujesz jednowejściowe i wielowejściowe modele DNN.
Kod jest zasadniczo taki sam, z wyjątkiem tego, że model został rozszerzony o niektóre „ukryte” warstwy nieliniowe. Nazwa „ukryty” oznacza tutaj po prostu niepodłączony bezpośrednio do wejść lub wyjść.
Modele te będą zawierać o kilka więcej warstw niż model liniowy:
- Warstwa normalizacji, jak poprzednio (z
horsepower_normalizerdla modelu z jednym wejściem inormalizerdla modelu z wieloma wejściami). - Dwie ukryte, nieliniowe,
Densewarstwy z nieliniowością funkcji aktywacjirelu(relu). - Liniowa,
Dense, jednowyjściowa warstwa.
Oba modele będą używać tej samej procedury uczenia, więc metoda compile jest zawarta w poniższej funkcji build_and_compile_model .
def build_and_compile_model(norm):
model = keras.Sequential([
norm,
layers.Dense(64, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
model.compile(loss='mean_absolute_error',
optimizer=tf.keras.optimizers.Adam(0.001))
return model
Regresja z użyciem DNN i pojedynczego wejścia
Utwórz model DNN z tylko 'Horsepower' jako danymi wejściowymi i horsepower_normalizer (zdefiniowanym wcześniej) jako warstwą normalizacji:
dnn_horsepower_model = build_and_compile_model(horsepower_normalizer)
Model ten ma znacznie więcej parametrów, które można trenować niż modele liniowe:
dnn_horsepower_model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense_2 (Dense) (None, 64) 128
dense_3 (Dense) (None, 64) 4160
dense_4 (Dense) (None, 1) 65
=================================================================
Total params: 4,356
Trainable params: 4,353
Non-trainable params: 3
_________________________________________________________________
Trenuj model z Keras Model.fit :
%%time
history = dnn_horsepower_model.fit(
train_features['Horsepower'],
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.07 s, sys: 691 ms, total: 5.76 s Wall time: 3.92 s
Ten model działa nieco lepiej niż liniowy model z jednym wejściem horsepower_model :
plot_loss(history)
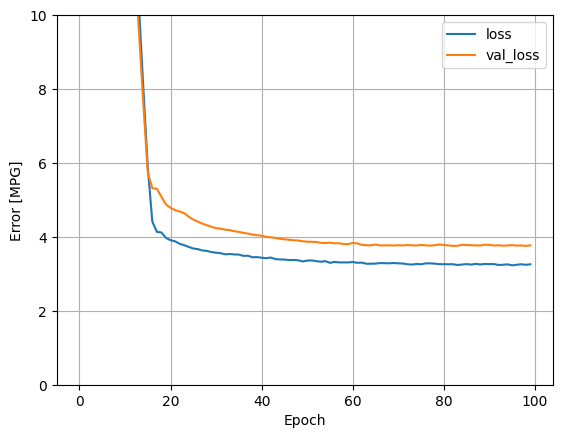
Jeśli wykreślisz prognozy jako funkcję 'Horsepower' , powinieneś zauważyć, w jaki sposób ten model wykorzystuje nieliniowość zapewnianą przez ukryte warstwy:
x = tf.linspace(0.0, 250, 251)
y = dnn_horsepower_model.predict(x)
plot_horsepower(x, y)
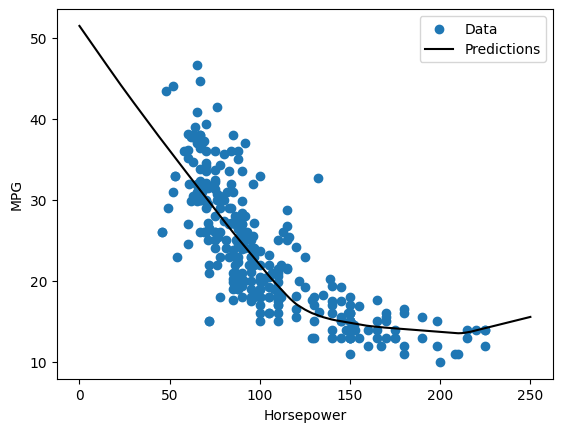
Zbierz wyniki na zestawie testowym na później:
test_results['dnn_horsepower_model'] = dnn_horsepower_model.evaluate(
test_features['Horsepower'], test_labels,
verbose=0)
Regresja przy użyciu DNN i wielu danych wejściowych
Powtórz poprzedni proces, używając wszystkich danych wejściowych. Wydajność modelu nieznacznie poprawia się w zestawie danych walidacyjnych.
dnn_model = build_and_compile_model(normalizer)
dnn_model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization (Normalizatio (None, 9) 19
n)
dense_5 (Dense) (None, 64) 640
dense_6 (Dense) (None, 64) 4160
dense_7 (Dense) (None, 1) 65
=================================================================
Total params: 4,884
Trainable params: 4,865
Non-trainable params: 19
_________________________________________________________________
%%time
history = dnn_model.fit(
train_features,
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.08 s, sys: 725 ms, total: 5.8 s Wall time: 3.94 s
plot_loss(history)
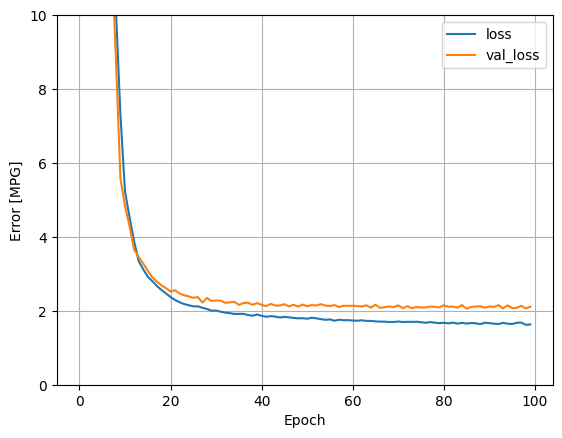
Zbierz wyniki na zestawie testowym:
test_results['dnn_model'] = dnn_model.evaluate(test_features, test_labels, verbose=0)
Wydajność
Ponieważ wszystkie modele zostały przeszkolone, możesz przejrzeć ich wydajność zestawu testowego:
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
Wyniki te pokrywają się z błędem walidacji zaobserwowanym podczas treningu.
Prognozować
Możesz teraz dokonywać prognoz za pomocą modelu dnn_model na zestawie testowym za pomocą Keras Model.predict i przeglądać straty:
test_predictions = dnn_model.predict(test_features).flatten()
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
lims = [0, 50]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)

Wydaje się, że model prognozuje dość dobrze.
Teraz sprawdź rozkład błędów:
error = test_predictions - test_labels
plt.hist(error, bins=25)
plt.xlabel('Prediction Error [MPG]')
_ = plt.ylabel('Count')
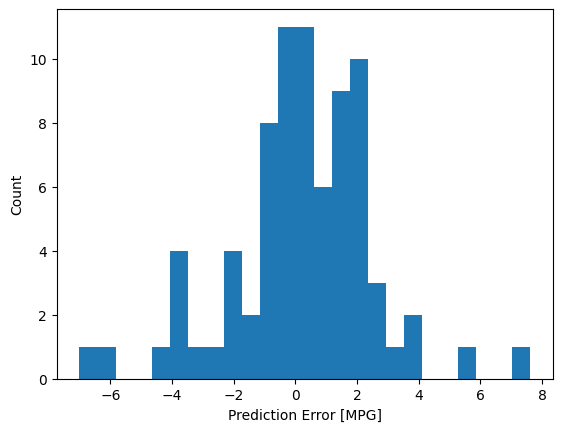
Jeśli jesteś zadowolony z modelu, zapisz go do późniejszego wykorzystania w Model.save :
dnn_model.save('dnn_model')
2022-01-26 07:26:13.372245: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: dnn_model/assets
Jeśli przeładujesz model, daje to identyczne wyniki:
reloaded = tf.keras.models.load_model('dnn_model')
test_results['reloaded'] = reloaded.evaluate(
test_features, test_labels, verbose=0)
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
Wniosek
W tym notatniku wprowadzono kilka technik radzenia sobie z problemem regresji. Oto kilka dodatkowych wskazówek, które mogą pomóc:
- Średnio-kwadratowy błąd (MSE) (
tf.losses.MeanSquaredError) i średni bezwzględny błąd (MAE) (tf.losses.MeanAbsoluteError) są typowymi funkcjami straty używanymi do rozwiązywania problemów z regresją. MAE jest mniej wrażliwy na wartości odstające. Różne funkcje strat są używane do problemów klasyfikacji. - Podobnie metryki oceny używane do regresji różnią się od klasyfikacji.
- Gdy numeryczne cechy danych wejściowych mają wartości o różnych zakresach, każda funkcja powinna być niezależnie skalowana do tego samego zakresu.
- Overfitting jest powszechnym problemem w modelach DNN, chociaż nie stanowił problemu w tym samouczku. Odwiedź samouczek Overfit i underfit, aby uzyskać więcej pomocy w tym zakresie.
# MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
