 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza l'origine su GitHub Visualizza l'origine su GitHub |  Scarica quaderno Scarica quaderno |
In un problema di regressione , l'obiettivo è prevedere l'output di un valore continuo, come un prezzo o una probabilità. Confrontalo con un problema di classificazione , in cui lo scopo è selezionare una classe da un elenco di classi (ad esempio, dove un'immagine contiene una mela o un'arancia, riconoscendo quale frutto è nell'immagine).
Questo tutorial utilizza il classico set di dati Auto MPG e mostra come costruire modelli per prevedere l'efficienza del carburante delle automobili della fine degli anni '70 e dell'inizio degli anni '80. Per fare ciò, fornirai ai modelli una descrizione di molte automobili di quel periodo. Questa descrizione include attributi come cilindri, cilindrata, potenza e peso.
Questo esempio usa l'API Keras. (Per saperne di più, visita i tutorial e le guide di Keras.)
# Use seaborn for pairplot.pip install -q seaborn
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# Make NumPy printouts easier to read.
np.set_printoptions(precision=3, suppress=True)
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
2.8.0-rc1
Il set di dati Auto MPG
Il set di dati è disponibile nell'UCI Machine Learning Repository .
Ottieni i dati
Per prima cosa scarica e importa il set di dati usando Panda:
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
column_names = ['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(url, names=column_names,
na_values='?', comment='\t',
sep=' ', skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
Pulisci i dati
Il set di dati contiene alcuni valori sconosciuti:
dataset.isna().sum()
MPG 0 Cylinders 0 Displacement 0 Horsepower 6 Weight 0 Acceleration 0 Model Year 0 Origin 0 dtype: int64
Rilascia quelle righe per mantenere semplice questo tutorial iniziale:
dataset = dataset.dropna()
La colonna "Origin" è categoriale, non numerica. Quindi il passaggio successivo consiste nel codificare a caldo i valori nella colonna con pd.get_dummies .
dataset['Origin'] = dataset['Origin'].map({1: 'USA', 2: 'Europe', 3: 'Japan'})
dataset = pd.get_dummies(dataset, columns=['Origin'], prefix='', prefix_sep='')
dataset.tail()
Suddividi i dati in set di training e test
Ora suddividi il set di dati in un set di addestramento e un set di test. Utilizzerai il set di test nella valutazione finale dei tuoi modelli.
train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)
Ispeziona i dati
Esaminare la distribuzione congiunta di alcune coppie di colonne del training set.
La riga superiore suggerisce che l'efficienza del carburante (MPG) è una funzione di tutti gli altri parametri. Le altre righe indicano che sono funzioni l'una dell'altra.
sns.pairplot(train_dataset[['MPG', 'Cylinders', 'Displacement', 'Weight']], diag_kind='kde')
<seaborn.axisgrid.PairGrid at 0x7f6bfdae9850>
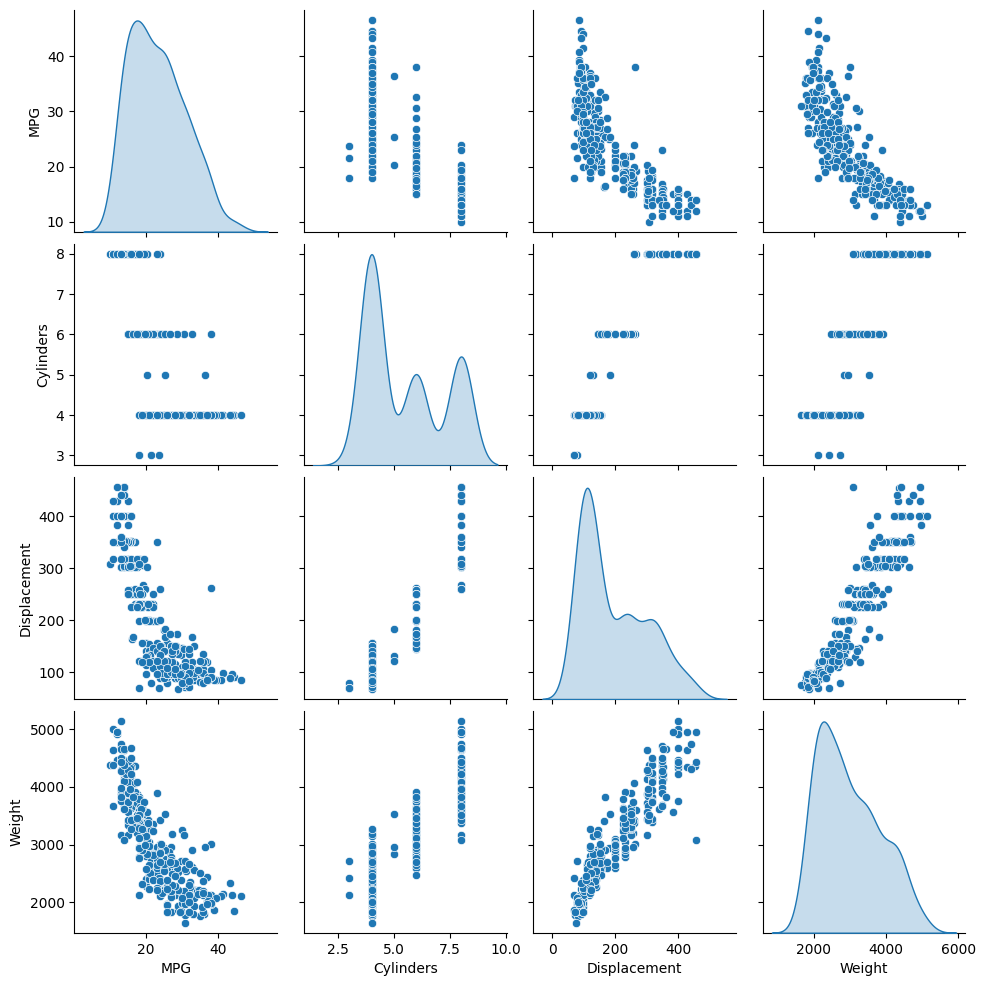
Controlliamo anche le statistiche generali. Nota come ciascuna funzione copre un intervallo molto diverso:
train_dataset.describe().transpose()
Separa le funzioni dalle etichette
Separare il valore target, l'"etichetta", dalle caratteristiche. Questa etichetta è il valore che addestrerai il modello per prevedere.
train_features = train_dataset.copy()
test_features = test_dataset.copy()
train_labels = train_features.pop('MPG')
test_labels = test_features.pop('MPG')
Normalizzazione
Nella tabella delle statistiche è facile vedere quanto sono diversi gli intervalli di ciascuna caratteristica:
train_dataset.describe().transpose()[['mean', 'std']]
È buona norma normalizzare le funzioni che utilizzano scale e intervalli diversi.
Uno dei motivi per cui questo è importante è perché le caratteristiche vengono moltiplicate per i pesi del modello. Quindi, la scala delle uscite e la scala dei gradienti sono influenzate dalla scala degli ingressi.
Sebbene un modello possa convergere senza la normalizzazione delle caratteristiche, la normalizzazione rende l'addestramento molto più stabile.
Il livello di normalizzazione
tf.keras.layers.Normalization è un modo semplice e pulito per aggiungere la normalizzazione delle funzionalità al tuo modello.
Il primo passo è creare il livello:
normalizer = tf.keras.layers.Normalization(axis=-1)
Quindi, adatta lo stato del livello di preelaborazione ai dati chiamando Normalization.adapt :
normalizer.adapt(np.array(train_features))
Calcola la media e la varianza e memorizzale nel livello:
print(normalizer.mean.numpy())
[[ 5.478 195.318 104.869 2990.252 15.559 75.898 0.178 0.197
0.624]]
Quando il livello viene chiamato, restituisce i dati di input, con ciascuna funzione normalizzata in modo indipendente:
first = np.array(train_features[:1])
with np.printoptions(precision=2, suppress=True):
print('First example:', first)
print()
print('Normalized:', normalizer(first).numpy())
First example: [[ 4. 90. 75. 2125. 14.5 74. 0. 0. 1. ]] Normalized: [[-0.87 -1.01 -0.79 -1.03 -0.38 -0.52 -0.47 -0.5 0.78]]
Regressione lineare
Prima di costruire un modello di rete neurale profonda, inizia con la regressione lineare utilizzando una e più variabili.
Regressione lineare con una variabile
Inizia con una regressione lineare a variabile singola per prevedere 'MPG' da 'Horsepower' .
L'addestramento di un modello con tf.keras in genere inizia definendo l'architettura del modello. Utilizzare un modello tf.keras.Sequential , che rappresenta una sequenza di passaggi .
Ci sono due passaggi nel tuo modello di regressione lineare a variabile singola:
- Normalizza le funzioni di input
'Horsepower'usando il livello di preelaborazionetf.keras.layers.Normalization. - Applicare una trasformazione lineare (\(y = mx+b\)) per produrre 1 output utilizzando un livello lineare (
tf.keras.layers.Dense).
Il numero di input può essere impostato dall'argomento input_shape o automaticamente quando il modello viene eseguito per la prima volta.
Innanzitutto, crea un array NumPy composto dalle funzionalità 'Horsepower' . Quindi, istanziare tf.keras.layers.Normalization e adattare il suo stato ai dati di horsepower :
horsepower = np.array(train_features['Horsepower'])
horsepower_normalizer = layers.Normalization(input_shape=[1,], axis=None)
horsepower_normalizer.adapt(horsepower)
Costruisci il modello Keras Sequential:
horsepower_model = tf.keras.Sequential([
horsepower_normalizer,
layers.Dense(units=1)
])
horsepower_model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense (Dense) (None, 1) 2
=================================================================
Total params: 5
Trainable params: 2
Non-trainable params: 3
_________________________________________________________________
Questo modello prevederà 'MPG' da 'Horsepower' .
Esegui il modello non addestrato sui primi 10 valori "Potenza". L'output non sarà buono, ma nota che ha la forma prevista di (10, 1) :
horsepower_model.predict(horsepower[:10])
array([[-1.186],
[-0.67 ],
[ 2.189],
[-1.662],
[-1.504],
[-0.59 ],
[-1.782],
[-1.504],
[-0.392],
[-0.67 ]], dtype=float32)
Una volta creato il modello, configurare la procedura di addestramento utilizzando il metodo Keras Model.compile . Gli argomenti più importanti da compilare sono la loss e l' optimizer , poiché questi definiscono cosa verrà ottimizzato ( mean_absolute_error ) e come (usando tf.keras.optimizers.Adam ).
horsepower_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
Usa Keras Model.fit per eseguire l'allenamento per 100 epoche:
%%time
history = horsepower_model.fit(
train_features['Horsepower'],
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.79 s, sys: 797 ms, total: 5.59 s Wall time: 3.8 s
Visualizza l'avanzamento dell'allenamento del modello utilizzando le statistiche memorizzate nell'oggetto history :
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_loss(history):
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.ylim([0, 10])
plt.xlabel('Epoch')
plt.ylabel('Error [MPG]')
plt.legend()
plt.grid(True)
plot_loss(history)
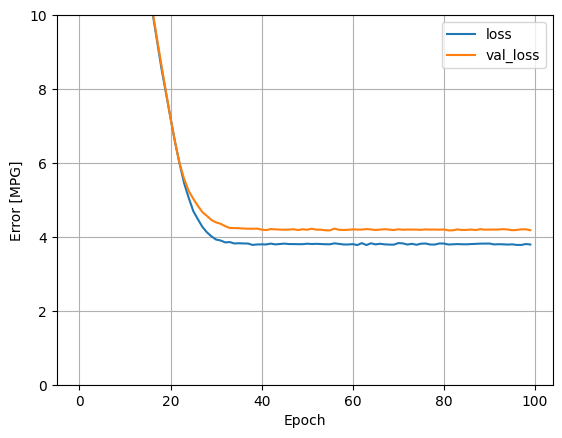
Raccogli i risultati sul set di test per dopo:
test_results = {}
test_results['horsepower_model'] = horsepower_model.evaluate(
test_features['Horsepower'],
test_labels, verbose=0)
Poiché si tratta di una regressione a variabile singola, è facile visualizzare le previsioni del modello in funzione dell'input:
x = tf.linspace(0.0, 250, 251)
y = horsepower_model.predict(x)
def plot_horsepower(x, y):
plt.scatter(train_features['Horsepower'], train_labels, label='Data')
plt.plot(x, y, color='k', label='Predictions')
plt.xlabel('Horsepower')
plt.ylabel('MPG')
plt.legend()
plot_horsepower(x, y)
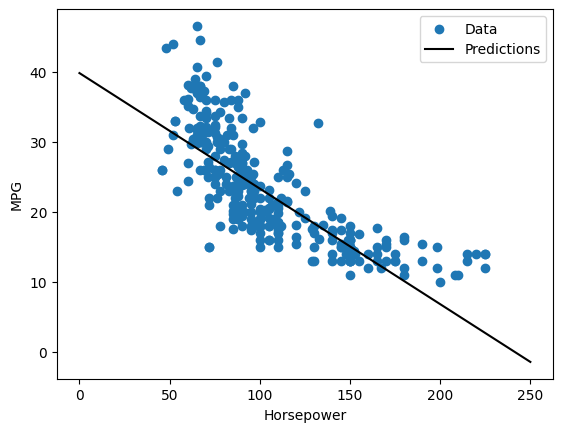
Regressione lineare con input multipli
Puoi utilizzare una configurazione quasi identica per fare previsioni basate su più input. Questo modello fa ancora lo stesso \(y = mx+b\) tranne che \(m\) è una matrice e \(b\) è un vettore.
Crea nuovamente un modello Keras Sequential in due passaggi con il primo livello normalizer ( tf.keras.layers.Normalization(axis=-1) ) che hai definito in precedenza e adattato all'intero set di dati:
linear_model = tf.keras.Sequential([
normalizer,
layers.Dense(units=1)
])
Quando chiami Model.predict su un batch di input, produce units=1 output per ogni esempio:
linear_model.predict(train_features[:10])
array([[ 0.441],
[ 1.522],
[ 0.188],
[ 1.169],
[ 0.058],
[ 0.965],
[ 0.034],
[-0.674],
[ 0.437],
[-0.37 ]], dtype=float32)
Quando chiami il modello, verranno create le sue matrici di peso: controlla che i pesi del kernel ( \(m\) in \(y=mx+b\)) abbiano una forma di (9, 1) :
linear_model.layers[1].kernel
<tf.Variable 'dense_1/kernel:0' shape=(9, 1) dtype=float32, numpy=
array([[-0.702],
[ 0.307],
[ 0.114],
[ 0.233],
[ 0.244],
[ 0.322],
[-0.725],
[-0.151],
[ 0.407]], dtype=float32)>
Configura il modello con Keras Model.compile e addestra con Model.fit per 100 epoche:
linear_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
%%time
history = linear_model.fit(
train_features,
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.89 s, sys: 740 ms, total: 5.63 s Wall time: 3.75 s
L'utilizzo di tutti gli input in questo modello di regressione consente di ottenere un errore di addestramento e convalida molto inferiore rispetto a horsepower_model , che aveva un input:
plot_loss(history)
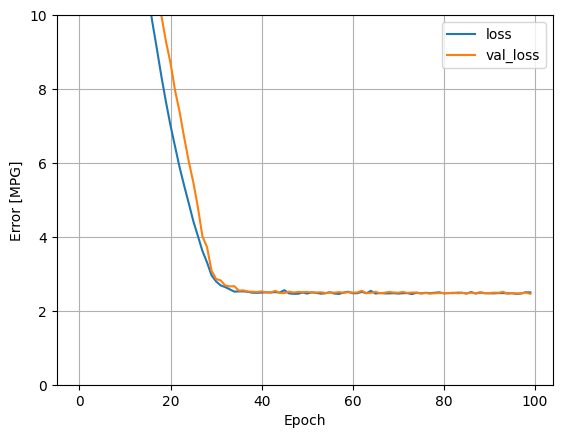
Raccogli i risultati sul set di test per dopo:
test_results['linear_model'] = linear_model.evaluate(
test_features, test_labels, verbose=0)
Regressione con una rete neurale profonda (DNN)
Nella sezione precedente sono stati implementati due modelli lineari per ingressi singoli e multipli.
Qui implementerai modelli DNN a input singolo e multiplo.
Il codice è sostanzialmente lo stesso, tranne per il fatto che il modello viene ampliato per includere alcuni livelli non lineari "nascosti". Il nome "nascosto" qui significa semplicemente non collegato direttamente agli ingressi o alle uscite.
Questi modelli conterranno alcuni livelli in più rispetto al modello lineare:
- Il livello di normalizzazione, come prima (con
horsepower_normalizerper un modello a input singolo enormalizerper un modello a input multipli). - Due strati nascosti, non lineari,
Densecon la non linearità della funzione di attivazionerelu( relu ). - Uno strato a output singolo
Denselineare.
Entrambi i modelli utilizzeranno la stessa procedura di addestramento, quindi il metodo compile è incluso nella funzione build_and_compile_model di seguito.
def build_and_compile_model(norm):
model = keras.Sequential([
norm,
layers.Dense(64, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
model.compile(loss='mean_absolute_error',
optimizer=tf.keras.optimizers.Adam(0.001))
return model
Regressione utilizzando un DNN e un singolo input
Crea un modello DNN con solo 'Horsepower' come input e horsepower_normalizer (definito in precedenza) come livello di normalizzazione:
dnn_horsepower_model = build_and_compile_model(horsepower_normalizer)
Questo modello ha alcuni parametri più addestrabili rispetto ai modelli lineari:
dnn_horsepower_model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense_2 (Dense) (None, 64) 128
dense_3 (Dense) (None, 64) 4160
dense_4 (Dense) (None, 1) 65
=================================================================
Total params: 4,356
Trainable params: 4,353
Non-trainable params: 3
_________________________________________________________________
Allena il modello con Keras Model.fit :
%%time
history = dnn_horsepower_model.fit(
train_features['Horsepower'],
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.07 s, sys: 691 ms, total: 5.76 s Wall time: 3.92 s
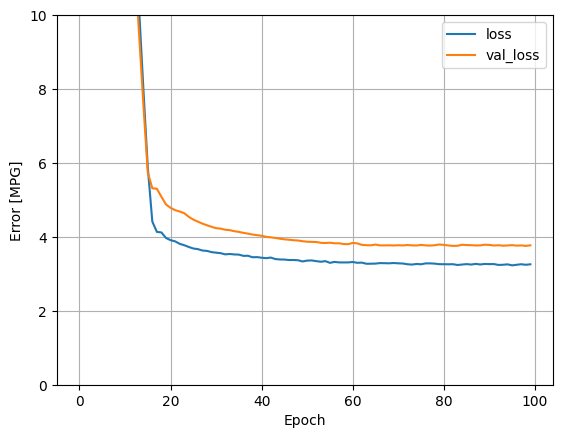
Questo modello ha prestazioni leggermente migliori rispetto al modello lineare a ingresso singolo horsepower_model :
plot_loss(history)
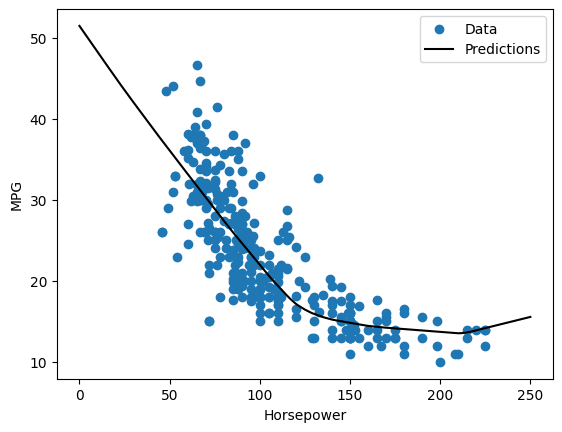
Se tracciate le previsioni in funzione di 'Horsepower' , dovreste notare come questo modello sfrutti la non linearità fornita dai livelli nascosti:
x = tf.linspace(0.0, 250, 251)
y = dnn_horsepower_model.predict(x)
plot_horsepower(x, y)
Raccogli i risultati sul set di test per dopo:
test_results['dnn_horsepower_model'] = dnn_horsepower_model.evaluate(
test_features['Horsepower'], test_labels,
verbose=0)
Regressione utilizzando un DNN e input multipli
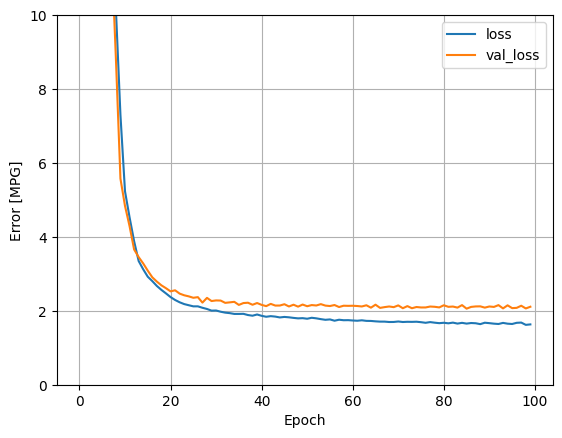
Ripetere il processo precedente utilizzando tutti gli input. Le prestazioni del modello migliorano leggermente sul set di dati di convalida.
dnn_model = build_and_compile_model(normalizer)
dnn_model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization (Normalizatio (None, 9) 19
n)
dense_5 (Dense) (None, 64) 640
dense_6 (Dense) (None, 64) 4160
dense_7 (Dense) (None, 1) 65
=================================================================
Total params: 4,884
Trainable params: 4,865
Non-trainable params: 19
_________________________________________________________________
%%time
history = dnn_model.fit(
train_features,
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.08 s, sys: 725 ms, total: 5.8 s Wall time: 3.94 s
plot_loss(history)
Raccogli i risultati sul set di prova:
test_results['dnn_model'] = dnn_model.evaluate(test_features, test_labels, verbose=0)
Prestazione
Poiché tutti i modelli sono stati addestrati, puoi rivedere le prestazioni del loro set di test:
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
Questi risultati corrispondono all'errore di convalida osservato durante l'addestramento.
Fare previsioni
Ora puoi fare previsioni con dnn_model sul set di test utilizzando Keras Model.predict e rivedere la perdita:
test_predictions = dnn_model.predict(test_features).flatten()
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
lims = [0, 50]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)

Sembra che il modello preveda ragionevolmente bene.
Ora, controlla la distribuzione degli errori:
error = test_predictions - test_labels
plt.hist(error, bins=25)
plt.xlabel('Prediction Error [MPG]')
_ = plt.ylabel('Count')

Se sei soddisfatto del modello, salvalo per un uso successivo con Model.save :
dnn_model.save('dnn_model')
2022-01-26 07:26:13.372245: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: dnn_model/assets
Se ricarichi il modello, fornisce un output identico:
reloaded = tf.keras.models.load_model('dnn_model')
test_results['reloaded'] = reloaded.evaluate(
test_features, test_labels, verbose=0)
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
Conclusione
Questo quaderno ha introdotto alcune tecniche per gestire un problema di regressione. Ecco alcuni altri suggerimenti che possono aiutare:
- L'errore quadratico medio (MSE) (
tf.losses.MeanSquaredError) e l'errore medio assoluto (MAE) (tf.losses.MeanAbsoluteError) sono funzioni di perdita comuni utilizzate per problemi di regressione. MAE è meno sensibile ai valori anomali. Diverse funzioni di perdita vengono utilizzate per problemi di classificazione. - Allo stesso modo, le metriche di valutazione utilizzate per la regressione differiscono dalla classificazione.
- Quando le funzioni dei dati di input numerici hanno valori con intervalli diversi, ciascuna funzione deve essere ridimensionata in modo indipendente allo stesso intervallo.
- L'overfitting è un problema comune per i modelli DNN, anche se non è stato un problema per questo tutorial. Visita il tutorial Overfit e underfit per ulteriore aiuto con questo.
# MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
