 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запустить в Google Colab Запустить в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
В этом руководстве показано, как классифицировать сильно несбалансированный набор данных, в котором количество примеров в одном классе значительно превышает количество примеров в другом. Вы будете работать с набором данных обнаружения мошенничества с кредитными картами , размещенным на Kaggle. Цель состоит в том, чтобы обнаружить всего 492 мошеннических транзакции из 284 807 транзакций в целом. Вы будете использовать Keras для определения веса модели и класса , чтобы помочь модели учиться на несбалансированных данных. .
Этот учебник содержит полный код для:
- Загрузите файл CSV с помощью Pandas.
- Создавайте обучающие, проверочные и тестовые наборы.
- Определите и обучите модель с помощью Keras (включая настройку весов классов).
- Оцените модель, используя различные показатели (включая точность и полноту).
- Попробуйте общие методы работы с несбалансированными данными, такие как:
- Взвешивание классов
- Передискретизация
Настраивать
import tensorflow as tf
from tensorflow import keras
import os
import tempfile
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
Обработка и исследование данных
Загрузите набор данных Kaggle о мошенничестве с кредитными картами
Pandas — это библиотека Python с множеством полезных утилит для загрузки и работы со структурированными данными. Его можно использовать для загрузки CSV в Pandas DataFrame .
file = tf.keras.utils
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()
raw_df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe()
Изучите дисбаланс ярлыков классов
Давайте посмотрим на дисбаланс набора данных:
neg, pos = np.bincount(raw_df['Class'])
total = neg + pos
print('Examples:\n Total: {}\n Positive: {} ({:.2f}% of total)\n'.format(
total, pos, 100 * pos / total))
Examples:
Total: 284807
Positive: 492 (0.17% of total)
Это показывает небольшую долю положительных образцов.
Очистить, разделить и нормализовать данные
Необработанные данные имеют несколько проблем. Во-первых, столбцы Time и Amount слишком переменны, чтобы их можно было использовать напрямую. Отбросьте столбец « Time » (поскольку непонятно, что он означает) и возьмите лог столбца « Amount », чтобы уменьшить его диапазон.
cleaned_df = raw_df.copy()
# You don't want the `Time` column.
cleaned_df.pop('Time')
# The `Amount` column covers a huge range. Convert to log-space.
eps = 0.001 # 0 => 0.1¢
cleaned_df['Log Ammount'] = np.log(cleaned_df.pop('Amount')+eps)
Разделите набор данных на обучающие, проверочные и тестовые наборы. Набор проверки используется во время подбора модели для оценки потерь и любых показателей, однако модель не соответствует этим данным. Набор тестов полностью не используется на этапе обучения и используется только в конце, чтобы оценить, насколько хорошо модель обобщает новые данные. Это особенно важно для несбалансированных наборов данных, где переобучение вызывает серьезную озабоченность из-за отсутствия обучающих данных.
# Use a utility from sklearn to split and shuffle your dataset.
train_df, test_df = train_test_split(cleaned_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)
# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
bool_train_labels = train_labels != 0
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))
train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)
Нормализуйте входные функции с помощью sklearn StandardScaler. Это установит среднее значение в 0 и стандартное отклонение в 1.
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)
train_features = np.clip(train_features, -5, 5)
val_features = np.clip(val_features, -5, 5)
test_features = np.clip(test_features, -5, 5)
print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)
print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)
Training labels shape: (182276,) Validation labels shape: (45569,) Test labels shape: (56962,) Training features shape: (182276, 29) Validation features shape: (45569, 29) Test features shape: (56962, 29)
Посмотрите на распределение данных
Затем сравните распределения положительных и отрицательных примеров по нескольким функциям. Хорошие вопросы, которые следует задать себе в этот момент:
- Есть ли смысл в этих раздачах?
- да. Вы нормализовали ввод, и они в основном сосредоточены в диапазоне
+/- 2.
- да. Вы нормализовали ввод, и они в основном сосредоточены в диапазоне
- Вы видите разницу между дистрибутивами?
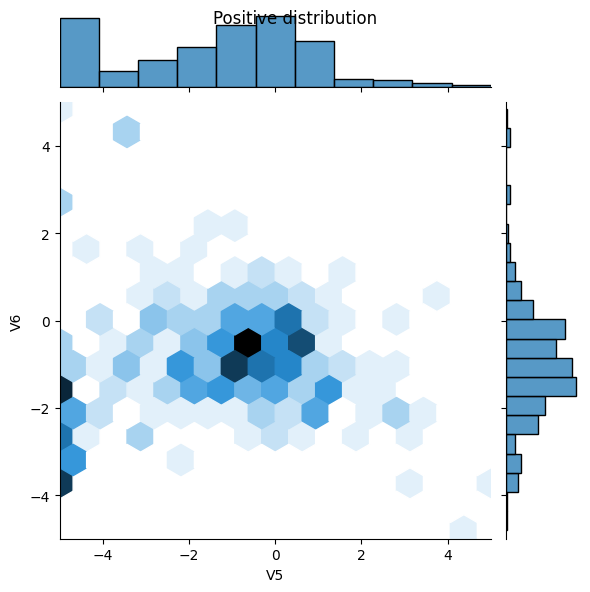
- Да, положительные примеры содержат гораздо более высокий уровень экстремальных значений.
pos_df = pd.DataFrame(train_features[ bool_train_labels], columns=train_df.columns)
neg_df = pd.DataFrame(train_features[~bool_train_labels], columns=train_df.columns)
sns.jointplot(x=pos_df['V5'], y=pos_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
plt.suptitle("Positive distribution")
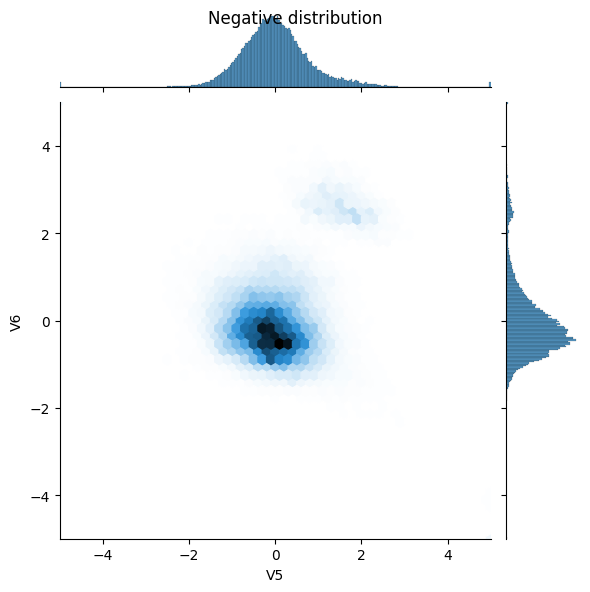
sns.jointplot(x=neg_df['V5'], y=neg_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
_ = plt.suptitle("Negative distribution")
Определение модели и показателей
Определите функцию, которая создает простую нейронную сеть с плотно связанным скрытым слоем, отсевающим слоем для уменьшения переобучения и выходным сигмовидным слоем, который возвращает вероятность мошеннической транзакции:
METRICS = [
keras.metrics.TruePositives(name='tp'),
keras.metrics.FalsePositives(name='fp'),
keras.metrics.TrueNegatives(name='tn'),
keras.metrics.FalseNegatives(name='fn'),
keras.metrics.BinaryAccuracy(name='accuracy'),
keras.metrics.Precision(name='precision'),
keras.metrics.Recall(name='recall'),
keras.metrics.AUC(name='auc'),
keras.metrics.AUC(name='prc', curve='PR'), # precision-recall curve
]
def make_model(metrics=METRICS, output_bias=None):
if output_bias is not None:
output_bias = tf.keras.initializers.Constant(output_bias)
model = keras.Sequential([
keras.layers.Dense(
16, activation='relu',
input_shape=(train_features.shape[-1],)),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid',
bias_initializer=output_bias),
])
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.BinaryCrossentropy(),
metrics=metrics)
return model
Понимание полезных показателей
Обратите внимание, что есть несколько метрик, определенных выше, которые могут быть вычислены моделью, которые будут полезны при оценке производительности.
- Ложноотрицательные и ложноположительные результаты — это образцы, которые были неправильно классифицированы.
- Истинные отрицательные и истинные положительные результаты — это образцы, которые были правильно классифицированы.
- Точность — это процент правильно классифицированных примеров > \(\frac{\text{true samples} }{\text{total samples} }\)
- Точность — это процент прогнозируемых положительных результатов, которые были правильно классифицированы > \(\frac{\text{true positives} }{\text{true positives + false positives} }\)
- Отзыв — это процент фактических положительных результатов, которые были правильно классифицированы > \(\frac{\text{true positives} }{\text{true positives + false negatives} }\)
- AUC относится к площади под кривой рабочей характеристики приемника (ROC-AUC). Этот показатель равен вероятности того, что классификатор ранжирует случайную положительную выборку выше, чем случайную отрицательную выборку.
- AUPRC относится к площади под кривой кривой точности-отзыва. Эта метрика вычисляет пары точность-отзыв для различных порогов вероятности.
Читать далее:
- Правда против Ложь и Положительный против Отрицательный
- Точность
- Точность и отзыв
- ОКР-АУК
- Взаимосвязь между Precision-Recall и кривыми ROC
Базовая модель
Построить модель
Теперь создайте и обучите свою модель, используя функцию, которая была определена ранее. Обратите внимание, что модель подходит для использования большего размера партии, чем по умолчанию, равного 2048, это важно для обеспечения того, чтобы каждая партия имела достойный шанс содержать несколько положительных образцов. Если бы размер пакета был слишком маленьким, у них, вероятно, не было бы мошеннических транзакций, на которых можно было бы учиться.
EPOCHS = 100
BATCH_SIZE = 2048
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_prc',
verbose=1,
patience=10,
mode='max',
restore_best_weights=True)
model = make_model()
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 16) 480
dropout (Dropout) (None, 16) 0
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 497
Trainable params: 497
Non-trainable params: 0
_________________________________________________________________
Тестовый запуск модели:
model.predict(train_features[:10])
array([[0.9466284 ],
[0.7211031 ],
[0.60527885],
[0.8335568 ],
[0.5909625 ],
[0.6751574 ],
[0.6623665 ],
[0.81066036],
[0.50712407],
[0.8296292 ]], dtype=float32)
Необязательно: Установите правильное начальное смещение.
Эти первоначальные догадки не велики. Вы знаете, что набор данных несбалансирован. Установите смещение выходного слоя, чтобы отразить это (см. Рецепт для обучения нейронных сетей: «инициализируйте хорошо» ). Это может помочь с начальной конвергенцией.
При инициализации смещения по умолчанию потери должны составлять около math.log(2) = 0.69314
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 1.2781
Правильное смещение для установки может быть получено из:
\[ p_0 = pos/(pos + neg) = 1/(1+e^{-b_0}) \]
\[ b_0 = -log_e(1/p_0 - 1) \]
\[ b_0 = log_e(pos/neg)\]
initial_bias = np.log([pos/neg])
initial_bias
array([-6.35935934])
Установите это как начальное смещение, и модель будет давать гораздо более разумные начальные предположения.
Должно быть около: pos/total = 0.0018
model = make_model(output_bias=initial_bias)
model.predict(train_features[:10])
array([[2.3598122e-05],
[1.5476024e-03],
[6.8338902e-04],
[9.4873342e-04],
[1.0742771e-03],
[7.7475846e-04],
[1.2199467e-03],
[5.5399281e-04],
[1.6213538e-03],
[3.0470363e-04]], dtype=float32)
При такой инициализации первоначальные потери должны быть примерно равны:
\[-p_0log(p_0)-(1-p_0)log(1-p_0) = 0.01317\]
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 0.0200
Эти первоначальные потери примерно в 50 раз меньше, чем если бы они были с наивной инициализацией.
Таким образом, модели не нужно тратить первые несколько эпох только на то, чтобы понять, что положительные примеры маловероятны. Это также облегчает чтение графиков потерь во время обучения.
Контрольные точки начальных весов
Чтобы сделать различные тренировочные прогоны более сопоставимыми, сохраните веса исходной модели в файле контрольных точек и загрузите их в каждую модель перед тренировкой:
initial_weights = os.path.join(tempfile.mkdtemp(), 'initial_weights')
model.save_weights(initial_weights)
Убедитесь, что исправление смещения помогает
Прежде чем двигаться дальше, быстро подтвердите, что тщательная инициализация смещения действительно помогла.
Обучите модель в течение 20 эпох, с этой тщательной инициализацией и без нее, и сравните потери:
model = make_model()
model.load_weights(initial_weights)
model.layers[-1].bias.assign([0.0])
zero_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
model = make_model()
model.load_weights(initial_weights)
careful_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
def plot_loss(history, label, n):
# Use a log scale on y-axis to show the wide range of values.
plt.semilogy(history.epoch, history.history['loss'],
color=colors[n], label='Train ' + label)
plt.semilogy(history.epoch, history.history['val_loss'],
color=colors[n], label='Val ' + label,
linestyle="--")
plt.xlabel('Epoch')
plt.ylabel('Loss')
plot_loss(zero_bias_history, "Zero Bias", 0)
plot_loss(careful_bias_history, "Careful Bias", 1)
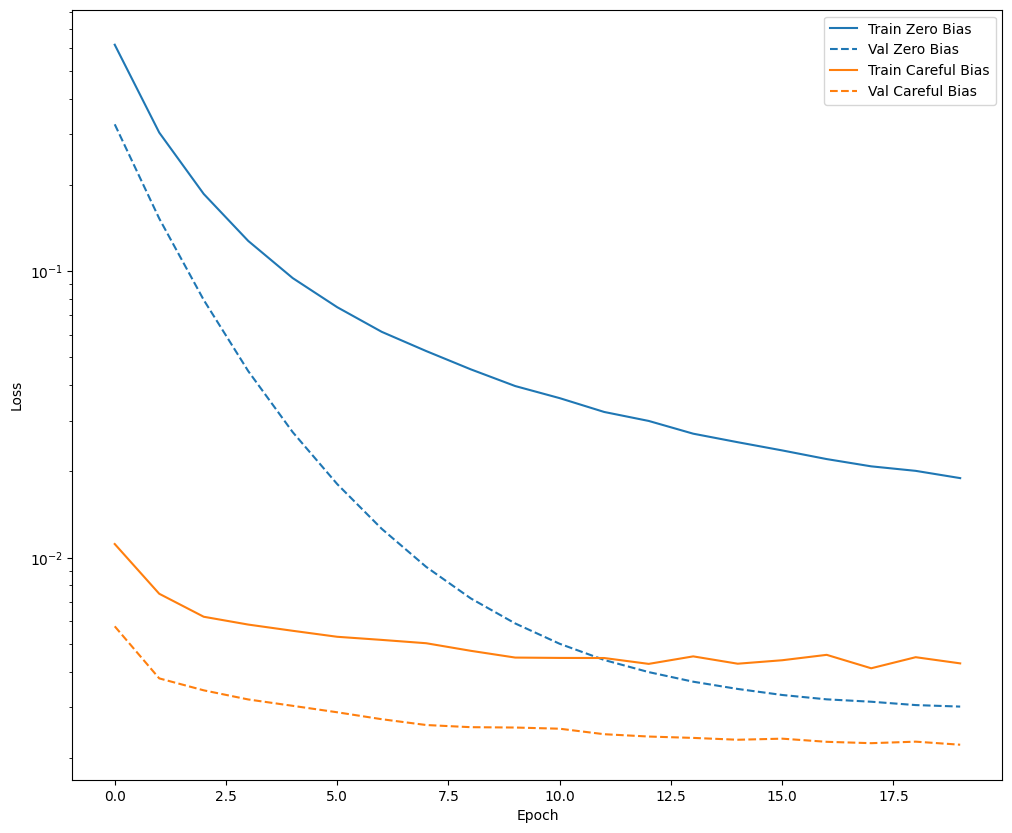
На приведенном выше рисунке ясно показано: с точки зрения потерь при проверке в этой проблеме эта тщательная инициализация дает явное преимущество.
Обучите модель
model = make_model()
model.load_weights(initial_weights)
baseline_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels))
Epoch 1/100 90/90 [==============================] - 3s 15ms/step - loss: 0.0161 - tp: 64.0000 - fp: 9.0000 - tn: 227425.0000 - fn: 347.0000 - accuracy: 0.9984 - precision: 0.8767 - recall: 0.1557 - auc: 0.6148 - prc: 0.1692 - val_loss: 0.0115 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7205 - val_prc: 0.2571 Epoch 2/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0087 - tp: 49.0000 - fp: 11.0000 - tn: 181940.0000 - fn: 276.0000 - accuracy: 0.9984 - precision: 0.8167 - recall: 0.1508 - auc: 0.8085 - prc: 0.3735 - val_loss: 0.0054 - val_tp: 35.0000 - val_fp: 6.0000 - val_tn: 45477.0000 - val_fn: 51.0000 - val_accuracy: 0.9987 - val_precision: 0.8537 - val_recall: 0.4070 - val_auc: 0.9065 - val_prc: 0.6598 Epoch 3/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0061 - tp: 126.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 199.0000 - accuracy: 0.9988 - precision: 0.8235 - recall: 0.3877 - auc: 0.8997 - prc: 0.6187 - val_loss: 0.0046 - val_tp: 55.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 31.0000 - val_accuracy: 0.9991 - val_precision: 0.8730 - val_recall: 0.6395 - val_auc: 0.9063 - val_prc: 0.6941 Epoch 4/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 172.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 153.0000 - accuracy: 0.9990 - precision: 0.8473 - recall: 0.5292 - auc: 0.9068 - prc: 0.6448 - val_loss: 0.0044 - val_tp: 58.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 28.0000 - val_accuracy: 0.9992 - val_precision: 0.8788 - val_recall: 0.6744 - val_auc: 0.9064 - val_prc: 0.7114 Epoch 5/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 167.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 158.0000 - accuracy: 0.9990 - precision: 0.8477 - recall: 0.5138 - auc: 0.9134 - prc: 0.6215 - val_loss: 0.0043 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7181 Epoch 6/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 193.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 132.0000 - accuracy: 0.9991 - precision: 0.8733 - recall: 0.5938 - auc: 0.9198 - prc: 0.6760 - val_loss: 0.0042 - val_tp: 59.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 27.0000 - val_accuracy: 0.9992 - val_precision: 0.8806 - val_recall: 0.6860 - val_auc: 0.9064 - val_prc: 0.7370 Epoch 7/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 183.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 142.0000 - accuracy: 0.9991 - precision: 0.8592 - recall: 0.5631 - auc: 0.9202 - prc: 0.6737 - val_loss: 0.0042 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7463 Epoch 8/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 171.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 154.0000 - accuracy: 0.9990 - precision: 0.8465 - recall: 0.5262 - auc: 0.9156 - prc: 0.6574 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7480 Epoch 9/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 196.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8711 - recall: 0.6031 - auc: 0.9218 - prc: 0.6799 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7550 Epoch 10/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 173.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 152.0000 - accuracy: 0.9990 - precision: 0.8650 - recall: 0.5323 - auc: 0.9048 - prc: 0.6520 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9122 - val_prc: 0.7598 Epoch 11/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 190.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8597 - recall: 0.5846 - auc: 0.9172 - prc: 0.6779 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9065 - val_prc: 0.7595 Epoch 12/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 192.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 133.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.5908 - auc: 0.9281 - prc: 0.7312 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9123 - val_prc: 0.7648 Epoch 13/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 185.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 140.0000 - accuracy: 0.9991 - precision: 0.8565 - recall: 0.5692 - auc: 0.9328 - prc: 0.7222 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7615 Epoch 14/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 183.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 142.0000 - accuracy: 0.9990 - precision: 0.8472 - recall: 0.5631 - auc: 0.9295 - prc: 0.6770 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7670 Epoch 15/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 194.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8700 - recall: 0.5969 - auc: 0.9344 - prc: 0.7233 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7672 Epoch 16/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 207.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8697 - recall: 0.6369 - auc: 0.9329 - prc: 0.7194 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7694 Epoch 17/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 190.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8716 - recall: 0.5846 - auc: 0.9345 - prc: 0.7265 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7705 Epoch 18/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8622 - recall: 0.5969 - auc: 0.9344 - prc: 0.7199 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7725 Epoch 19/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 205.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8613 - recall: 0.6308 - auc: 0.9346 - prc: 0.7266 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7739 Epoch 20/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 207.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8809 - recall: 0.6369 - auc: 0.9421 - prc: 0.7634 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7729 Epoch 21/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0040 - tp: 204.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8644 - recall: 0.6277 - auc: 0.9360 - prc: 0.7340 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7756 Epoch 22/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 207.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8884 - recall: 0.6369 - auc: 0.9328 - prc: 0.7277 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7773 Epoch 23/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0041 - tp: 191.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8527 - recall: 0.5877 - auc: 0.9375 - prc: 0.7280 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8857 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7790 Epoch 24/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 196.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6031 - auc: 0.9375 - prc: 0.7466 - val_loss: 0.0038 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7762 Epoch 25/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 204.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8681 - recall: 0.6277 - auc: 0.9467 - prc: 0.7480 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9123 - val_prc: 0.7789 Epoch 26/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8661 - recall: 0.5969 - auc: 0.9360 - prc: 0.7292 - val_loss: 0.0038 - val_tp: 60.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8955 - val_recall: 0.6977 - val_auc: 0.9123 - val_prc: 0.7783 Epoch 27/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8776 - recall: 0.6400 - auc: 0.9376 - prc: 0.7632 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7772 Epoch 28/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 202.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 123.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6215 - auc: 0.9408 - prc: 0.7638 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7808 Epoch 29/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 214.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8807 - recall: 0.6585 - auc: 0.9347 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7806 Epoch 30/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 197.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 128.0000 - accuracy: 0.9991 - precision: 0.8640 - recall: 0.6062 - auc: 0.9346 - prc: 0.7489 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7804 Epoch 31/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 213.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 112.0000 - accuracy: 0.9992 - precision: 0.8659 - recall: 0.6554 - auc: 0.9407 - prc: 0.7615 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7809 Epoch 32/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9407 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7821 Epoch 33/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 210.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 115.0000 - accuracy: 0.9992 - precision: 0.8787 - recall: 0.6462 - auc: 0.9392 - prc: 0.7642 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7826 Epoch 34/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9423 - prc: 0.7759 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7830 Epoch 35/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 35.0000 - tn: 181916.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8566 - recall: 0.6431 - auc: 0.9407 - prc: 0.7381 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836 Epoch 36/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 204.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8831 - recall: 0.6277 - auc: 0.9407 - prc: 0.7587 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840 Epoch 37/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8672 - recall: 0.6431 - auc: 0.9345 - prc: 0.7386 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7849 Epoch 38/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 198.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.6092 - auc: 0.9454 - prc: 0.7488 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7844 Epoch 39/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 209.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8782 - recall: 0.6431 - auc: 0.9407 - prc: 0.7419 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840 Epoch 40/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 198.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8761 - recall: 0.6092 - auc: 0.9546 - prc: 0.7644 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7835 Epoch 41/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8745 - recall: 0.6431 - auc: 0.9377 - prc: 0.7587 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7827 Epoch 42/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 195.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8667 - recall: 0.6000 - auc: 0.9345 - prc: 0.7436 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7834 Epoch 43/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8655 - recall: 0.6338 - auc: 0.9500 - prc: 0.7699 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836 Epoch 44/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8927 - recall: 0.6400 - auc: 0.9438 - prc: 0.7625 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7841 Epoch 45/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 205.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8686 - recall: 0.6308 - auc: 0.9422 - prc: 0.7519 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7847 Epoch 46/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 206.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8766 - recall: 0.6338 - auc: 0.9423 - prc: 0.7529 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7843 Epoch 47/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 219.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8866 - recall: 0.6738 - auc: 0.9377 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7871 Epoch 48/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8729 - recall: 0.6338 - auc: 0.9393 - prc: 0.7676 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7854 Epoch 49/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 215.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 110.0000 - accuracy: 0.9992 - precision: 0.8811 - recall: 0.6615 - auc: 0.9407 - prc: 0.7618 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9125 - val_prc: 0.7855 Epoch 50/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 214.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8699 - recall: 0.6585 - auc: 0.9377 - prc: 0.7727 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7858 Epoch 51/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 219.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8795 - recall: 0.6738 - auc: 0.9393 - prc: 0.7889 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7876 Epoch 52/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 217.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8967 - recall: 0.6677 - auc: 0.9439 - prc: 0.7812 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7887 Epoch 53/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 206.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8803 - recall: 0.6338 - auc: 0.9362 - prc: 0.7734 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7873 Epoch 54/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 223.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 102.0000 - accuracy: 0.9993 - precision: 0.8814 - recall: 0.6862 - auc: 0.9438 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7877 Epoch 55/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 220.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 105.0000 - accuracy: 0.9993 - precision: 0.8943 - recall: 0.6769 - auc: 0.9439 - prc: 0.7866 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886 Epoch 56/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 209.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8970 - recall: 0.6431 - auc: 0.9392 - prc: 0.7613 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886 Epoch 57/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0033 - tp: 221.0000 - fp: 23.0000 - tn: 181928.0000 - fn: 104.0000 - accuracy: 0.9993 - precision: 0.9057 - recall: 0.6800 - auc: 0.9516 - prc: 0.7954 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7873 Epoch 58/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8851 - recall: 0.6400 - auc: 0.9485 - prc: 0.7746 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7875 Epoch 59/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 216.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 109.0000 - accuracy: 0.9992 - precision: 0.8780 - recall: 0.6646 - auc: 0.9531 - prc: 0.7928 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7883 Epoch 60/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 211.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8719 - recall: 0.6492 - auc: 0.9469 - prc: 0.7808 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7882 Epoch 61/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 201.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 124.0000 - accuracy: 0.9992 - precision: 0.8933 - recall: 0.6185 - auc: 0.9424 - prc: 0.7720 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7881 Epoch 62/100 81/90 [==========================>...] - ETA: 0s - loss: 0.0034 - tp: 196.0000 - fp: 21.0000 - tn: 165565.0000 - fn: 106.0000 - accuracy: 0.9992 - precision: 0.9032 - recall: 0.6490 - auc: 0.9413 - prc: 0.7849Restoring model weights from the end of the best epoch: 52. 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 211.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8941 - recall: 0.6492 - auc: 0.9423 - prc: 0.7828 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7860 Epoch 62: early stopping
Проверить историю тренировок
В этом разделе вы создадите графики точности и потерь вашей модели на обучающем и проверочном наборе. Они полезны для проверки переоснащения, о чем вы можете узнать больше в учебнике Overfit and underfit .
Кроме того, вы можете создать эти графики для любой из метрик, которые вы создали выше. Ложноотрицательные результаты включены в качестве примера.
def plot_metrics(history):
metrics = ['loss', 'prc', 'precision', 'recall']
for n, metric in enumerate(metrics):
name = metric.replace("_"," ").capitalize()
plt.subplot(2,2,n+1)
plt.plot(history.epoch, history.history[metric], color=colors[0], label='Train')
plt.plot(history.epoch, history.history['val_'+metric],
color=colors[0], linestyle="--", label='Val')
plt.xlabel('Epoch')
plt.ylabel(name)
if metric == 'loss':
plt.ylim([0, plt.ylim()[1]])
elif metric == 'auc':
plt.ylim([0.8,1])
else:
plt.ylim([0,1])
plt.legend();
plot_metrics(baseline_history)
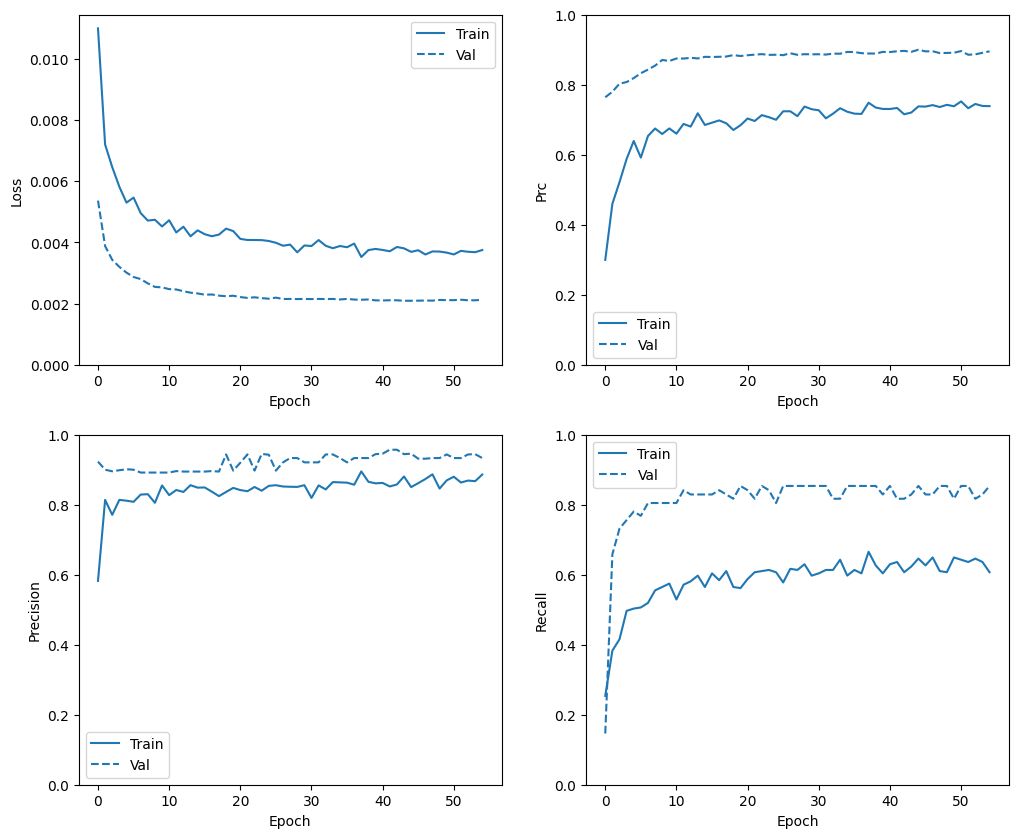
Оценить метрики
Вы можете использовать матрицу путаницы, чтобы суммировать фактические и предсказанные метки, где ось X — это предсказанная метка, а ось Y — фактическая метка:
train_predictions_baseline = model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_baseline = model.predict(test_features, batch_size=BATCH_SIZE)
def plot_cm(labels, predictions, p=0.5):
cm = confusion_matrix(labels, predictions > p)
plt.figure(figsize=(5,5))
sns.heatmap(cm, annot=True, fmt="d")
plt.title('Confusion matrix @{:.2f}'.format(p))
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
print('Total Fraudulent Transactions: ', np.sum(cm[1]))
Оцените свою модель в тестовом наборе данных и отобразите результаты для метрик, которые вы создали выше:
baseline_results = model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(model.metrics_names, baseline_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_baseline)
loss : 0.0024895435199141502 tp : 59.0 fp : 7.0 tn : 56874.0 fn : 22.0 accuracy : 0.9994909167289734 precision : 0.8939393758773804 recall : 0.7283950448036194 auc : 0.9318439960479736 prc : 0.8204483985900879 Legitimate Transactions Detected (True Negatives): 56874 Legitimate Transactions Incorrectly Detected (False Positives): 7 Fraudulent Transactions Missed (False Negatives): 22 Fraudulent Transactions Detected (True Positives): 59 Total Fraudulent Transactions: 81
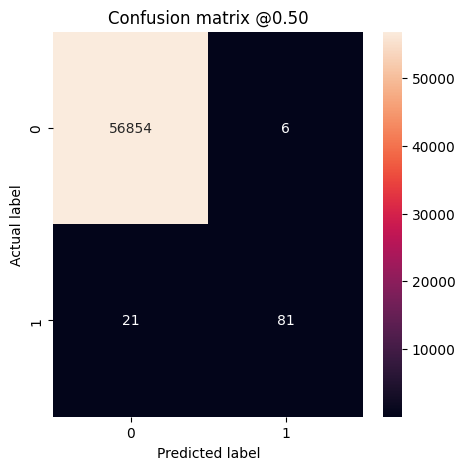
Если бы модель предсказывала все идеально, это была бы диагональная матрица, в которой значения вне главной диагонали, указывающие на неправильные предсказания, были бы равны нулю. В этом случае матрица показывает, что у вас относительно мало ложных срабатываний, а это означает, что было относительно немного законных транзакций, которые были неправильно помечены. Однако вы, вероятно, захотите иметь еще меньше ложноотрицательных результатов, несмотря на стоимость увеличения количества ложноположительных результатов. Этот компромисс может быть предпочтительнее, потому что ложные отрицательные результаты позволят пройти мошенническим транзакциям, тогда как ложные положительные результаты могут привести к тому, что клиенту будет отправлено электронное письмо с просьбой проверить активность своей карты.
Постройте ОКР
Теперь постройте ROC . Этот график полезен, потому что он сразу показывает диапазон производительности, которого может достичь модель, просто настроив выходной порог.
def plot_roc(name, labels, predictions, **kwargs):
fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)
plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
plt.xlabel('False positives [%]')
plt.ylabel('True positives [%]')
plt.xlim([-0.5,20])
plt.ylim([80,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
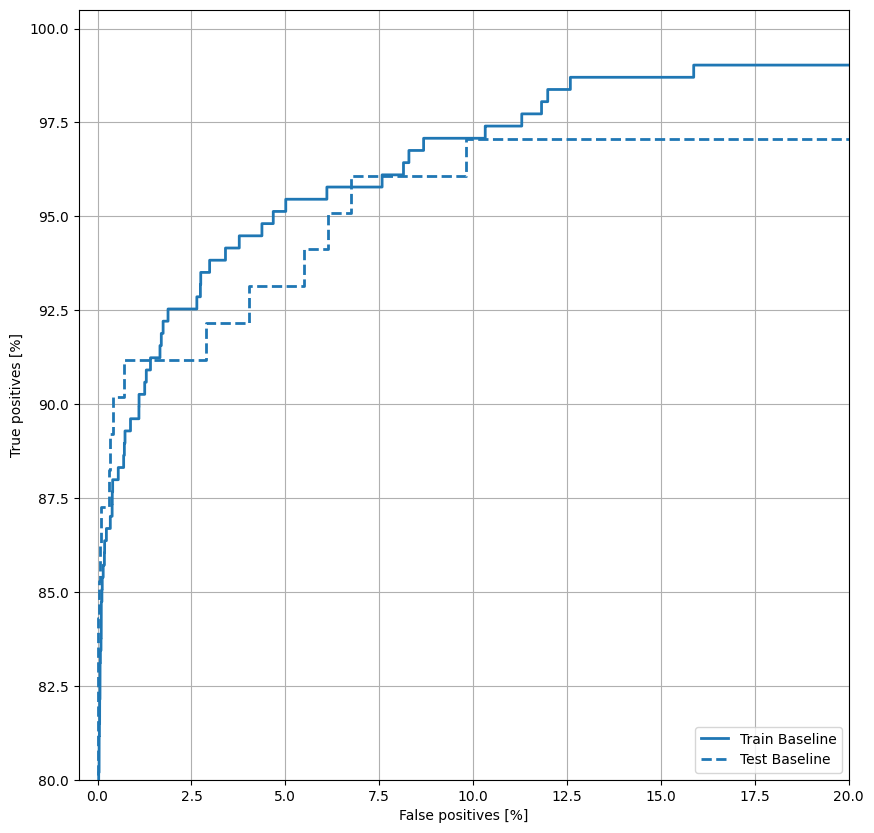
Постройте AUPRC
Теперь постройте AUPRC . Площадь под интерполированной кривой точности-отзыва, полученной нанесением точек (отзыва, точности) для различных значений порога классификации. В зависимости от того, как он рассчитывается, PR AUC может быть эквивалентен средней точности модели.
def plot_prc(name, labels, predictions, **kwargs):
precision, recall, _ = sklearn.metrics.precision_recall_curve(labels, predictions)
plt.plot(precision, recall, label=name, linewidth=2, **kwargs)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
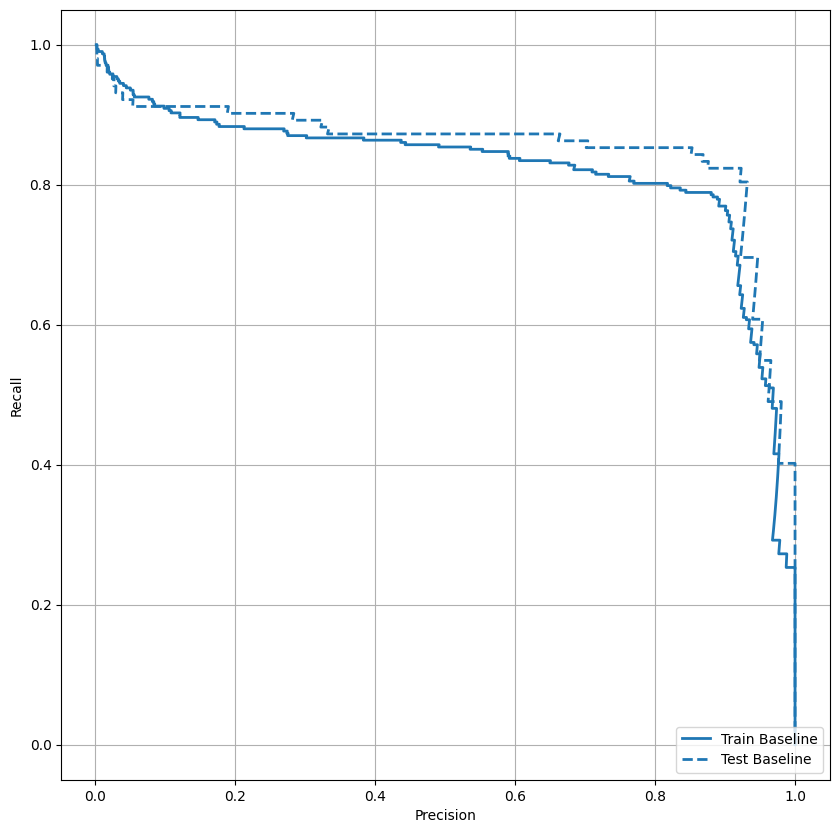
Похоже, что точность относительно высока, но отзыв и площадь под ROC-кривой (AUC) не так высоки, как хотелось бы. Классификаторы часто сталкиваются с проблемами при попытке максимизировать как точность, так и полноту, что особенно актуально при работе с несбалансированными наборами данных. Важно учитывать стоимость различных типов ошибок в контексте интересующей вас проблемы. В этом примере ложноотрицательный результат (мошенническая транзакция пропущена) может привести к финансовым затратам, а ложноположительный результат (транзакция ошибочно помечена как мошенническая) может снизить удовлетворенность пользователей.
Вес класса
Рассчитать веса классов
Цель состоит в том, чтобы идентифицировать мошеннические транзакции, но у вас не так много таких положительных образцов для работы, поэтому вы хотели бы, чтобы классификатор сильно взвешивал несколько доступных примеров. Вы можете сделать это, передав веса Keras для каждого класса через параметр. Это заставит модель «уделять больше внимания» примерам из недостаточно представленного класса.
# Scaling by total/2 helps keep the loss to a similar magnitude.
# The sum of the weights of all examples stays the same.
weight_for_0 = (1 / neg) * (total / 2.0)
weight_for_1 = (1 / pos) * (total / 2.0)
class_weight = {0: weight_for_0, 1: weight_for_1}
print('Weight for class 0: {:.2f}'.format(weight_for_0))
print('Weight for class 1: {:.2f}'.format(weight_for_1))
Weight for class 0: 0.50 Weight for class 1: 289.44
Обучите модель с весами классов
Теперь попробуйте переобучить и оценить модель с весами классов, чтобы увидеть, как это влияет на прогнозы.
weighted_model = make_model()
weighted_model.load_weights(initial_weights)
weighted_history = weighted_model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels),
# The class weights go here
class_weight=class_weight)
Epoch 1/100 90/90 [==============================] - 3s 15ms/step - loss: 4.1298 - tp: 59.0000 - fp: 11.0000 - tn: 238821.0000 - fn: 347.0000 - accuracy: 0.9985 - precision: 0.8429 - recall: 0.1453 - auc: 0.6238 - prc: 0.1649 - val_loss: 0.0119 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7124 - val_prc: 0.0294 Epoch 2/100 90/90 [==============================] - 1s 7ms/step - loss: 1.8711 - tp: 69.0000 - fp: 54.0000 - tn: 181897.0000 - fn: 256.0000 - accuracy: 0.9983 - precision: 0.5610 - recall: 0.2123 - auc: 0.8178 - prc: 0.2117 - val_loss: 0.0060 - val_tp: 56.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 30.0000 - val_accuracy: 0.9991 - val_precision: 0.8485 - val_recall: 0.6512 - val_auc: 0.9427 - val_prc: 0.6870 Epoch 3/100 90/90 [==============================] - 1s 7ms/step - loss: 0.8666 - tp: 187.0000 - fp: 198.0000 - tn: 181753.0000 - fn: 138.0000 - accuracy: 0.9982 - precision: 0.4857 - recall: 0.5754 - auc: 0.9075 - prc: 0.4912 - val_loss: 0.0077 - val_tp: 65.0000 - val_fp: 19.0000 - val_tn: 45464.0000 - val_fn: 21.0000 - val_accuracy: 0.9991 - val_precision: 0.7738 - val_recall: 0.7558 - val_auc: 0.9564 - val_prc: 0.6924 Epoch 4/100 90/90 [==============================] - 1s 7ms/step - loss: 0.6876 - tp: 218.0000 - fp: 530.0000 - tn: 181421.0000 - fn: 107.0000 - accuracy: 0.9965 - precision: 0.2914 - recall: 0.6708 - auc: 0.9152 - prc: 0.5102 - val_loss: 0.0109 - val_tp: 68.0000 - val_fp: 39.0000 - val_tn: 45444.0000 - val_fn: 18.0000 - val_accuracy: 0.9987 - val_precision: 0.6355 - val_recall: 0.7907 - val_auc: 0.9661 - val_prc: 0.6926 Epoch 5/100 90/90 [==============================] - 1s 7ms/step - loss: 0.5229 - tp: 240.0000 - fp: 1102.0000 - tn: 180849.0000 - fn: 85.0000 - accuracy: 0.9935 - precision: 0.1788 - recall: 0.7385 - auc: 0.9395 - prc: 0.5228 - val_loss: 0.0154 - val_tp: 70.0000 - val_fp: 79.0000 - val_tn: 45404.0000 - val_fn: 16.0000 - val_accuracy: 0.9979 - val_precision: 0.4698 - val_recall: 0.8140 - val_auc: 0.9657 - val_prc: 0.7023 Epoch 6/100 90/90 [==============================] - 1s 7ms/step - loss: 0.4753 - tp: 251.0000 - fp: 1839.0000 - tn: 180112.0000 - fn: 74.0000 - accuracy: 0.9895 - precision: 0.1201 - recall: 0.7723 - auc: 0.9336 - prc: 0.4297 - val_loss: 0.0213 - val_tp: 70.0000 - val_fp: 156.0000 - val_tn: 45327.0000 - val_fn: 16.0000 - val_accuracy: 0.9962 - val_precision: 0.3097 - val_recall: 0.8140 - val_auc: 0.9654 - val_prc: 0.6742 Epoch 7/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3870 - tp: 270.0000 - fp: 2554.0000 - tn: 179397.0000 - fn: 55.0000 - accuracy: 0.9857 - precision: 0.0956 - recall: 0.8308 - auc: 0.9463 - prc: 0.3800 - val_loss: 0.0269 - val_tp: 70.0000 - val_fp: 264.0000 - val_tn: 45219.0000 - val_fn: 16.0000 - val_accuracy: 0.9939 - val_precision: 0.2096 - val_recall: 0.8140 - val_auc: 0.9651 - val_prc: 0.6116 Epoch 8/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3942 - tp: 268.0000 - fp: 3219.0000 - tn: 178732.0000 - fn: 57.0000 - accuracy: 0.9820 - precision: 0.0769 - recall: 0.8246 - auc: 0.9434 - prc: 0.3273 - val_loss: 0.0337 - val_tp: 70.0000 - val_fp: 355.0000 - val_tn: 45128.0000 - val_fn: 16.0000 - val_accuracy: 0.9919 - val_precision: 0.1647 - val_recall: 0.8140 - val_auc: 0.9682 - val_prc: 0.5918 Epoch 9/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3886 - tp: 271.0000 - fp: 3845.0000 - tn: 178106.0000 - fn: 54.0000 - accuracy: 0.9786 - precision: 0.0658 - recall: 0.8338 - auc: 0.9397 - prc: 0.2995 - val_loss: 0.0386 - val_tp: 70.0000 - val_fp: 406.0000 - val_tn: 45077.0000 - val_fn: 16.0000 - val_accuracy: 0.9907 - val_precision: 0.1471 - val_recall: 0.8140 - val_auc: 0.9756 - val_prc: 0.5889 Epoch 10/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2951 - tp: 281.0000 - fp: 4348.0000 - tn: 177603.0000 - fn: 44.0000 - accuracy: 0.9759 - precision: 0.0607 - recall: 0.8646 - auc: 0.9623 - prc: 0.2826 - val_loss: 0.0441 - val_tp: 72.0000 - val_fp: 464.0000 - val_tn: 45019.0000 - val_fn: 14.0000 - val_accuracy: 0.9895 - val_precision: 0.1343 - val_recall: 0.8372 - val_auc: 0.9748 - val_prc: 0.5895 Epoch 11/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2703 - tp: 280.0000 - fp: 4697.0000 - tn: 177254.0000 - fn: 45.0000 - accuracy: 0.9740 - precision: 0.0563 - recall: 0.8615 - auc: 0.9660 - prc: 0.2589 - val_loss: 0.0490 - val_tp: 72.0000 - val_fp: 552.0000 - val_tn: 44931.0000 - val_fn: 14.0000 - val_accuracy: 0.9876 - val_precision: 0.1154 - val_recall: 0.8372 - val_auc: 0.9762 - val_prc: 0.5902 Epoch 12/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3358 - tp: 278.0000 - fp: 5262.0000 - tn: 176689.0000 - fn: 47.0000 - accuracy: 0.9709 - precision: 0.0502 - recall: 0.8554 - auc: 0.9468 - prc: 0.2368 - val_loss: 0.0534 - val_tp: 74.0000 - val_fp: 597.0000 - val_tn: 44886.0000 - val_fn: 12.0000 - val_accuracy: 0.9866 - val_precision: 0.1103 - val_recall: 0.8605 - val_auc: 0.9752 - val_prc: 0.5848 Epoch 13/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2833 - tp: 286.0000 - fp: 5502.0000 - tn: 176449.0000 - fn: 39.0000 - accuracy: 0.9696 - precision: 0.0494 - recall: 0.8800 - auc: 0.9582 - prc: 0.2572 - val_loss: 0.0563 - val_tp: 74.0000 - val_fp: 616.0000 - val_tn: 44867.0000 - val_fn: 12.0000 - val_accuracy: 0.9862 - val_precision: 0.1072 - val_recall: 0.8605 - val_auc: 0.9748 - val_prc: 0.5678 Epoch 14/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2969 - tp: 280.0000 - fp: 5630.0000 - tn: 176321.0000 - fn: 45.0000 - accuracy: 0.9689 - precision: 0.0474 - recall: 0.8615 - auc: 0.9594 - prc: 0.2374 - val_loss: 0.0597 - val_tp: 74.0000 - val_fp: 644.0000 - val_tn: 44839.0000 - val_fn: 12.0000 - val_accuracy: 0.9856 - val_precision: 0.1031 - val_recall: 0.8605 - val_auc: 0.9741 - val_prc: 0.5627 Epoch 15/100 90/90 [==============================] - ETA: 0s - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224Restoring model weights from the end of the best epoch: 5. 90/90 [==============================] - 1s 7ms/step - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224 - val_loss: 0.0621 - val_tp: 74.0000 - val_fp: 665.0000 - val_tn: 44818.0000 - val_fn: 12.0000 - val_accuracy: 0.9851 - val_precision: 0.1001 - val_recall: 0.8605 - val_auc: 0.9771 - val_prc: 0.5550 Epoch 15: early stopping
Проверить историю тренировок
plot_metrics(weighted_history)
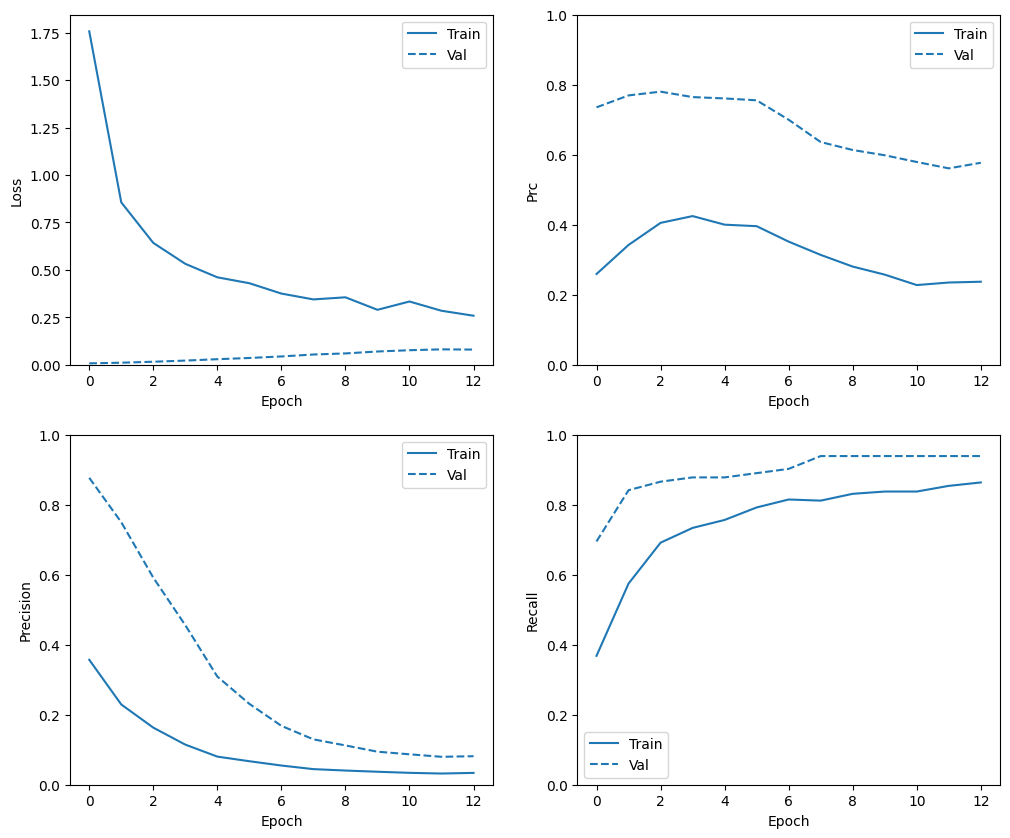
Оценить метрики
train_predictions_weighted = weighted_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_weighted = weighted_model.predict(test_features, batch_size=BATCH_SIZE)
weighted_results = weighted_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(weighted_model.metrics_names, weighted_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_weighted)
loss : 0.014327289536595345 tp : 69.0 fp : 88.0 tn : 56793.0 fn : 12.0 accuracy : 0.9982444643974304 precision : 0.4394904375076294 recall : 0.8518518805503845 auc : 0.9410961866378784 prc : 0.7397712469100952 Legitimate Transactions Detected (True Negatives): 56793 Legitimate Transactions Incorrectly Detected (False Positives): 88 Fraudulent Transactions Missed (False Negatives): 12 Fraudulent Transactions Detected (True Positives): 69 Total Fraudulent Transactions: 81
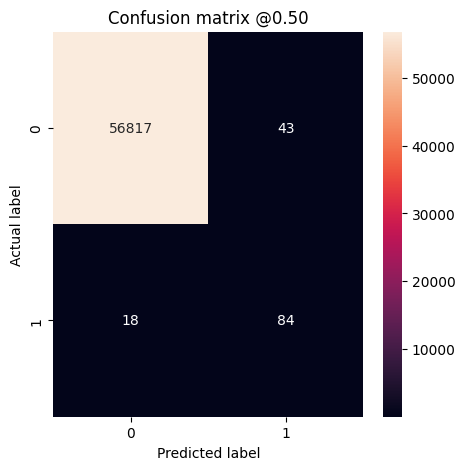
Здесь вы можете видеть, что с весами классов точность и достоверность ниже, потому что больше ложных срабатываний, но, наоборот, полнота и AUC выше, потому что модель также нашла больше истинных срабатываний. Несмотря на более низкую точность, эта модель имеет более высокую полноту (и выявляет больше мошеннических транзакций). Конечно, оба типа ошибок имеют свою цену (вы также не хотели бы обманывать пользователей, помечая слишком много законных транзакций как мошеннические). Внимательно рассмотрите компромиссы между этими различными типами ошибок для вашего приложения.
Постройте ОКР
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
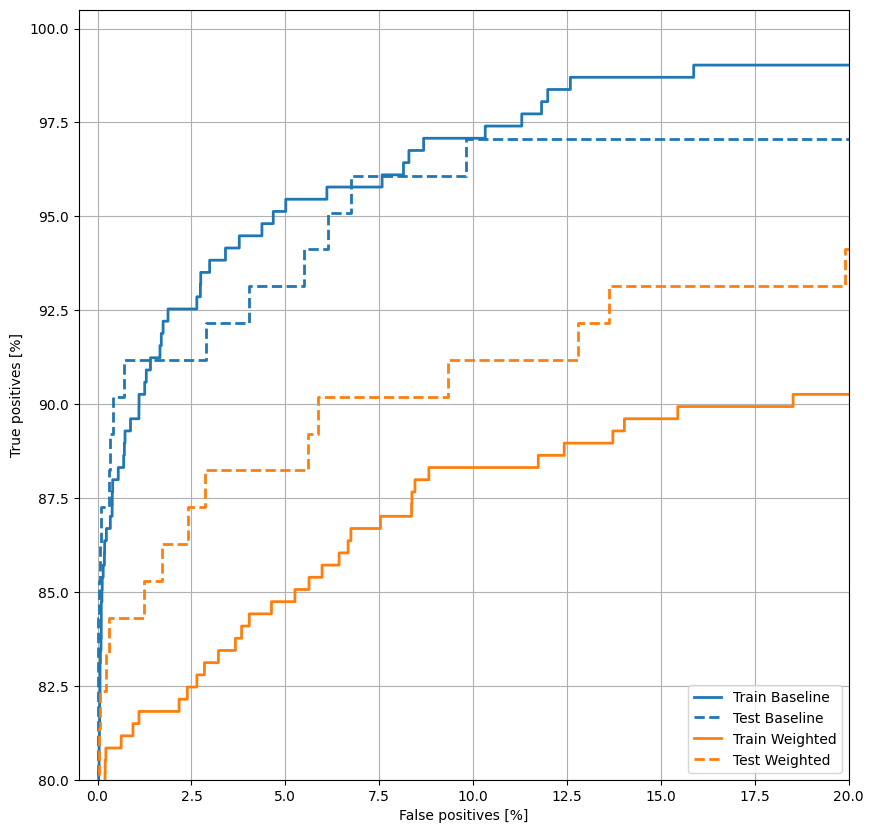
Постройте AUPRC
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
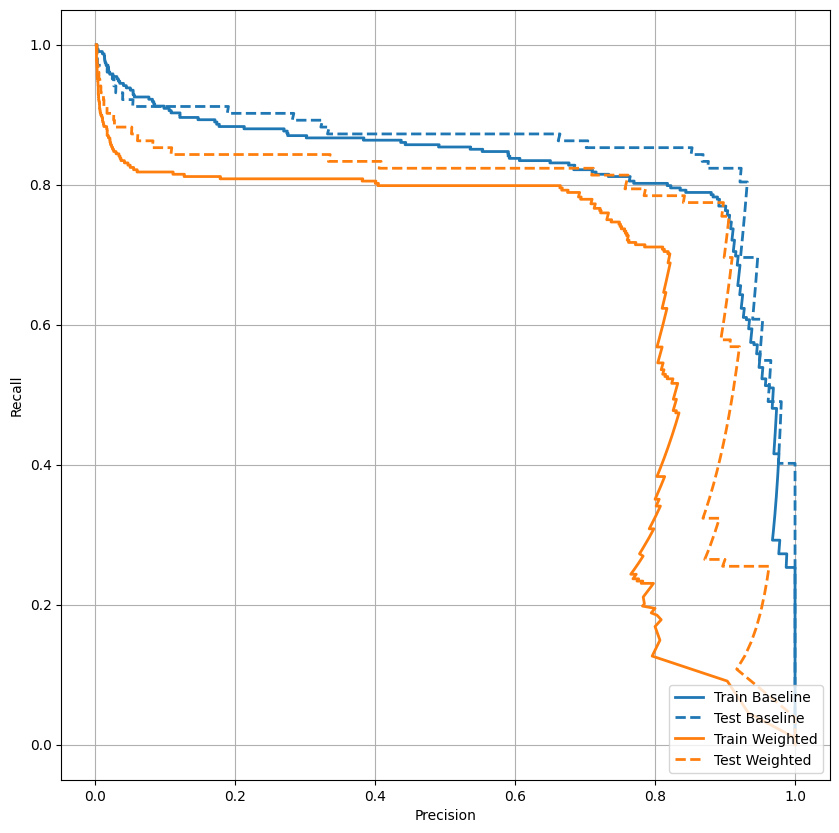
Передискретизация
Передискретизируйте класс меньшинства
Связанный подход мог бы заключаться в повторной выборке набора данных путем передискретизации класса меньшинства.
pos_features = train_features[bool_train_labels]
neg_features = train_features[~bool_train_labels]
pos_labels = train_labels[bool_train_labels]
neg_labels = train_labels[~bool_train_labels]
Использование NumPy
Вы можете сбалансировать набор данных вручную, выбрав нужное количество случайных индексов из положительных примеров:
ids = np.arange(len(pos_features))
choices = np.random.choice(ids, len(neg_features))
res_pos_features = pos_features[choices]
res_pos_labels = pos_labels[choices]
res_pos_features.shape
(181951, 29)
resampled_features = np.concatenate([res_pos_features, neg_features], axis=0)
resampled_labels = np.concatenate([res_pos_labels, neg_labels], axis=0)
order = np.arange(len(resampled_labels))
np.random.shuffle(order)
resampled_features = resampled_features[order]
resampled_labels = resampled_labels[order]
resampled_features.shape
(363902, 29)
Использование tf.data
Если вы используете tf.data , самый простой способ создать сбалансированные примеры — начать с positive и negative набора данных и объединить их. Дополнительные примеры см. в руководстве по tf.data .
BUFFER_SIZE = 100000
def make_ds(features, labels):
ds = tf.data.Dataset.from_tensor_slices((features, labels))#.cache()
ds = ds.shuffle(BUFFER_SIZE).repeat()
return ds
pos_ds = make_ds(pos_features, pos_labels)
neg_ds = make_ds(neg_features, neg_labels)
Каждый набор данных предоставляет пары (feature, label) :
for features, label in pos_ds.take(1):
print("Features:\n", features.numpy())
print()
print("Label: ", label.numpy())
Features: [ 0.56826828 1.24841849 -2.52251105 3.84165891 0.05052604 -0.7621795 -1.43118352 0.43296139 -1.85102109 -2.50477555 3.20133397 -3.52460861 -0.95133935 -5. -1.93144512 -0.7302767 -2.46735228 0.21827555 -1.45046438 0.21081234 0.39176826 -0.23558789 -0.03611637 -0.62063738 0.3686766 0.23622961 1.2242418 0.75555829 -1.45589162] Label: 1
Объедините их вместе, используя tf.data.Dataset.sample_from_datasets :
resampled_ds = tf.data.Dataset.sample_from_datasets([pos_ds, neg_ds], weights=[0.5, 0.5])
resampled_ds = resampled_ds.batch(BATCH_SIZE).prefetch(2)
for features, label in resampled_ds.take(1):
print(label.numpy().mean())
0.50732421875
Чтобы использовать этот набор данных, вам понадобится количество шагов за эпоху.
Определение «эпохи» в данном случае менее ясно. Скажем, это количество пакетов, необходимое для просмотра каждого отрицательного примера один раз:
resampled_steps_per_epoch = np.ceil(2.0*neg/BATCH_SIZE)
resampled_steps_per_epoch
278.0
Тренируйтесь на данных передискретизации
Теперь попробуйте обучить модель с набором данных с повторной выборкой вместо использования весов классов, чтобы увидеть, как эти методы сравниваются.
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
val_ds = tf.data.Dataset.from_tensor_slices((val_features, val_labels)).cache()
val_ds = val_ds.batch(BATCH_SIZE).prefetch(2)
resampled_history = resampled_model.fit(
resampled_ds,
epochs=EPOCHS,
steps_per_epoch=resampled_steps_per_epoch,
callbacks=[early_stopping],
validation_data=val_ds)
Epoch 1/100 278/278 [==============================] - 10s 32ms/step - loss: 0.5508 - tp: 214194.0000 - fp: 51114.0000 - tn: 290615.0000 - fn: 70383.0000 - accuracy: 0.8060 - precision: 0.8073 - recall: 0.7527 - auc: 0.8600 - prc: 0.8879 - val_loss: 0.2279 - val_tp: 73.0000 - val_fp: 969.0000 - val_tn: 44514.0000 - val_fn: 13.0000 - val_accuracy: 0.9785 - val_precision: 0.0701 - val_recall: 0.8488 - val_auc: 0.9551 - val_prc: 0.7044 Epoch 2/100 278/278 [==============================] - 8s 28ms/step - loss: 0.2235 - tp: 253877.0000 - fp: 15743.0000 - tn: 268530.0000 - fn: 31194.0000 - accuracy: 0.9176 - precision: 0.9416 - recall: 0.8906 - auc: 0.9658 - prc: 0.9746 - val_loss: 0.1367 - val_tp: 73.0000 - val_fp: 777.0000 - val_tn: 44706.0000 - val_fn: 13.0000 - val_accuracy: 0.9827 - val_precision: 0.0859 - val_recall: 0.8488 - val_auc: 0.9596 - val_prc: 0.7072 Epoch 3/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1785 - tp: 258572.0000 - fp: 9840.0000 - tn: 274878.0000 - fn: 26054.0000 - accuracy: 0.9370 - precision: 0.9633 - recall: 0.9085 - auc: 0.9773 - prc: 0.9827 - val_loss: 0.1023 - val_tp: 72.0000 - val_fp: 699.0000 - val_tn: 44784.0000 - val_fn: 14.0000 - val_accuracy: 0.9844 - val_precision: 0.0934 - val_recall: 0.8372 - val_auc: 0.9632 - val_prc: 0.7032 Epoch 4/100 278/278 [==============================] - 8s 29ms/step - loss: 0.1571 - tp: 260447.0000 - fp: 8085.0000 - tn: 276389.0000 - fn: 24423.0000 - accuracy: 0.9429 - precision: 0.9699 - recall: 0.9143 - auc: 0.9826 - prc: 0.9863 - val_loss: 0.0869 - val_tp: 74.0000 - val_fp: 701.0000 - val_tn: 44782.0000 - val_fn: 12.0000 - val_accuracy: 0.9844 - val_precision: 0.0955 - val_recall: 0.8605 - val_auc: 0.9633 - val_prc: 0.6972 Epoch 5/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1440 - tp: 261457.0000 - fp: 7449.0000 - tn: 277093.0000 - fn: 23345.0000 - accuracy: 0.9459 - precision: 0.9723 - recall: 0.9180 - auc: 0.9855 - prc: 0.9883 - val_loss: 0.0774 - val_tp: 73.0000 - val_fp: 679.0000 - val_tn: 44804.0000 - val_fn: 13.0000 - val_accuracy: 0.9848 - val_precision: 0.0971 - val_recall: 0.8488 - val_auc: 0.9645 - val_prc: 0.6971 Epoch 6/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1349 - tp: 262460.0000 - fp: 6942.0000 - tn: 277723.0000 - fn: 22219.0000 - accuracy: 0.9488 - precision: 0.9742 - recall: 0.9220 - auc: 0.9876 - prc: 0.9896 - val_loss: 0.0718 - val_tp: 74.0000 - val_fp: 624.0000 - val_tn: 44859.0000 - val_fn: 12.0000 - val_accuracy: 0.9860 - val_precision: 0.1060 - val_recall: 0.8605 - val_auc: 0.9645 - val_prc: 0.6891 Epoch 7/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1264 - tp: 263166.0000 - fp: 6780.0000 - tn: 278253.0000 - fn: 21145.0000 - accuracy: 0.9510 - precision: 0.9749 - recall: 0.9256 - auc: 0.9895 - prc: 0.9909 - val_loss: 0.0672 - val_tp: 75.0000 - val_fp: 602.0000 - val_tn: 44881.0000 - val_fn: 11.0000 - val_accuracy: 0.9865 - val_precision: 0.1108 - val_recall: 0.8721 - val_auc: 0.9670 - val_prc: 0.6822 Epoch 8/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1190 - tp: 264216.0000 - fp: 6569.0000 - tn: 278270.0000 - fn: 20289.0000 - accuracy: 0.9528 - precision: 0.9757 - recall: 0.9287 - auc: 0.9910 - prc: 0.9920 - val_loss: 0.0628 - val_tp: 74.0000 - val_fp: 570.0000 - val_tn: 44913.0000 - val_fn: 12.0000 - val_accuracy: 0.9872 - val_precision: 0.1149 - val_recall: 0.8605 - val_auc: 0.9671 - val_prc: 0.6830 Epoch 9/100 278/278 [==============================] - 9s 31ms/step - loss: 0.1125 - tp: 264562.0000 - fp: 6339.0000 - tn: 279137.0000 - fn: 19306.0000 - accuracy: 0.9550 - precision: 0.9766 - recall: 0.9320 - auc: 0.9924 - prc: 0.9930 - val_loss: 0.0576 - val_tp: 74.0000 - val_fp: 544.0000 - val_tn: 44939.0000 - val_fn: 12.0000 - val_accuracy: 0.9878 - val_precision: 0.1197 - val_recall: 0.8605 - val_auc: 0.9672 - val_prc: 0.6828 Epoch 10/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1064 - tp: 266549.0000 - fp: 6112.0000 - tn: 278323.0000 - fn: 18360.0000 - accuracy: 0.9570 - precision: 0.9776 - recall: 0.9356 - auc: 0.9934 - prc: 0.9937 - val_loss: 0.0544 - val_tp: 74.0000 - val_fp: 541.0000 - val_tn: 44942.0000 - val_fn: 12.0000 - val_accuracy: 0.9879 - val_precision: 0.1203 - val_recall: 0.8605 - val_auc: 0.9638 - val_prc: 0.6827 Epoch 11/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1005 - tp: 267048.0000 - fp: 6123.0000 - tn: 278896.0000 - fn: 17277.0000 - accuracy: 0.9589 - precision: 0.9776 - recall: 0.9392 - auc: 0.9943 - prc: 0.9944 - val_loss: 0.0493 - val_tp: 74.0000 - val_fp: 500.0000 - val_tn: 44983.0000 - val_fn: 12.0000 - val_accuracy: 0.9888 - val_precision: 0.1289 - val_recall: 0.8605 - val_auc: 0.9578 - val_prc: 0.6761 Epoch 12/100 277/278 [============================>.] - ETA: 0s - loss: 0.0950 - tp: 266855.0000 - fp: 6079.0000 - tn: 277677.0000 - fn: 16685.0000 - accuracy: 0.9599 - precision: 0.9777 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949Restoring model weights from the end of the best epoch: 2. 278/278 [==============================] - 8s 29ms/step - loss: 0.0950 - tp: 267815.0000 - fp: 6094.0000 - tn: 278693.0000 - fn: 16742.0000 - accuracy: 0.9599 - precision: 0.9778 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949 - val_loss: 0.0451 - val_tp: 74.0000 - val_fp: 468.0000 - val_tn: 45015.0000 - val_fn: 12.0000 - val_accuracy: 0.9895 - val_precision: 0.1365 - val_recall: 0.8605 - val_auc: 0.9581 - val_prc: 0.6683 Epoch 12: early stopping
Если бы в процессе обучения учитывался весь набор данных при каждом обновлении градиента, эта избыточная выборка была бы в основном идентична взвешиванию класса.
Но при пакетном обучении модели, как вы сделали здесь, передискретизированные данные обеспечивают более плавный градиентный сигнал: вместо того, чтобы каждый положительный пример отображался в одном пакете с большим весом, они каждый раз отображаются во многих разных пакетах с небольшой вес.
Этот более плавный градиентный сигнал упрощает обучение модели.
Проверить историю тренировок
Обратите внимание, что распределения метрик здесь будут другими, потому что данные обучения имеют совершенно другое распределение, чем данные проверки и тестирования.
plot_metrics(resampled_history)
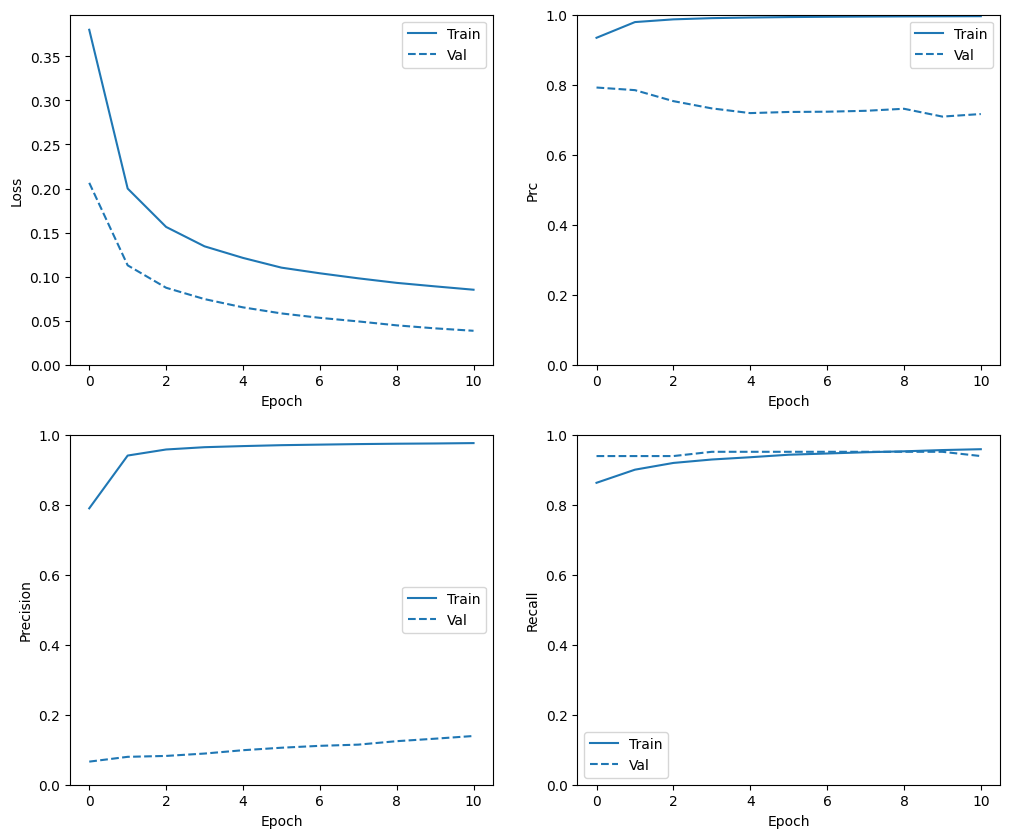
Переобучить
Поскольку обучение проще на сбалансированных данных, описанная выше процедура обучения может быстро дать переобучение.
Поэтому разбейте эпохи, чтобы дать tf.keras.callbacks.EarlyStopping более точный контроль над тем, когда останавливать обучение.
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
resampled_history = resampled_model.fit(
resampled_ds,
# These are not real epochs
steps_per_epoch=20,
epochs=10*EPOCHS,
callbacks=[early_stopping],
validation_data=(val_ds))
Epoch 1/1000 20/20 [==============================] - 3s 73ms/step - loss: 2.0114 - tp: 3382.0000 - fp: 5181.0000 - tn: 60589.0000 - fn: 17377.0000 - accuracy: 0.7393 - precision: 0.3950 - recall: 0.1629 - auc: 0.6308 - prc: 0.3325 - val_loss: 0.4343 - val_tp: 7.0000 - val_fp: 5042.0000 - val_tn: 40441.0000 - val_fn: 79.0000 - val_accuracy: 0.8876 - val_precision: 0.0014 - val_recall: 0.0814 - val_auc: 0.2282 - val_prc: 0.0012 Epoch 2/1000 20/20 [==============================] - 1s 33ms/step - loss: 1.2163 - tp: 7466.0000 - fp: 5137.0000 - tn: 15257.0000 - fn: 13100.0000 - accuracy: 0.5548 - precision: 0.5924 - recall: 0.3630 - auc: 0.4763 - prc: 0.5716 - val_loss: 0.4539 - val_tp: 36.0000 - val_fp: 5893.0000 - val_tn: 39590.0000 - val_fn: 50.0000 - val_accuracy: 0.8696 - val_precision: 0.0061 - val_recall: 0.4186 - val_auc: 0.6494 - val_prc: 0.0054 Epoch 3/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.7406 - tp: 12289.0000 - fp: 5509.0000 - tn: 14872.0000 - fn: 8290.0000 - accuracy: 0.6631 - precision: 0.6905 - recall: 0.5972 - auc: 0.6803 - prc: 0.7580 - val_loss: 0.4611 - val_tp: 75.0000 - val_fp: 6273.0000 - val_tn: 39210.0000 - val_fn: 11.0000 - val_accuracy: 0.8621 - val_precision: 0.0118 - val_recall: 0.8721 - val_auc: 0.9293 - val_prc: 0.4539 Epoch 4/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.5071 - tp: 15891.0000 - fp: 5370.0000 - tn: 15013.0000 - fn: 4686.0000 - accuracy: 0.7545 - precision: 0.7474 - recall: 0.7723 - auc: 0.8298 - prc: 0.8757 - val_loss: 0.4451 - val_tp: 78.0000 - val_fp: 5505.0000 - val_tn: 39978.0000 - val_fn: 8.0000 - val_accuracy: 0.8790 - val_precision: 0.0140 - val_recall: 0.9070 - val_auc: 0.9443 - val_prc: 0.6777 Epoch 5/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.4284 - tp: 17046.0000 - fp: 5072.0000 - tn: 15496.0000 - fn: 3346.0000 - accuracy: 0.7945 - precision: 0.7707 - recall: 0.8359 - auc: 0.8827 - prc: 0.9151 - val_loss: 0.4140 - val_tp: 77.0000 - val_fp: 4338.0000 - val_tn: 41145.0000 - val_fn: 9.0000 - val_accuracy: 0.9046 - val_precision: 0.0174 - val_recall: 0.8953 - val_auc: 0.9463 - val_prc: 0.6903 Epoch 6/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.3836 - tp: 17606.0000 - fp: 4362.0000 - tn: 16113.0000 - fn: 2879.0000 - accuracy: 0.8232 - precision: 0.8014 - recall: 0.8595 - auc: 0.9080 - prc: 0.9336 - val_loss: 0.3824 - val_tp: 77.0000 - val_fp: 3314.0000 - val_tn: 42169.0000 - val_fn: 9.0000 - val_accuracy: 0.9271 - val_precision: 0.0227 - val_recall: 0.8953 - val_auc: 0.9475 - val_prc: 0.6752 Epoch 7/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3574 - tp: 17856.0000 - fp: 3894.0000 - tn: 16553.0000 - fn: 2657.0000 - accuracy: 0.8401 - precision: 0.8210 - recall: 0.8705 - auc: 0.9208 - prc: 0.9432 - val_loss: 0.3538 - val_tp: 76.0000 - val_fp: 2592.0000 - val_tn: 42891.0000 - val_fn: 10.0000 - val_accuracy: 0.9429 - val_precision: 0.0285 - val_recall: 0.8837 - val_auc: 0.9486 - val_prc: 0.6819 Epoch 8/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3377 - tp: 17766.0000 - fp: 3483.0000 - tn: 17067.0000 - fn: 2644.0000 - accuracy: 0.8504 - precision: 0.8361 - recall: 0.8705 - auc: 0.9280 - prc: 0.9481 - val_loss: 0.3271 - val_tp: 76.0000 - val_fp: 2047.0000 - val_tn: 43436.0000 - val_fn: 10.0000 - val_accuracy: 0.9549 - val_precision: 0.0358 - val_recall: 0.8837 - val_auc: 0.9497 - val_prc: 0.6910 Epoch 9/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3188 - tp: 17749.0000 - fp: 2855.0000 - tn: 17547.0000 - fn: 2809.0000 - accuracy: 0.8617 - precision: 0.8614 - recall: 0.8634 - auc: 0.9360 - prc: 0.9539 - val_loss: 0.3051 - val_tp: 74.0000 - val_fp: 1657.0000 - val_tn: 43826.0000 - val_fn: 12.0000 - val_accuracy: 0.9634 - val_precision: 0.0427 - val_recall: 0.8605 - val_auc: 0.9514 - val_prc: 0.7022 Epoch 10/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.3046 - tp: 17772.0000 - fp: 2599.0000 - tn: 17841.0000 - fn: 2748.0000 - accuracy: 0.8695 - precision: 0.8724 - recall: 0.8661 - auc: 0.9402 - prc: 0.9570 - val_loss: 0.2860 - val_tp: 74.0000 - val_fp: 1398.0000 - val_tn: 44085.0000 - val_fn: 12.0000 - val_accuracy: 0.9691 - val_precision: 0.0503 - val_recall: 0.8605 - val_auc: 0.9527 - val_prc: 0.6997 Epoch 11/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2937 - tp: 17673.0000 - fp: 2352.0000 - tn: 18273.0000 - fn: 2662.0000 - accuracy: 0.8776 - precision: 0.8825 - recall: 0.8691 - auc: 0.9447 - prc: 0.9595 - val_loss: 0.2687 - val_tp: 73.0000 - val_fp: 1235.0000 - val_tn: 44248.0000 - val_fn: 13.0000 - val_accuracy: 0.9726 - val_precision: 0.0558 - val_recall: 0.8488 - val_auc: 0.9534 - val_prc: 0.7066 Epoch 12/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2813 - tp: 17721.0000 - fp: 2109.0000 - tn: 18523.0000 - fn: 2607.0000 - accuracy: 0.8849 - precision: 0.8936 - recall: 0.8718 - auc: 0.9485 - prc: 0.9621 - val_loss: 0.2524 - val_tp: 73.0000 - val_fp: 1098.0000 - val_tn: 44385.0000 - val_fn: 13.0000 - val_accuracy: 0.9756 - val_precision: 0.0623 - val_recall: 0.8488 - val_auc: 0.9539 - val_prc: 0.7094 Epoch 13/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2706 - tp: 18031.0000 - fp: 1869.0000 - tn: 18502.0000 - fn: 2558.0000 - accuracy: 0.8919 - precision: 0.9061 - recall: 0.8758 - auc: 0.9520 - prc: 0.9652 - val_loss: 0.2395 - val_tp: 73.0000 - val_fp: 1037.0000 - val_tn: 44446.0000 - val_fn: 13.0000 - val_accuracy: 0.9770 - val_precision: 0.0658 - val_recall: 0.8488 - val_auc: 0.9549 - val_prc: 0.7119 Epoch 14/1000 20/20 [==============================] - 1s 37ms/step - loss: 0.2665 - tp: 18087.0000 - fp: 1748.0000 - tn: 18567.0000 - fn: 2558.0000 - accuracy: 0.8949 - precision: 0.9119 - recall: 0.8761 - auc: 0.9525 - prc: 0.9661 - val_loss: 0.2283 - val_tp: 73.0000 - val_fp: 972.0000 - val_tn: 44511.0000 - val_fn: 13.0000 - val_accuracy: 0.9784 - val_precision: 0.0699 - val_recall: 0.8488 - val_auc: 0.9556 - val_prc: 0.7045 Epoch 15/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2589 - tp: 18064.0000 - fp: 1630.0000 - tn: 18830.0000 - fn: 2436.0000 - accuracy: 0.9007 - precision: 0.9172 - recall: 0.8812 - auc: 0.9560 - prc: 0.9676 - val_loss: 0.2180 - val_tp: 73.0000 - val_fp: 941.0000 - val_tn: 44542.0000 - val_fn: 13.0000 - val_accuracy: 0.9791 - val_precision: 0.0720 - val_recall: 0.8488 - val_auc: 0.9563 - val_prc: 0.7069 Epoch 16/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2495 - tp: 18132.0000 - fp: 1481.0000 - tn: 18926.0000 - fn: 2421.0000 - accuracy: 0.9047 - precision: 0.9245 - recall: 0.8822 - auc: 0.9587 - prc: 0.9695 - val_loss: 0.2079 - val_tp: 73.0000 - val_fp: 905.0000 - val_tn: 44578.0000 - val_fn: 13.0000 - val_accuracy: 0.9799 - val_precision: 0.0746 - val_recall: 0.8488 - val_auc: 0.9565 - val_prc: 0.7110 Epoch 17/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2435 - tp: 18047.0000 - fp: 1378.0000 - tn: 19144.0000 - fn: 2391.0000 - accuracy: 0.9080 - precision: 0.9291 - recall: 0.8830 - auc: 0.9601 - prc: 0.9706 - val_loss: 0.1990 - val_tp: 73.0000 - val_fp: 882.0000 - val_tn: 44601.0000 - val_fn: 13.0000 - val_accuracy: 0.9804 - val_precision: 0.0764 - val_recall: 0.8488 - val_auc: 0.9568 - val_prc: 0.7118 Epoch 18/1000 20/20 [==============================] - 1s 37ms/step - loss: 0.2396 - tp: 18223.0000 - fp: 1289.0000 - tn: 19075.0000 - fn: 2373.0000 - accuracy: 0.9106 - precision: 0.9339 - recall: 0.8848 - auc: 0.9612 - prc: 0.9714 - val_loss: 0.1911 - val_tp: 73.0000 - val_fp: 870.0000 - val_tn: 44613.0000 - val_fn: 13.0000 - val_accuracy: 0.9806 - val_precision: 0.0774 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7148 Epoch 19/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2324 - tp: 18179.0000 - fp: 1205.0000 - tn: 19254.0000 - fn: 2322.0000 - accuracy: 0.9139 - precision: 0.9378 - recall: 0.8867 - auc: 0.9633 - prc: 0.9728 - val_loss: 0.1839 - val_tp: 73.0000 - val_fp: 857.0000 - val_tn: 44626.0000 - val_fn: 13.0000 - val_accuracy: 0.9809 - val_precision: 0.0785 - val_recall: 0.8488 - val_auc: 0.9576 - val_prc: 0.7165 Epoch 20/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2318 - tp: 18119.0000 - fp: 1224.0000 - tn: 19279.0000 - fn: 2338.0000 - accuracy: 0.9130 - precision: 0.9367 - recall: 0.8857 - auc: 0.9640 - prc: 0.9728 - val_loss: 0.1758 - val_tp: 73.0000 - val_fp: 823.0000 - val_tn: 44660.0000 - val_fn: 13.0000 - val_accuracy: 0.9817 - val_precision: 0.0815 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7185 Epoch 21/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2233 - tp: 18041.0000 - fp: 1074.0000 - tn: 19514.0000 - fn: 2331.0000 - accuracy: 0.9169 - precision: 0.9438 - recall: 0.8856 - auc: 0.9660 - prc: 0.9745 - val_loss: 0.1690 - val_tp: 73.0000 - val_fp: 813.0000 - val_tn: 44670.0000 - val_fn: 13.0000 - val_accuracy: 0.9819 - val_precision: 0.0824 - val_recall: 0.8488 - val_auc: 0.9578 - val_prc: 0.7211 Epoch 22/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2193 - tp: 18258.0000 - fp: 1013.0000 - tn: 19414.0000 - fn: 2275.0000 - accuracy: 0.9197 - precision: 0.9474 - recall: 0.8892 - auc: 0.9666 - prc: 0.9753 - val_loss: 0.1634 - val_tp: 73.0000 - val_fp: 817.0000 - val_tn: 44666.0000 - val_fn: 13.0000 - val_accuracy: 0.9818 - val_precision: 0.0820 - val_recall: 0.8488 - val_auc: 0.9580 - val_prc: 0.7123 Epoch 23/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2114 - tp: 18439.0000 - fp: 993.0000 - tn: 19417.0000 - fn: 2111.0000 - accuracy: 0.9242 - precision: 0.9489 - recall: 0.8973 - auc: 0.9696 - prc: 0.9774 - val_loss: 0.1577 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9584 - val_prc: 0.7122 Epoch 24/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2076 - tp: 18459.0000 - fp: 896.0000 - tn: 19582.0000 - fn: 2023.0000 - accuracy: 0.9287 - precision: 0.9537 - recall: 0.9012 - auc: 0.9694 - prc: 0.9776 - val_loss: 0.1528 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9587 - val_prc: 0.7129 Epoch 25/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2044 - tp: 18340.0000 - fp: 907.0000 - tn: 19664.0000 - fn: 2049.0000 - accuracy: 0.9278 - precision: 0.9529 - recall: 0.8995 - auc: 0.9707 - prc: 0.9783 - val_loss: 0.1483 - val_tp: 73.0000 - val_fp: 800.0000 - val_tn: 44683.0000 - val_fn: 13.0000 - val_accuracy: 0.9822 - val_precision: 0.0836 - val_recall: 0.8488 - val_auc: 0.9591 - val_prc: 0.7054 Epoch 26/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1997 - tp: 18293.0000 - fp: 918.0000 - tn: 19749.0000 - fn: 2000.0000 - accuracy: 0.9288 - precision: 0.9522 - recall: 0.9014 - auc: 0.9722 - prc: 0.9788 - val_loss: 0.1433 - val_tp: 73.0000 - val_fp: 788.0000 - val_tn: 44695.0000 - val_fn: 13.0000 - val_accuracy: 0.9824 - val_precision: 0.0848 - val_recall: 0.8488 - val_auc: 0.9590 - val_prc: 0.7059 Epoch 27/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1987 - tp: 18562.0000 - fp: 848.0000 - tn: 19530.0000 - fn: 2020.0000 - accuracy: 0.9300 - precision: 0.9563 - recall: 0.9019 - auc: 0.9720 - prc: 0.9791 - val_loss: 0.1394 - val_tp: 73.0000 - val_fp: 784.0000 - val_tn: 44699.0000 - val_fn: 13.0000 - val_accuracy: 0.9825 - val_precision: 0.0852 - val_recall: 0.8488 - val_auc: 0.9595 - val_prc: 0.7062 Epoch 28/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1944 - tp: 18320.0000 - fp: 828.0000 - tn: 19823.0000 - fn: 1989.0000 - accuracy: 0.9312 - precision: 0.9568 - recall: 0.9021 - auc: 0.9734 - prc: 0.9798 - val_loss: 0.1351 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9598 - val_prc: 0.7079 Epoch 29/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.1933 - tp: 18455.0000 - fp: 827.0000 - tn: 19704.0000 - fn: 1974.0000 - accuracy: 0.9316 - precision: 0.9571 - recall: 0.9034 - auc: 0.9732 - prc: 0.9797 - val_loss: 0.1313 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9599 - val_prc: 0.7094 Epoch 30/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.1910 - tp: 18417.0000 - fp: 768.0000 - tn: 19858.0000 - fn: 1917.0000 - accuracy: 0.9344 - precision: 0.9600 - recall: 0.9057 - auc: 0.9740 - prc: 0.9802 - val_loss: 0.1282 - val_tp: 73.0000 - val_fp: 759.0000 - val_tn: 44724.0000 - val_fn: 13.0000 - val_accuracy: 0.9831 - val_precision: 0.0877 - val_recall: 0.8488 - val_auc: 0.9602 - val_prc: 0.7094 Epoch 31/1000 20/20 [==============================] - ETA: 0s - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811Restoring model weights from the end of the best epoch: 21. 20/20 [==============================] - 1s 34ms/step - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811 - val_loss: 0.1246 - val_tp: 73.0000 - val_fp: 742.0000 - val_tn: 44741.0000 - val_fn: 13.0000 - val_accuracy: 0.9834 - val_precision: 0.0896 - val_recall: 0.8488 - val_auc: 0.9597 - val_prc: 0.7095 Epoch 31: early stopping
Перепроверьте историю тренировок
plot_metrics(resampled_history)
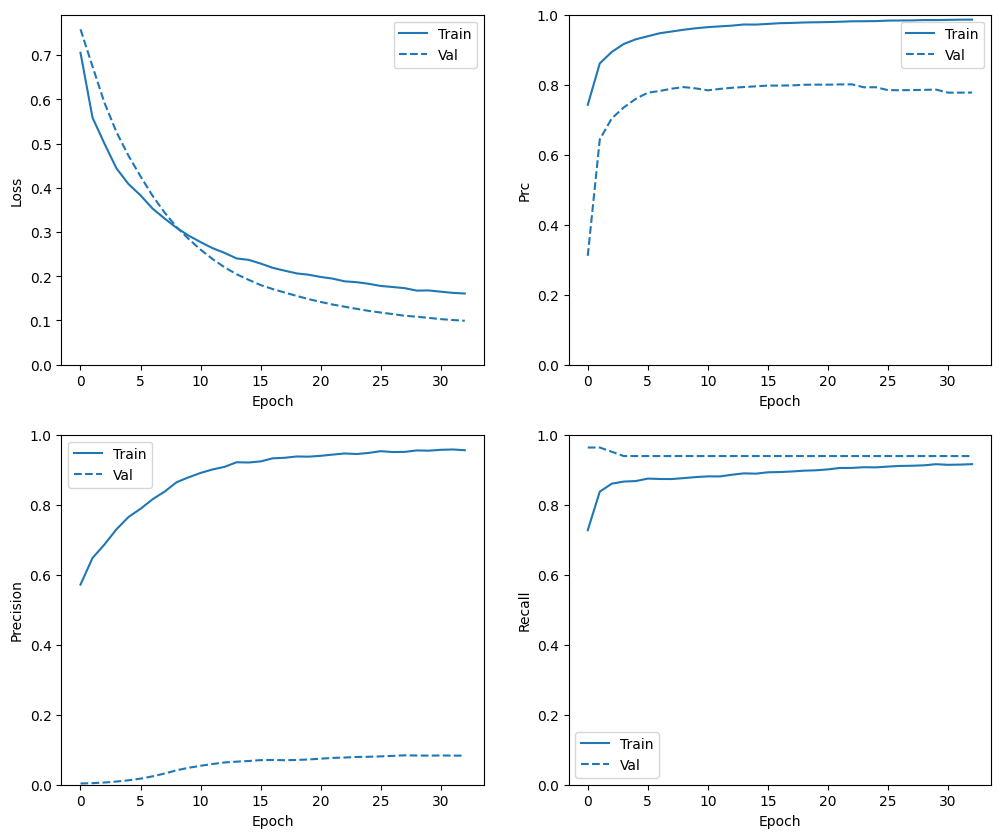
Оценить метрики
train_predictions_resampled = resampled_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_resampled = resampled_model.predict(test_features, batch_size=BATCH_SIZE)
resampled_results = resampled_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(resampled_model.metrics_names, resampled_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_resampled)
loss : 0.16882120072841644 tp : 71.0 fp : 1032.0 tn : 55849.0 fn : 10.0 accuracy : 0.9817070960998535 precision : 0.06436990201473236 recall : 0.8765432238578796 auc : 0.9518552422523499 prc : 0.7423797845840454 Legitimate Transactions Detected (True Negatives): 55849 Legitimate Transactions Incorrectly Detected (False Positives): 1032 Fraudulent Transactions Missed (False Negatives): 10 Fraudulent Transactions Detected (True Positives): 71 Total Fraudulent Transactions: 81
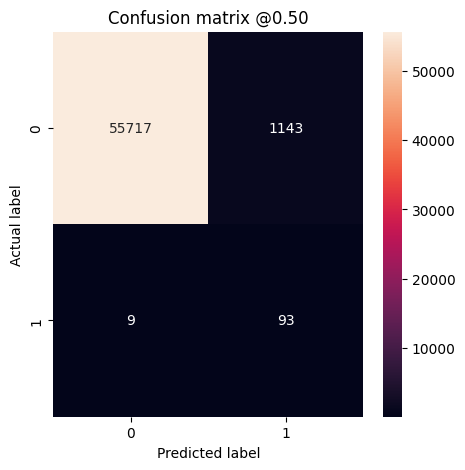
Постройте ОКР
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_roc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_roc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
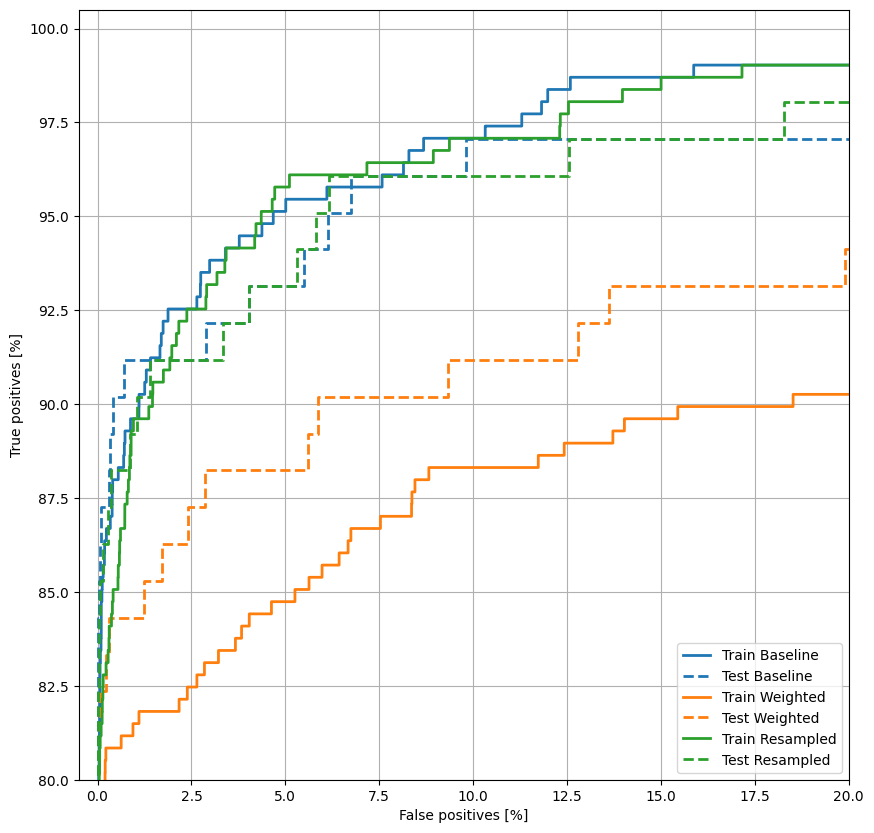
Постройте AUPRC
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_prc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_prc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
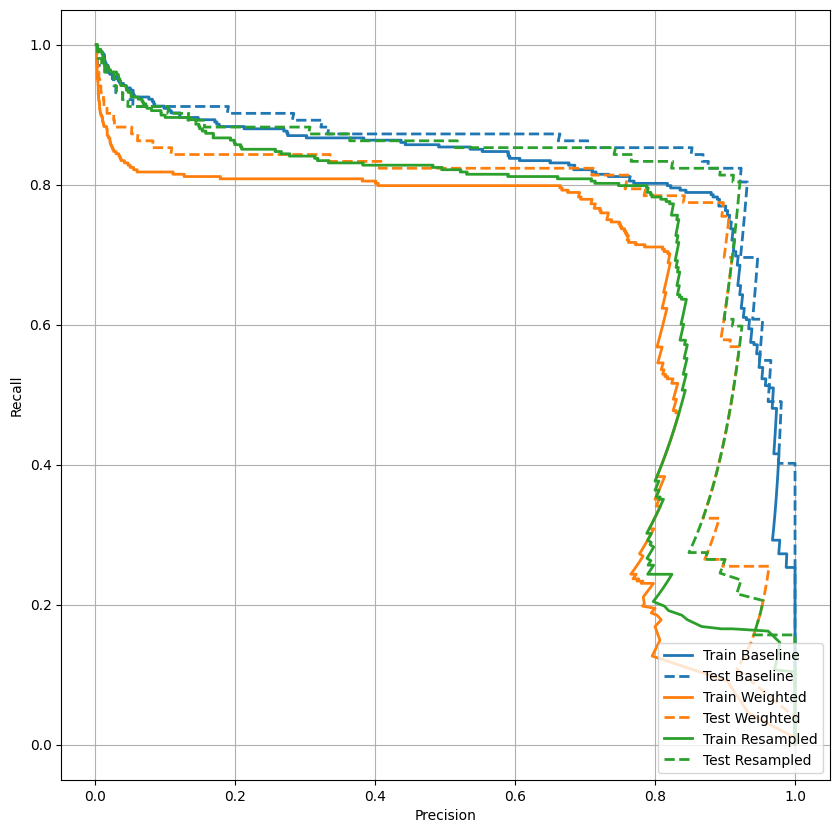
Применение этого руководства к вашей проблеме
Несбалансированная классификация данных по своей сути является сложной задачей, поскольку существует так мало примеров, на которых можно учиться. Вы всегда должны сначала начинать с данных и делать все возможное, чтобы собрать как можно больше образцов и серьезно подумать о том, какие функции могут быть важны, чтобы модель могла получить максимальную отдачу от вашего класса меньшинства. В какой-то момент ваша модель может испытывать трудности с улучшением и получением желаемых результатов, поэтому важно помнить о контексте вашей проблемы и компромиссах между различными типами ошибок.
