 TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
यह ट्यूटोरियल TensorFlow का उपयोग करके समय श्रृंखला पूर्वानुमान का परिचय है। यह कन्वर्सेशनल और आवर्तक तंत्रिका नेटवर्क (सीएनएन और आरएनएन) सहित मॉडलों की कुछ अलग शैलियों का निर्माण करता है।
यह उपखंडों के साथ दो मुख्य भागों में शामिल है:
- सिंगल टाइम स्टेप के लिए पूर्वानुमान:
- एक ही विशेषता।
- सभी सुविधाएं।
- कई चरणों का पूर्वानुमान:
- सिंगल-शॉट: भविष्यवाणियां एक ही बार में करें।
- ऑटोरेग्रेसिव: एक बार में एक भविष्यवाणी करें और आउटपुट को वापस मॉडल में फीड करें।
सेट अप
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
मौसम डेटासेट
यह ट्यूटोरियल मैक्स प्लैंक इंस्टीट्यूट फॉर बायोगेकेमिस्ट्री द्वारा रिकॉर्ड किए गए मौसम समय श्रृंखला डेटासेट का उपयोग करता है।
इस डेटासेट में 14 अलग-अलग विशेषताएं हैं जैसे हवा का तापमान, वायुमंडलीय दबाव और आर्द्रता। ये 2003 से शुरू होकर हर 10 मिनट में एकत्र किए गए थे। दक्षता के लिए, आप केवल 2009 और 2016 के बीच एकत्र किए गए डेटा का उपयोग करेंगे। डेटासेट का यह खंड फ्रांकोइस चॉलेट द्वारा अपनी पुस्तक डीप लर्निंग विद पायथन के लिए तैयार किया गया था।
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
यह ट्यूटोरियल केवल प्रति घंटा भविष्यवाणियों से निपटेगा, इसलिए डेटा को 10 मिनट के अंतराल से एक घंटे के अंतराल तक उप-नमूना करके शुरू करें:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
आइए आंकड़ों पर एक नजर डालते हैं। यहाँ पहली कुछ पंक्तियाँ हैं:
df.head()
यहाँ समय के साथ कुछ विशेषताओं का विकास हुआ है:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
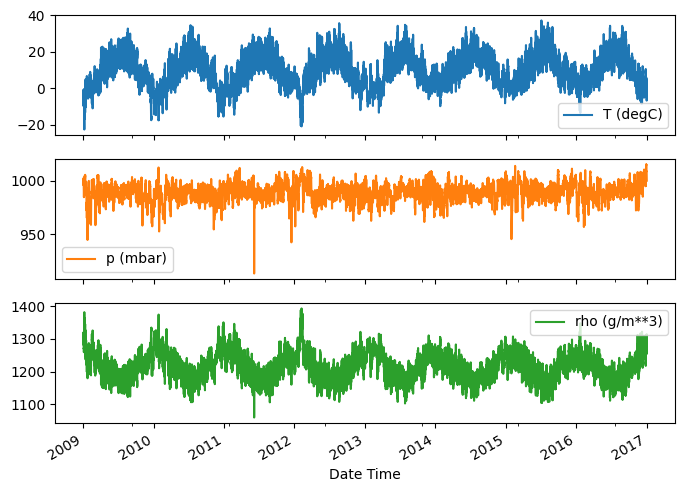

निरीक्षण और सफाई
इसके बाद, डेटासेट के आँकड़ों को देखें:
df.describe().transpose()
पवन वेग
हवा के वेग ( wv (m/s) ) का min मान और अधिकतम मान ( max. wv (m/s) ) कॉलम में एक चीज जो सबसे अलग होनी चाहिए, वह है। यह -9999 संभावित रूप से गलत है।
हवा की दिशा का एक अलग कॉलम है, इसलिए वेग शून्य ( >=0 ) से अधिक होना चाहिए। इसे शून्य से बदलें:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
फ़ीचर इंजीनियरिंग
एक मॉडल बनाने के लिए गोता लगाने से पहले, अपने डेटा को समझना और यह सुनिश्चित करना महत्वपूर्ण है कि आप मॉडल को उचित रूप से स्वरूपित डेटा पास कर रहे हैं।
हवा
डेटा का अंतिम कॉलम, wd (deg) - डिग्री की इकाइयों में हवा की दिशा देता है। कोण अच्छे मॉडल इनपुट नहीं बनाते हैं: 360° और 0° एक-दूसरे के करीब होने चाहिए और आसानी से चारों ओर लपेटे जाने चाहिए। अगर हवा नहीं चल रही है तो दिशा मायने नहीं रखती।
अभी पवन डेटा का वितरण इस तरह दिखता है:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
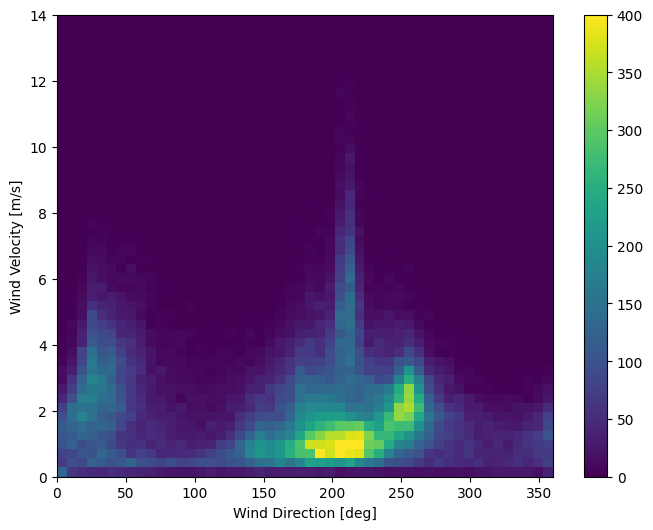
लेकिन अगर आप हवा की दिशा और वेग कॉलम को विंड वेक्टर में बदलते हैं तो मॉडल की व्याख्या करना आसान होगा:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
मॉडल के लिए सही ढंग से व्याख्या करने के लिए पवन वैक्टर का वितरण बहुत आसान है:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
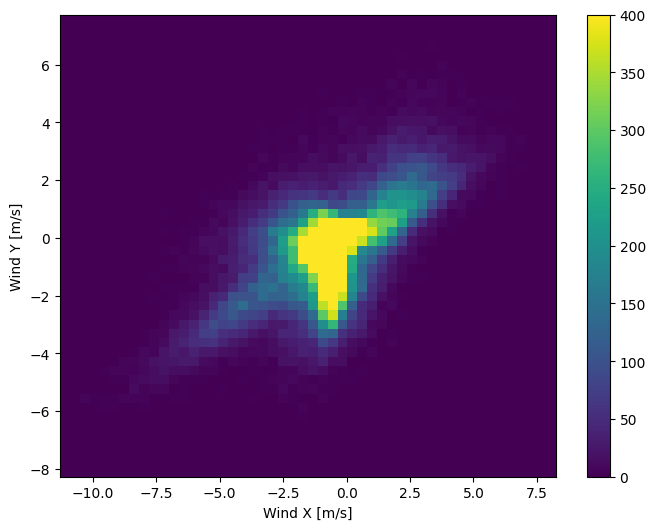
समय
इसी तरह, Date Time कॉलम बहुत उपयोगी है, लेकिन इस स्ट्रिंग फॉर्म में नहीं। इसे सेकंड में परिवर्तित करके प्रारंभ करें:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
हवा की दिशा के समान, सेकंड में समय एक उपयोगी मॉडल इनपुट नहीं है। मौसम के आंकड़े होने के कारण, इसकी दैनिक और वार्षिक आवधिकता स्पष्ट है। ऐसे कई तरीके हैं जिनसे आप आवधिकता से निपट सकते हैं।
आप "दिन का समय" और "वर्ष का समय" संकेतों को साफ़ करने के लिए साइन और कोसाइन ट्रांसफ़ॉर्म का उपयोग करके प्रयोग करने योग्य सिग्नल प्राप्त कर सकते हैं:
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')

यह मॉडल को सबसे महत्वपूर्ण आवृत्ति सुविधाओं तक पहुंच प्रदान करता है। इस मामले में आप समय से पहले जानते थे कि कौन सी आवृत्तियां महत्वपूर्ण थीं।
यदि आपके पास वह जानकारी नहीं है, तो आप फास्ट फूरियर ट्रांसफॉर्म के साथ सुविधाओं को निकालने के द्वारा निर्धारित कर सकते हैं कि कौन सी आवृत्तियां महत्वपूर्ण हैं। मान्यताओं की जाँच करने के लिए, यहाँ समय के साथ तापमान का tf.signal.rfft है। 1/year और 1/day के करीब आवृत्तियों पर स्पष्ट चोटियों पर ध्यान दें:
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
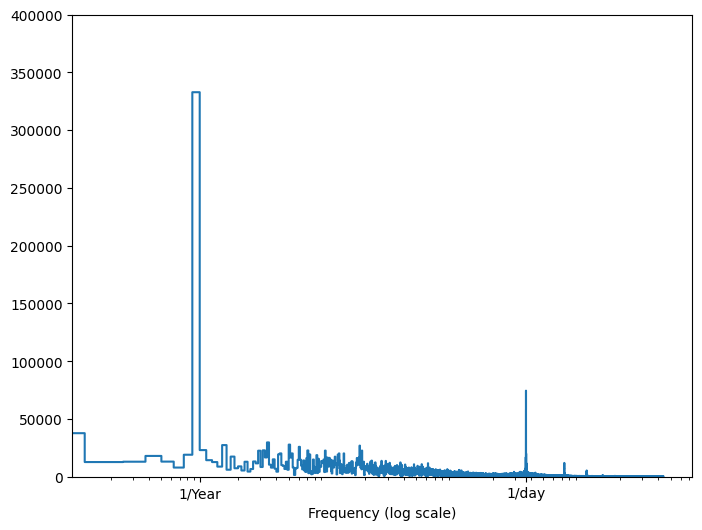
डेटा विभाजित करें
आप प्रशिक्षण, सत्यापन और परीक्षण सेट के लिए (70%, 20%, 10%) विभाजन का उपयोग करेंगे। ध्यान दें कि बंटवारे से पहले डेटा को बेतरतीब ढंग से फेरबदल नहीं किया जा रहा है। ऐसा दो कारणों से है:
- यह सुनिश्चित करता है कि डेटा को लगातार नमूनों की विंडो में काटना अभी भी संभव है।
- यह सुनिश्चित करता है कि सत्यापन / परीक्षण के परिणाम अधिक यथार्थवादी हैं, मॉडल के प्रशिक्षण के बाद एकत्र किए गए डेटा पर मूल्यांकन किया जा रहा है।
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
डेटा को सामान्य करें
तंत्रिका नेटवर्क को प्रशिक्षित करने से पहले सुविधाओं को स्केल करना महत्वपूर्ण है। सामान्यीकरण इस स्केलिंग को करने का एक सामान्य तरीका है: माध्य घटाएं और प्रत्येक सुविधा के मानक विचलन से विभाजित करें।
माध्य और मानक विचलन की गणना केवल प्रशिक्षण डेटा का उपयोग करके की जानी चाहिए ताकि मॉडल की सत्यापन और परीक्षण सेट में मानों तक कोई पहुंच न हो।
यह भी तर्कपूर्ण है कि प्रशिक्षण के दौरान मॉडल को प्रशिक्षण सेट में भविष्य के मूल्यों तक पहुंच नहीं होनी चाहिए, और यह सामान्यीकरण चलती औसत का उपयोग करके किया जाना चाहिए। यह इस ट्यूटोरियल का फोकस नहीं है, और सत्यापन और परीक्षण सेट यह सुनिश्चित करते हैं कि आपको (कुछ हद तक) ईमानदार मेट्रिक्स मिले। तो, सादगी के हित में यह ट्यूटोरियल एक साधारण औसत का उपयोग करता है।
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
अब, सुविधाओं के वितरण पर नज़र डालें। कुछ विशेषताओं में लंबी पूंछ होती है, लेकिन -9999 पवन वेग मान जैसी कोई स्पष्ट त्रुटि नहीं होती है।
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

डेटा विंडोिंग
इस ट्यूटोरियल के मॉडल डेटा से लगातार नमूनों की एक विंडो के आधार पर भविष्यवाणियों का एक सेट बनाएंगे।
इनपुट विंडो की मुख्य विशेषताएं हैं:
- इनपुट और लेबल विंडो की चौड़ाई (समय चरणों की संख्या)।
- उनके बीच का समय ऑफसेट।
- इनपुट, लेबल या दोनों के रूप में किन विशेषताओं का उपयोग किया जाता है।
यह ट्यूटोरियल विभिन्न प्रकार के मॉडल बनाता है (रैखिक, डीएनएन, सीएनएन और आरएनएन मॉडल सहित), और दोनों के लिए उनका उपयोग करता है:
- एकल-आउटपुट और बहु-आउटपुट पूर्वानुमान।
- सिंगल-टाइम-स्टेप और मल्टी-टाइम-स्टेप प्रेडिक्शन।
यह खंड डेटा विंडोिंग को लागू करने पर केंद्रित है ताकि उन सभी मॉडलों के लिए इसका पुन: उपयोग किया जा सके।
कार्य और मॉडल के प्रकार के आधार पर आप विभिन्न प्रकार की डेटा विंडो उत्पन्न करना चाह सकते हैं। यहां कुछ उदाहरण दिए गए हैं:
उदाहरण के लिए, 24 घंटे के इतिहास को देखते हुए, भविष्य में 24 घंटे की एक भविष्यवाणी करने के लिए, आप इस तरह एक विंडो परिभाषित कर सकते हैं:
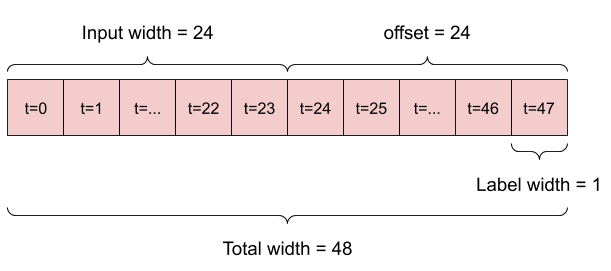
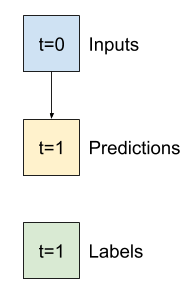
एक मॉडल जो भविष्य में एक घंटे की भविष्यवाणी करता है, छह घंटे के इतिहास को देखते हुए, उसे इस तरह की एक खिड़की की आवश्यकता होगी:

इस खंड का शेष भाग WindowGenerator वर्ग को परिभाषित करता है। यह वर्ग कर सकता है:
- इंडेक्स और ऑफ़सेट को हैंडल करें जैसा कि ऊपर दिए गए डायग्राम में दिखाया गया है।
- सुविधाओं की विंडो को
(features, labels)जोड़े में विभाजित करें। - परिणामी विंडो की सामग्री को प्लॉट करें।
-
tf.data.Datasets का उपयोग करके, प्रशिक्षण, मूल्यांकन और परीक्षण डेटा से इन विंडो के बैच को कुशलतापूर्वक उत्पन्न करें।
1. इंडेक्स और ऑफ़सेट
WindowGenerator वर्ग बनाकर प्रारंभ करें। __init__ विधि में इनपुट और लेबल सूचकांकों के लिए सभी आवश्यक तर्क शामिल हैं।
यह इनपुट के रूप में प्रशिक्षण, मूल्यांकन और डेटाफ़्रेम का परीक्षण भी करता है। इन्हें बाद में विंडोज़ के tf.data.Dataset s में बदल दिया जाएगा।
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
इस खंड की शुरुआत में आरेखों में दिखाए गए 2 विंडो बनाने के लिए कोड यहां दिया गया है:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. विभाजित
लगातार इनपुट की सूची को देखते हुए, split_window विधि उन्हें इनपुट की एक विंडो और लेबल की एक विंडो में बदल देगी।
उदाहरण w2 जिसे आप पहले परिभाषित करते हैं, इस तरह विभाजित किया जाएगा:

यह आरेख डेटा की features अक्ष नहीं दिखाता है, लेकिन यह split_window फ़ंक्शन label_columns को भी संभालता है, इसलिए इसका उपयोग एकल आउटपुट और बहु-आउटपुट दोनों उदाहरणों के लिए किया जा सकता है।
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
कोशिश करके देखो:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
आमतौर पर, TensorFlow में डेटा को सरणियों में पैक किया जाता है, जहां सबसे बाहरी सूचकांक उदाहरणों ("बैच" आयाम) में होता है। मध्य सूचकांक "समय" या "स्थान" (चौड़ाई, ऊंचाई) आयाम हैं। अंतरतम सूचकांक विशेषताएं हैं।
ऊपर दिए गए कोड ने प्रत्येक समय चरण में 19 सुविधाओं के साथ तीन 7-बार चरण वाली विंडो का एक बैच लिया। यह उन्हें 6-बार चरण 19-सुविधा इनपुट के एक बैच और 1-बार चरण 1-फ़ीचर लेबल में विभाजित करता है। लेबल में केवल एक विशेषता है क्योंकि WindowGenerator को label_columns=['T (degC)'] साथ प्रारंभ किया गया था। प्रारंभ में, यह ट्यूटोरियल ऐसे मॉडल बनाएगा जो एकल आउटपुट लेबल की भविष्यवाणी करते हैं।
3. प्लॉट
यहाँ एक प्लॉट विधि है जो स्प्लिट विंडो के एक सरल दृश्य की अनुमति देती है:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
यह प्लॉट उस समय के आधार पर इनपुट, लेबल और (बाद में) भविष्यवाणियों को संरेखित करता है जो आइटम को संदर्भित करता है:
w2.plot()
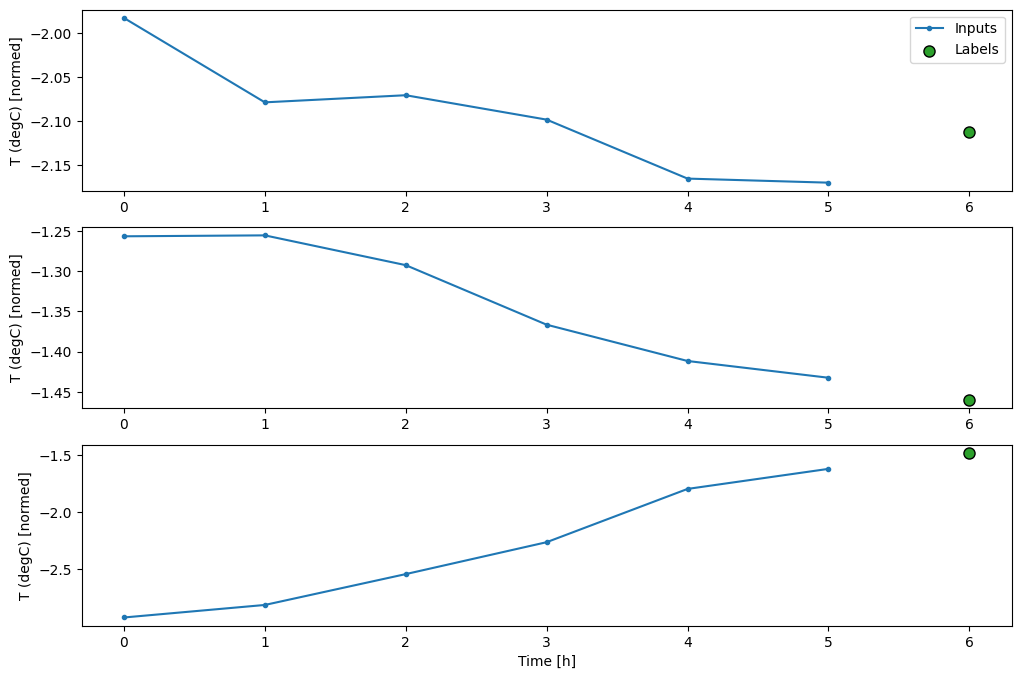
आप अन्य कॉलम प्लॉट कर सकते हैं, लेकिन उदाहरण विंडो w2 कॉन्फ़िगरेशन में केवल T (degC) कॉलम के लिए लेबल हैं।
w2.plot(plot_col='p (mbar)')
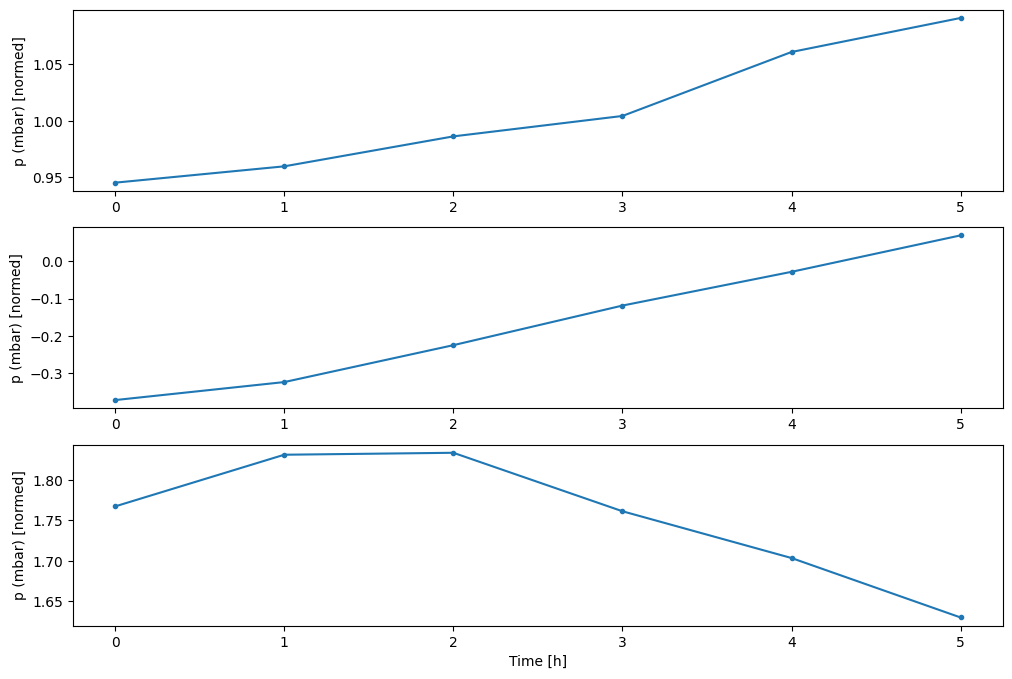
4. tf.data.Dataset s . बनाएं
अंत में, यह make_dataset विधि एक समय श्रृंखला डेटाफ़्रेम लेगी और इसे tf.data.Dataset . (input_window, label_window) जोड़े में tf.keras.utils.timeseries_dataset_from_array फ़ंक्शन का उपयोग करके परिवर्तित करेगी:
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
WindowGenerator ऑब्जेक्ट में प्रशिक्षण, सत्यापन और परीक्षण डेटा होता है।
आपके द्वारा पहले परिभाषित की गई make_dataset पद्धति का उपयोग करके उन्हें tf.data.Dataset s के रूप में एक्सेस करने के लिए गुण जोड़ें। साथ ही, आसान पहुंच और प्लॉटिंग के लिए एक मानक उदाहरण बैच जोड़ें:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
अब, WindowGenerator ऑब्जेक्ट आपको tf.data.Dataset ऑब्जेक्ट तक पहुंच प्रदान करता है, ताकि आप डेटा पर आसानी से पुनरावृति कर सकें।
Dataset.element_spec गुण आपको डेटासेट तत्वों की संरचना, डेटा प्रकार और आकार बताता है।
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
Dataset पर पुनरावृति करने से ठोस बैच प्राप्त होते हैं:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
सिंगल स्टेप मॉडल
इस प्रकार के डेटा पर आप जो सबसे सरल मॉडल बना सकते हैं, वह वह है जो केवल वर्तमान परिस्थितियों के आधार पर किसी एकल विशेषता के मान—1 समय चरण (एक घंटा) को भविष्य में भविष्यवाणी करता है।
तो, भविष्य में एक घंटे के T (degC) मूल्य की भविष्यवाणी करने के लिए मॉडल बनाकर शुरू करें।
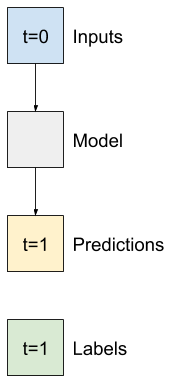
इन सिंगल-स्टेप (input, label) जोड़े को बनाने के लिए WindowGenerator ऑब्जेक्ट को कॉन्फ़िगर करें:
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
window ऑब्जेक्ट प्रशिक्षण, सत्यापन और परीक्षण सेट से tf.data.Dataset बनाता है, जिससे आप डेटा के बैचों पर आसानी से पुनरावृति कर सकते हैं।
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
आधारभूत
एक प्रशिक्षित मॉडल बनाने से पहले बाद के अधिक जटिल मॉडल के साथ तुलना करने के लिए एक बिंदु के रूप में एक प्रदर्शन आधार रेखा होना अच्छा होगा।
सभी सुविधाओं के वर्तमान मूल्य को देखते हुए, यह पहला कार्य भविष्य में एक घंटे के तापमान की भविष्यवाणी करना है। वर्तमान मूल्यों में वर्तमान तापमान शामिल है।
तो, एक मॉडल के साथ शुरू करें जो "कोई परिवर्तन नहीं" की भविष्यवाणी करते हुए, वर्तमान तापमान को भविष्यवाणी के रूप में लौटाता है। यह एक उचित आधार रेखा है क्योंकि तापमान धीरे-धीरे बदलता है। बेशक, अगर आप भविष्य में और भविष्यवाणी करते हैं तो यह आधार रेखा कम काम करेगी।
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
इस मॉडल को तत्काल और मूल्यांकन करें:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
इसने कुछ प्रदर्शन मेट्रिक्स मुद्रित किए, लेकिन वे आपको यह महसूस नहीं कराते कि मॉडल कितना अच्छा कर रहा है।
WindowGenerator में एक प्लॉट विधि है, लेकिन प्लॉट केवल एक नमूने के साथ बहुत दिलचस्प नहीं होंगे।
तो, एक व्यापक विंडो WindowGenerator बनाएं जो एक बार में लगातार 24 घंटे के इनपुट और लेबल के लिए विंडोज़ उत्पन्न करता है। नया wide_window वेरिएबल मॉडल के संचालन के तरीके को नहीं बदलता है। मॉडल अभी भी एक इनपुट समय चरण के आधार पर भविष्य में एक घंटे की भविष्यवाणी करता है। यहां, time अक्ष batch अक्ष की तरह कार्य करता है: प्रत्येक भविष्यवाणी स्वतंत्र रूप से समय चरणों के बीच कोई बातचीत नहीं की जाती है:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
इस विस्तारित विंडो को बिना किसी कोड परिवर्तन के सीधे उसी baseline मॉडल में पास किया जा सकता है। यह संभव है क्योंकि इनपुट और लेबल में समान समय के चरण होते हैं, और बेसलाइन केवल इनपुट को आउटपुट में अग्रेषित करता है:

print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
बेसलाइन मॉडल की भविष्यवाणियों की साजिश रचकर, ध्यान दें कि यह केवल एक घंटे में लेबल को स्थानांतरित कर दिया गया है:
wide_window.plot(baseline)
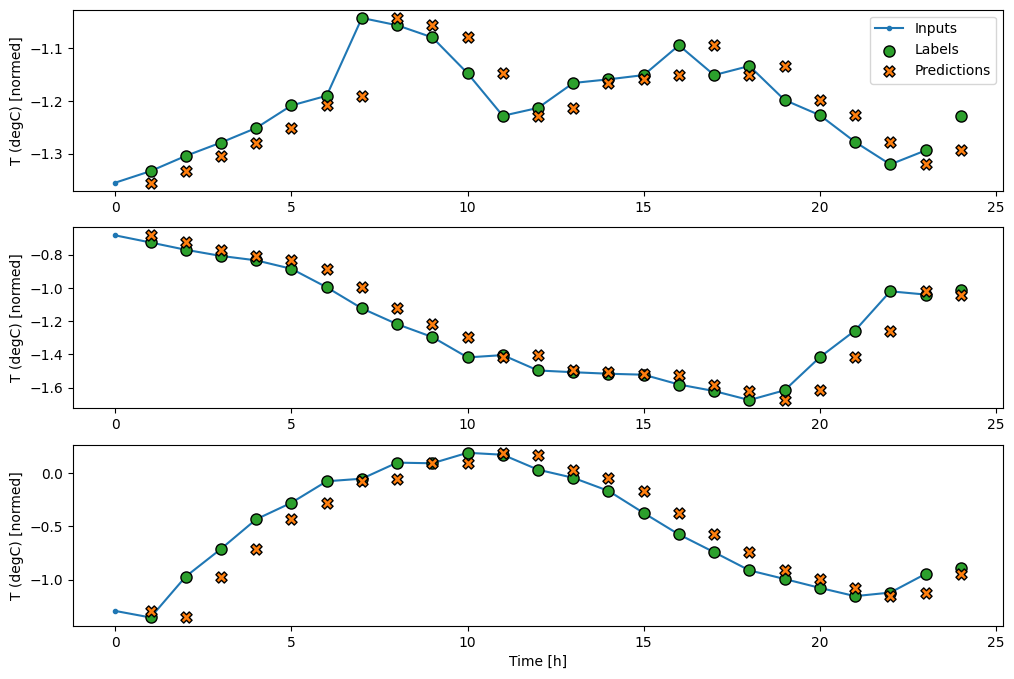
तीन उदाहरणों के उपरोक्त भूखंडों में 24 घंटे के दौरान सिंगल स्टेप मॉडल चलाया जाता है। यह कुछ स्पष्टीकरण के योग्य है:
- नीली
Inputsलाइन हर समय कदम पर इनपुट तापमान दिखाती है। मॉडल सभी सुविधाओं को प्राप्त करता है, यह प्लॉट केवल तापमान दिखाता है। - हरे रंग के
Labelsबिंदु लक्ष्य पूर्वानुमान मान दिखाते हैं। इन बिंदुओं को भविष्यवाणी समय पर दिखाया जाता है, इनपुट समय पर नहीं। यही कारण है कि लेबल की श्रेणी को इनपुट के सापेक्ष 1 कदम स्थानांतरित कर दिया जाता है। - ऑरेंज
Predictionsक्रॉस प्रत्येक आउटपुट टाइम स्टेप के लिए मॉडल की भविष्यवाणी है। यदि मॉडल पूरी तरह से भविष्यवाणी कर रहे थे तो भविष्यवाणियां सीधेLabelsपर आ जाएंगी।
रैखिक मॉडल
इस कार्य के लिए आप सबसे सरल प्रशिक्षण योग्य मॉडल लागू कर सकते हैं जो इनपुट और आउटपुट के बीच रैखिक परिवर्तन सम्मिलित करना है। इस मामले में एक समय चरण से आउटपुट केवल उस चरण पर निर्भर करता है:

एक tf.keras.layers.Dense परत जिसमें कोई activation सेट नहीं है एक रैखिक मॉडल है। परत केवल डेटा के अंतिम अक्ष को (batch, time, inputs) से (batch, time, units) बदल देती है; यह batch और time अक्षों में प्रत्येक आइटम पर स्वतंत्र रूप से लागू होता है।
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
यह ट्यूटोरियल कई मॉडलों को प्रशिक्षित करता है, इसलिए प्रशिक्षण प्रक्रिया को एक फ़ंक्शन में पैकेज करें:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
मॉडल को प्रशिक्षित करें और उसके प्रदर्शन का मूल्यांकन करें:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
baseline मॉडल की तरह, लीनियर मॉडल को विस्तृत विंडो के बैच पर कॉल किया जा सकता है। इस तरह इस्तेमाल किया गया मॉडल लगातार समय के चरणों पर स्वतंत्र भविष्यवाणियों का एक सेट बनाता है। time अक्ष दूसरे batch अक्ष की तरह कार्य करता है। हर समय कदम पर भविष्यवाणियों के बीच कोई बातचीत नहीं होती है।

print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
यहाँ इसके उदाहरण की भविष्यवाणी की साजिश है wide_window , ध्यान दें कि कितने मामलों में भविष्यवाणी केवल इनपुट तापमान को वापस करने से बेहतर है, लेकिन कुछ मामलों में यह बदतर है:
wide_window.plot(linear)
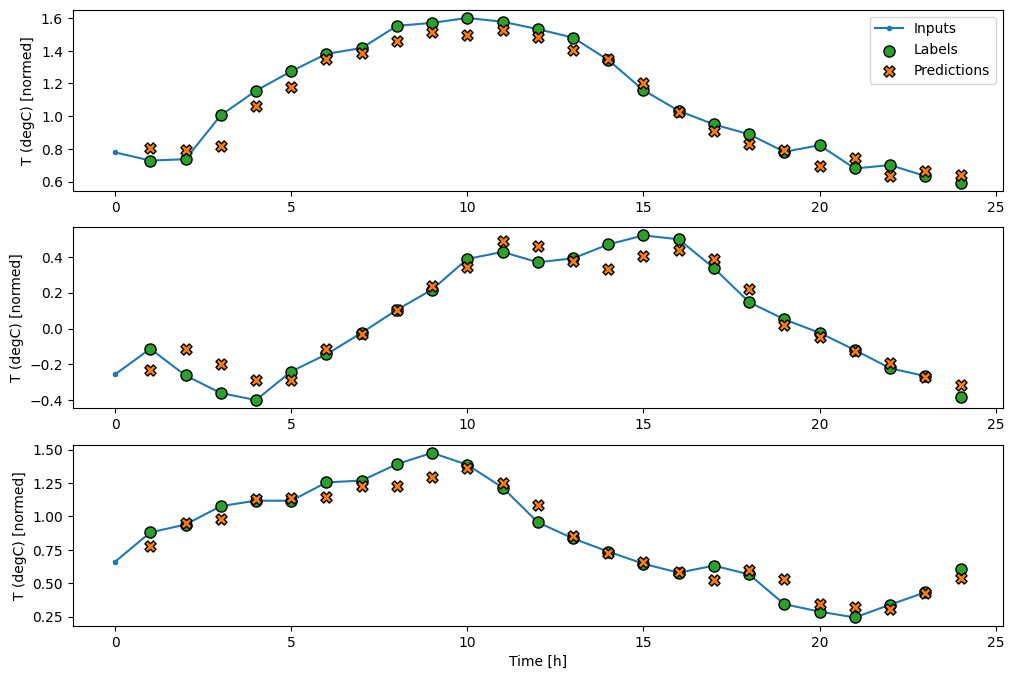
रैखिक मॉडल का एक फायदा यह है कि वे व्याख्या करने के लिए अपेक्षाकृत सरल हैं। आप परत के भार को बाहर निकाल सकते हैं और प्रत्येक इनपुट को दिए गए भार की कल्पना कर सकते हैं:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)

कभी-कभी मॉडल इनपुट T (degC) पर सबसे अधिक भार भी नहीं डालता है। यह यादृच्छिक आरंभीकरण के जोखिमों में से एक है।
सघन
ऐसे मॉडल लागू करने से पहले जो वास्तव में कई समय-चरणों पर काम करते हैं, यह गहन, अधिक शक्तिशाली, एकल इनपुट चरण मॉडल के प्रदर्शन की जाँच करने योग्य है।
यहां linear मॉडल के समान एक मॉडल है, सिवाय इसके कि यह इनपुट और आउटपुट के बीच कई Dense परतों को ढेर करता है:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
बहु-चरण घना
एक सिंगल-टाइम-स्टेप मॉडल में इसके इनपुट के वर्तमान मूल्यों के लिए कोई संदर्भ नहीं है। यह नहीं देख सकता कि समय के साथ इनपुट सुविधाएँ कैसे बदल रही हैं। इस समस्या को हल करने के लिए मॉडल को भविष्यवाणी करते समय कई समय के चरणों तक पहुंच की आवश्यकता होती है:

baseline , linear और dense मॉडल हर बार स्टेप को स्वतंत्र रूप से हैंडल करते हैं। यहां मॉडल एकल आउटपुट का उत्पादन करने के लिए इनपुट के रूप में कई बार कदम उठाएगा।
एक WindowGenerator बनाएं जो तीन घंटे के इनपुट और एक घंटे के लेबल के बैच तैयार करेगा:
ध्यान दें कि Window का shift पैरामीटर दो विंडो के अंत के सापेक्ष है।
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
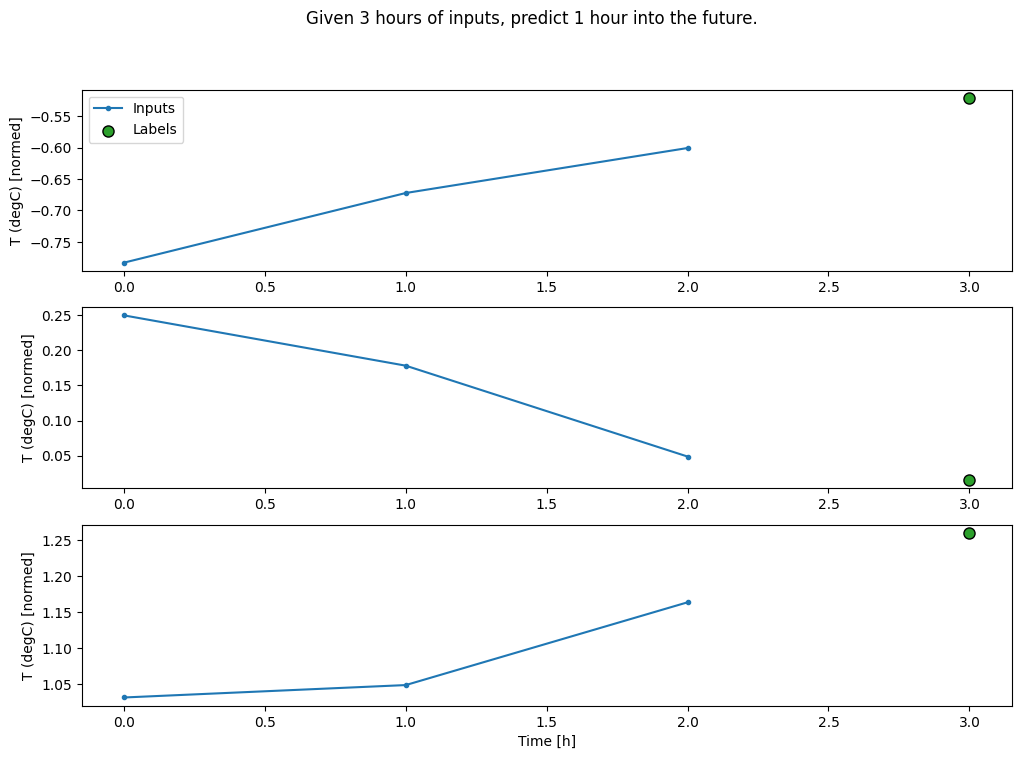
आप tf.keras.layers.Flatten को मॉडल की पहली परत के रूप में जोड़कर बहु-इनपुट-चरण विंडो पर एक dense मॉडल को प्रशिक्षित कर सकते हैं:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
conv_window.plot(multi_step_dense)
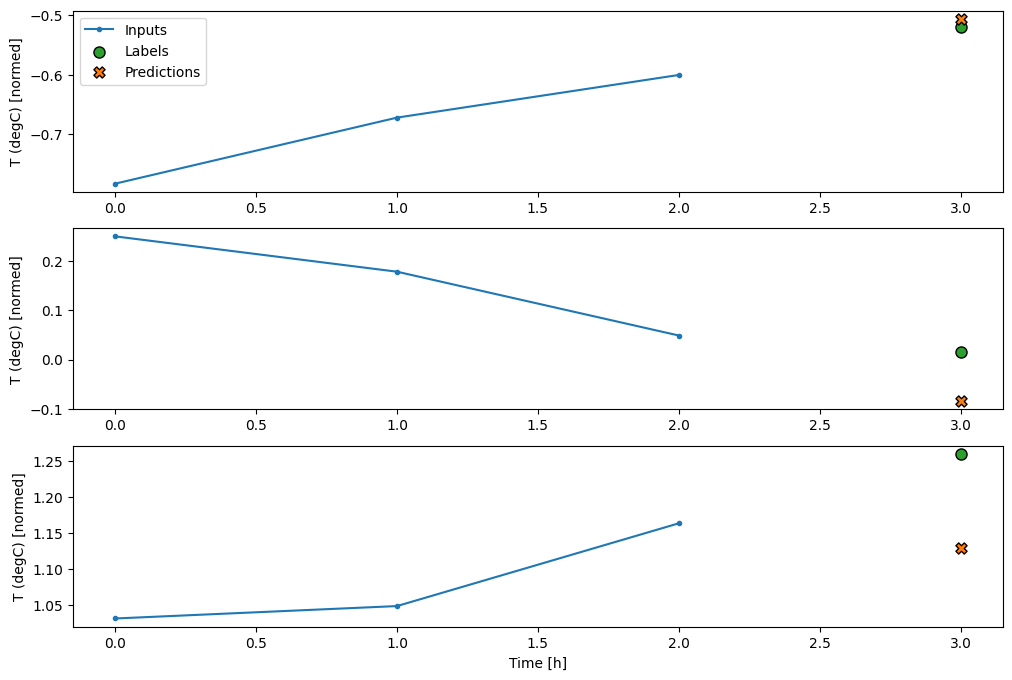
इस दृष्टिकोण का मुख्य नकारात्मक पक्ष यह है कि परिणामी मॉडल को केवल इस आकार की इनपुट विंडो पर ही निष्पादित किया जा सकता है।
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
अगले भाग में संकेंद्रित मॉडल इस समस्या को ठीक करते हैं।
कनवल्शन न्यूरल नेटवर्क
एक कनवल्शन लेयर ( tf.keras.layers.Conv1D ) भी प्रत्येक भविष्यवाणी के इनपुट के रूप में कई बार कदम उठाता है।
नीचे multi_step_dense जैसा ही मॉडल है, जिसे कनवल्शन के साथ फिर से लिखा गया है।
परिवर्तनों पर ध्यान दें:
-
tf.keras.layers.Flattenऔर पहलेtf.keras.layers.Denseकोtf.keras.layers.Conv1Dद्वारा प्रतिस्थापित किया जाता है। -
tf.keras.layers.Reshapeअब आवश्यक नहीं है क्योंकि कनवल्शन अपने आउटपुट में समय अक्ष रखता है।
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
यह जांचने के लिए एक उदाहरण बैच पर चलाएँ कि मॉडल अपेक्षित आकार के साथ आउटपुट उत्पन्न करता है:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
इसे conv_window पर प्रशिक्षित करें और इसका मूल्यांकन करें और इसे multi_step_dense मॉडल के समान प्रदर्शन देना चाहिए।
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
इस conv_model और multi_step_dense मॉडल के बीच का अंतर यह है कि conv_model को किसी भी लम्बाई के इनपुट पर चलाया जा सकता है। इनपुट की स्लाइडिंग विंडो पर कनवल्शनल लेयर लागू होती है:

यदि आप इसे व्यापक इनपुट पर चलाते हैं, तो यह व्यापक आउटपुट उत्पन्न करता है:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
ध्यान दें कि आउटपुट इनपुट से छोटा है। प्रशिक्षण या साजिश रचने का काम करने के लिए, आपको समान लंबाई के लेबल और भविष्यवाणी की आवश्यकता होती है। इसलिए कुछ अतिरिक्त इनपुट समय चरणों के साथ विस्तृत विंडो बनाने के लिए WindowGenerator का निर्माण करें ताकि लेबल और भविष्यवाणी की लंबाई मेल खा सके:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
अब, आप मॉडल की भविष्यवाणियों को एक विस्तृत विंडो पर प्लॉट कर सकते हैं। पहली भविष्यवाणी से पहले 3 इनपुट समय चरणों पर ध्यान दें। यहां हर भविष्यवाणी 3 पूर्ववर्ती समय चरणों पर आधारित है:
wide_conv_window.plot(conv_model)
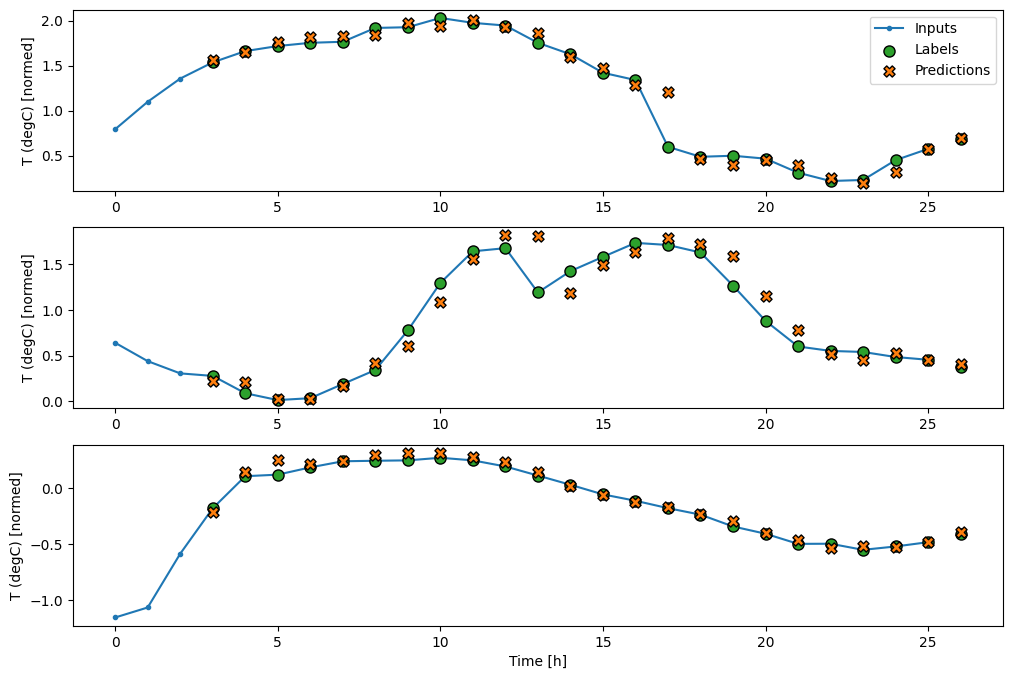
आवर्तक तंत्रिका नेटवर्क
एक आवर्तक तंत्रिका नेटवर्क (RNN) एक प्रकार का तंत्रिका नेटवर्क है जो समय श्रृंखला डेटा के लिए उपयुक्त है। आरएनएन एक समय-श्रृंखला को चरण-दर-चरण संसाधित करते हैं, समय-समय पर आंतरिक स्थिति को बनाए रखते हैं।
आप पाठ पीढ़ी में आरएनएन ट्यूटोरियल और केरस गाइड के साथ आवर्तक तंत्रिका नेटवर्क (आरएनएन) के साथ अधिक सीख सकते हैं।
इस ट्यूटोरियल में, आप लॉन्ग शॉर्ट-टर्म मेमोरी ( tf.keras.layers.LSTM ) नामक RNN लेयर का उपयोग करेंगे।
सभी केरस आरएनएन परतों के लिए एक महत्वपूर्ण कंस्ट्रक्टर तर्क, जैसे कि tf.keras.layers.LSTM , है return_sequences तर्क। यह सेटिंग परत को दो में से किसी एक तरीके से कॉन्फ़िगर कर सकती है:
- यदि
Falseहै, तो डिफ़ॉल्ट, परत केवल अंतिम समय चरण का आउटपुट लौटाती है, जिससे मॉडल को एकल भविष्यवाणी करने से पहले अपनी आंतरिक स्थिति को गर्म करने का समय मिलता है:
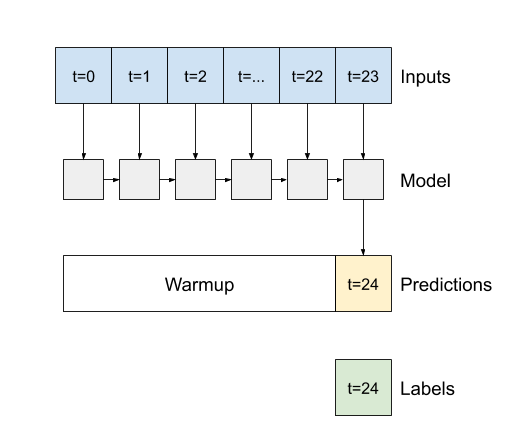
- यदि
Trueहै, तो परत प्रत्येक इनपुट के लिए एक आउटपुट लौटाती है। यह इसके लिए उपयोगी है:- आरएनएन परतों को ढेर करना।
- एक साथ कई समय के चरणों पर एक मॉडल का प्रशिक्षण।
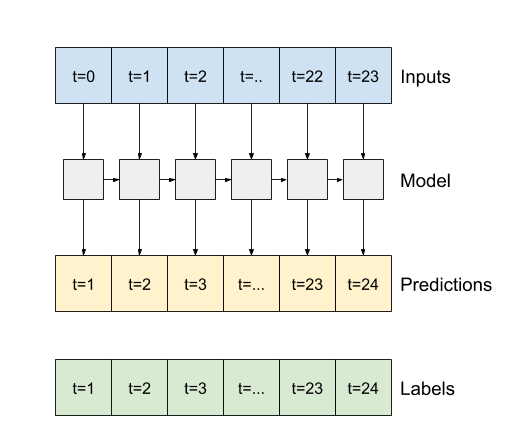
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
return_sequences=True के साथ, मॉडल को एक बार में 24 घंटे के डेटा पर प्रशिक्षित किया जा सकता है।
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
wide_window.plot(lstm_model)
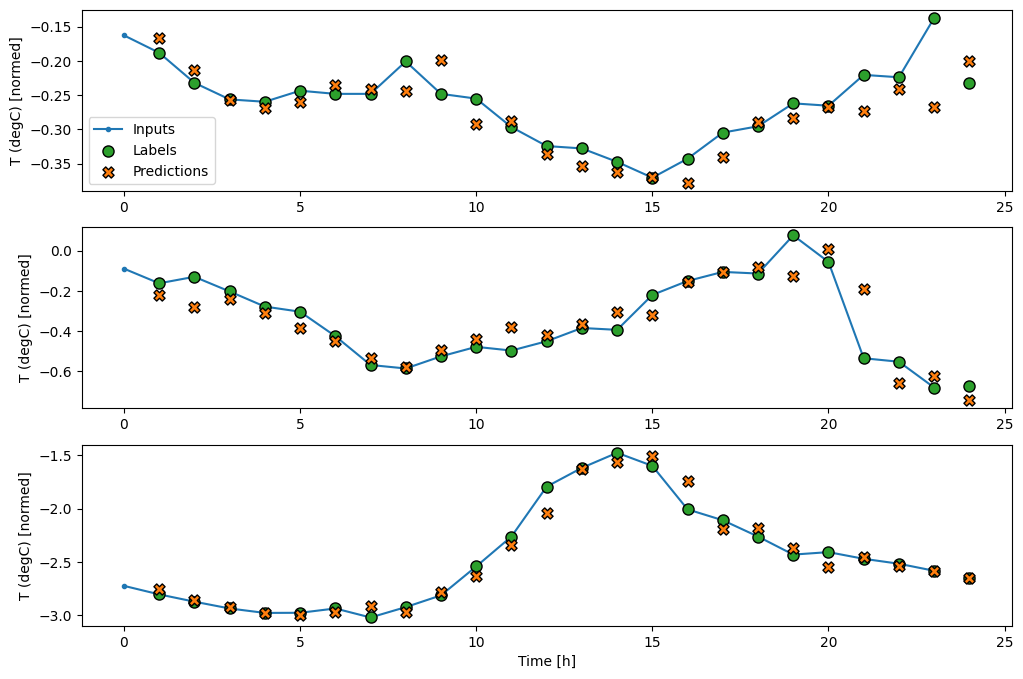
प्रदर्शन
इस डेटासेट के साथ आमतौर पर प्रत्येक मॉडल पहले वाले की तुलना में थोड़ा बेहतर करता है:
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()

for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
मल्टी-आउटपुट मॉडल
अब तक के सभी मॉडलों ने सिंगल आउटपुट फीचर, T (degC) की भविष्यवाणी सिंगल टाइम स्टेप के लिए की थी।
इन सभी मॉडलों को केवल आउटपुट परत में इकाइयों की संख्या को बदलकर और labels में सभी सुविधाओं को शामिल करने के लिए प्रशिक्षण विंडो को समायोजित करके कई विशेषताओं की भविष्यवाणी करने के लिए परिवर्तित किया जा सकता है ( example_labels ):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
ऊपर ध्यान दें कि लेबल के features अक्ष में अब 1 के बजाय इनपुट के समान गहराई है।
आधारभूत
यहां एक ही बेसलाइन मॉडल ( Baseline ) का उपयोग किया जा सकता है, लेकिन इस बार एक विशिष्ट label_index चुनने के बजाय सभी सुविधाओं को दोहराते हुए:
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
सघन
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
आरएनएन
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
उन्नत: अवशिष्ट कनेक्शन
पहले के Baseline मॉडल ने इस तथ्य का लाभ उठाया कि अनुक्रम समय-समय पर चरण-दर-चरण में अत्यधिक परिवर्तन नहीं करता है। इस ट्यूटोरियल में अब तक प्रशिक्षित प्रत्येक मॉडल को बेतरतीब ढंग से इनिशियलाइज़ किया गया था, और फिर यह सीखना था कि आउटपुट पिछले समय के चरण से एक छोटा बदलाव है।
जब आप सावधानीपूर्वक आरंभीकरण के साथ इस मुद्दे को हल कर सकते हैं, तो इसे मॉडल संरचना में बनाना आसान है।
मॉडल बनाने के लिए समय श्रृंखला विश्लेषण में यह सामान्य है कि अगले मूल्य की भविष्यवाणी करने के बजाय, भविष्यवाणी करें कि अगली बार चरण में मूल्य कैसे बदलेगा। इसी तरह, अवशिष्ट नेटवर्क -या ResNets- गहन शिक्षण में आर्किटेक्चर को संदर्भित करता है जहां प्रत्येक परत मॉडल के संचय परिणाम में जोड़ती है।
इस तरह आप इस ज्ञान का लाभ उठाते हैं कि परिवर्तन छोटा होना चाहिए।

अनिवार्य रूप से, यह Baseline से मेल खाने के लिए मॉडल को इनिशियलाइज़ करता है। इस कार्य के लिए यह मॉडल को थोड़ा बेहतर प्रदर्शन के साथ तेजी से अभिसरण करने में मदद करता है।
इस ट्यूटोरियल में चर्चा किए गए किसी भी मॉडल के संयोजन के साथ इस दृष्टिकोण का उपयोग किया जा सकता है।
यहां, इसे LSTM मॉडल पर लागू किया जा रहा है, यह सुनिश्चित करने के लिए tf.initializers.zeros के उपयोग पर ध्यान दें कि प्रारंभिक पूर्वानुमानित परिवर्तन छोटे हैं, और अवशिष्ट कनेक्शन को प्रबल नहीं करते हैं। यहां ग्रेडिएंट के लिए कोई समरूपता-तोड़ने वाली चिंता नहीं है, क्योंकि zeros का उपयोग केवल अंतिम परत पर किया जाता है।
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
प्रदर्शन
इन बहु-आउटपुट मॉडलों के लिए समग्र प्रदर्शन यहां दिया गया है।
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
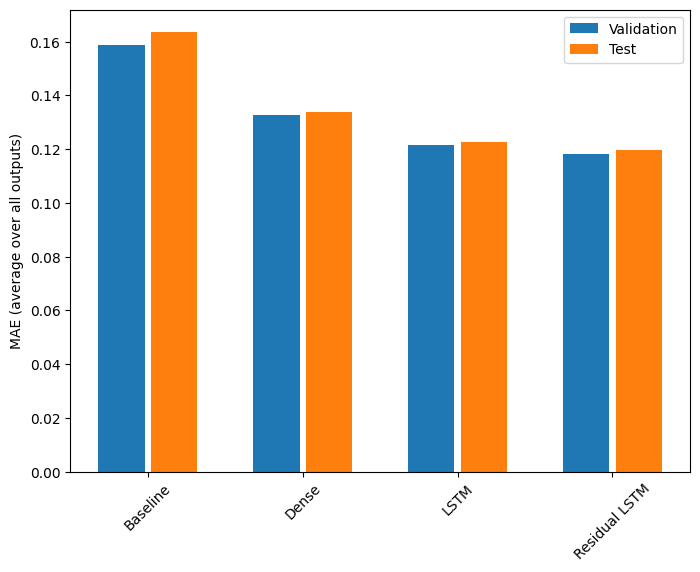
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
उपरोक्त प्रदर्शन सभी मॉडल आउटपुट में औसत हैं।
बहु-चरण मॉडल
पिछले अनुभागों में सिंगल-आउटपुट और मल्टीपल-आउटपुट मॉडल दोनों ने भविष्य में एक घंटे के लिए सिंगल टाइम स्टेप भविष्यवाणियां कीं।
यह खंड देखता है कि इन मॉडलों का विस्तार कैसे किया जाए ताकि कई बार कदम भविष्यवाणियां की जा सकें।
बहु-चरणीय भविष्यवाणी में, मॉडल को भविष्य के मूल्यों की एक श्रृंखला की भविष्यवाणी करना सीखना होगा। इस प्रकार, एकल चरण मॉडल के विपरीत, जहां केवल एक भविष्य बिंदु की भविष्यवाणी की जाती है, एक बहु-चरण मॉडल भविष्य के मूल्यों के अनुक्रम की भविष्यवाणी करता है।
इसके लिए दो मोटे दृष्टिकोण हैं:
- सिंगल शॉट भविष्यवाणियां जहां पूरी समय श्रृंखला की भविष्यवाणी एक ही बार में की जाती है।
- ऑटोरेग्रेसिव भविष्यवाणियां जहां मॉडल केवल एकल चरण भविष्यवाणियां करता है और इसके आउटपुट को इसके इनपुट के रूप में वापस फीड किया जाता है।
इस खंड में सभी मॉडल सभी आउटपुट समय चरणों में सभी सुविधाओं की भविष्यवाणी करेंगे।
मल्टी-स्टेप मॉडल के लिए, प्रशिक्षण डेटा में फिर से प्रति घंटा नमूने होते हैं। हालांकि, यहां, मॉडल 24 घंटे अतीत को देखते हुए, भविष्य में 24 घंटे की भविष्यवाणी करना सीखेंगे।
यहां एक Window ऑब्जेक्ट है जो इन स्लाइस को डेटासेट से उत्पन्न करता है:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
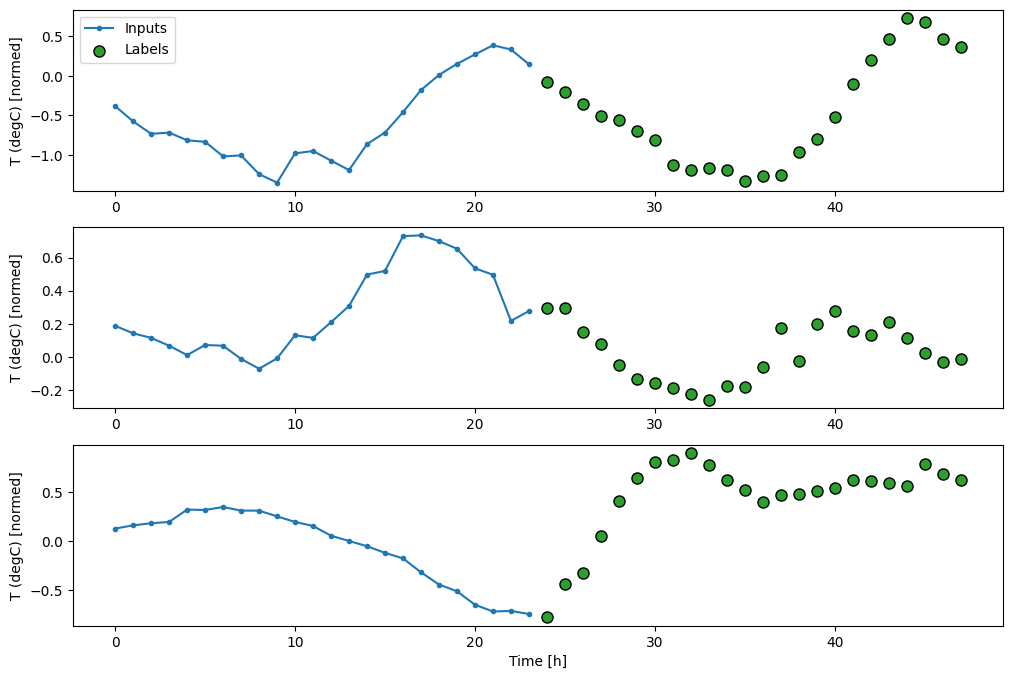
आधार रेखा
इस कार्य के लिए एक सरल आधार रेखा आउटपुट समय चरणों की आवश्यक संख्या के लिए अंतिम इनपुट समय चरण को दोहराना है:

class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007

चूंकि यह कार्य भविष्य में 24 घंटे की भविष्यवाणी करना है, पिछले 24 घंटों को देखते हुए, एक और आसान तरीका पिछले दिन को दोहराना है, यह मानते हुए कि कल समान होगा:
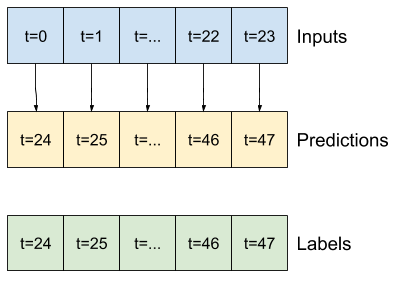
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
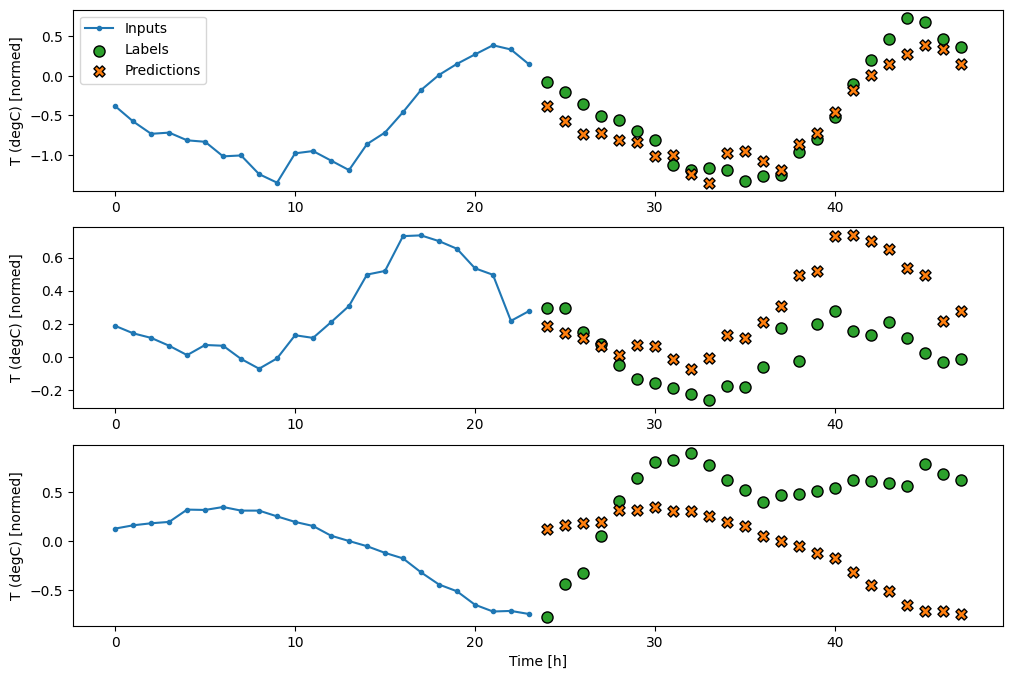
सिंगल-शॉट मॉडल
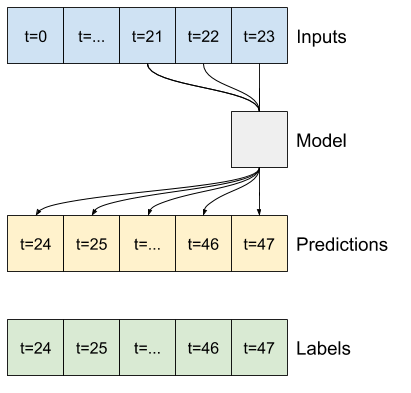
इस समस्या के लिए एक उच्च-स्तरीय दृष्टिकोण "सिंगल-शॉट" मॉडल का उपयोग करना है, जहां मॉडल एक ही चरण में पूरे अनुक्रम की भविष्यवाणी करता है।
इसे एक tf.keras.layers.Dense के रूप में कुशलतापूर्वक कार्यान्वित किया जा सकता है जिसमें OUT_STEPS*features आउटपुट यूनिट हैं। मॉडल को बस उस आउटपुट को आवश्यक (OUTPUT_STEPS, features) की जरूरत है।
रैखिक
अंतिम इनपुट समय चरण के आधार पर एक साधारण रैखिक मॉडल बेसलाइन से बेहतर करता है, लेकिन कम शक्ति वाला होता है। मॉडल को रेखीय प्रक्षेपण के साथ एकल इनपुट समय चरण से OUTPUT_STEPS समय चरणों की भविष्यवाणी करने की आवश्यकता है। यह केवल व्यवहार का एक निम्न-आयामी टुकड़ा कैप्चर कर सकता है, संभवतः मुख्य रूप से दिन के समय और वर्ष के समय पर आधारित होता है।
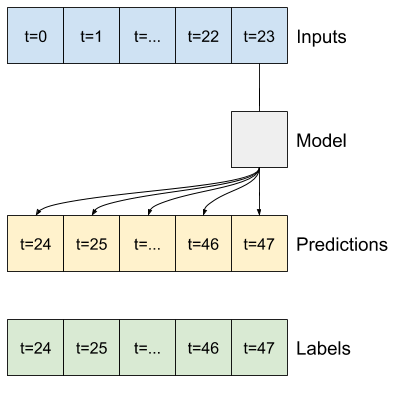
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053
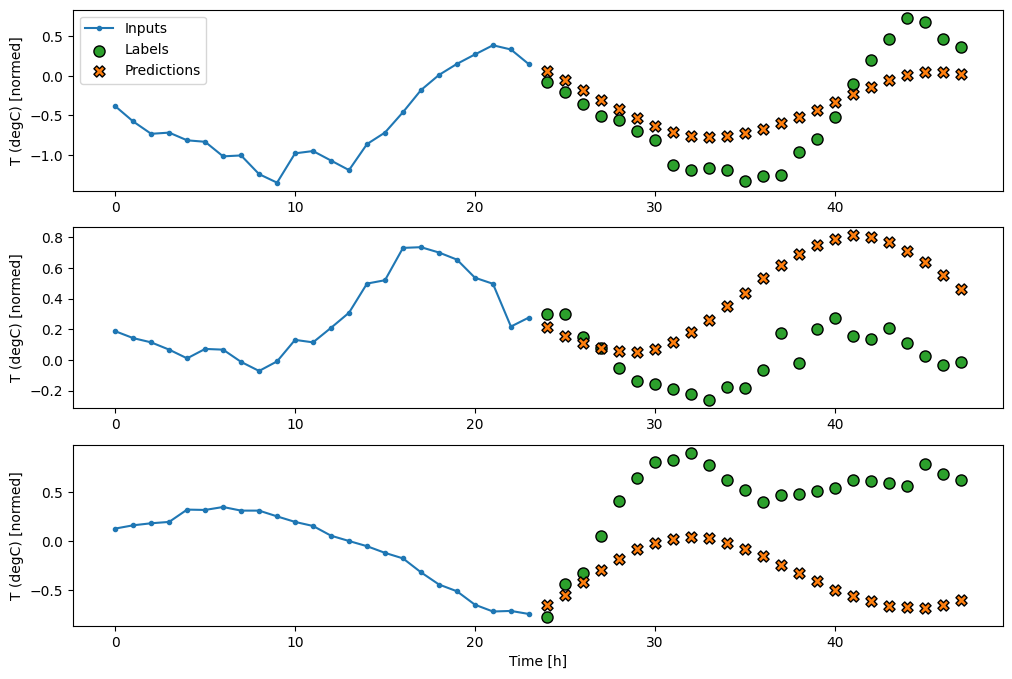
सघन
tf.keras.layers.Dense को इनपुट और आउटपुट के बीच जोड़ने से रैखिक मॉडल को अधिक शक्ति मिलती है, लेकिन यह अभी भी केवल एक इनपुट समय चरण पर आधारित है।
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
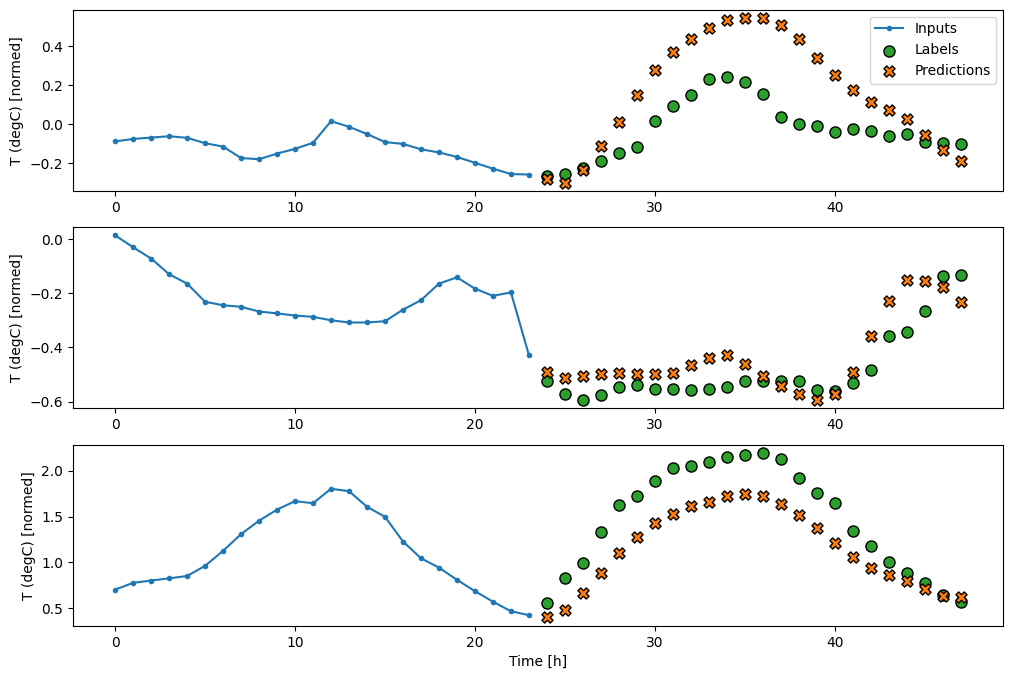
सीएनएन
एक दृढ़ मॉडल एक निश्चित-चौड़ाई वाले इतिहास के आधार पर भविष्यवाणियां करता है, जिससे घने मॉडल की तुलना में बेहतर प्रदर्शन हो सकता है क्योंकि यह देख सकता है कि समय के साथ चीजें कैसे बदल रही हैं:
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
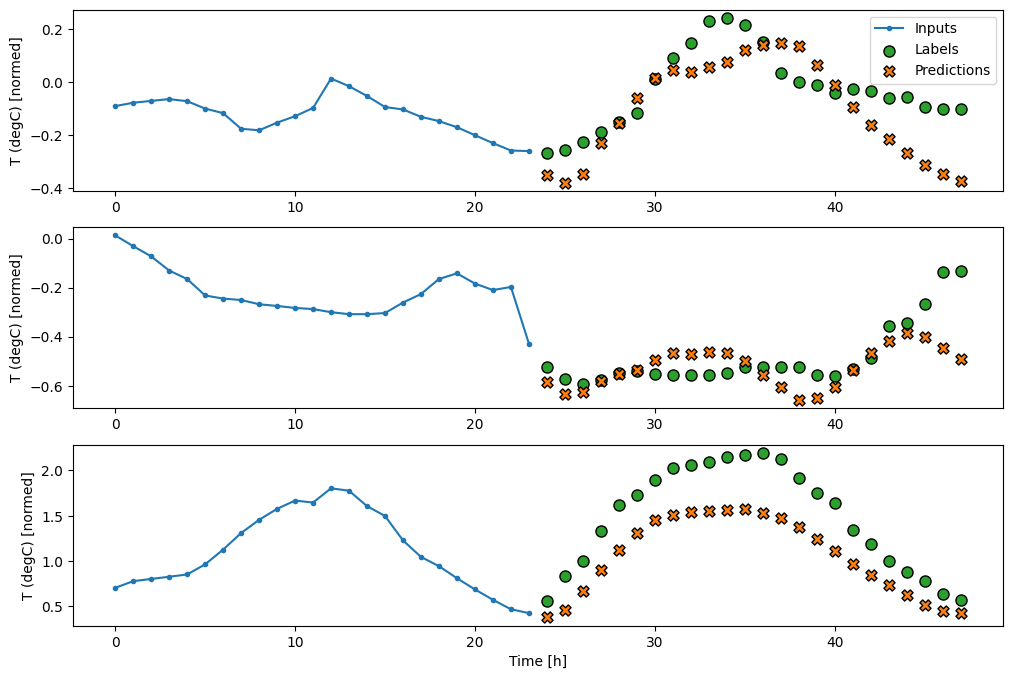
आरएनएन
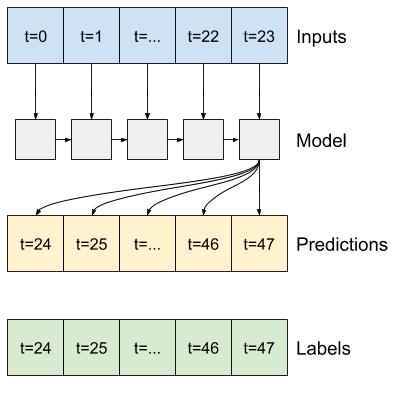
एक आवर्तक मॉडल इनपुट के लंबे इतिहास का उपयोग करना सीख सकता है, यदि यह मॉडल द्वारा की जा रही भविष्यवाणियों के लिए प्रासंगिक है। यहां अगले 24 घंटों के लिए एक भी भविष्यवाणी करने से पहले, मॉडल 24 घंटों के लिए आंतरिक स्थिति जमा करेगा।
इस सिंगल-शॉट प्रारूप में, LSTM को केवल अंतिम समय चरण में एक आउटपुट तैयार करने की आवश्यकता होती है, इसलिए tf.keras.layers.LSTM में tf.keras.layers.LSTM return_sequences=False सेट करें।
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
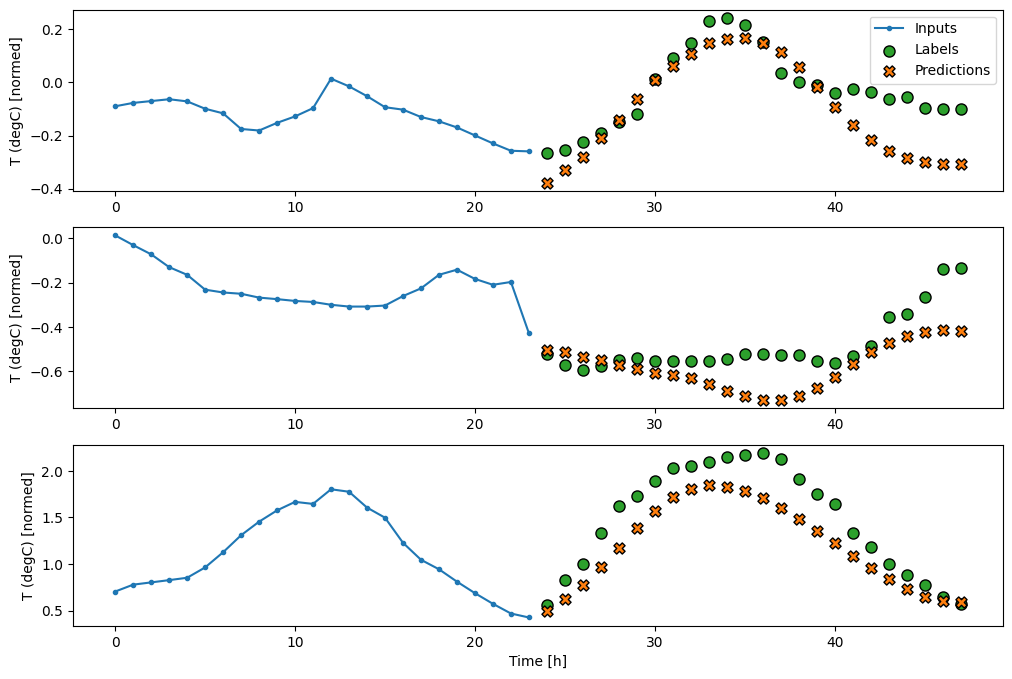
उन्नत: ऑटोरेग्रेसिव मॉडल
उपरोक्त सभी मॉडल एक ही चरण में संपूर्ण आउटपुट अनुक्रम की भविष्यवाणी करते हैं।
कुछ मामलों में यह मॉडल के लिए इस भविष्यवाणी को अलग-अलग समय चरणों में विघटित करने में मददगार हो सकता है। फिर, प्रत्येक मॉडल के आउटपुट को प्रत्येक चरण में अपने आप में वापस फीड किया जा सकता है और भविष्यवाणियों को पिछले एक पर वातानुकूलित किया जा सकता है, जैसे क्लासिक जनरेटिंग सीक्वेंस विद आवर्तक तंत्रिका नेटवर्क में।
मॉडल की इस शैली का एक स्पष्ट लाभ यह है कि इसे अलग-अलग लंबाई के साथ आउटपुट का उत्पादन करने के लिए स्थापित किया जा सकता है।
आप इस ट्यूटोरियल के पहले भाग में प्रशिक्षित सिंगल-स्टेप मल्टी-आउटपुट मॉडल में से कोई भी ले सकते हैं और ऑटोरेग्रेसिव फीडबैक लूप में चला सकते हैं, लेकिन यहां आप एक मॉडल बनाने पर ध्यान केंद्रित करेंगे जिसे स्पष्ट रूप से ऐसा करने के लिए प्रशिक्षित किया गया है।
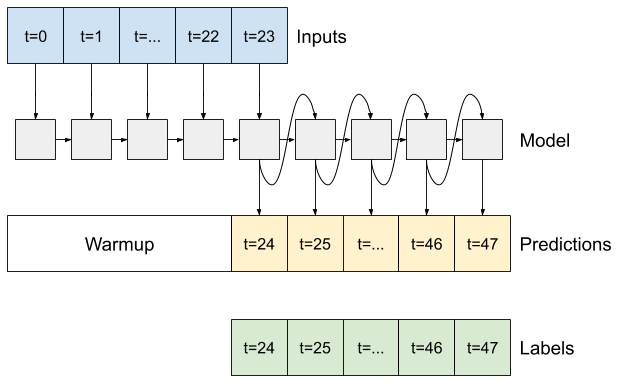
आरएनएन
यह ट्यूटोरियल केवल एक ऑटोरेग्रेसिव आरएनएन मॉडल बनाता है, लेकिन इस पैटर्न को किसी भी मॉडल पर लागू किया जा सकता है जिसे सिंगल टाइम स्टेप को आउटपुट करने के लिए डिज़ाइन किया गया था।
मॉडल का मूल रूप पहले के एकल-चरण LSTM मॉडल के समान होगा: एक tf.keras.layers.LSTM परत उसके बाद tf.keras.layers.Dense परत जो LSTM परत के आउटपुट को मॉडल भविष्यवाणियों में परिवर्तित करती है।
एक tf.keras.layers.LSTM एक tf.keras.layers.LSTMCell सेल है जो उच्च स्तर tf.keras.layers.RNN में लिपटा हुआ है जो आपके लिए स्थिति और अनुक्रम परिणामों का प्रबंधन करता है (केरस के साथ आवर्तक तंत्रिका नेटवर्क (RNN) देखें) विवरण के लिए गाइड)।
इस मामले में, मॉडल को प्रत्येक चरण के लिए इनपुट को मैन्युअल रूप से प्रबंधित करना होता है, इसलिए यह निचले स्तर, सिंगल टाइम स्टेप इंटरफ़ेस के लिए सीधे tf.keras.layers.LSTMCell का उपयोग करता है।
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
इस मॉडल को जिस पहली विधि की आवश्यकता है, वह है इनपुट के आधार पर इसकी आंतरिक स्थिति को आरंभ करने के लिए एक warmup विधि। एक बार प्रशिक्षित होने के बाद, यह राज्य इनपुट इतिहास के प्रासंगिक भागों पर कब्जा कर लेगा। यह पहले के सिंगल-स्टेप LSTM मॉडल के बराबर है:
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
यह विधि एकल समय-चरण भविष्यवाणी और LSTM की आंतरिक स्थिति लौटाती है:
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
RNN की स्थिति, और एक प्रारंभिक भविष्यवाणी के साथ, अब आप इनपुट के रूप में प्रत्येक चरण पर भविष्यवाणियों को फीड करने वाले मॉडल को पुनरावृत्त करना जारी रख सकते हैं।
आउटपुट भविष्यवाणियों को इकट्ठा करने का सबसे आसान तरीका लूप के बाद पायथन सूची और tf.stack का उपयोग करना है।
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
उदाहरण इनपुट पर इस मॉडल का परीक्षण करें:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
अब, मॉडल को प्रशिक्षित करें:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
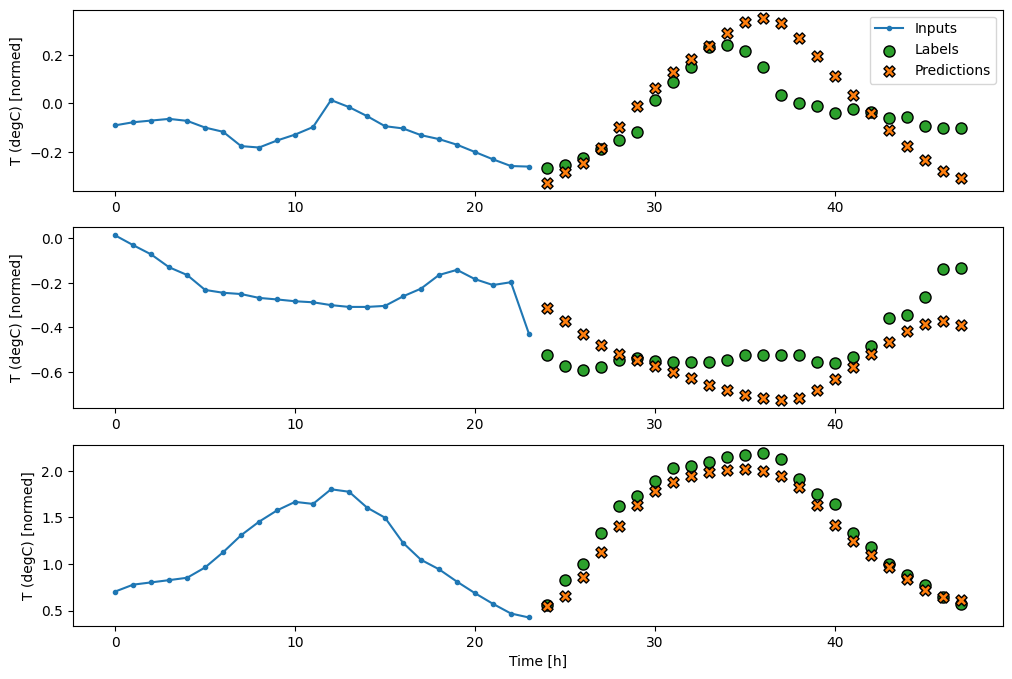
प्रदर्शन
इस समस्या पर मॉडल जटिलता के एक समारोह के रूप में स्पष्ट रूप से कम रिटर्न है:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()

इस ट्यूटोरियल की पहली छमाही में बहु-आउटपुट मॉडल के लिए मेट्रिक्स सभी आउटपुट सुविधाओं में औसत प्रदर्शन दिखाते हैं। ये प्रदर्शन समान हैं लेकिन आउटपुट समय चरणों में औसत भी हैं।
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
घने मॉडल से दृढ़ और आवर्तक मॉडल में जाने से प्राप्त लाभ केवल कुछ प्रतिशत (यदि कोई हो) हैं, और ऑटोरेग्रेसिव मॉडल ने स्पष्ट रूप से खराब प्रदर्शन किया है। तो ये अधिक जटिल दृष्टिकोण इस समस्या पर काम नहीं कर सकते हैं, लेकिन कोशिश किए बिना जानने का कोई तरीका नहीं था, और ये मॉडल आपकी समस्या के लिए सहायक हो सकते हैं।
अगले कदम
यह ट्यूटोरियल TensorFlow का उपयोग करके समय श्रृंखला पूर्वानुमान का एक त्वरित परिचय था।
अधिक जानने के लिए, देखें:
- स्किकिट-लर्न, केरस और टेंसरफ्लो के साथ हैंड्स-ऑन मशीन लर्निंग का अध्याय 15, दूसरा संस्करण।
- पायथन के साथ डीप लर्निंग का अध्याय 6।
- अभ्यास नोटबुक सहित, गहन सीखने के लिए TensorFlow में Udacity के परिचय का पाठ 8।
साथ ही, याद रखें कि आप TensorFlow में किसी भी शास्त्रीय समय श्रृंखला मॉडल को लागू कर सकते हैं—यह ट्यूटोरियल केवल TensorFlow की अंतर्निहित कार्यक्षमता पर केंद्रित है।
