 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запустить в Google Colab Запустить в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
Это руководство представляет собой введение в прогнозирование временных рядов с использованием TensorFlow. Он строит несколько разных стилей моделей, включая сверточные и рекуррентные нейронные сети (CNN и RNN).
Он состоит из двух основных частей с подразделами:
- Прогноз для одного временного шага:
- Единственная особенность.
- Все функции.
- Прогноз нескольких шагов:
- Single-shot: Делайте прогнозы сразу.
- Авторегрессия: делайте по одному прогнозу за раз и отправляйте выходные данные обратно в модель.
Настраивать
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
Набор данных о погоде
В этом руководстве используется набор данных временных рядов погоды, записанный Институтом биогеохимии Макса Планка .
Этот набор данных содержит 14 различных характеристик, таких как температура воздуха, атмосферное давление и влажность. Они собирались каждые 10 минут, начиная с 2003 года. Для эффективности вы будете использовать только данные, собранные в период с 2009 по 2016 год. Этот раздел набора данных был подготовлен Франсуа Шолле для его книги Deep Learning with Python .
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
В этом руководстве будут рассматриваться только почасовые прогнозы , поэтому начните с подвыборки данных с 10-минутных интервалов на одночасовые:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
Давайте взглянем на данные. Вот первые несколько строк:
df.head()
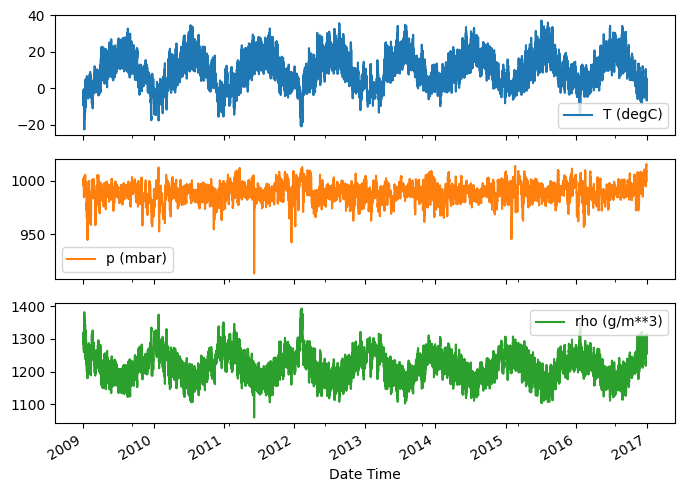
Вот эволюция некоторых функций с течением времени:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
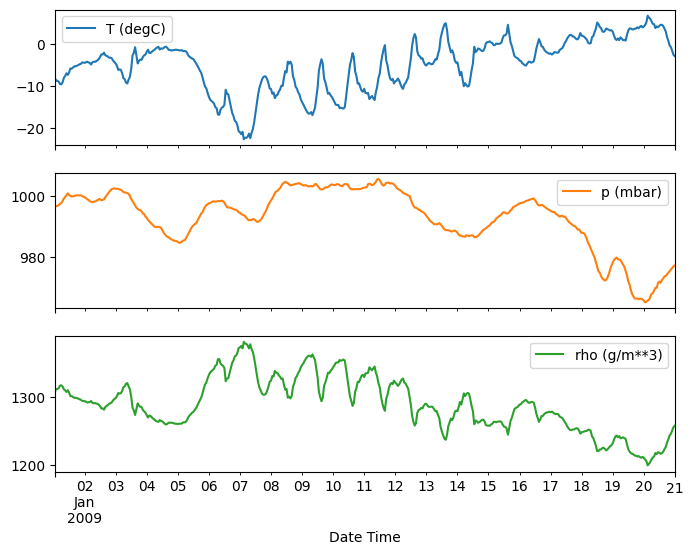
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
Осмотр и очистка
Далее посмотрим на статистику набора данных:
df.describe().transpose()
Скорость ветра
Следует выделить столбцы min значения скорости ветра ( wv (m/s) ) и максимального значения ( max. wv (m/s) ). Это -9999 , вероятно, ошибочно.
Есть отдельный столбец направления ветра, поэтому скорость должна быть больше нуля ( >=0 ). Замените его нулями:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
Разработка функций
Прежде чем погрузиться в построение модели, важно понять ваши данные и убедиться, что вы передаете модели данные в соответствующем формате.
Ветер
Последний столбец данных, wd (deg) — указывает направление ветра в градусах. Углы не подходят для ввода модели: 360° и 0° должны располагаться близко друг к другу и плавно перетекать друг в друга. Направление не имеет значения, если ветер не дует.
Сейчас распределение данных о ветре выглядит так:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
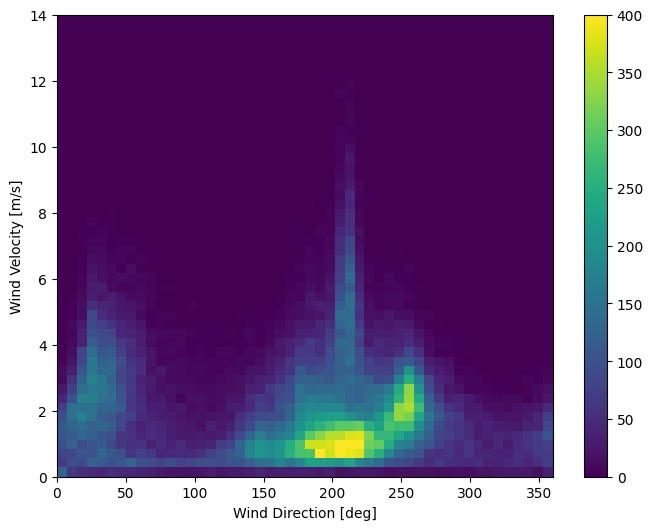
Но это будет легче интерпретировать модели, если вы преобразуете столбцы направления и скорости ветра в вектор ветра:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
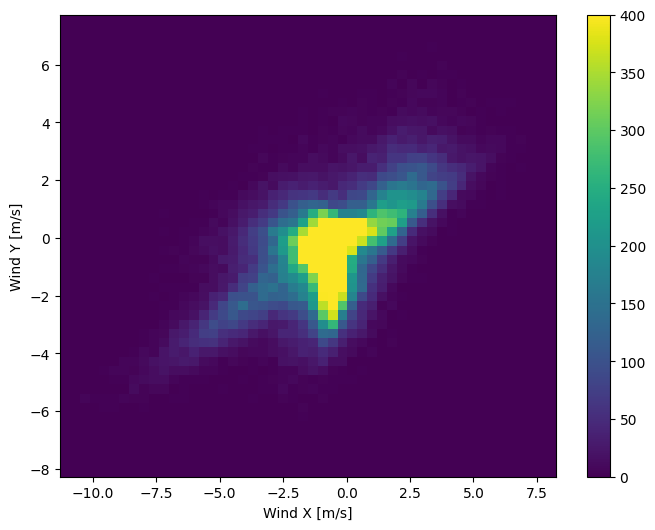
Распределение векторов ветра гораздо проще правильно интерпретировать моделью:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
Время
Точно так же столбец Date Time очень полезен, но не в этой строковой форме. Начните с преобразования его в секунды:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
Как и в случае с направлением ветра, время в секундах не является полезным входным параметром модели. Будучи данными о погоде, они имеют четкую дневную и годовую периодичность. Есть много способов справиться с периодичностью.
Вы можете получить полезные сигналы, используя синусоидальные и косинусные преобразования для очистки сигналов «Время суток» и «Время года»:
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
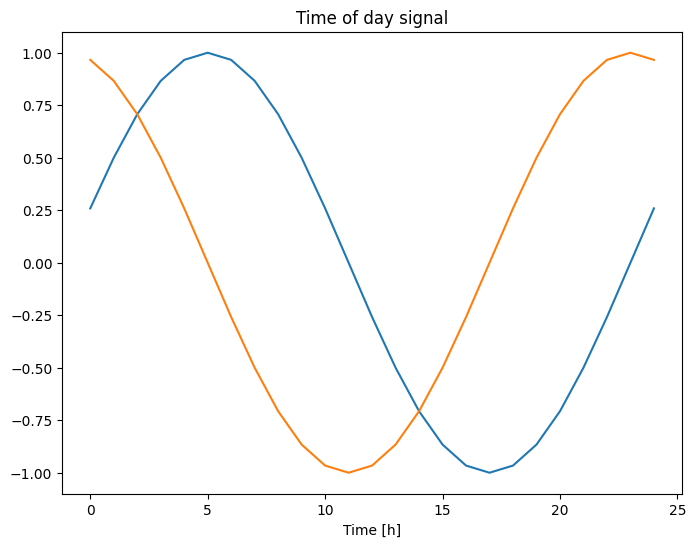
Это дает модели доступ к наиболее важным характеристикам частоты. В этом случае вы заранее знали, какие частоты важны.
Если у вас нет этой информации, вы можете определить, какие частоты важны, извлекая признаки с помощью быстрого преобразования Фурье . Чтобы проверить предположения, вот tf.signal.rfft изменения температуры во времени. Обратите внимание на очевидные пики на частотах около 1/year и 1/day :
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
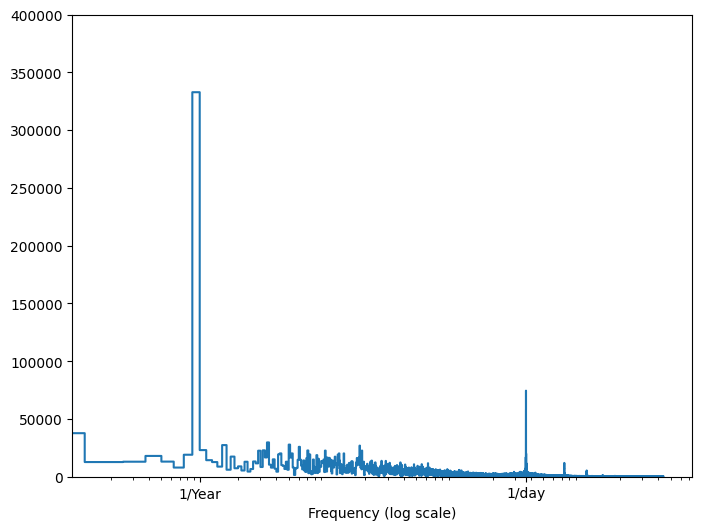
Разделить данные
Вы будете использовать разделение (70%, 20%, 10%) для обучающих, проверочных и тестовых наборов. Обратите внимание, что данные не перемешиваются случайным образом перед разделением. Это по двум причинам:
- Это гарантирует, что разделение данных на окна последовательных выборок по-прежнему возможно.
- Это гарантирует, что результаты проверки/тестирования будут более реалистичными, поскольку они оцениваются на основе данных, собранных после обучения модели.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
Нормализация данных
Перед обучением нейронной сети важно масштабировать функции. Нормализация — это распространенный способ масштабирования: вычесть среднее значение и разделить на стандартное отклонение каждого признака.
Среднее значение и стандартное отклонение следует вычислять только с использованием обучающих данных, чтобы модели не имели доступа к значениям в проверочных и тестовых наборах.
Также можно утверждать, что модель не должна иметь доступа к будущим значениям в тренировочном наборе во время обучения и что эта нормализация должна выполняться с использованием скользящих средних. Это не основное внимание в этом руководстве, а наборы проверки и тестирования гарантируют, что вы получите (в некоторой степени) честные метрики. Итак, в целях простоты в этом руководстве используется простое среднее значение.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
Теперь взгляните на распределение функций. У некоторых функций действительно есть длинные хвосты, но нет явных ошибок, таких как значение скорости ветра -9999 .
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

Окно данных
Модели в этом руководстве будут делать набор прогнозов на основе окна последовательных выборок из данных.
Основные особенности окон ввода:
- Ширина (количество временных шагов) окон ввода и метки.
- Смещение времени между ними.
- Какие функции используются в качестве входных данных, меток или того и другого.
В этом руководстве создаются различные модели (включая линейные модели, модели DNN, CNN и RNN) и используются они для обеих целей:
- Прогнозы с одним выходом и несколькими выходами .
- Прогнозы с одним и несколькими временными шагами .
В этом разделе основное внимание уделяется реализации окна данных, чтобы его можно было повторно использовать для всех этих моделей.
В зависимости от задачи и типа модели может потребоваться создание различных окон данных. Вот некоторые примеры:
Например, чтобы сделать один прогноз на 24 часа вперед, учитывая 24-часовую историю, вы можете определить окно следующим образом:
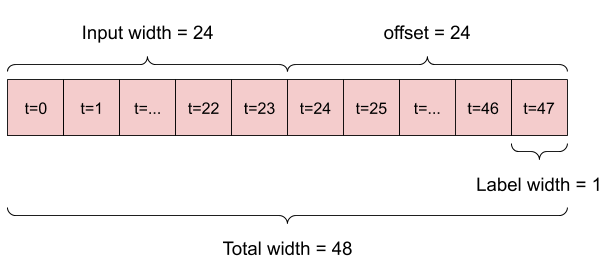
Модель, которая делает прогноз на один час вперед, учитывая шесть часов истории, нуждалась бы в таком окне:

В оставшейся части этого раздела определяется класс WindowGenerator . Этот класс может:
- Обрабатывайте индексы и смещения, как показано на диаграммах выше.
- Разделить окна функций на пары
(features, labels). - Постройте содержимое получившихся окон.
- Эффективно генерируйте пакеты этих окон из обучающих, оценочных и тестовых данных, используя
tf.data.Datasets.
1. Индексы и смещения
Начните с создания класса WindowGenerator . Метод __init__ включает всю необходимую логику для индексов ввода и меток.
Он также принимает обучающие, оценочные и тестовые кадры данных в качестве входных данных. Позже они будут преобразованы в tf.data.Dataset окон.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
Вот код для создания двух окон, показанных на диаграммах в начале этого раздела:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. Сплит
Учитывая список последовательных входных данных, метод split_window преобразует их в окно входных данных и окно меток.
Пример w2 , который вы определили ранее, будет разбит следующим образом:
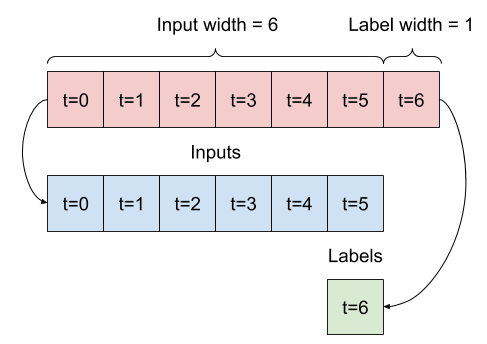
На этой диаграмме не показана ось features данных, но эта функция split_window также обрабатывает label_columns , поэтому ее можно использовать как для примеров с одним выходом, так и для примеров с несколькими выходами.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
Попробуйте:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
Как правило, данные в TensorFlow упаковываются в массивы, где самый внешний индекс находится среди примеров (размер «пакета»). Средние индексы - это измерение (я) «время» или «пространство» (ширина, высота). Самые внутренние индексы — это признаки.
В приведенном выше коде используется пакет из трех окон с 7 временными шагами с 19 функциями на каждом временном шаге. Он разбивает их на набор входных данных с 6 шагами по 19 функций и метку с 1 шагом по 1 функции. Метка имеет только одну функцию, потому что WindowGenerator был инициализирован с помощью label_columns=['T (degC)'] . Первоначально в этом учебном пособии будут построены модели, которые предсказывают одиночные выходные метки.
3. Сюжет
Вот метод построения графика, который позволяет легко визуализировать разделенное окно:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
Этот график выравнивает входные данные, метки и (более поздние) прогнозы на основе времени, к которому относится элемент:
w2.plot()
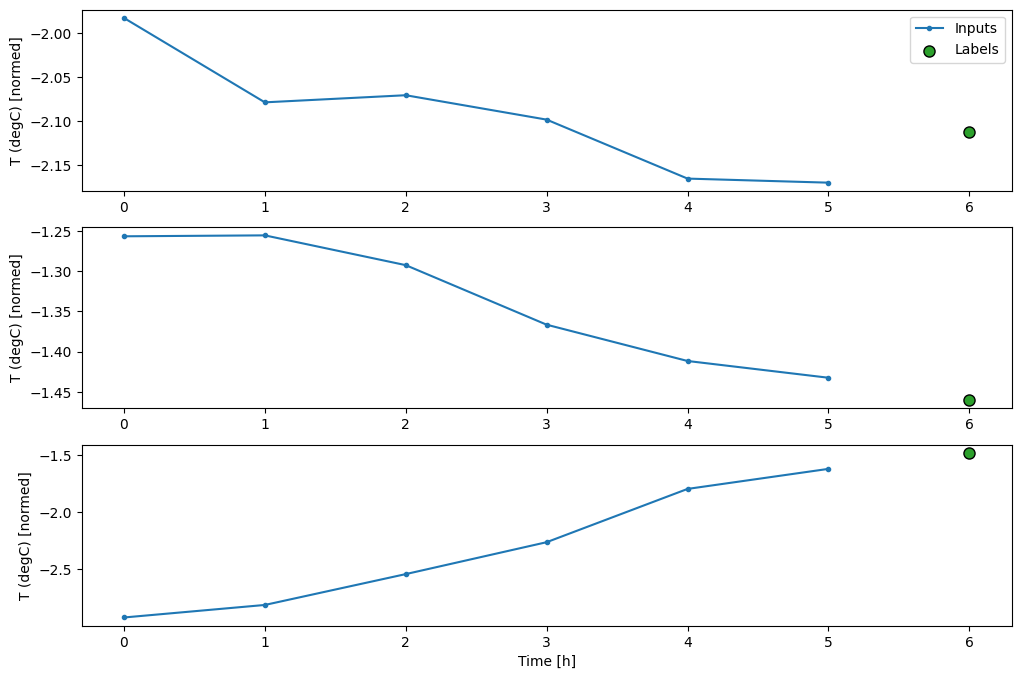
Вы можете построить другие столбцы, но пример конфигурации окна w2 имеет метки только для столбца T (degC) .
w2.plot(plot_col='p (mbar)')
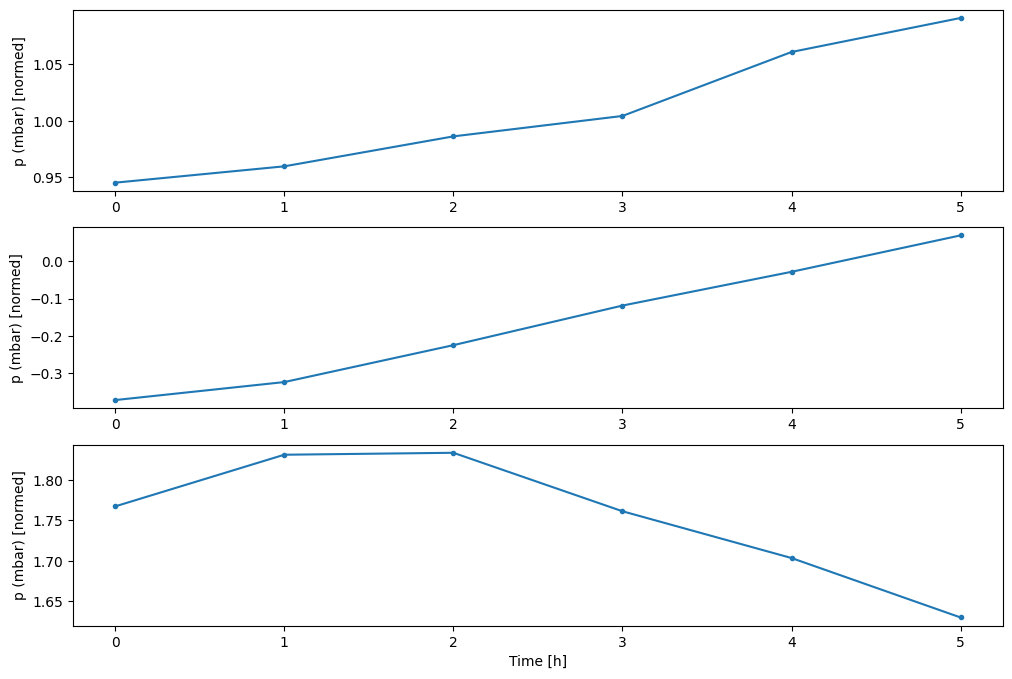
4. Создайте tf.data.Dataset s
Наконец, этот метод make_dataset возьмет временной ряд DataFrame и преобразует его в tf.data.Dataset из пар (input_window, label_window) с помощью функции tf.keras.utils.timeseries_dataset_from_array :
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
Объект WindowGenerator содержит обучающие, проверочные и тестовые данные.
Добавьте свойства для доступа к ним как tf.data.Dataset с помощью метода make_dataset , который вы определили ранее. Кроме того, добавьте стандартный пакет примеров для быстрого доступа и построения графиков:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
Теперь объект WindowGenerator предоставляет вам доступ к объектам tf.data.Dataset , поэтому вы можете легко перебирать данные.
Свойство Dataset.element_spec сообщает вам структуру, типы данных и формы элементов набора данных.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
Итерация по Dataset дает конкретные партии:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
Одноступенчатые модели
Самая простая модель, которую вы можете построить на такого рода данных, — это модель, которая предсказывает значение одной функции — 1 временной шаг (один час) в будущее, основываясь только на текущих условиях.
Итак, начните с построения моделей для прогнозирования значения T (degC) на один час вперед.
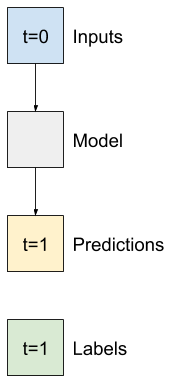
Настройте объект WindowGenerator для создания этих одношаговых пар (input, label) :
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
Объект window создает tf.data.Dataset из обучающих, проверочных и тестовых наборов, что позволяет легко перебирать пакеты данных.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
Базовый уровень
Перед созданием обучаемой модели было бы неплохо иметь базовый уровень производительности в качестве точки для сравнения с более поздними более сложными моделями.
Эта первая задача состоит в том, чтобы предсказать температуру на один час вперед, учитывая текущее значение всех признаков. Текущие значения включают текущую температуру.
Итак, начнем с модели, которая просто возвращает текущую температуру в качестве прогноза, прогнозируя «без изменений». Это разумная базовая линия, поскольку температура изменяется медленно. Конечно, эта базовая линия будет работать хуже, если вы сделаете прогноз в будущем.
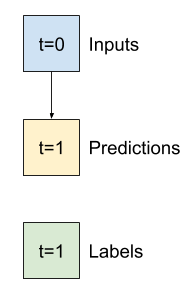
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
Создайте экземпляр и оцените эту модель:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
Это напечатало некоторые показатели производительности, но они не дают вам представления о том, насколько хорошо работает модель.
В WindowGenerator есть метод plot, но графики будут не очень интересными только с одним образцом.
Итак, создайте более широкий WindowGenerator , который генерирует окна 24 часа последовательных входных данных и меток за раз. Новая переменная wide_window не меняет способ работы модели. Модель по-прежнему делает прогнозы на один час вперед на основе одного входного временного шага. Здесь time ось действует как batch ось: каждый прогноз делается независимо, без взаимодействия между временными шагами:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
Это расширенное окно можно передать непосредственно в ту же baseline модель без каких-либо изменений кода. Это возможно, потому что входы и метки имеют одинаковое количество временных шагов, а базовая линия просто перенаправляет вход на выход:
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
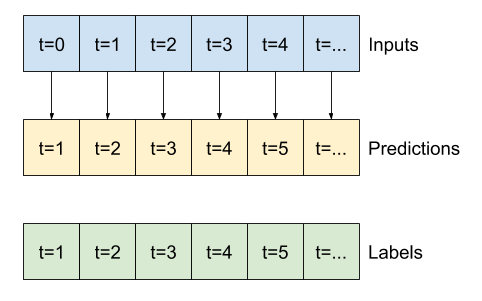
Построив прогнозы базовой модели, обратите внимание, что это просто метки, сдвинутые вправо на один час:
wide_window.plot(baseline)
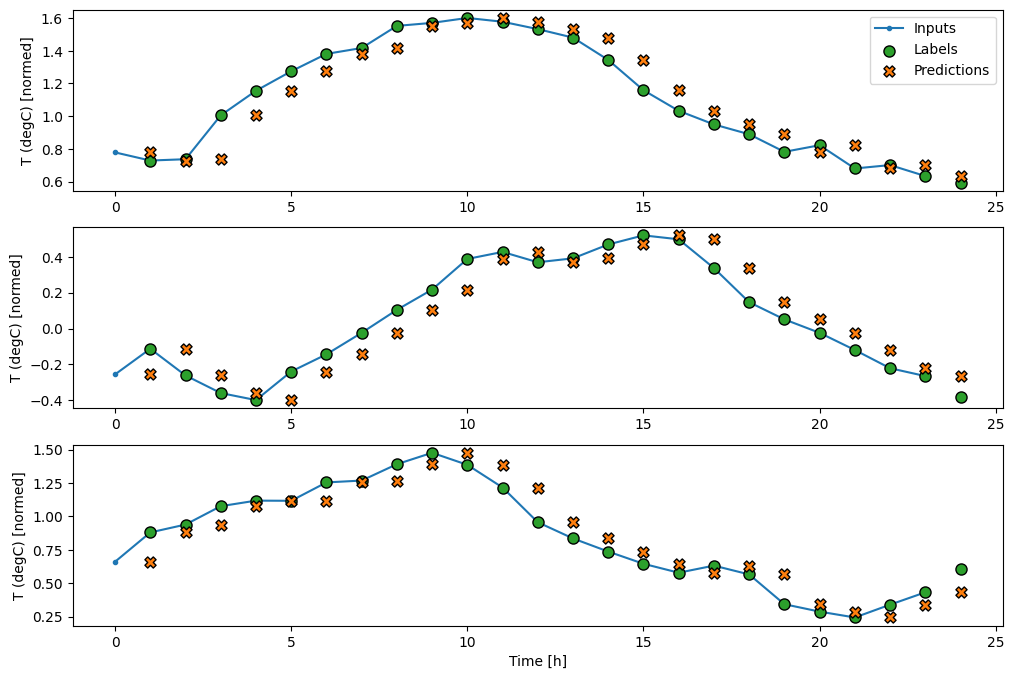
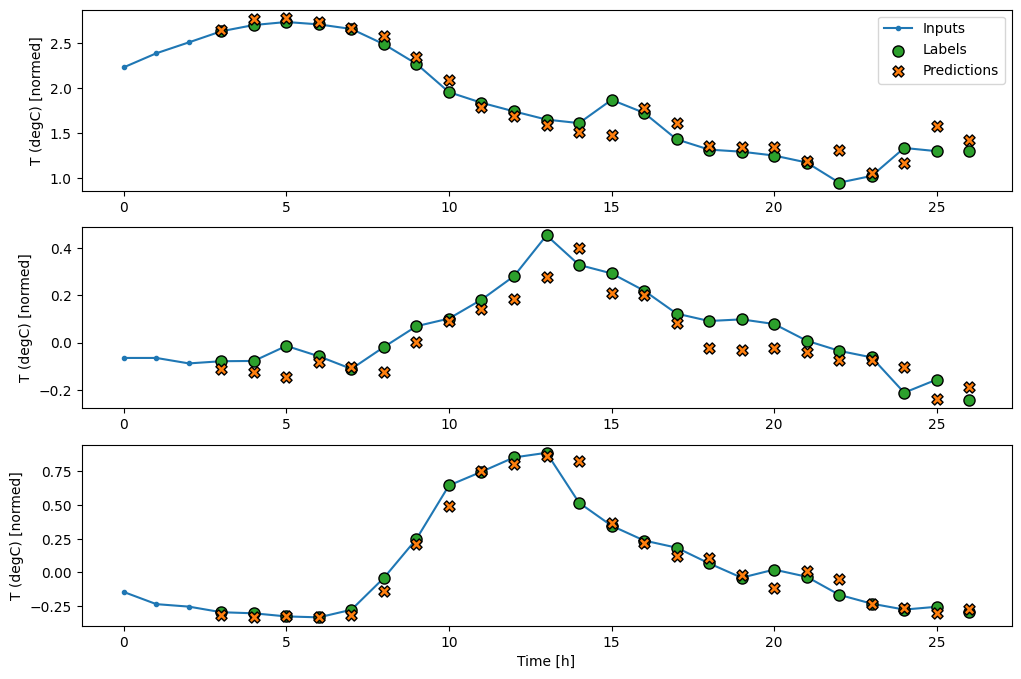
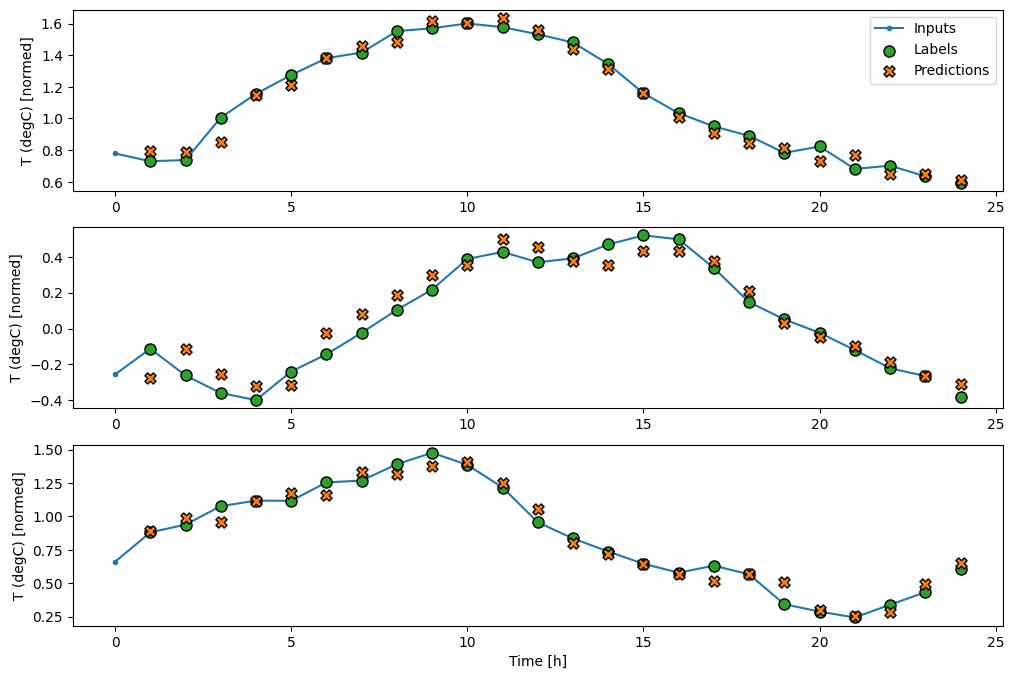
На приведенных выше графиках трех примеров одноэтапная модель работает в течение 24 часов. Это заслуживает некоторого пояснения:
- Синяя линия
Inputsпоказывает входную температуру на каждом временном шаге. Модель получает все функции, этот график показывает только температуру. - Зеленые точки
Labelsпоказывают целевое значение прогноза. Эти точки отображаются во время прогнозирования, а не во время ввода. Поэтому диапазон меток смещен на 1 шаг относительно входов. - Оранжевые кресты
Predictions— это прогнозы модели для каждого выходного временного шага. Если бы модель предсказывала идеально, прогнозы попадали бы прямо вLabels.
Линейная модель
Самая простая обучаемая модель, которую вы можете применить к этой задаче, — это вставить линейное преобразование между входом и выходом. В этом случае результат временного шага зависит только от этого шага:

Слой tf.keras.layers.Dense без набора activation является линейной моделью. Слой преобразует только последнюю ось данных из (batch, time, inputs) в (batch, time, units) ; он применяется независимо к каждому элементу по осям batch и time .
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
В этом руководстве обучается множество моделей, поэтому упакуйте процедуру обучения в функцию:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
Обучите модель и оцените ее производительность:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
Как и baseline модель, линейную модель можно вызывать для пакетов широких окон. При таком использовании модель делает набор независимых прогнозов на последовательных временных шагах. Ось time действует как другая ось batch . Между прогнозами на каждом временном шаге нет взаимодействий.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
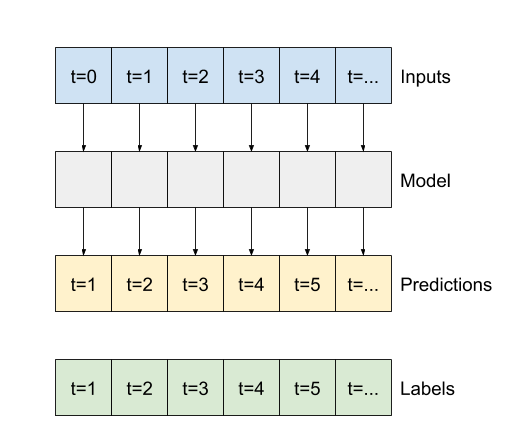
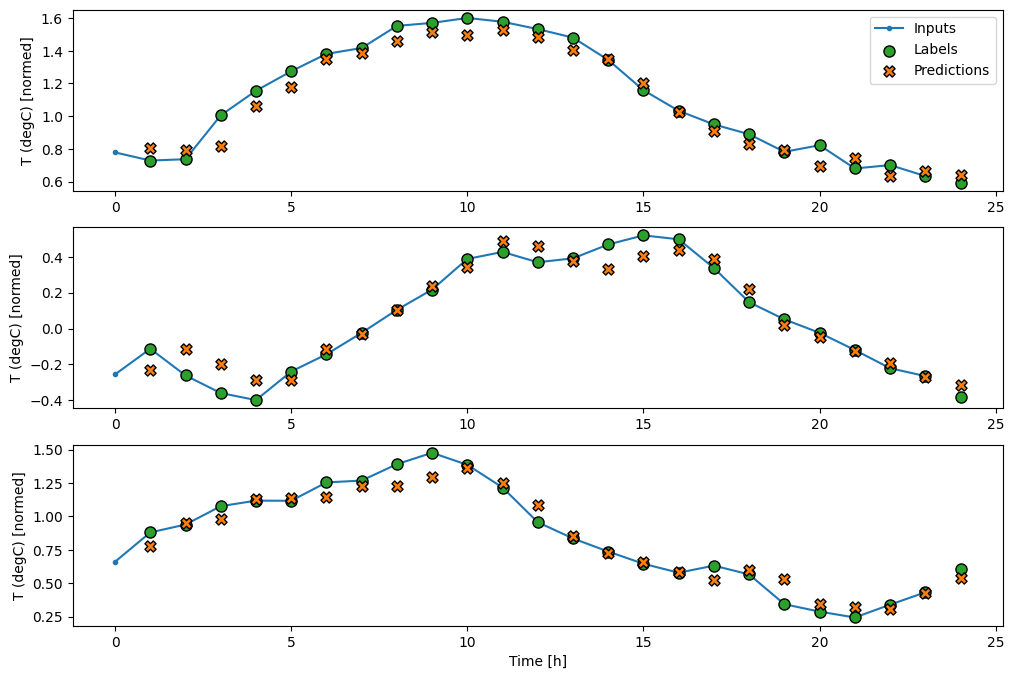
Вот график его примерных прогнозов для wide_window , обратите внимание, что во многих случаях прогноз явно лучше, чем просто возврат входной температуры, но в некоторых случаях он хуже:
wide_window.plot(linear)
Одним из преимуществ линейных моделей является то, что их относительно просто интерпретировать. Вы можете вытащить веса слоя и визуализировать вес, назначенный каждому входу:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
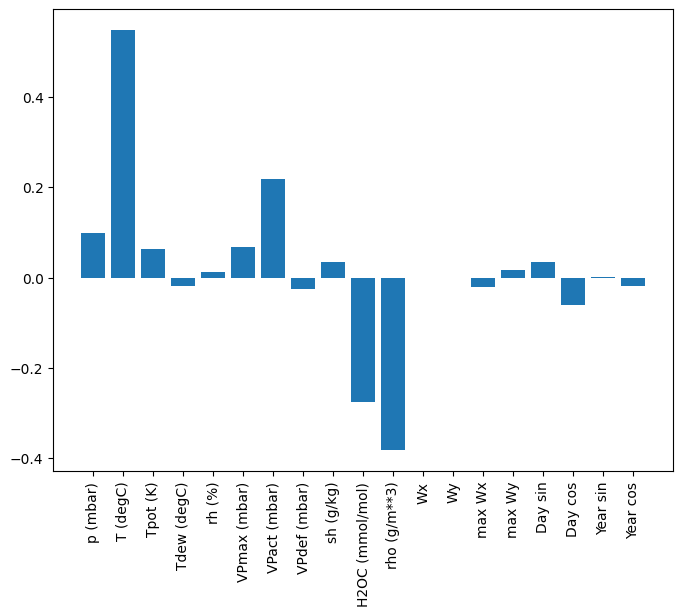
Иногда модель даже не придает значения входным данным T (degC) . Это один из рисков случайной инициализации.
Плотный
Прежде чем применять модели, которые фактически работают с несколькими временными шагами, стоит проверить производительность более глубоких и мощных моделей с одним входным шагом.
Вот модель, похожая на linear модель, за исключением того, что между входом и выходом укладывается несколько Dense слоев:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
Многоступенчатый плотный
Одношаговая модель не имеет контекста для текущих значений входных данных. Он не может видеть, как входные объекты меняются с течением времени. Чтобы решить эту проблему, модели требуется доступ к нескольким временным шагам при прогнозировании:
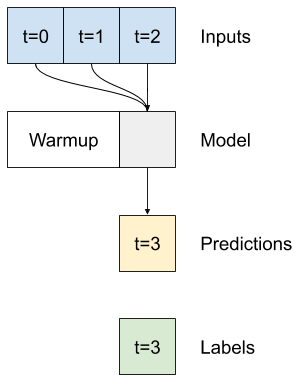
baseline , linear и dense модели обрабатывали каждый временной шаг независимо. Здесь модель будет принимать несколько временных шагов в качестве входных данных для получения одного вывода.
Создайте WindowGenerator , который будет создавать пакеты трехчасовых входных данных и одночасовых меток:
Обратите внимание, что параметр shift Window относится к концу двух окон.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
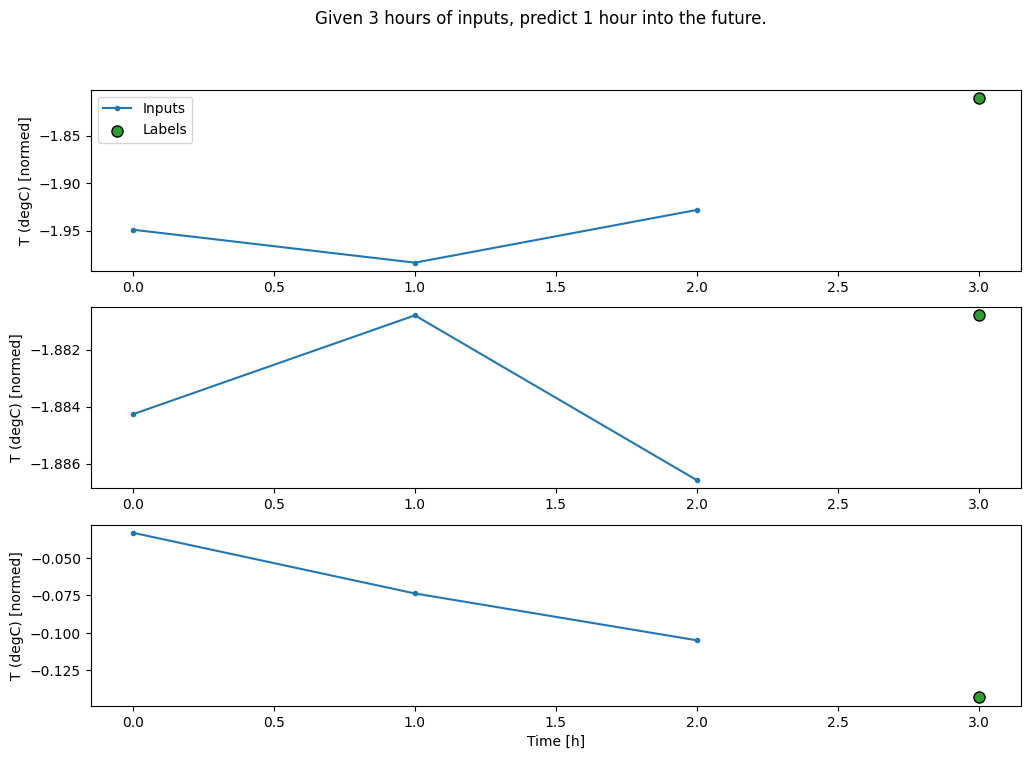
Вы можете обучить dense модель в окне с несколькими входными шагами, добавив tf.keras.layers.Flatten в качестве первого слоя модели:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
conv_window.plot(multi_step_dense)
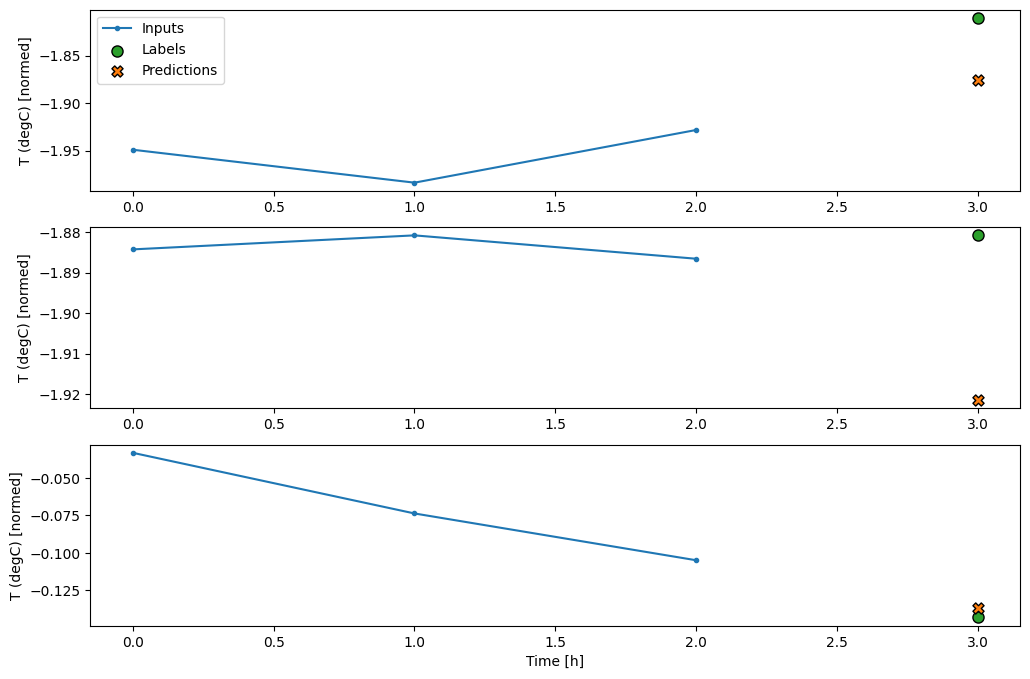
Основным недостатком этого подхода является то, что результирующая модель может выполняться только на входных окнах именно такой формы.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
Сверточные модели в следующем разделе решают эту проблему.
Сверточная нейронная сеть
Слой свертки ( tf.keras.layers.Conv1D ) также использует несколько временных шагов в качестве входных данных для каждого прогноза.
Ниже представлена та же модель, что и в multi_step_dense , переписанная с помощью свертки.
Обратите внимание на изменения:
-
tf.keras.layers.Flattenи первыйtf.keras.layers.Denseзаменяютсяtf.keras.layers.Conv1D. -
tf.keras.layers.Reshapeбольше не нужен, так как свертка сохраняет ось времени в своих выходных данных.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
Запустите его на примере пакета, чтобы убедиться, что модель выдает выходные данные с ожидаемой формой:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
Обучите и оцените его в conv_window и он должен дать производительность, аналогичную модели multi_step_dense .
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
Разница между этой conv_model и моделью multi_step_dense заключается в том, что conv_model можно запускать на входах любой длины. Сверточный слой применяется к скользящему окну входных данных:
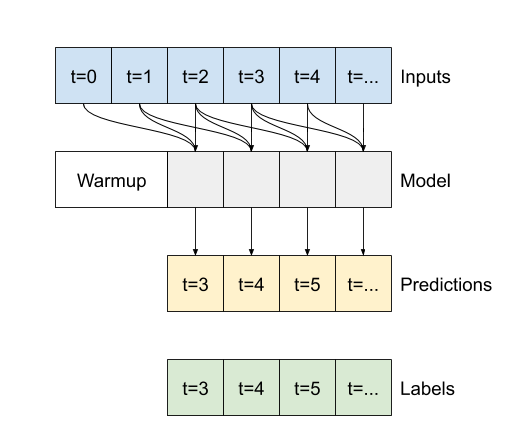
Если вы запустите его на более широком вводе, он выдаст более широкий вывод:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
Обратите внимание, что вывод короче ввода. Чтобы обучение или построение графика работали, вам нужно, чтобы метки и прогноз имели одинаковую длину. Поэтому создайте WindowGenerator для создания широких окон с несколькими дополнительными временными шагами ввода, чтобы длина метки и предсказания совпадала:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
Теперь вы можете построить прогнозы модели в более широком окне. Обратите внимание на 3 шага входного времени перед первым прогнозом. Каждый прогноз здесь основан на 3 предыдущих временных шагах:
wide_conv_window.plot(conv_model)
Рекуррентная нейронная сеть
Рекуррентная нейронная сеть (RNN) — это тип нейронной сети, хорошо подходящий для данных временных рядов. RNN обрабатывают временной ряд шаг за шагом, сохраняя внутреннее состояние от шага к шагу.
Вы можете узнать больше о создании текста с помощью учебника по RNN и о рекуррентных нейронных сетях (RNN) с руководством по Keras .
В этом руководстве вы будете использовать слой RNN под названием Long Short-Term Memory ( tf.keras.layers.LSTM ).
Важным аргументом конструктора для всех слоев Keras RNN, таких как tf.keras.layers.LSTM , является аргумент return_sequences . Этот параметр может настроить слой одним из двух способов:
- Если
Falseпо умолчанию, слой возвращает только выходные данные последнего временного шага, давая модели время, чтобы прогреть свое внутреннее состояние, прежде чем делать один прогноз:
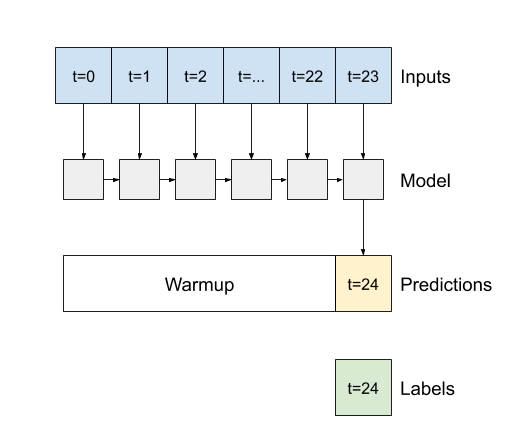
- Если
True, слой возвращает результат для каждого входа. Это полезно для:- Укладка слоев RNN.
- Обучение модели на нескольких временных шагах одновременно.
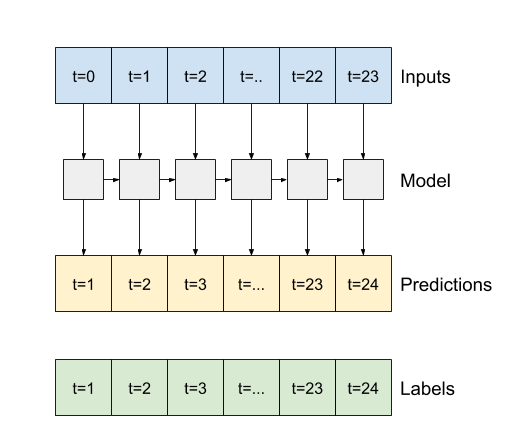
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
С return_sequences=True модель можно обучать на данных за 24 часа за раз.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
wide_window.plot(lstm_model)
Представление
С этим набором данных обычно каждая из моделей работает немного лучше, чем предыдущая:
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()
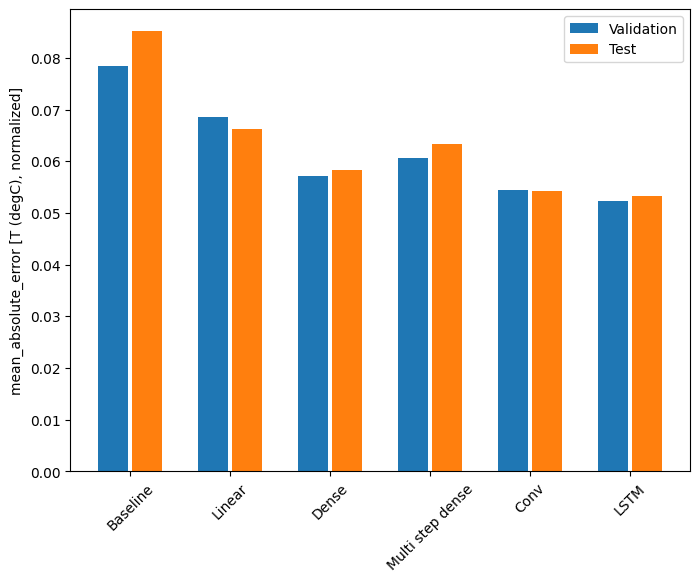
for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
Модели с несколькими выходами
До сих пор все модели предсказывали одну выходную характеристику T (degC) для одного временного шага.
Все эти модели можно преобразовать для прогнозирования нескольких функций, просто изменив количество единиц в выходном слое и настроив окна обучения, чтобы включить все функции в labels ( example_labels ):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
Обратите внимание, что ось features меток теперь имеет ту же глубину, что и входные данные, а не 1 .
Базовый уровень
Здесь можно использовать ту же базовую модель ( Baseline ), но на этот раз с повторением всех функций вместо выбора конкретного label_index :
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
Плотный
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
РНН
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
Дополнительно: Остаточные соединения
Baseline модель, использованная ранее, использовала тот факт, что последовательность не сильно меняется от одного временного шага к другому. Каждая модель, обученная в этом руководстве до сих пор, была случайным образом инициализирована, а затем должна была узнать, что результат представляет собой небольшое изменение по сравнению с предыдущим временным шагом.
Хотя вы можете обойти эту проблему с помощью тщательной инициализации, проще встроить ее в структуру модели.
В анализе временных рядов обычно строят модели, которые вместо предсказания следующего значения предсказывают, как значение изменится на следующем временном шаге. Точно так же остаточные сети — или ResNets — в глубоком обучении относятся к архитектурам, в которых каждый уровень добавляется к накапливающемуся результату модели.
Вот как вы пользуетесь знанием того, что изменение должно быть небольшим.
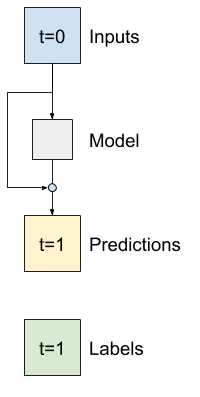
По сути, это инициализирует модель в соответствии с Baseline . Для этой задачи это помогает моделям быстрее сходиться с немного лучшей производительностью.
Этот подход можно использовать в сочетании с любой моделью, обсуждаемой в этом руководстве.
Здесь он применяется к модели LSTM, обратите внимание на использование tf.initializers.zeros , чтобы гарантировать, что начальные прогнозируемые изменения будут небольшими и не пересилят остаточное соединение. Здесь нет проблем с нарушением симметрии для градиентов, поскольку zeros используются только на последнем слое.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
Представление
Вот общая производительность для этих моделей с несколькими выходами.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
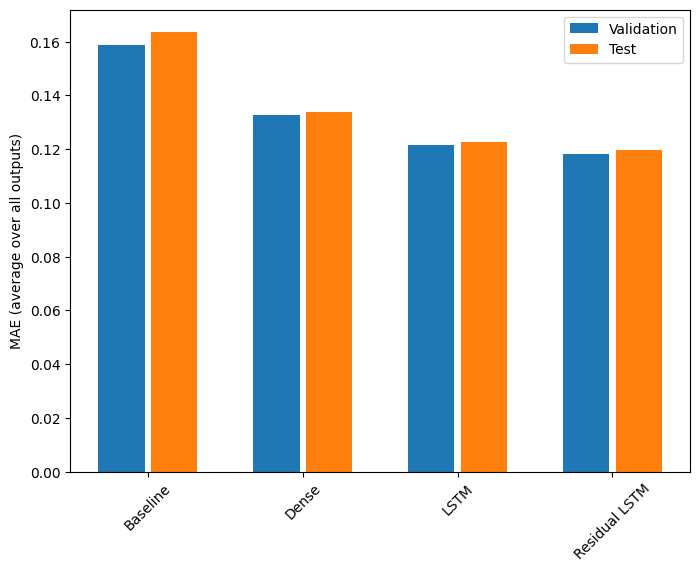
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
Приведенные выше характеристики усреднены по всем выходным данным модели.
Многошаговые модели
Как модели с одним выходом, так и модели с несколькими выходами в предыдущих разделах делали прогнозы с одним временным шагом , на один час вперед.
В этом разделе рассматривается, как расширить эти модели, чтобы делать прогнозы с несколькими временными шагами .
В многоэтапном прогнозировании модель должна научиться прогнозировать диапазон будущих значений. Таким образом, в отличие от одноступенчатой модели, в которой предсказывается только одна точка будущего, многоступенчатая модель предсказывает последовательность будущих значений.
Есть два грубых подхода к этому:
- Прогнозы одиночного выстрела, когда весь временной ряд прогнозируется сразу.
- Прогнозы авторегрессии, при которых модель делает только одношаговые прогнозы, а ее выходные данные возвращаются в качестве входных данных.
В этом разделе все модели будут предсказывать все функции на всех выходных временных шагах .
Для многоступенчатой модели обучающие данные снова состоят из ежечасных выборок. Однако здесь модели научатся предсказывать будущее на 24 часа, учитывая 24 часа прошлого.
Вот объект Window , который генерирует эти срезы из набора данных:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
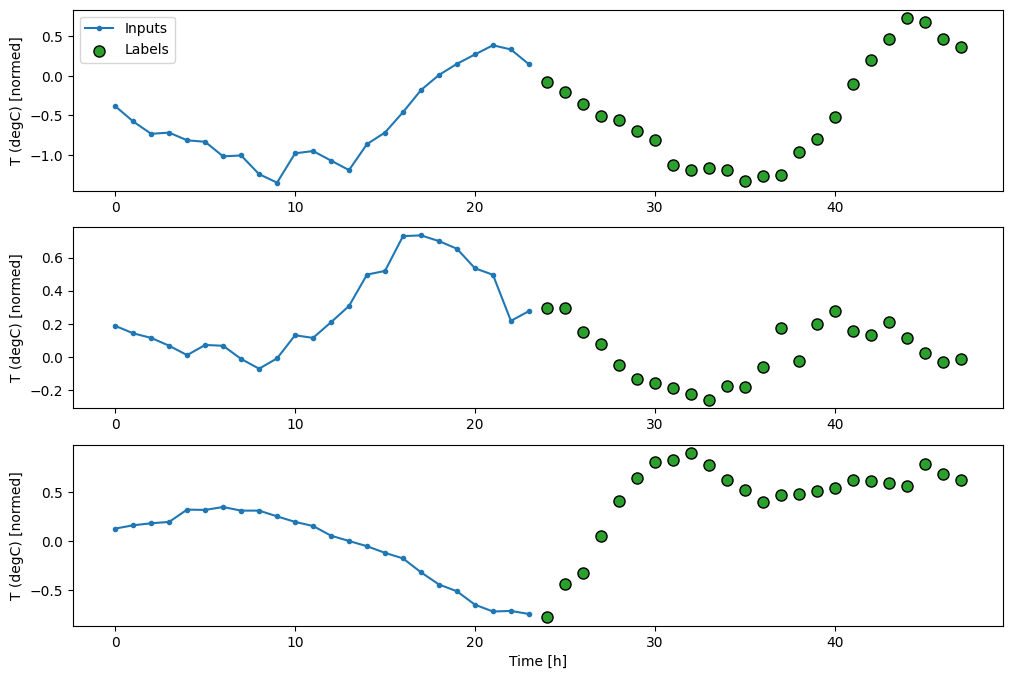
Базовые показатели
Простая базовая линия для этой задачи — повторить последний временной шаг ввода для необходимого количества выходных временных шагов:
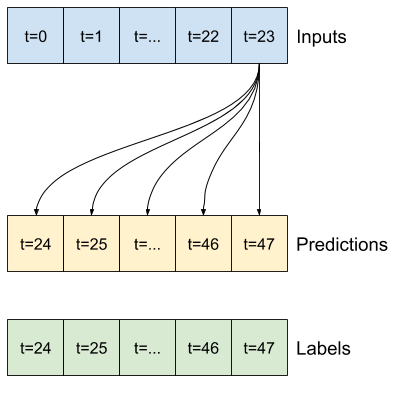
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
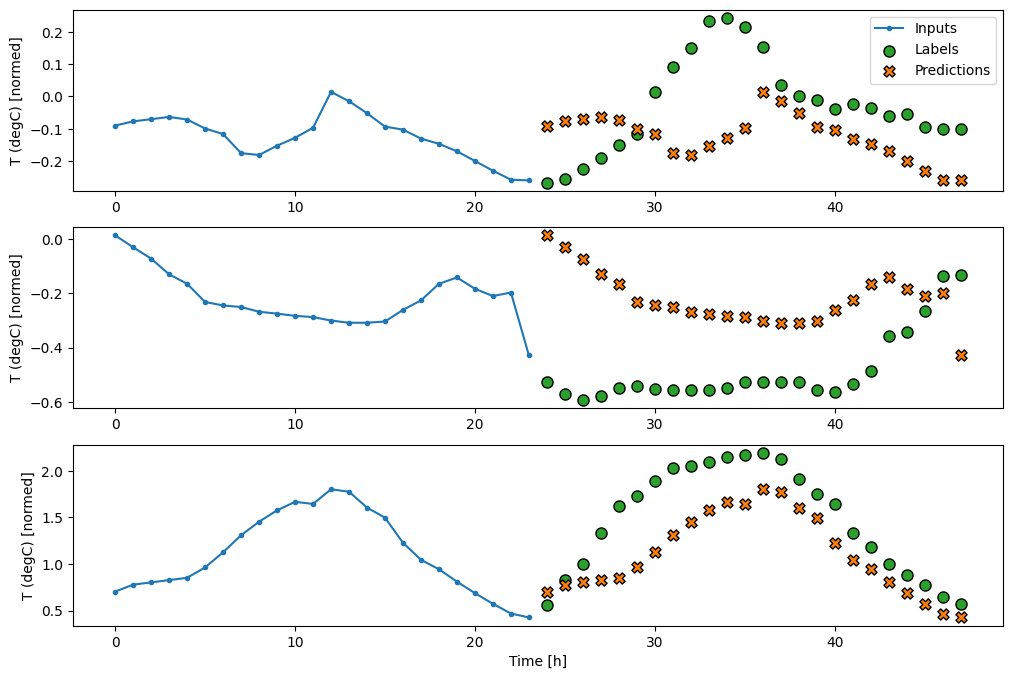
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007
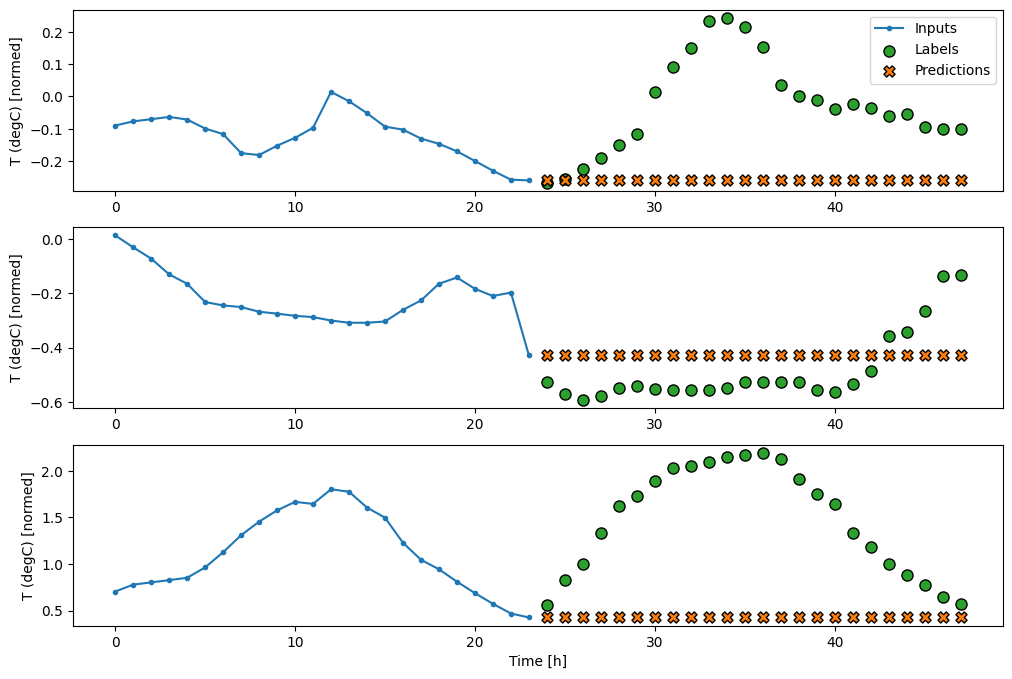
Поскольку эта задача состоит в том, чтобы предсказать 24 часа в будущем, учитывая 24 часа в прошлом, другой простой подход состоит в том, чтобы повторить предыдущий день, предполагая, что завтра будет похоже:
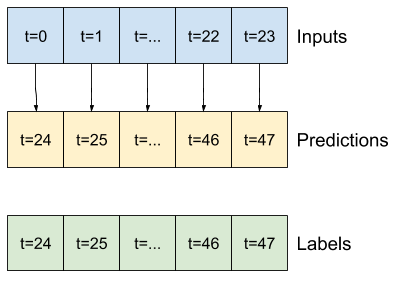
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
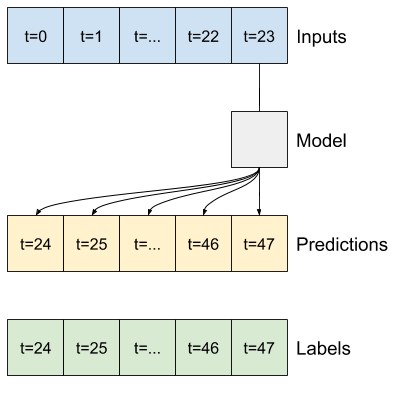
Однозарядные модели
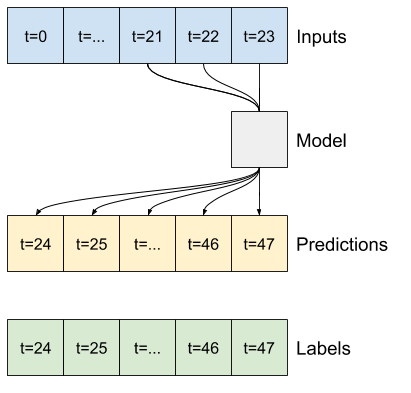
Одним из высокоуровневых подходов к этой проблеме является использование «однократной» модели, в которой модель делает прогноз всей последовательности за один шаг.
Это может быть эффективно реализовано как tf.keras.layers.Dense с выходными единицами OUT_STEPS*features . Модель просто должна преобразовать этот вывод в требуемый (OUTPUT_STEPS, features) .
Линейный
Простая линейная модель, основанная на последнем входном временном шаге, работает лучше любой базовой линии, но у нее недостаточно мощности. Модель должна прогнозировать временные шаги OUTPUT_STEPS на основе одного входного временного шага с линейной проекцией. Он может зафиксировать только низкоразмерный фрагмент поведения, вероятно, основанный в основном на времени суток и времени года.
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053
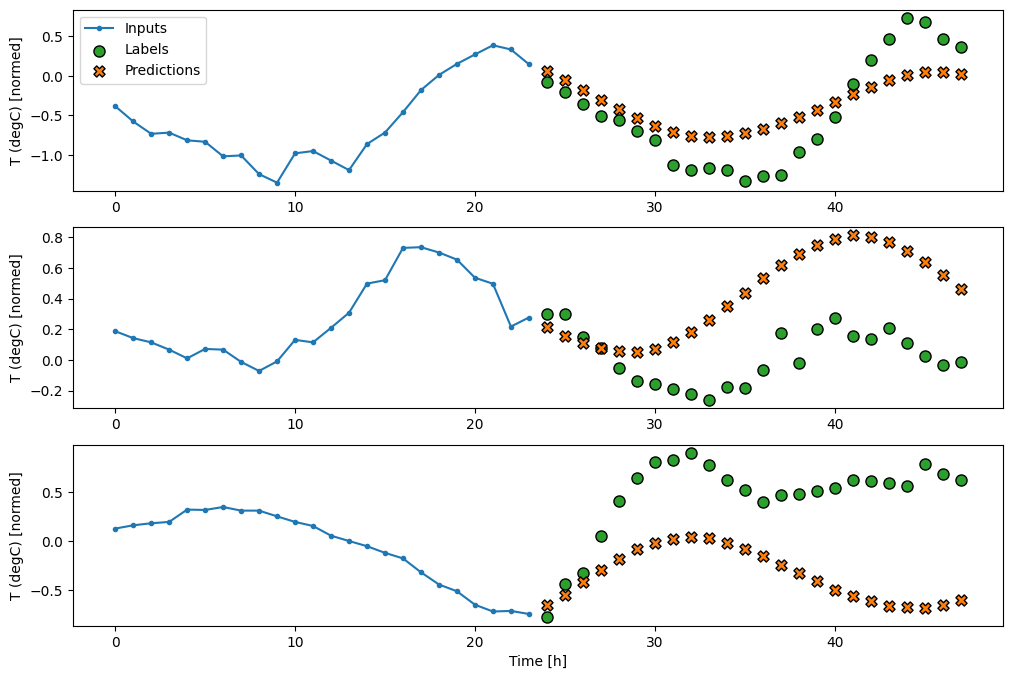
Плотный
Добавление tf.keras.layers.Dense между входом и выходом делает линейную модель более мощной, но по-прежнему основано только на одном временном шаге ввода.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
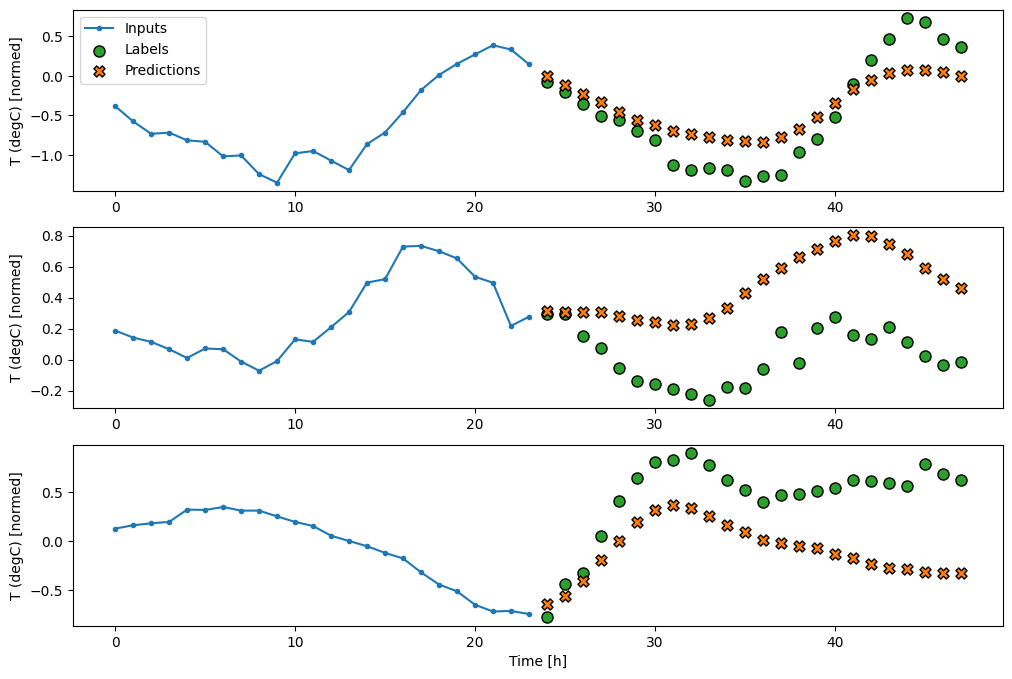
Си-Эн-Эн
Сверточная модель делает прогнозы на основе истории фиксированной ширины, что может привести к более высокой производительности, чем плотная модель, поскольку она может видеть, как все меняется с течением времени:
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
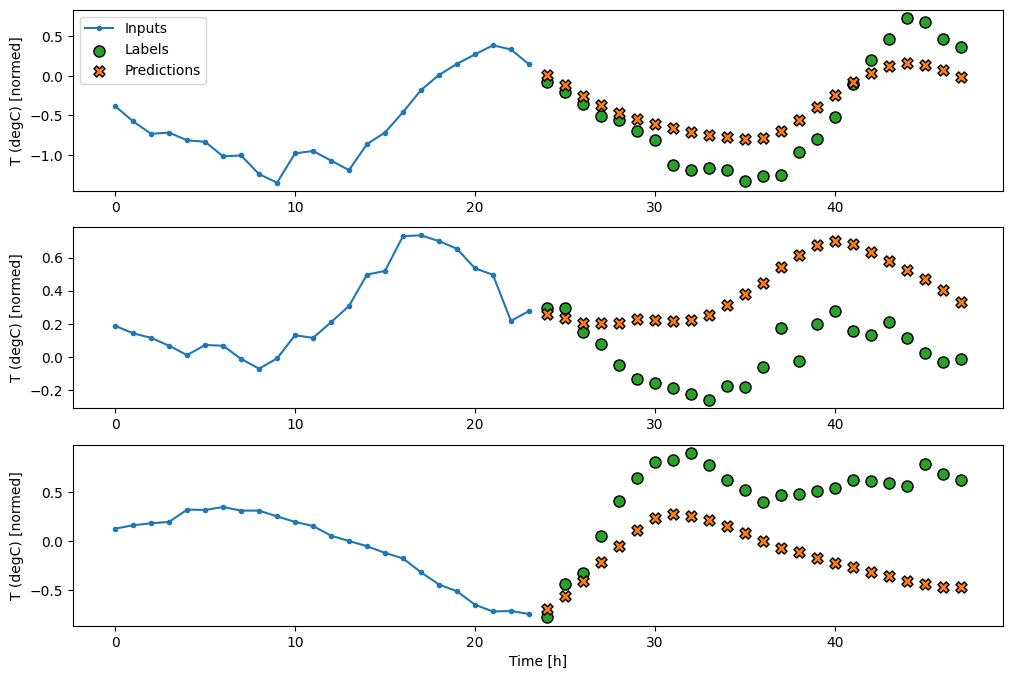
РНН
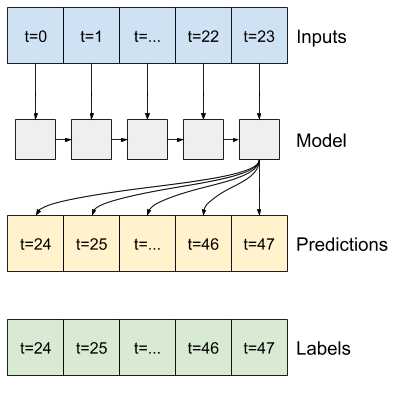
Рекуррентная модель может научиться использовать длинную историю входных данных, если она имеет отношение к прогнозам, которые делает модель. Здесь модель будет накапливать внутреннее состояние за 24 часа, прежде чем сделать один прогноз на следующие 24 часа.
В этом однократном формате LSTM нужно выводить только на последнем временном шаге, поэтому установите return_sequences=False в tf.keras.layers.LSTM .
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
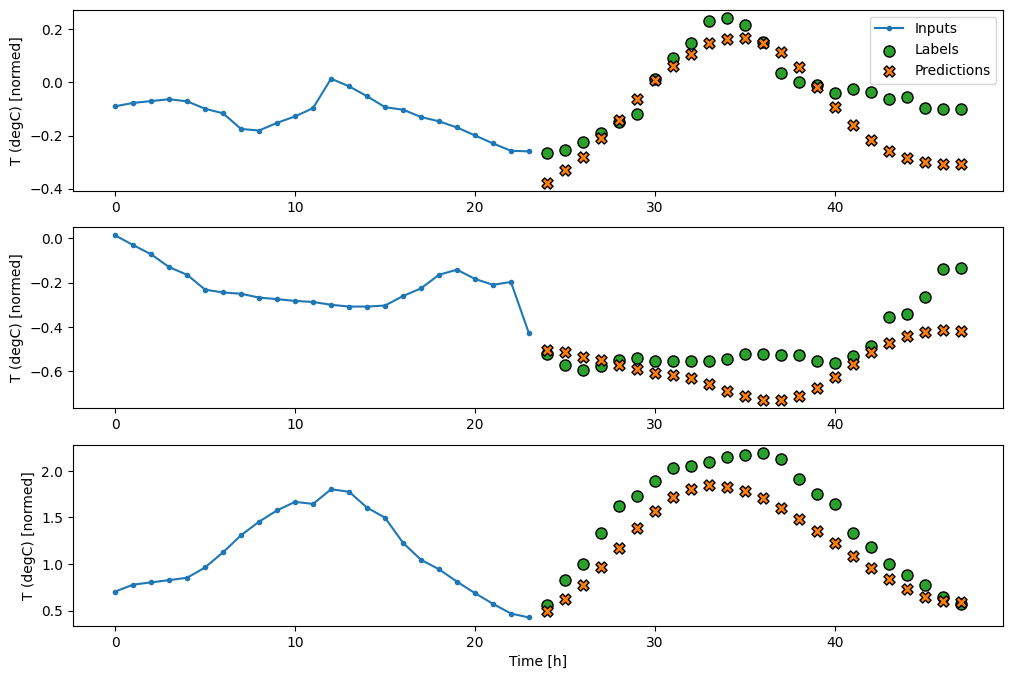
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
Дополнительно: авторегрессионная модель
Все вышеперечисленные модели предсказывают всю выходную последовательность за один шаг.
В некоторых случаях для модели может быть полезно разложить этот прогноз на отдельные временные шаги. Затем выходные данные каждой модели могут быть возвращены в себя на каждом шаге, и прогнозы могут быть сделаны в зависимости от предыдущего, как в классическом Генерация последовательностей с рекуррентными нейронными сетями .
Одним из явных преимуществ модели этого типа является то, что ее можно настроить для получения выходных данных различной длины.
Вы можете взять любую из одноэтапных моделей с несколькими выходами, обученных в первой половине этого руководства, и запустить авторегрессионный цикл обратной связи, но здесь вы сосредоточитесь на построении модели, специально обученной для этого.
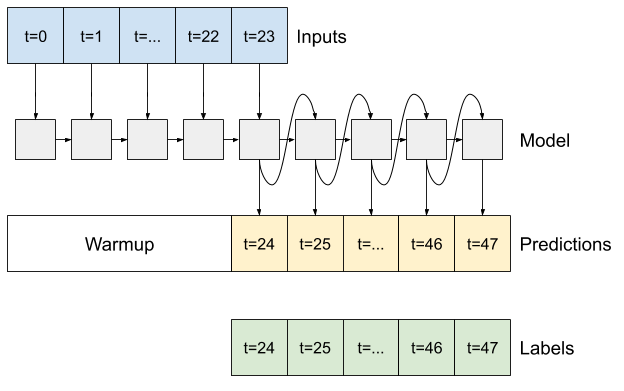
РНН
В этом руководстве строится только авторегрессионная модель RNN, но этот шаблон можно применить к любой модели, предназначенной для вывода одного временного шага.
Модель будет иметь ту же базовую форму, что и одноэтапные модели LSTM из более ранних версий: слой tf.keras.layers.LSTM , за которым следует слой tf.keras.layers.Dense , который преобразует выходные данные слоя LSTM в прогнозы модели.
tf.keras.layers.LSTM — это tf.keras.layers.LSTMCell , обернутый в tf.keras.layers.RNN более высокого уровня, который управляет для вас результатами состояния и последовательности (ознакомьтесь с рекуррентными нейронными сетями (RNN) с Keras). руководство для получения подробной информации).
В этом случае модель должна вручную управлять входными данными для каждого шага, поэтому она использует tf.keras.layers.LSTMCell непосредственно для интерфейса нижнего уровня с одним временным шагом.
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
Первый метод, в котором нуждается эта модель, — это метод warmup для инициализации ее внутреннего состояния на основе входных данных. После обучения это состояние будет захватывать соответствующие части истории ввода. Это эквивалентно одноэтапной модели LSTM из более раннего:
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
Этот метод возвращает прогноз с одним временным шагом и внутреннее состояние LSTM :
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
С состоянием RNN и начальным прогнозом теперь вы можете продолжить итерацию модели, передавая прогнозы на каждом шагу назад в качестве входных данных.
Самый простой подход к сбору выходных прогнозов — использовать список Python и tf.stack после цикла.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
Протестируйте эту модель на входных данных примера:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
Теперь обучите модель:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
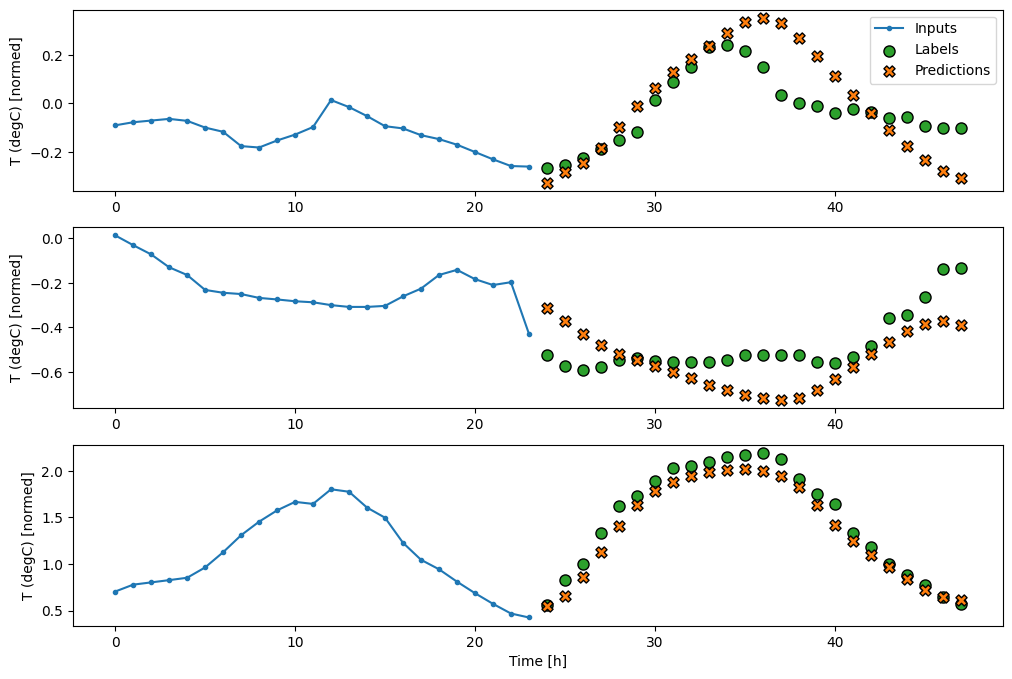
Представление
В этой проблеме явно наблюдается уменьшение отдачи в зависимости от сложности модели:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()
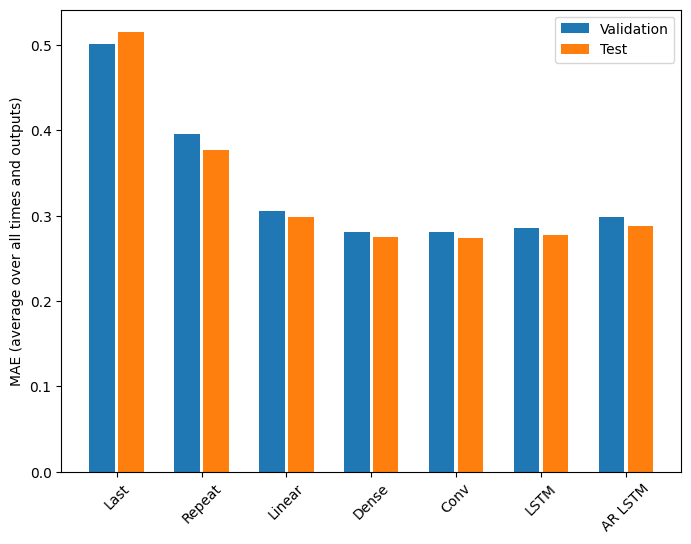
Метрики для моделей с несколькими выходами в первой половине этого руководства показывают среднюю производительность по всем выходным функциям. Эти характеристики аналогичны, но также усреднены по временным шагам вывода.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
Выигрыш, достигнутый при переходе от плотной модели к сверточной и рекуррентной моделям, составляет всего несколько процентов (если вообще есть), а авторегрессионная модель показала себя явно хуже. Таким образом, эти более сложные подходы могут быть бесполезными для решения этой проблемы, но невозможно было узнать, не попробовав, и эти модели могут быть полезны для решения вашей проблемы.
Следующие шаги
Это руководство было кратким введением в прогнозирование временных рядов с использованием TensorFlow.
Чтобы узнать больше, см.:
- Глава 15 практического машинного обучения с помощью Scikit-Learn, Keras и TensorFlow , 2-е издание.
- Глава 6 Глубокого обучения с помощью Python .
- Урок 8 введения Udacity в TensorFlow для глубокого обучения , включая тетради с упражнениями.
Кроме того, помните, что вы можете реализовать любую классическую модель временных рядов в TensorFlow — это руководство фокусируется только на встроенных функциях TensorFlow.
