 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Hướng dẫn này là phần giới thiệu về dự báo chuỗi thời gian bằng TensorFlow. Nó xây dựng một số kiểu mô hình khác nhau bao gồm Mạng thần kinh chuyển đổi và mạng tái tạo (CNN và RNN).
Điều này được bao gồm trong hai phần chính, với các phần phụ:
- Dự báo cho một bước thời gian duy nhất:
- Một tính năng duy nhất.
- Tất cả các tính năng.
- Dự báo nhiều bước:
- Một lần chụp: Đưa ra tất cả các dự đoán cùng một lúc.
- Tự động hồi quy: Đưa ra một dự đoán tại một thời điểm và đưa đầu ra trở lại mô hình.
Thành lập
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
Bộ dữ liệu thời tiết
Hướng dẫn này sử dụng tập dữ liệu chuỗi thời gian thời tiết được ghi lại bởi Viện Hóa sinh Sinh học Max Planck .
Bộ dữ liệu này chứa 14 đặc điểm khác nhau như nhiệt độ không khí, áp suất khí quyển và độ ẩm. Chúng được thu thập cứ 10 phút một lần, bắt đầu từ năm 2003. Để đạt hiệu quả cao, bạn sẽ chỉ sử dụng dữ liệu được thu thập từ năm 2009 đến năm 2016. Phần này của tập dữ liệu được François Chollet chuẩn bị cho cuốn sách Học sâu với Python .
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13574144/13568290 [==============================] - 1s 0us/step 13582336/13568290 [==============================] - 1s 0us/step
Hướng dẫn này sẽ chỉ giải quyết các dự đoán hàng giờ , vì vậy hãy bắt đầu bằng cách lấy mẫu con dữ liệu từ khoảng thời gian 10 phút đến khoảng thời gian một giờ:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
Hãy xem qua dữ liệu. Đây là một số hàng đầu tiên:
df.head()
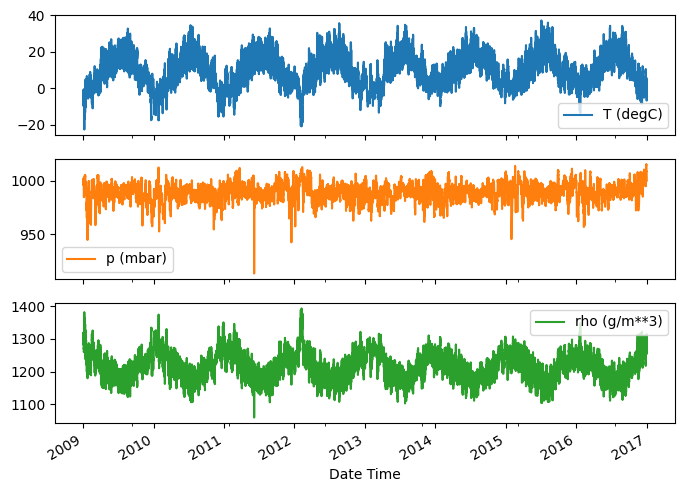
Dưới đây là sự phát triển của một số tính năng theo thời gian:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
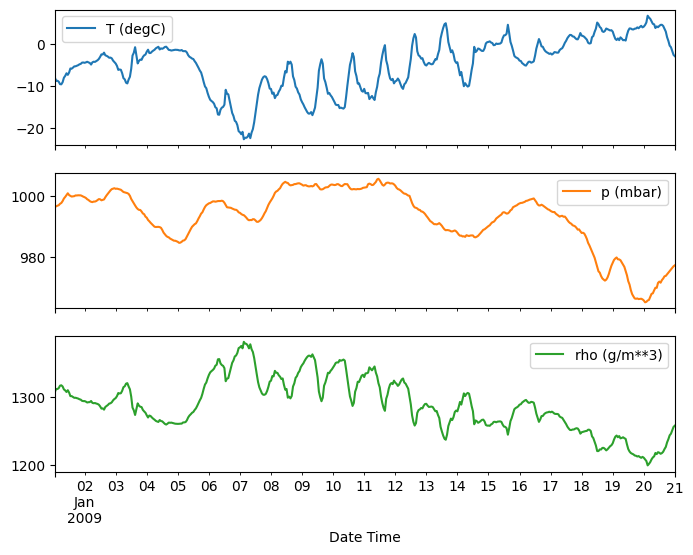
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
Kiểm tra và dọn dẹp
Tiếp theo, hãy xem thống kê của tập dữ liệu:
df.describe().transpose()
Vận tốc gió
Một điều cần nổi bật là giá trị nhỏ nhất của các cột vận tốc gió ( wv (m/s) min và giá trị lớn nhất ( max. wv (m/s) ). -9999 này có thể bị sai.
Có một cột hướng gió riêng biệt, vì vậy vận tốc phải lớn hơn 0 ( >=0 ). Thay thế nó bằng các số không:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
Kỹ thuật tính năng
Trước khi bắt đầu xây dựng mô hình, điều quan trọng là phải hiểu dữ liệu của bạn và đảm bảo rằng bạn đang chuyển dữ liệu được định dạng phù hợp cho mô hình.
Gió
Cột cuối cùng của dữ liệu, wd (deg) —giới thiệu hướng gió theo đơn vị độ. Các góc không tạo ra đầu vào mô hình tốt: 360 ° và 0 ° phải gần nhau và quấn quanh trơn tru. Phương hướng sẽ không thành vấn đề nếu gió không thổi.
Ngay bây giờ, việc phân phối dữ liệu gió trông giống như sau:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
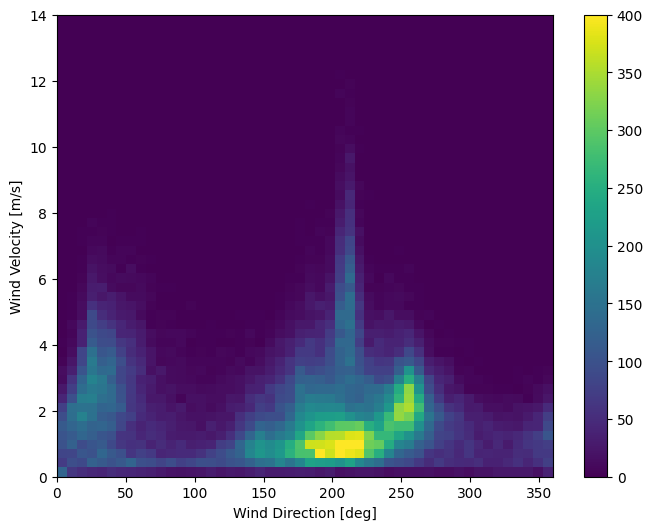
Nhưng điều này sẽ dễ dàng hơn cho mô hình giải thích nếu bạn chuyển đổi các cột hướng gió và vận tốc thành vectơ gió:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
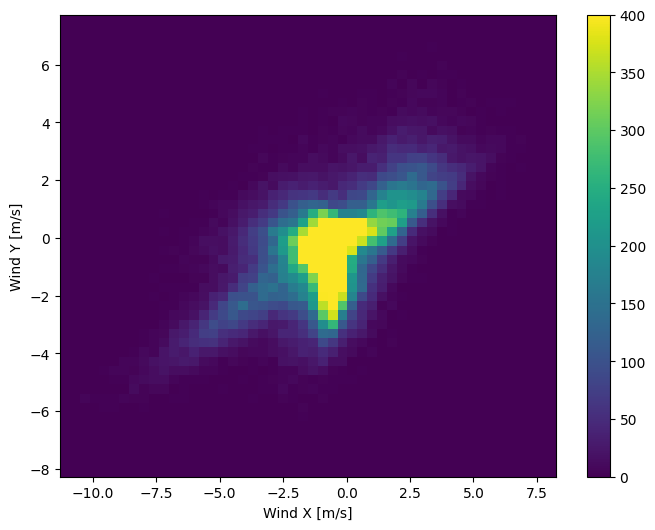
Sự phân bố của các vectơ gió đơn giản hơn nhiều để mô hình giải thích một cách chính xác:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
Thời gian
Tương tự, cột Date Time rất hữu ích, nhưng không phải ở dạng chuỗi này. Bắt đầu bằng cách chuyển đổi nó thành giây:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
Tương tự như hướng gió, thời gian tính bằng giây không phải là đầu vào mô hình hữu ích. Là dữ liệu thời tiết, nó có tính định kỳ hàng ngày và hàng năm rõ ràng. Có nhiều cách bạn có thể đối phó với tính chu kỳ.
Bạn có thể nhận được các tín hiệu có thể sử dụng bằng cách sử dụng các phép biến đổi sin và côsin để xóa các tín hiệu "Thời gian trong ngày" và "Thời gian trong năm":
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
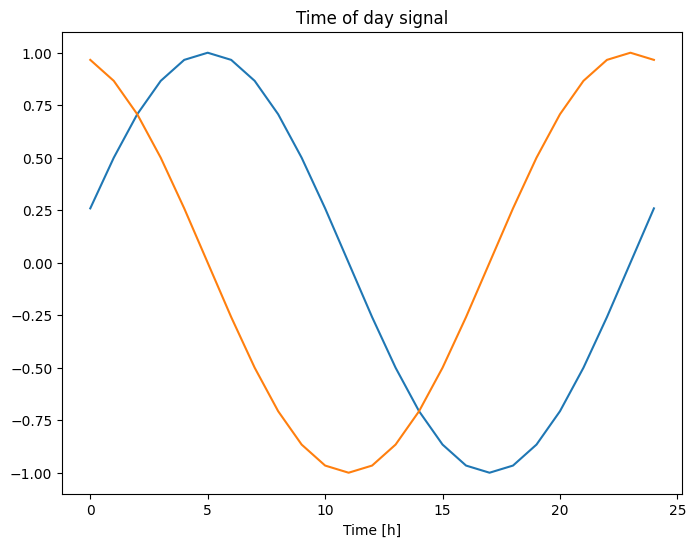
Điều này cho phép mô hình truy cập vào các tính năng tần số quan trọng nhất. Trong trường hợp này, bạn đã biết trước tần số nào là quan trọng.
Nếu bạn không có thông tin đó, bạn có thể xác định tần số nào là quan trọng bằng cách trích xuất các tính năng với Fast Fourier Transform . Để kiểm tra các giả định, đây là tf.signal.rfft của nhiệt độ theo thời gian. Lưu ý các đỉnh rõ ràng ở tần suất gần 1/year và 1/day :
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
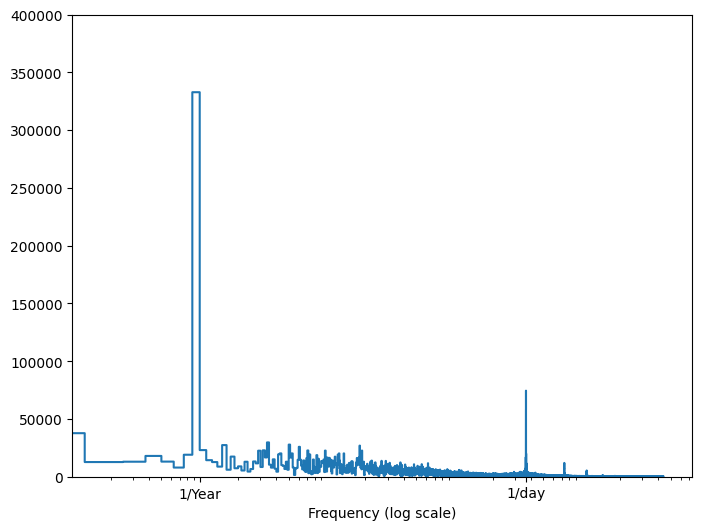
Tách dữ liệu
Bạn sẽ sử dụng phần chia (70%, 20%, 10%) cho các tập huấn luyện, xác thực và thử nghiệm. Lưu ý rằng dữ liệu không được xáo trộn ngẫu nhiên trước khi tách. Đây là vì hai lý do:
- Nó đảm bảo rằng việc cắt dữ liệu thành các cửa sổ của các mẫu liên tiếp vẫn có thể thực hiện được.
- Nó đảm bảo rằng kết quả xác nhận / kiểm tra thực tế hơn, được đánh giá dựa trên dữ liệu thu thập được sau khi mô hình được đào tạo.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
Chuẩn hóa dữ liệu
Điều quan trọng là phải mở rộng quy mô các tính năng trước khi đào tạo mạng nơ-ron. Chuẩn hóa là một cách phổ biến để thực hiện việc chia tỷ lệ này: trừ giá trị trung bình và chia cho độ lệch chuẩn của mỗi đối tượng địa lý.
Giá trị trung bình và độ lệch chuẩn chỉ nên được tính bằng cách sử dụng dữ liệu huấn luyện để các mô hình không có quyền truy cập vào các giá trị trong bộ kiểm tra và xác nhận.
Cũng có thể cho rằng mô hình không nên có quyền truy cập vào các giá trị tương lai trong tập huấn luyện khi huấn luyện và việc chuẩn hóa này nên được thực hiện bằng cách sử dụng các đường trung bình động. Đó không phải là trọng tâm của hướng dẫn này và các bộ xác nhận và kiểm tra đảm bảo rằng bạn nhận được (phần nào) các số liệu trung thực. Vì vậy, vì sự đơn giản, hướng dẫn này sử dụng một mức trung bình đơn giản.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
Bây giờ, hãy nhìn vào sự phân bố của các tính năng. Một số tính năng có đuôi dài, nhưng không có sai số rõ ràng như giá trị vận tốc gió -9999 .
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)

Cửa sổ dữ liệu
Các mô hình trong hướng dẫn này sẽ tạo một tập hợp các dự đoán dựa trên một cửa sổ các mẫu liên tiếp từ dữ liệu.
Các tính năng chính của cửa sổ nhập liệu là:
- Chiều rộng (số bước thời gian) của cửa sổ nhập và nhãn.
- Khoảng thời gian bù đắp giữa chúng.
- Những tính năng nào được sử dụng làm đầu vào, nhãn hoặc cả hai.
Hướng dẫn này xây dựng nhiều mô hình khác nhau (bao gồm mô hình Tuyến tính, DNN, CNN và RNN) và sử dụng chúng cho cả hai:
- Dự đoán một đầu ra và nhiều đầu ra .
- Dự đoán một bước thời gian và nhiều bước thời gian .
Phần này tập trung vào việc triển khai cửa sổ dữ liệu để nó có thể được sử dụng lại cho tất cả các mô hình đó.
Tùy thuộc vào nhiệm vụ và loại mô hình, bạn có thể muốn tạo nhiều cửa sổ dữ liệu khác nhau. Dưới đây là một số ví dụ:
Ví dụ: để đưa ra một dự đoán duy nhất trong 24 giờ tới trong tương lai, với 24 giờ lịch sử, bạn có thể xác định một cửa sổ như sau:
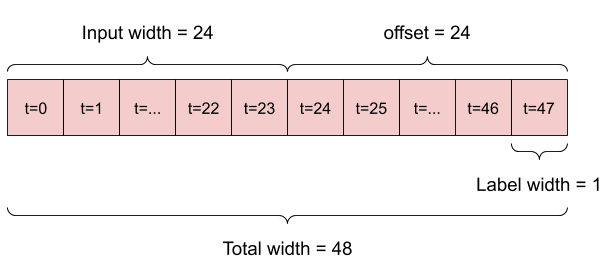
Một mô hình đưa ra dự đoán một giờ trong tương lai, với sáu giờ lịch sử, sẽ cần một cửa sổ như thế này:

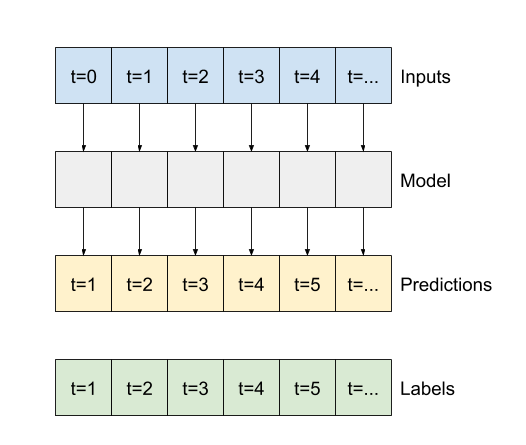
Phần còn lại của phần này định nghĩa một lớp WindowGenerator . Lớp này có thể:
- Xử lý các chỉ số và hiệu số như thể hiện trong sơ đồ trên.
- Chia cửa sổ của các đối tượng địa lý thành các cặp
(features, labels). - Vẽ nội dung của các cửa sổ kết quả.
- Tạo hiệu quả các lô cửa sổ này từ dữ liệu đào tạo, đánh giá và kiểm tra, sử dụng
tf.data.Datasets.
1. Chỉ số và hiệu số
Bắt đầu bằng cách tạo lớp WindowGenerator . Phương thức __init__ bao gồm tất cả logic cần thiết cho các chỉ số đầu vào và nhãn.
Nó cũng lấy việc đào tạo, đánh giá và kiểm tra DataFrames làm đầu vào. Chúng sẽ được chuyển đổi thành tf.data.Dataset của windows sau này.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
Đây là mã để tạo 2 cửa sổ được hiển thị trong sơ đồ ở đầu phần này:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. Tách
Đưa ra một danh sách các đầu vào liên tiếp, phương thức split_window sẽ chuyển đổi chúng thành một cửa sổ đầu vào và một cửa sổ nhãn.
Ví dụ w2 mà bạn xác định trước đó sẽ được chia như thế này:
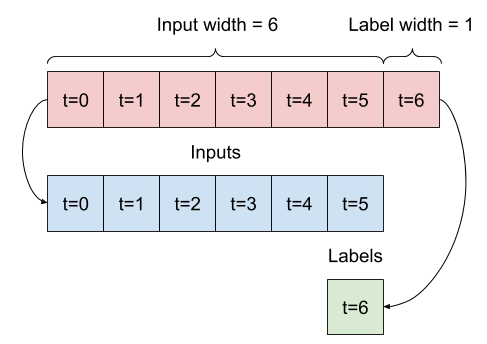
Biểu đồ này không hiển thị trục features của dữ liệu, nhưng hàm split_window này cũng xử lý label_columns để có thể sử dụng nó cho cả ví dụ đầu ra đơn và nhiều đầu ra.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
Hãy thử nó ra:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
Thông thường, dữ liệu trong TensorFlow được đóng gói thành các mảng trong đó chỉ mục ngoài cùng nằm trên các ví dụ (thứ nguyên "lô"). Các chỉ số ở giữa là (các) thứ nguyên "thời gian" hoặc "không gian" (chiều rộng, chiều cao). Các chỉ số trong cùng là các tính năng.
Đoạn mã trên lấy một loạt ba cửa sổ bước 7 thời gian với 19 tính năng ở mỗi bước thời gian. Nó chia chúng thành một loạt các đầu vào tính năng bước 19 lần 6 và nhãn tính năng bước 1 lần 1. Nhãn chỉ có một tính năng vì WindowGenerator được khởi tạo với label_columns=['T (degC)'] . Ban đầu, hướng dẫn này sẽ xây dựng các mô hình dự đoán các nhãn đầu ra đơn lẻ.
3. Cốt truyện
Đây là một phương pháp biểu đồ cho phép hình dung đơn giản về cửa sổ chia nhỏ:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
Biểu đồ này sắp xếp các đầu vào, nhãn và các dự đoán (sau này) dựa trên thời gian mục đề cập đến:
w2.plot()
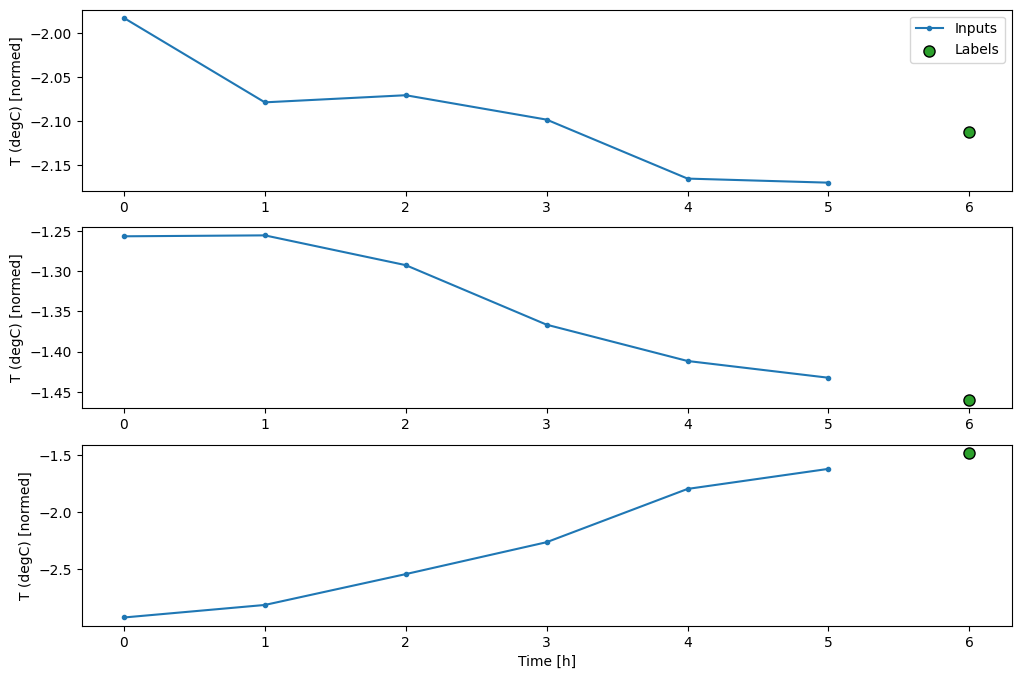
Bạn có thể vẽ biểu đồ cho các cột khác, nhưng cấu hình w2 của cửa sổ ví dụ chỉ có nhãn cho cột T (degC) .
w2.plot(plot_col='p (mbar)')
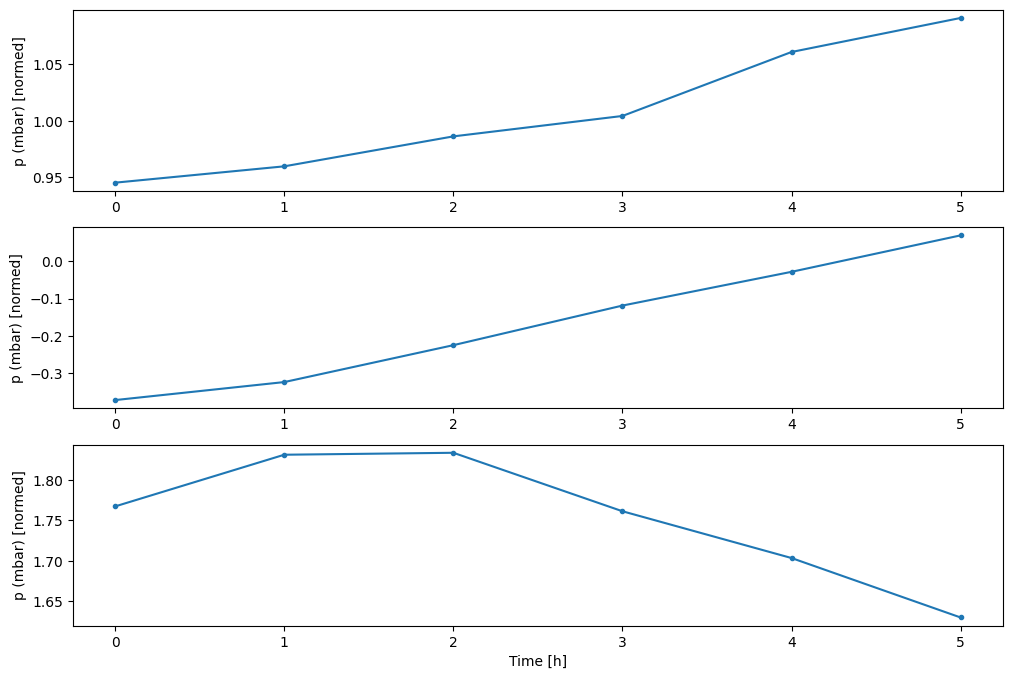
4. Tạo tf.data.Dataset s
Cuối cùng, phương thức make_dataset này sẽ sử dụng một chuỗi thời gian DataFrame và chuyển đổi nó thành một tf.data.Dataset của các cặp (input_window, label_window) bằng cách sử dụng hàm tf.keras.utils.timeseries_dataset_from_array :
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
Đối tượng WindowGenerator chứa dữ liệu huấn luyện, xác thực và thử nghiệm.
Thêm các thuộc tính để truy cập chúng dưới dạng tf.data.Dataset bằng cách sử dụng phương thức make_dataset mà bạn đã xác định trước đó. Ngoài ra, hãy thêm một lô ví dụ tiêu chuẩn để dễ dàng truy cập và vẽ biểu đồ:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
Bây giờ, đối tượng WindowGenerator cung cấp cho bạn quyền truy cập vào các đối tượng tf.data.Dataset , vì vậy bạn có thể dễ dàng lặp lại dữ liệu.
Thuộc tính Dataset.element_spec cho bạn biết cấu trúc, kiểu dữ liệu và hình dạng của các phần tử tập dữ liệu.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
Lặp lại trên Dataset sẽ tạo ra các lô cụ thể:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
Mô hình một bước
Mô hình đơn giản nhất mà bạn có thể xây dựng dựa trên loại dữ liệu này là mô hình dự đoán giá trị của một đối tượng địa lý — 1 bước thời gian (một giờ) trong tương lai chỉ dựa trên các điều kiện hiện tại.
Vì vậy, hãy bắt đầu bằng cách xây dựng các mô hình để dự đoán giá trị T (degC) trong một giờ tới trong tương lai.

Định cấu hình đối tượng WindowGenerator để tạo các cặp (input, label) một bước sau:
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
Đối tượng window tạo các tf.data.Dataset từ các tập huấn luyện, xác thực và kiểm tra, cho phép bạn dễ dàng lặp lại các lô dữ liệu.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
Đường cơ sở
Trước khi xây dựng một mô hình có thể đào tạo, tốt hơn là nên có một đường cơ sở hiệu suất làm điểm để so sánh với các mô hình phức tạp hơn sau này.
Nhiệm vụ đầu tiên này là dự đoán nhiệt độ một giờ trong tương lai, với giá trị hiện tại của tất cả các tính năng. Các giá trị hiện tại bao gồm nhiệt độ hiện tại.
Vì vậy, hãy bắt đầu với một mô hình chỉ trả về nhiệt độ hiện tại như dự đoán, dự đoán là "Không thay đổi". Đây là đường cơ sở hợp lý vì nhiệt độ thay đổi chậm. Tất nhiên, đường cơ sở này sẽ hoạt động kém hiệu quả hơn nếu bạn đưa ra dự đoán xa hơn trong tương lai.
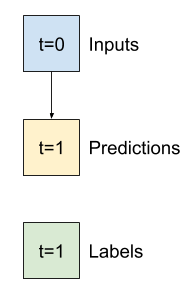
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
Khởi tạo và đánh giá mô hình này:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 2ms/step - loss: 0.0128 - mean_absolute_error: 0.0785
Điều đó đã in ra một số số liệu hiệu suất, nhưng những số liệu đó không cho bạn cảm giác về việc mô hình đang hoạt động tốt như thế nào.
WindowGenerator có một phương pháp cốt truyện, nhưng các âm mưu sẽ không thú vị lắm nếu chỉ có một mẫu duy nhất.
Vì vậy, hãy tạo WindowGenerator rộng hơn để tạo ra các cửa sổ 24 giờ liên tiếp các đầu vào và nhãn tại một thời điểm. Biến wide_window mới không thay đổi cách hoạt động của mô hình. Mô hình vẫn đưa ra dự đoán một giờ trong tương lai dựa trên một bước thời gian đầu vào duy nhất. Ở đây, trục time hoạt động giống như trục batch : mỗi dự đoán được thực hiện độc lập mà không có sự tương tác giữa các bước thời gian:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
Cửa sổ mở rộng này có thể được chuyển trực tiếp đến cùng một mô hình baseline mà không có bất kỳ thay đổi mã nào. Điều này có thể thực hiện được vì các đầu vào và nhãn có cùng số bước thời gian và đường cơ sở chỉ chuyển tiếp đầu vào đến đầu ra:
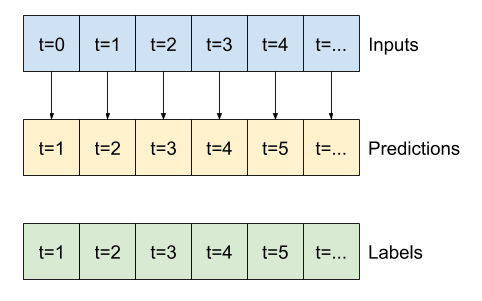
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
Bằng cách vẽ các dự đoán của mô hình cơ sở, hãy lưu ý rằng nó chỉ đơn giản là các nhãn dịch chuyển sang phải sau một giờ:
wide_window.plot(baseline)
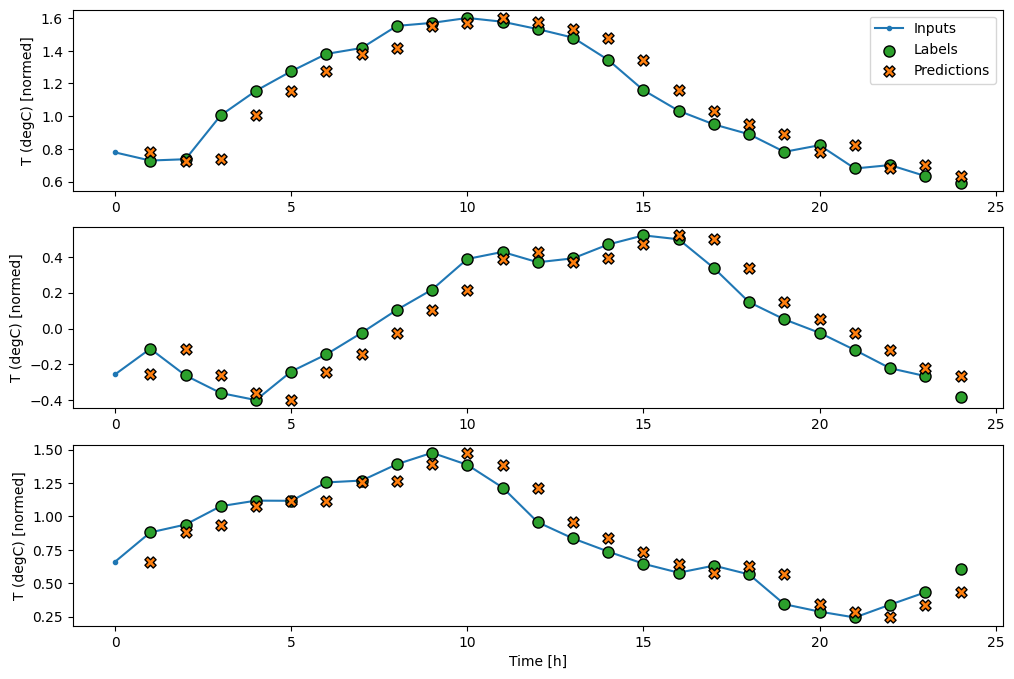
Trong ba ví dụ trên, mô hình một bước được chạy trong vòng 24 giờ. Điều này đáng được giải thích:
- Dòng
Inputsmàu xanh lam hiển thị nhiệt độ đầu vào tại mỗi bước thời gian. Mô hình nhận được tất cả các tính năng, biểu đồ này chỉ hiển thị nhiệt độ. - Các chấm
Labelsmàu xanh lá cây hiển thị giá trị dự đoán mục tiêu. Các dấu chấm này được hiển thị tại thời điểm dự đoán, không phải thời gian nhập liệu. Đó là lý do tại sao phạm vi nhãn được dịch chuyển 1 bậc so với đầu vào. - Dấu gạch chéo
Predictionsmàu cam là dự đoán của mô hình cho mỗi bước thời gian đầu ra. Nếu mô hình dự đoán hoàn hảo thì các dự đoán sẽ trực tiếp đến cácLabels.
Mô hình tuyến tính
Mô hình có thể đào tạo đơn giản nhất mà bạn có thể áp dụng cho tác vụ này là chèn phép biến đổi tuyến tính giữa đầu vào và đầu ra. Trong trường hợp này, kết quả từ một bước thời gian chỉ phụ thuộc vào bước đó:

Lớp tf.keras.layers.Dense không có tập hợp activation là một mô hình tuyến tính. Lớp chỉ chuyển đổi trục cuối cùng của dữ liệu từ (batch, time, inputs) thành (batch, time, units) ; nó được áp dụng độc lập cho mọi mặt hàng trên các trục time và batch .
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
Hướng dẫn này đào tạo nhiều mô hình, vì vậy hãy đóng gói quy trình đào tạo thành một hàm:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(),
metrics=[tf.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
Đào tạo mô hình và đánh giá hiệu suất của nó:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0586 - mean_absolute_error: 0.1659 - val_loss: 0.0135 - val_mean_absolute_error: 0.0858 Epoch 2/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0109 - mean_absolute_error: 0.0772 - val_loss: 0.0093 - val_mean_absolute_error: 0.0711 Epoch 3/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0092 - mean_absolute_error: 0.0704 - val_loss: 0.0088 - val_mean_absolute_error: 0.0690 Epoch 4/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0089 - val_mean_absolute_error: 0.0692 Epoch 5/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0088 - val_mean_absolute_error: 0.0685 Epoch 6/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0697 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 Epoch 7/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0698 - val_loss: 0.0087 - val_mean_absolute_error: 0.0680 Epoch 8/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0090 - mean_absolute_error: 0.0695 - val_loss: 0.0087 - val_mean_absolute_error: 0.0683 Epoch 9/20 1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 439/439 [==============================] - 1s 2ms/step - loss: 0.0087 - mean_absolute_error: 0.0684
Giống như mô hình baseline , mô hình tuyến tính có thể được gọi trên các lô cửa sổ rộng. Được sử dụng theo cách này, mô hình tạo một tập hợp các dự đoán độc lập trên các bước thời gian liên tiếp. Trục time hoạt động giống như một trục batch khác. Không có tương tác giữa các dự đoán tại mỗi bước thời gian.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
Dưới đây là sơ đồ các dự đoán ví dụ của nó trên wide_window , lưu ý rằng trong nhiều trường hợp, dự đoán rõ ràng tốt hơn so với việc chỉ trả lại nhiệt độ đầu vào, nhưng trong một số trường hợp, nó còn tệ hơn:
wide_window.plot(linear)
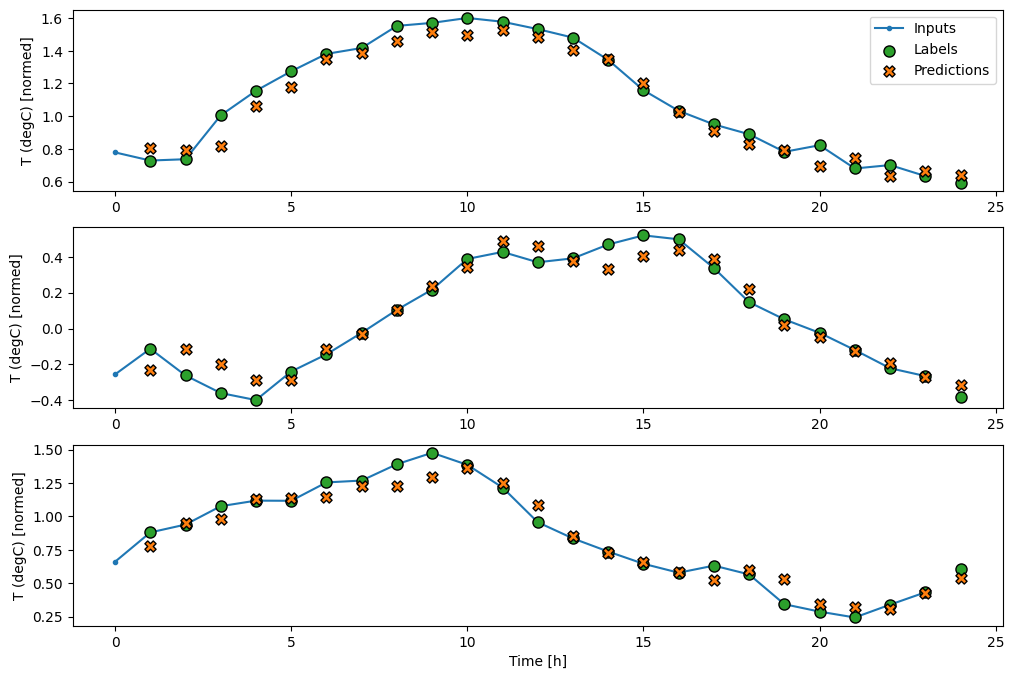
Một lợi thế của các mô hình tuyến tính là chúng tương đối đơn giản để giải thích. Bạn có thể kéo trọng số của lớp ra và hình dung trọng lượng được chỉ định cho mỗi đầu vào:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
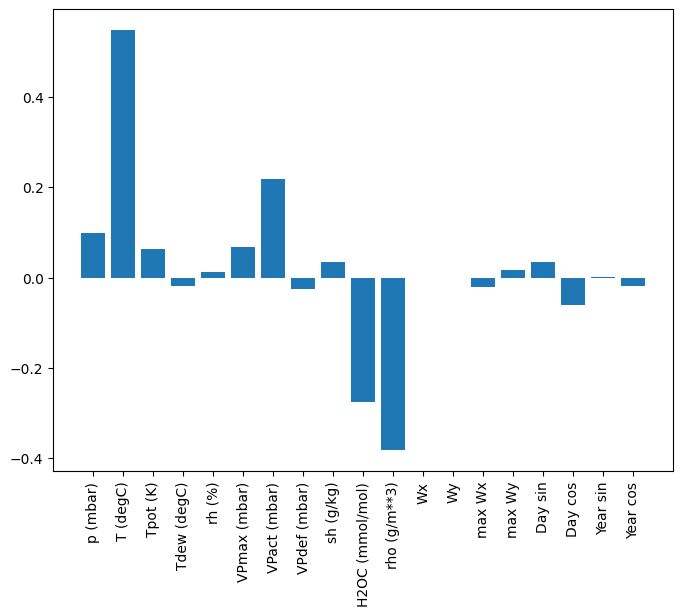
Đôi khi mô hình thậm chí không đặt trọng lượng lớn nhất lên đầu vào T (degC) . Đây là một trong những rủi ro của việc khởi tạo ngẫu nhiên.
Ngu độn
Trước khi áp dụng các mô hình thực sự hoạt động trên nhiều bước thời gian, bạn nên kiểm tra hiệu suất của các mô hình bước đầu vào đơn sâu hơn, mạnh mẽ hơn.
Đây là một mô hình tương tự như mô hình linear , ngoại trừ nó xếp chồng một vài lớp Dense giữa đầu vào và đầu ra:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
Epoch 1/20 1534/1534 [==============================] - 7s 4ms/step - loss: 0.0132 - mean_absolute_error: 0.0779 - val_loss: 0.0081 - val_mean_absolute_error: 0.0666 Epoch 2/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0652 - val_loss: 0.0073 - val_mean_absolute_error: 0.0610 Epoch 3/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0076 - mean_absolute_error: 0.0627 - val_loss: 0.0072 - val_mean_absolute_error: 0.0618 Epoch 4/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0609 - val_loss: 0.0068 - val_mean_absolute_error: 0.0582 Epoch 5/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0581 Epoch 6/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0594 - val_loss: 0.0067 - val_mean_absolute_error: 0.0579 Epoch 7/20 1534/1534 [==============================] - 6s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0590 - val_loss: 0.0068 - val_mean_absolute_error: 0.0580 439/439 [==============================] - 1s 3ms/step - loss: 0.0068 - mean_absolute_error: 0.0580
Nhiều bước dày đặc
Mô hình một bước thời gian không có ngữ cảnh cho các giá trị hiện tại của các đầu vào của nó. Nó không thể thấy các tính năng đầu vào thay đổi như thế nào theo thời gian. Để giải quyết vấn đề này, mô hình cần truy cập vào nhiều bước thời gian khi đưa ra dự đoán:
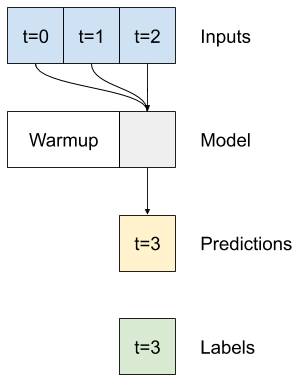
Các mô hình baseline , linear và dense xử lý từng bước thời gian một cách độc lập. Ở đây mô hình sẽ thực hiện nhiều bước thời gian làm đầu vào để tạo ra một đầu ra duy nhất.
Tạo WindowGenerator sẽ tạo ra các lô đầu vào dài ba giờ và nhãn một giờ:
Lưu ý rằng tham số shift của Window có liên quan đến phần cuối của hai cửa sổ.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
conv_window.plot()
plt.title("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 1.0, 'Given 3 hours of inputs, predict 1 hour into the future.')
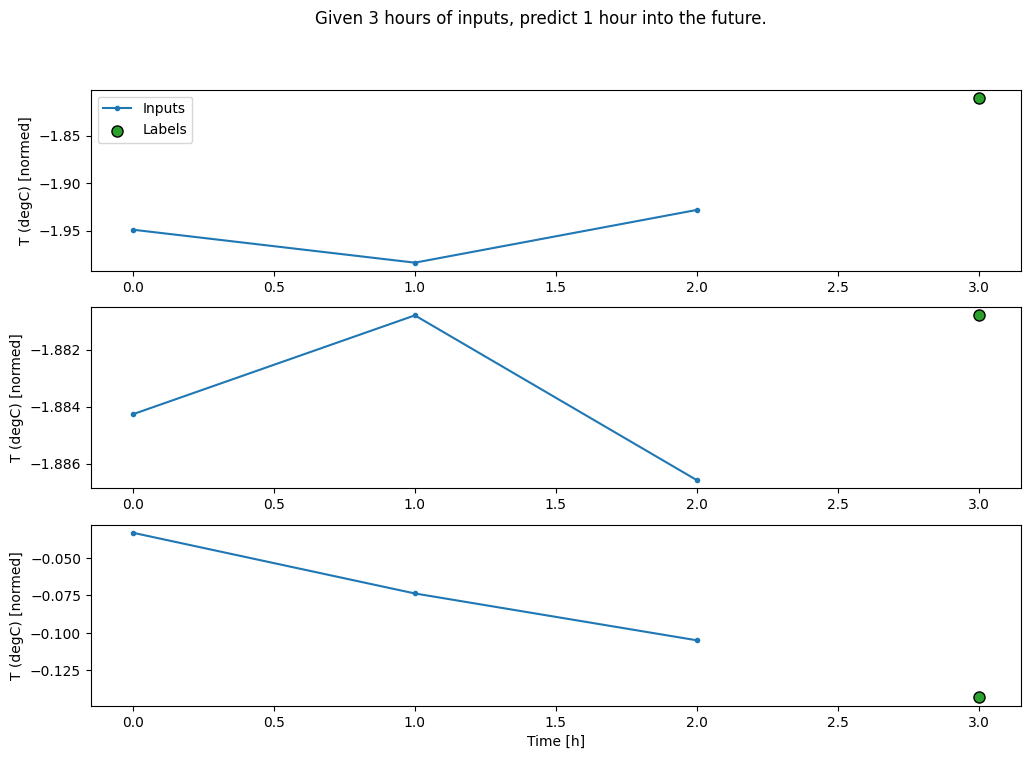
Bạn có thể đào tạo một mô hình dense trên cửa sổ nhiều bước đầu vào bằng cách thêm tf.keras.layers.Flatten làm lớp đầu tiên của mô hình:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0070 - mean_absolute_error: 0.0609
conv_window.plot(multi_step_dense)
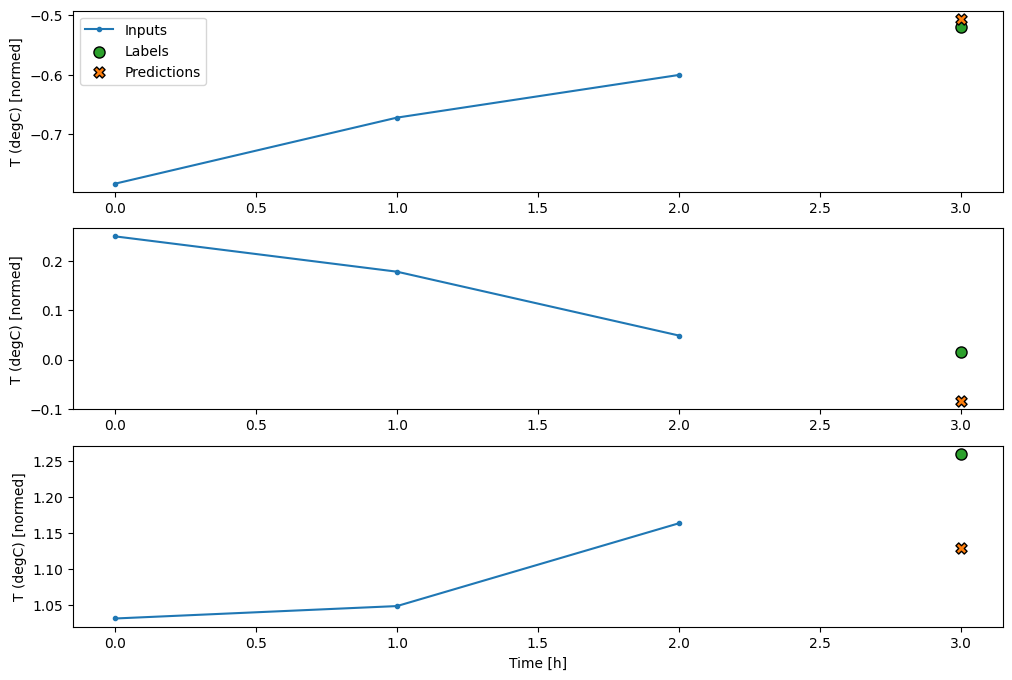
Mặt trái chính của phương pháp này là mô hình kết quả chỉ có thể được thực thi trên các cửa sổ đầu vào có chính xác hình dạng này.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling layer "sequential_2" (type Sequential). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Call arguments received: • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
Các mô hình tích chập trong phần tiếp theo sẽ khắc phục sự cố này.
Mạng nơ-ron chuyển đổi
Một lớp tích chập ( tf.keras.layers.Conv1D ) cũng có nhiều bước thời gian làm đầu vào cho mỗi dự đoán.
Dưới đây là mô hình tương tự như multi_step_dense , được viết lại bằng một tích chập.
Lưu ý những thay đổi:
- Các
tf.keras.layers.Flattenvàtf.keras.layers.Denseđầu tiên được thay thế bằngtf.keras.layers.Conv1D. -
tf.keras.layers.Reshapekhông còn cần thiết vì tích chập giữ trục thời gian trong đầu ra của nó.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
Chạy nó trên một lô ví dụ để kiểm tra xem mô hình có tạo ra kết quả đầu ra với hình dạng mong đợi hay không:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
Đào tạo và đánh giá nó trên kênh chuyển đổi và nó sẽ cung cấp hiệu suất tương tự multi_step_dense conv_window
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0063 - mean_absolute_error: 0.0568
Sự khác biệt giữa mô hình multi_step_dense conv_model mô hình conv_model có thể được chạy trên các đầu vào có độ dài bất kỳ. Lớp phức hợp được áp dụng cho một cửa sổ trượt của các đầu vào:
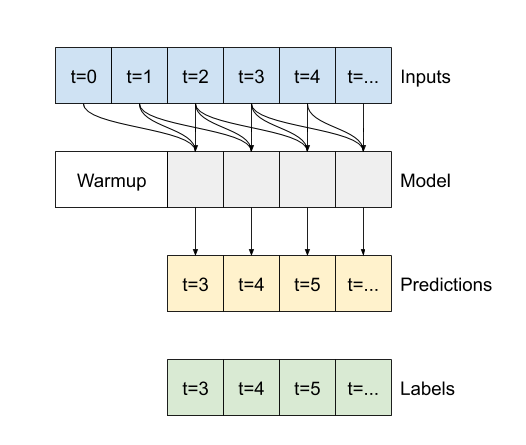
Nếu bạn chạy nó trên đầu vào rộng hơn, nó sẽ tạo ra đầu ra rộng hơn:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1)
Lưu ý rằng đầu ra ngắn hơn đầu vào. Để làm cho việc đào tạo hoặc lập kế hoạch hoạt động, bạn cần các nhãn và dự đoán có cùng độ dài. Vì vậy, hãy xây dựng WindowGenerator để tạo ra các cửa sổ rộng với một vài bước thời gian nhập bổ sung để độ dài nhãn và dự đoán khớp với nhau:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1)
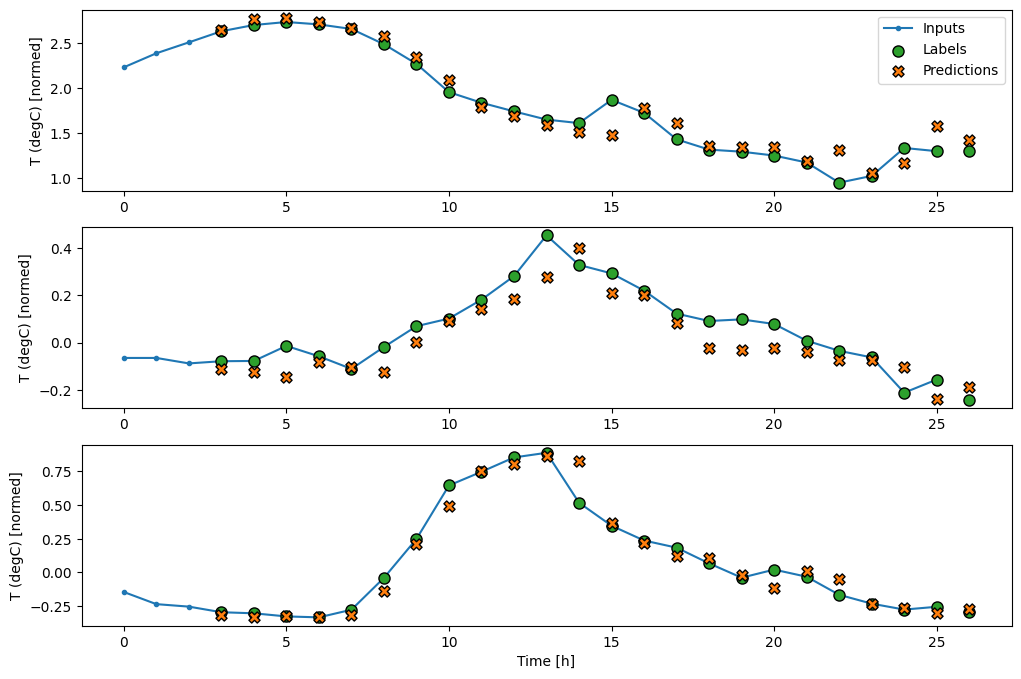
Bây giờ, bạn có thể vẽ các dự đoán của mô hình trên một cửa sổ rộng hơn. Lưu ý 3 bước thời gian nhập liệu trước lần dự đoán đầu tiên. Mọi dự đoán ở đây đều dựa trên 3 bước thời gian trước đó:
wide_conv_window.plot(conv_model)
Mạng nơ-ron lặp lại
Mạng nơ-ron tuần hoàn (RNN) là một loại mạng nơ-ron rất phù hợp với dữ liệu chuỗi thời gian. RNN xử lý chuỗi thời gian từng bước, duy trì trạng thái bên trong từ bước thời gian này sang bước thời gian.
Bạn có thể tìm hiểu thêm trong phần Tạo văn bản với hướng dẫn RNN và hướng dẫn Mạng thần kinh tái tạo (RNN) với hướng dẫn Keras .
Trong hướng dẫn này, bạn sẽ sử dụng một lớp RNN có tên là Bộ nhớ ngắn hạn dài ( tf.keras.layers.LSTM ).
Đối số phương thức khởi tạo quan trọng cho tất cả các lớp Keras RNN, chẳng hạn như tf.keras.layers.LSTM , là đối số return_sequences . Cài đặt này có thể định cấu hình lớp theo một trong hai cách:
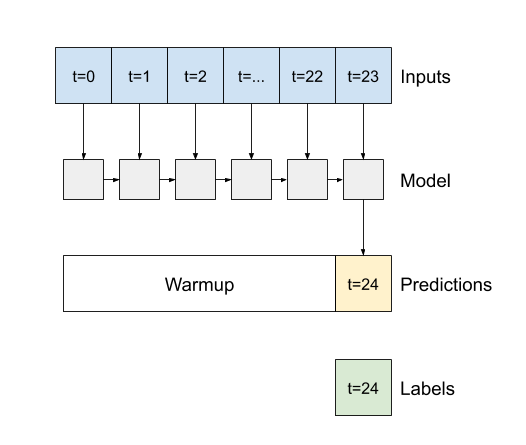
- Nếu là
False, theo mặc định, lớp chỉ trả về kết quả của bước thời gian cuối cùng, cho phép mô hình có thời gian để làm ấm trạng thái bên trong của nó trước khi đưa ra một dự đoán duy nhất:
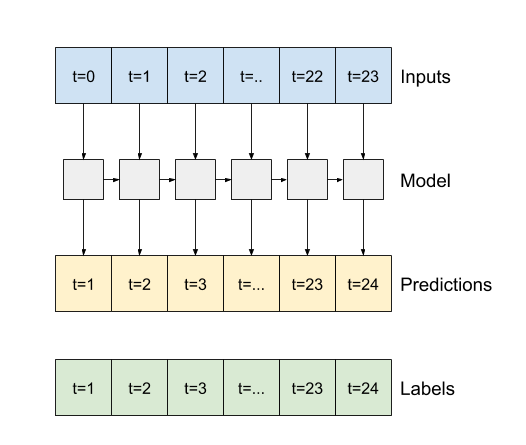
- Nếu
True, lớp trả về một đầu ra cho mỗi đầu vào. Điều này hữu ích cho:- Xếp chồng các lớp RNN.
- Đào tạo một mô hình trên nhiều bước thời gian đồng thời.
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
Với return_sequences=True , mô hình có thể được đào tạo dựa trên dữ liệu 24 giờ tại một thời điểm.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 3ms/step - loss: 0.0055 - mean_absolute_error: 0.0509
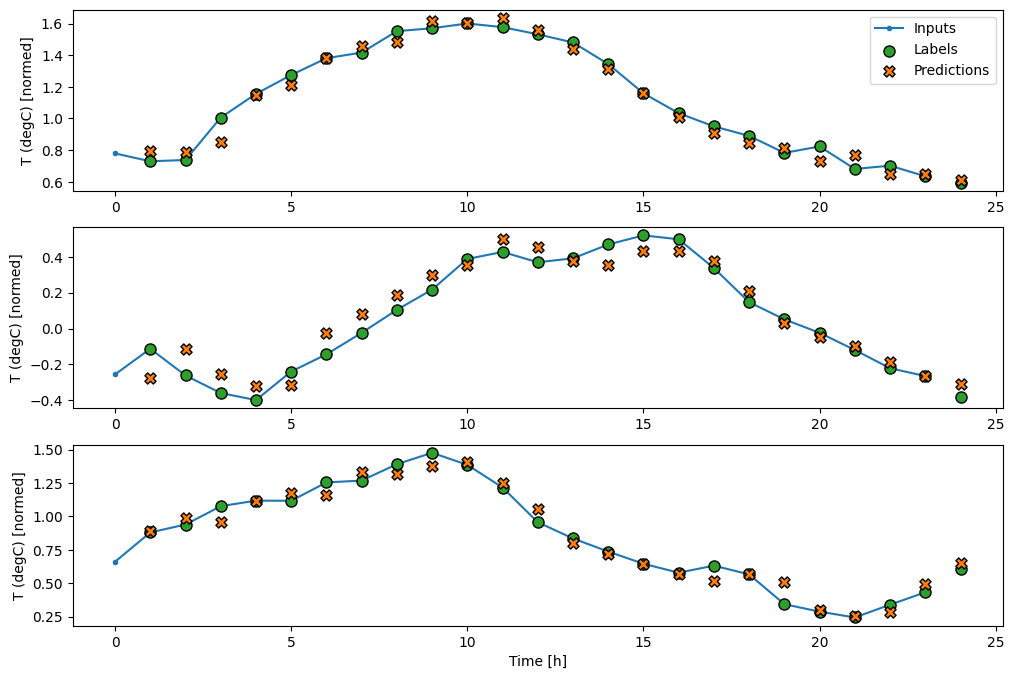
wide_window.plot(lstm_model)
Màn biểu diễn
Với tập dữ liệu này, mỗi mô hình thường hoạt động tốt hơn một chút so với tập dữ liệu trước đó:
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()
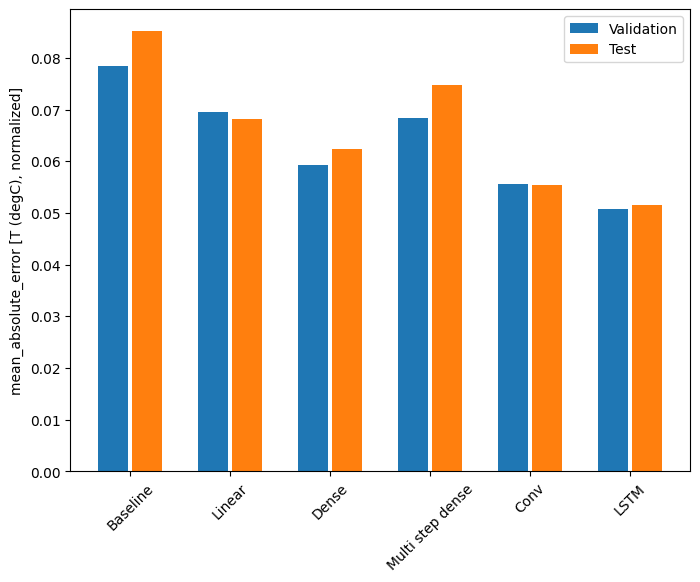
for name, value in performance.items():
print(f'{name:12s}: {value[1]:0.4f}')
Baseline : 0.0852 Linear : 0.0666 Dense : 0.0573 Multi step dense: 0.0586 Conv : 0.0577 LSTM : 0.0518
Các mô hình nhiều đầu ra
Các mô hình cho đến nay đều dự đoán một tính năng đầu ra duy nhất, T (degC) , cho một bước thời gian duy nhất.
Tất cả các mô hình này có thể được chuyển đổi để dự đoán nhiều tính năng chỉ bằng cách thay đổi số lượng đơn vị trong lớp đầu ra và điều chỉnh cửa sổ đào tạo để bao gồm tất cả các tính năng trong labels ( example_labels ):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
Lưu ý ở trên rằng trục features của các nhãn hiện có cùng độ sâu với các đầu vào, thay vì 1 .
Đường cơ sở
Có thể sử dụng cùng một mô hình đường cơ sở ( Baseline ) ở đây, nhưng lần này lặp lại tất cả các tính năng thay vì chọn một label_index cụ thể:
baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)
438/438 [==============================] - 1s 2ms/step - loss: 0.0886 - mean_absolute_error: 0.1589
Ngu độn
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)
439/439 [==============================] - 1s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1302
RNN
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0617 - mean_absolute_error: 0.1205 CPU times: user 5min 14s, sys: 1min 17s, total: 6min 31s Wall time: 2min 8s
Nâng cao: Kết nối dư
Mô hình Baseline trước đó đã tận dụng lợi thế của thực tế là trình tự không thay đổi đáng kể theo từng bước thời gian. Mọi mô hình được đào tạo trong hướng dẫn này cho đến nay đều được khởi tạo ngẫu nhiên và sau đó phải biết rằng kết quả đầu ra là một thay đổi nhỏ so với bước thời gian trước đó.
Mặc dù bạn có thể giải quyết vấn đề này bằng cách khởi tạo cẩn thận, nhưng việc xây dựng điều này vào cấu trúc mô hình sẽ đơn giản hơn.
Thông thường trong phân tích chuỗi thời gian để xây dựng các mô hình thay vì dự đoán giá trị tiếp theo, hãy dự đoán giá trị sẽ thay đổi như thế nào trong bước thời gian tiếp theo. Tương tự, các mạng dư —hoặc ResNets — trong học sâu đề cập đến các kiến trúc trong đó mỗi lớp thêm vào kết quả tích lũy của mô hình.
Đó là cách bạn tận dụng kiến thức rằng sự thay đổi chỉ nên nhỏ.
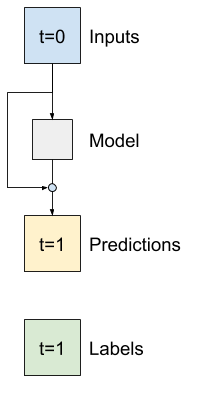
Về cơ bản, điều này khởi tạo mô hình để phù hợp với Baseline . Đối với nhiệm vụ này, nó giúp các mô hình hội tụ nhanh hơn, với hiệu suất tốt hơn một chút.
Cách tiếp cận này có thể được sử dụng kết hợp với bất kỳ mô hình nào được thảo luận trong hướng dẫn này.
Ở đây, nó đang được áp dụng cho mô hình LSTM, lưu ý việc sử dụng tf.initializers.zeros để đảm bảo rằng các thay đổi được dự đoán ban đầu là nhỏ và không chế ngự kết nối còn lại. Không có mối quan tâm về phá vỡ đối xứng đối với các gradient ở đây, vì các zeros chỉ được sử dụng trên lớp cuối cùng.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()
438/438 [==============================] - 1s 3ms/step - loss: 0.0620 - mean_absolute_error: 0.1179 CPU times: user 1min 43s, sys: 26.1 s, total: 2min 9s Wall time: 43.1 s
Màn biểu diễn
Đây là hiệu suất tổng thể cho các mô hình đa đầu ra này.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
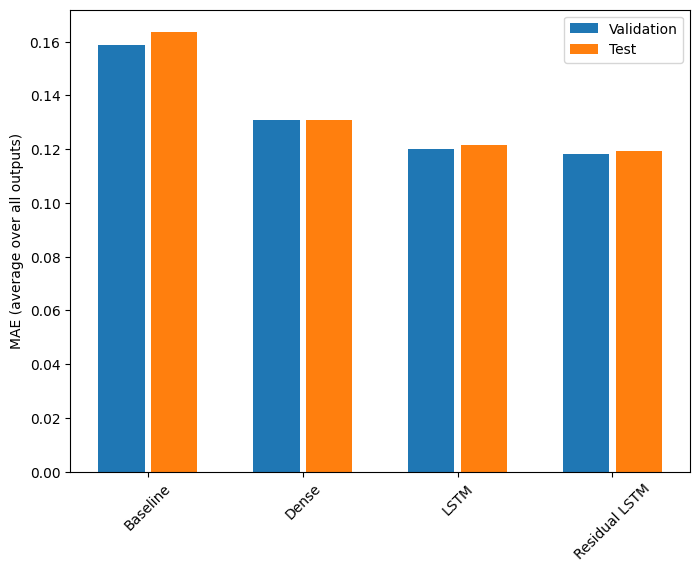
for name, value in performance.items():
print(f'{name:15s}: {value[1]:0.4f}')
Baseline : 0.1638 Dense : 0.1311 LSTM : 0.1214 Residual LSTM : 0.1194
Các hiệu suất trên được tính trung bình trên tất cả các đầu ra của mô hình.
Mô hình nhiều bước
Cả mô hình một đầu ra và nhiều đầu ra trong các phần trước đều đưa ra các dự đoán về bước thời gian duy nhất , một giờ nữa trong tương lai.
Phần này xem xét cách mở rộng các mô hình này để đưa ra dự đoán nhiều bước thời gian .
Trong dự đoán nhiều bước, mô hình cần học cách dự đoán một loạt các giá trị trong tương lai. Do đó, không giống như mô hình một bước, trong đó chỉ dự đoán một điểm duy nhất trong tương lai, mô hình nhiều bước dự đoán một chuỗi các giá trị trong tương lai.
Có hai cách tiếp cận cơ bản để giải quyết vấn đề này:
- Dự đoán một lần chụp trong đó toàn bộ chuỗi thời gian được dự đoán cùng một lúc.
- Dự đoán tự động hồi phục trong đó mô hình chỉ đưa ra dự đoán từng bước và đầu ra của nó được đưa trở lại làm đầu vào của nó.
Trong phần này, tất cả các mô hình sẽ dự đoán tất cả các tính năng trên tất cả các bước thời gian đầu ra .
Đối với mô hình nhiều bước, dữ liệu đào tạo lại bao gồm các mẫu hàng giờ. Tuy nhiên, ở đây, các mô hình sẽ học cách dự đoán 24 giờ trong tương lai, cho 24 giờ trong quá khứ.
Đây là một đối tượng Window tạo ra các lát này từ tập dữ liệu:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
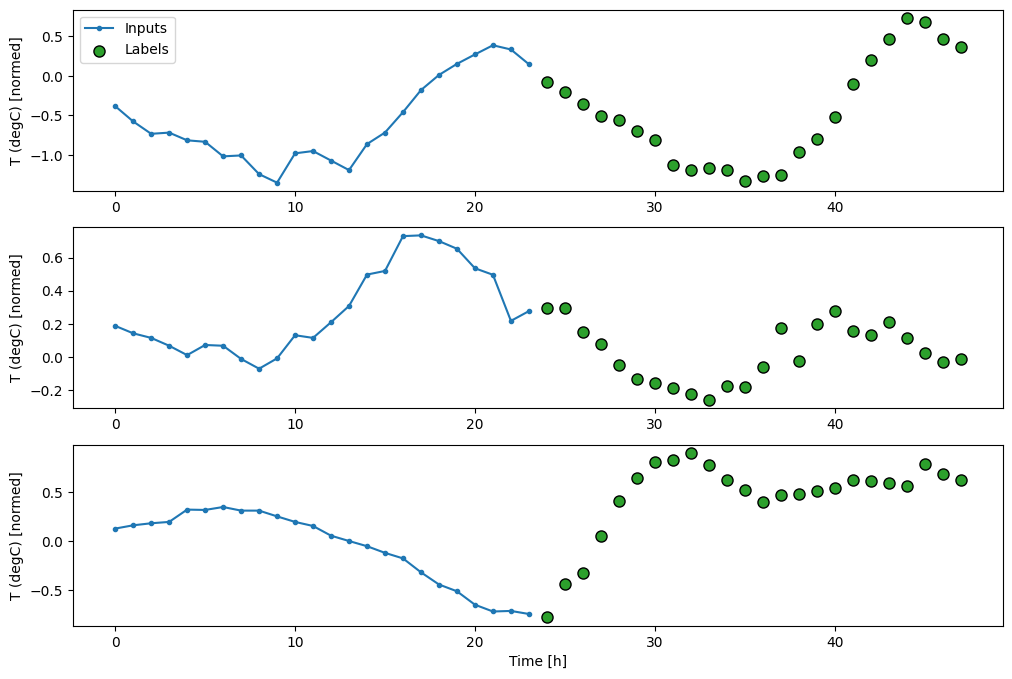
Đường cơ sở
Một cơ sở đơn giản cho tác vụ này là lặp lại bước thời gian đầu vào cuối cùng cho số bước thời gian đầu ra được yêu cầu:
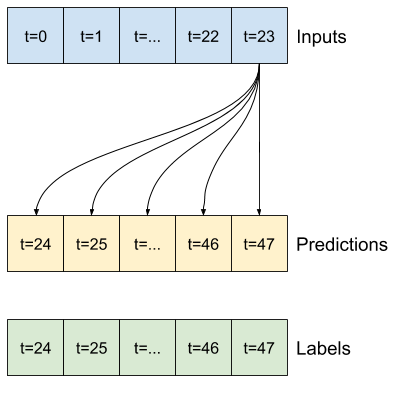
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(last_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.6285 - mean_absolute_error: 0.5007
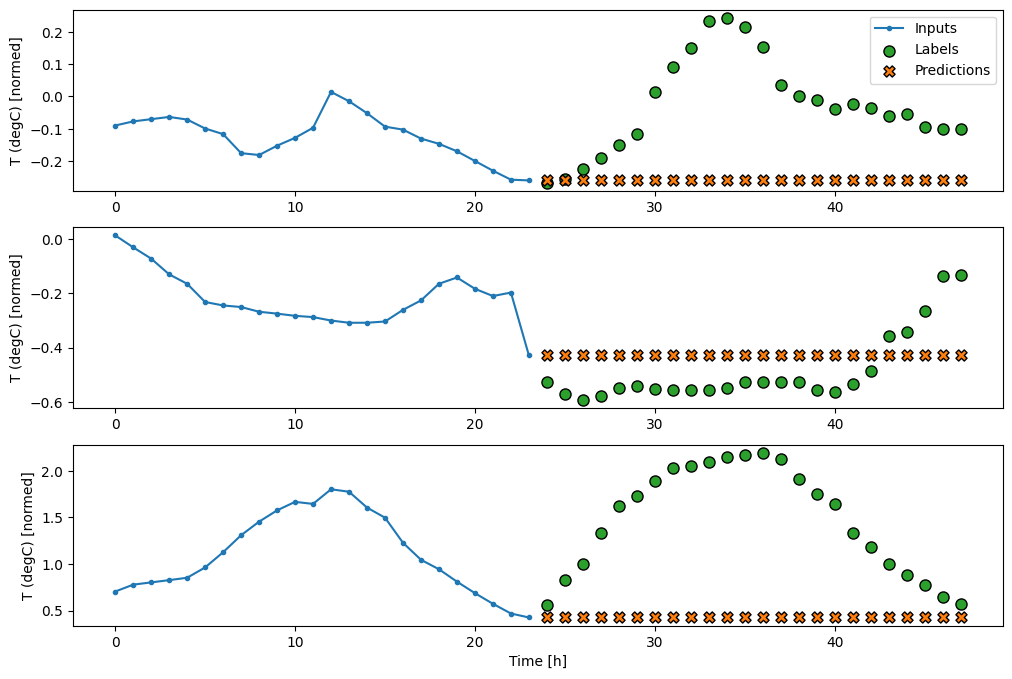
Vì nhiệm vụ này là dự đoán 24 giờ trong tương lai, cho 24 giờ trong quá khứ, nên một cách tiếp cận đơn giản khác là lặp lại ngày trước đó, giả sử ngày mai sẽ tương tự:
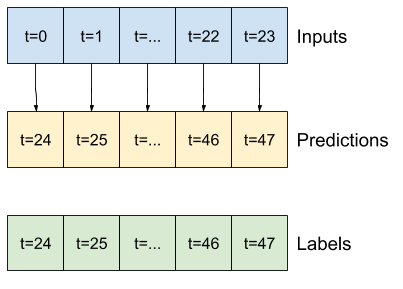
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.losses.MeanSquaredError(),
metrics=[tf.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0)
multi_window.plot(repeat_baseline)
437/437 [==============================] - 1s 2ms/step - loss: 0.4270 - mean_absolute_error: 0.3959
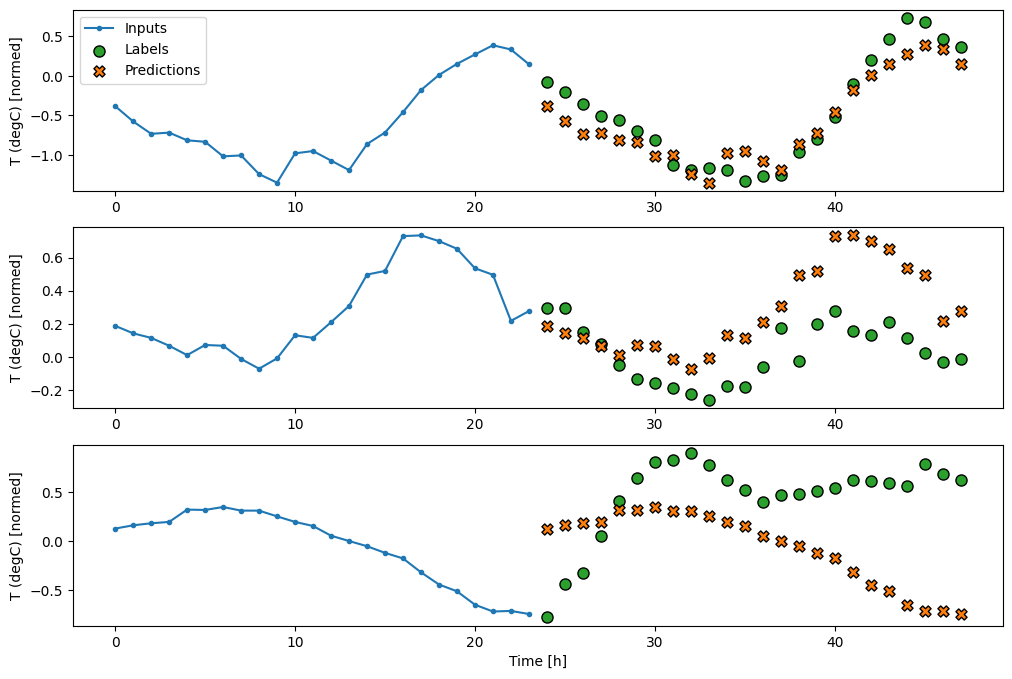
Các kiểu chụp đơn
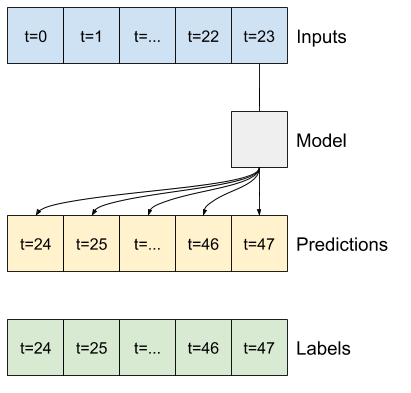
Một cách tiếp cận cấp cao cho vấn đề này là sử dụng mô hình "một lần chụp", trong đó mô hình đưa ra dự đoán toàn bộ trình tự trong một bước duy nhất.
Điều này có thể được triển khai hiệu quả dưới dạng tf.keras.layers.Dense với các đơn vị đầu ra OUT_STEPS*features . Mô hình chỉ cần định hình lại đầu ra đó theo yêu cầu (OUTPUT_STEPS, features) .
Tuyến tính
Mô hình tuyến tính đơn giản dựa trên bước thời gian đầu vào cuối cùng hoạt động tốt hơn so với một trong hai mô hình cơ sở, nhưng kém hiệu quả. Mô hình cần dự đoán các bước thời gian OUTPUT_STEPS , từ một bước thời gian đầu vào duy nhất với phép chiếu tuyến tính. Nó chỉ có thể ghi lại một phần hành vi có chiều hướng thấp, có thể chủ yếu dựa vào thời gian trong ngày và thời gian trong năm.
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_linear_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2559 - mean_absolute_error: 0.3053
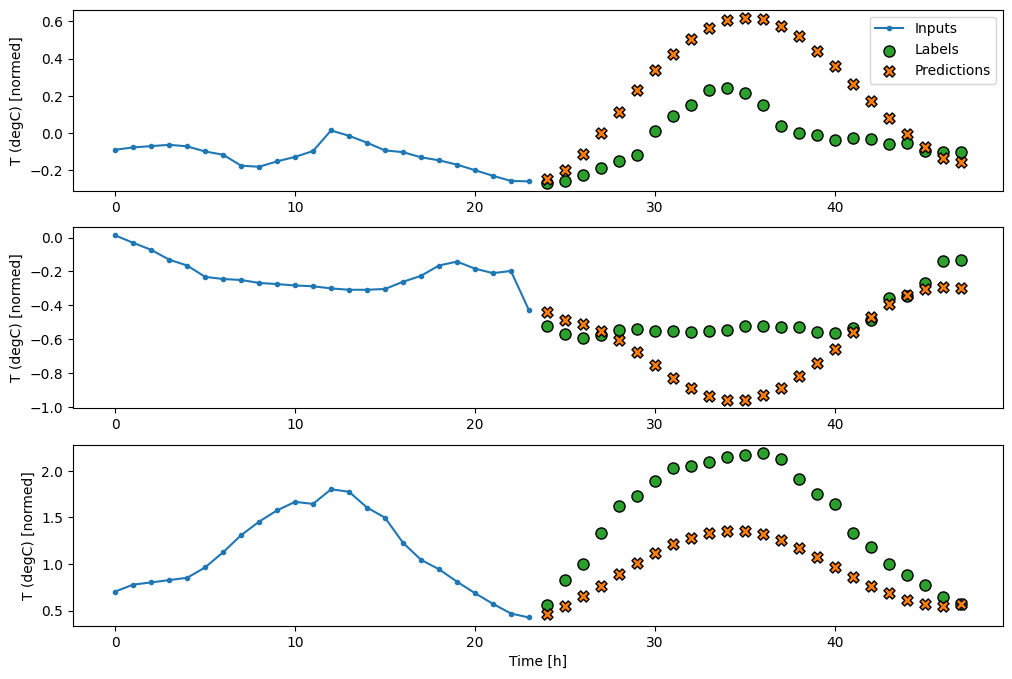
Ngu độn
Việc thêm tf.keras.layers.Dense giữa đầu vào và đầu ra mang lại cho mô hình tuyến tính nhiều năng lượng hơn, nhưng vẫn chỉ dựa trên một bước thời gian đầu vào duy nhất.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_dense_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2205 - mean_absolute_error: 0.2837
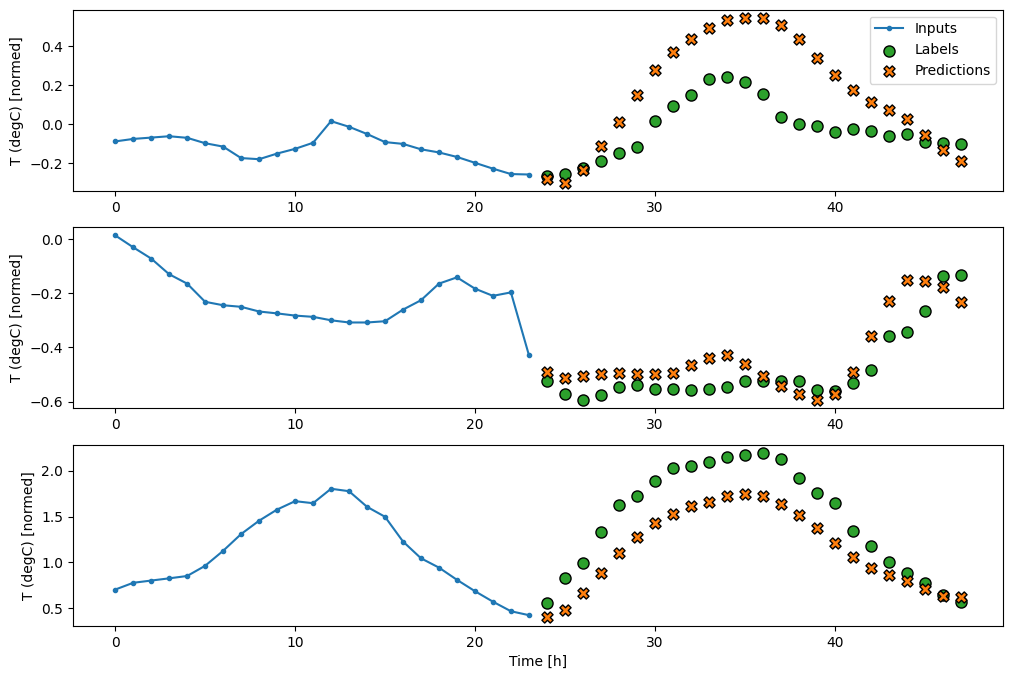
CNN
Mô hình tích hợp đưa ra các dự đoán dựa trên lịch sử có chiều rộng cố định, có thể dẫn đến hiệu suất tốt hơn so với mô hình dày đặc vì nó có thể thấy mọi thứ đang thay đổi như thế nào theo thời gian:
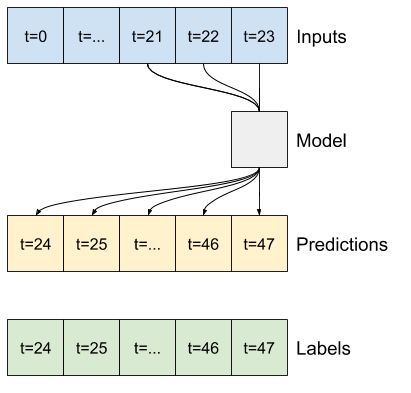
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_conv_model)
437/437 [==============================] - 1s 2ms/step - loss: 0.2158 - mean_absolute_error: 0.2833
RNN
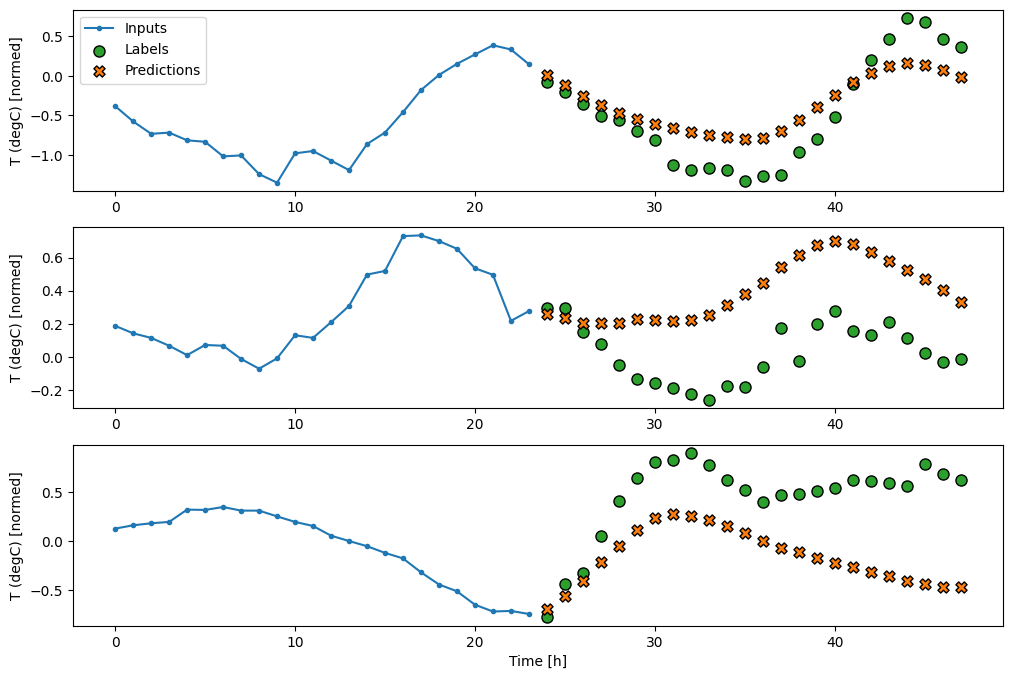
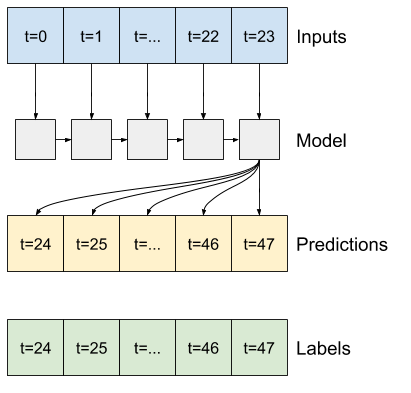
Một mô hình lặp lại có thể học cách sử dụng lịch sử lâu dài của các đầu vào, nếu nó có liên quan đến các dự đoán mà mô hình đang đưa ra. Tại đây, mô hình sẽ tích lũy trạng thái bên trong trong 24 giờ, trước khi đưa ra một dự đoán duy nhất trong 24 giờ tiếp theo.
Ở định dạng chụp một lần này, LSTM chỉ cần tạo ra một đầu ra ở bước thời gian cuối cùng, vì vậy hãy đặt return_sequences=False trong tf.keras.layers.LSTM .
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0)
multi_window.plot(multi_lstm_model)
437/437 [==============================] - 1s 3ms/step - loss: 0.2159 - mean_absolute_error: 0.2863
Nâng cao: Mô hình tự động hồi phục
Các mô hình trên đều dự đoán toàn bộ chuỗi đầu ra trong một bước duy nhất.
Trong một số trường hợp, mô hình có thể hữu ích khi phân tách dự đoán này thành các bước thời gian riêng lẻ. Sau đó, đầu ra của mỗi mô hình có thể được đưa trở lại chính nó ở mỗi bước và các dự đoán có thể được thực hiện với điều kiện trước đó, giống như trong Tạo chuỗi cổ điển với mạng thần kinh tái tạo .
Một ưu điểm rõ ràng của kiểu mô hình này là nó có thể được thiết lập để tạo ra đầu ra với độ dài khác nhau.
Bạn có thể thực hiện bất kỳ mô hình đa đầu ra đơn bước nào được đào tạo trong nửa đầu của hướng dẫn này và chạy trong vòng phản hồi tự động hồi phục, nhưng ở đây bạn sẽ tập trung vào việc xây dựng một mô hình đã được đào tạo rõ ràng để làm điều đó.
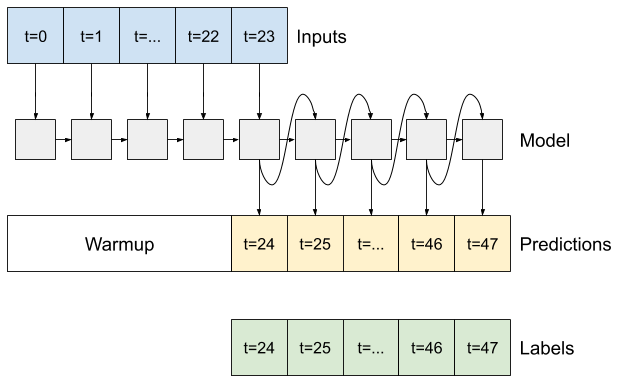
RNN
Hướng dẫn này chỉ xây dựng mô hình RNN tự động hồi phục, nhưng mô hình này có thể được áp dụng cho bất kỳ mô hình nào được thiết kế để xuất ra một bước thời gian duy nhất.
Mô hình sẽ có dạng cơ bản giống như các mô hình LSTM một bước trước đó: một lớp tf.keras.layers.LSTM tiếp theo là một lớp tf.keras.layers.Dense chuyển đổi đầu ra của lớp LSTM thành các dự đoán của mô hình.
Một tf.keras.layers.LSTM là một tf.keras.layers.LSTMCell được bao bọc trong tf.keras.layers.RNN cấp cao hơn để quản lý trạng thái và kết quả trình tự cho bạn (Kiểm tra Mạng thần kinh hiện tại (RNN) với Keras hướng dẫn chi tiết).
Trong trường hợp này, mô hình phải quản lý thủ công các đầu vào cho từng bước, vì vậy nó sử dụng tf.keras.layers.LSTMCell trực tiếp cho giao diện bước thời gian đơn, cấp thấp hơn.
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
Phương pháp đầu tiên mà mô hình này cần là warmup pháp khởi động để khởi tạo trạng thái bên trong của nó dựa trên các đầu vào. Sau khi được đào tạo, trạng thái này sẽ nắm bắt các phần liên quan của lịch sử đầu vào. Điều này tương đương với mô hình LSTM một bước trước đó:
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
Phương thức này trả về một dự đoán bước thời gian duy nhất và trạng thái bên trong của LSTM :
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
Với trạng thái của RNN và dự đoán ban đầu, giờ đây bạn có thể tiếp tục lặp lại mô hình cung cấp các dự đoán ở mỗi bước trở lại làm đầu vào.
Cách tiếp cận đơn giản nhất để thu thập các dự đoán đầu ra là sử dụng một danh sách Python và một tf.stack sau vòng lặp.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
Chạy thử mô hình này trên các đầu vào ví dụ:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
Bây giờ, đào tạo mô hình:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0)
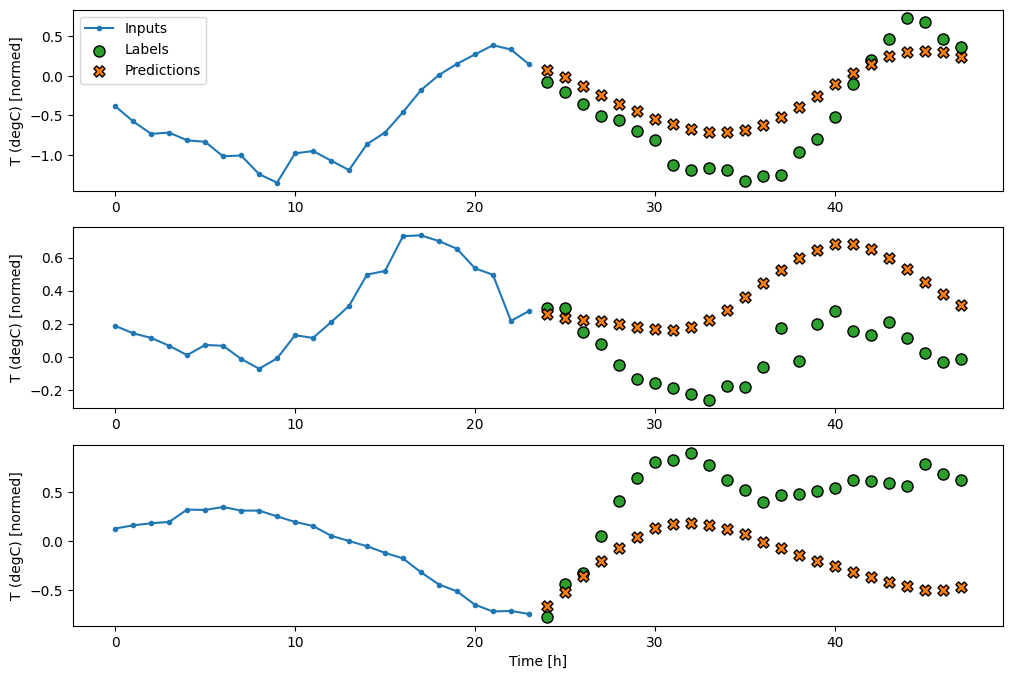
multi_window.plot(feedback_model)
437/437 [==============================] - 3s 8ms/step - loss: 0.2269 - mean_absolute_error: 0.3011
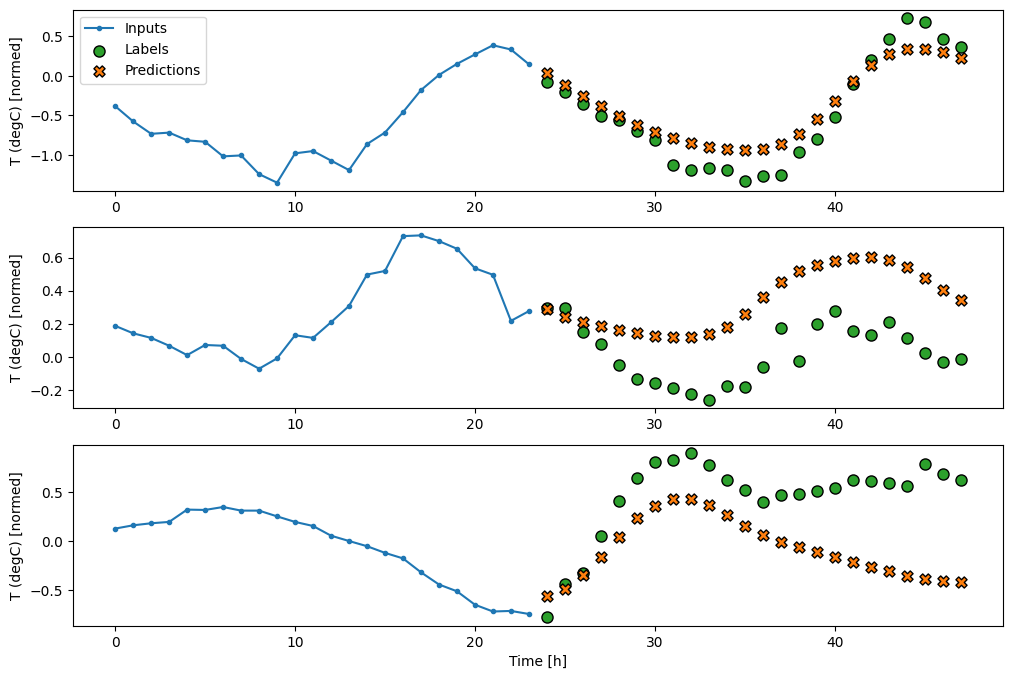
Màn biểu diễn
Có lợi nhuận giảm dần rõ ràng là một hàm của độ phức tạp của mô hình trong vấn đề này:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in multi_val_performance.values()]
test_mae = [v[metric_index] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()
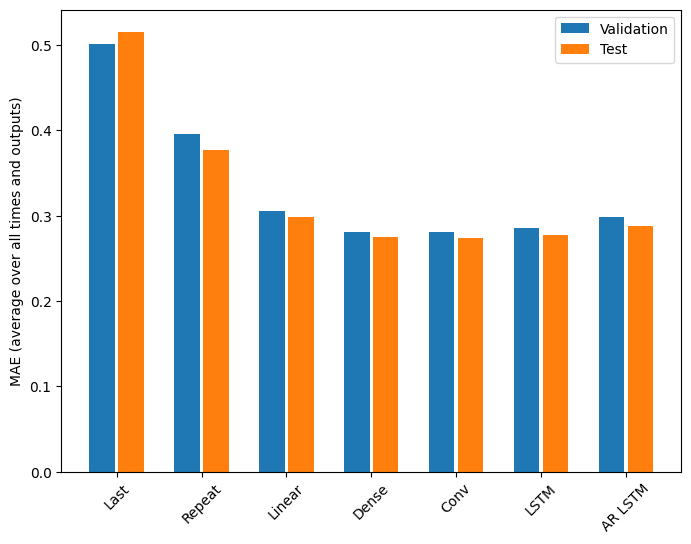
Các chỉ số cho các mô hình nhiều đầu ra trong nửa đầu của hướng dẫn này cho thấy hiệu suất được tính trung bình trên tất cả các tính năng đầu ra. Các hiệu suất này tương tự nhưng cũng được tính trung bình qua các bước thời gian đầu ra.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[1]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2977 Dense : 0.2781 Conv : 0.2796 LSTM : 0.2767 AR LSTM : 0.2901
Lợi ích đạt được khi chuyển từ mô hình dày đặc sang mô hình tích tụ và lặp lại chỉ là một vài phần trăm (nếu có), và mô hình tự phục hồi hoạt động kém hơn rõ ràng. Vì vậy, những cách tiếp cận phức tạp hơn này có thể không có giá trị trong vấn đề này , nhưng không có cách nào để biết nếu không thử và những mô hình này có thể hữu ích cho vấn đề của bạn .
Bước tiếp theo
Hướng dẫn này là phần giới thiệu nhanh về dự báo chuỗi thời gian bằng TensorFlow.
Để tìm hiểu thêm, hãy tham khảo:
- Chương 15 của Học máy thực hành với Scikit-Learn, Keras và TensorFlow , Ấn bản thứ 2.
- Chương 6 của Học sâu với Python .
- Bài 8 trong phần giới thiệu của Udacity về TensorFlow để học sâu , bao gồm cả sổ tay bài tập .
Ngoài ra, hãy nhớ rằng bạn có thể triển khai bất kỳ mô hình chuỗi thời gian cổ điển nào trong TensorFlow — hướng dẫn này chỉ tập trung vào chức năng tích hợp của TensorFlow.
