 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
בבעיית רגרסיה , המטרה היא לחזות את התפוקה של ערך רציף, כמו מחיר או הסתברות. יש להשוות זאת עם בעיית סיווג , שבה המטרה היא לבחור מחלקה מרשימת מחלקות (לדוגמה, כאשר תמונה מכילה תפוח או תפוז, לזהות איזה פרי יש בתמונה).
מדריך זה משתמש במערך הנתונים הקלאסי של Auto MPG ומדגים כיצד לבנות מודלים לחזות את יעילות הדלק של מכוניות של סוף שנות ה-70 ותחילת שנות ה-80. לשם כך, תספק לדגמים תיאור של מכוניות רבות מאותה תקופה. תיאור זה כולל תכונות כמו צילינדרים, תזוזה, כוח סוס ומשקל.
דוגמה זו משתמשת ב-Keras API. (בקר במדריכים ובמדריכים של Keras כדי ללמוד עוד.)
# Use seaborn for pairplot.pip install -q seaborn
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# Make NumPy printouts easier to read.
np.set_printoptions(precision=3, suppress=True)
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
2.8.0-rc1
מערך הנתונים האוטומטי של MPG
מערך הנתונים זמין מ- UCI Machine Learning Repository .
קבל את הנתונים
ראשית הורד וייבא את מערך הנתונים באמצעות פנדות:
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
column_names = ['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(url, names=column_names,
na_values='?', comment='\t',
sep=' ', skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
נקה את הנתונים
מערך הנתונים מכיל כמה ערכים לא ידועים:
dataset.isna().sum()
MPG 0 Cylinders 0 Displacement 0 Horsepower 6 Weight 0 Acceleration 0 Model Year 0 Origin 0 dtype: int64
שחרר את השורות האלה כדי לשמור על המדריך הראשוני הזה פשוט:
dataset = dataset.dropna()
העמודה "Origin" היא קטגורית, לא מספרית. אז השלב הבא הוא קידוד חד-חם של הערכים בעמודה עם pd.get_dummies .
dataset['Origin'] = dataset['Origin'].map({1: 'USA', 2: 'Europe', 3: 'Japan'})
dataset = pd.get_dummies(dataset, columns=['Origin'], prefix='', prefix_sep='')
dataset.tail()
פצל את הנתונים לקבוצות הדרכה ומבחנים
כעת, פצל את מערך הנתונים לסט הדרכה וערכת מבחן. אתה תשתמש בערכת המבחנים בהערכה הסופית של המודלים שלך.
train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)
בדוק את הנתונים
סקור את החלוקה המשותפת של כמה זוגות עמודים ממערך האימונים.
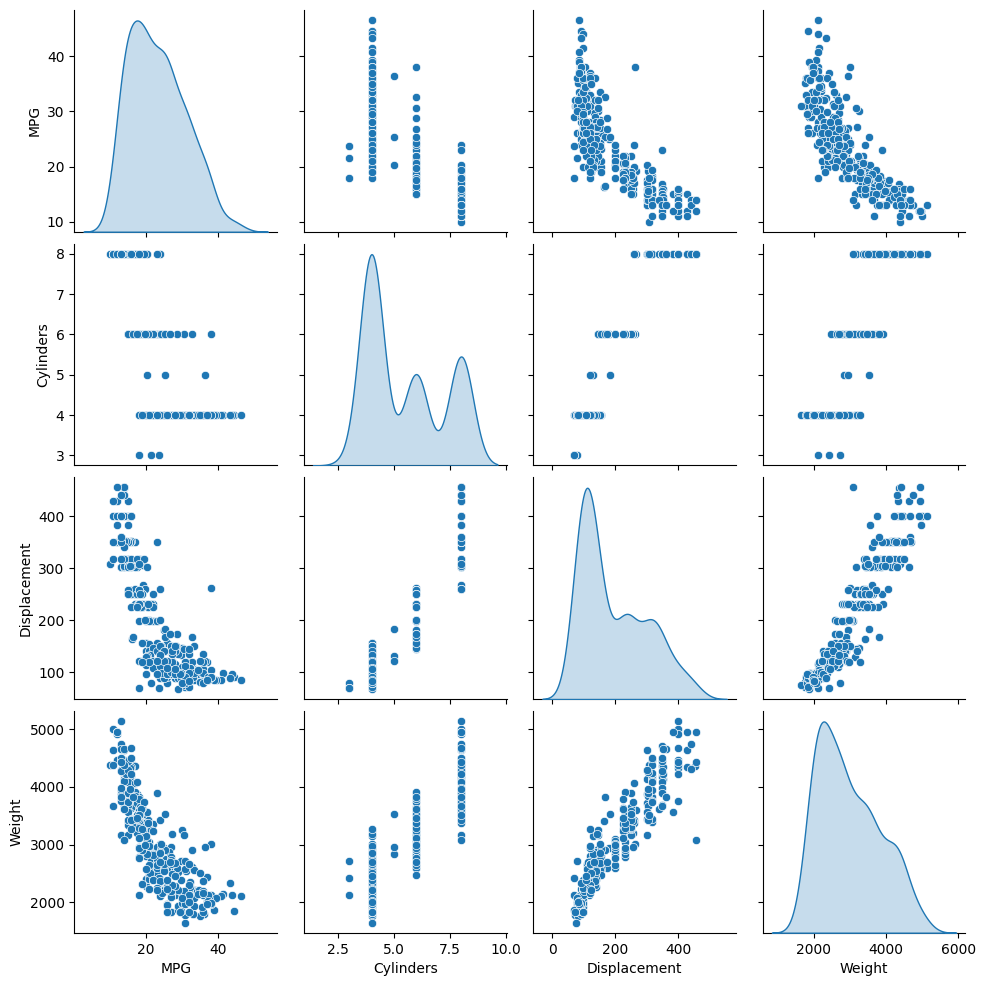
השורה העליונה מציעה שיעילות הדלק (MPG) היא פונקציה של כל שאר הפרמטרים. השורות האחרות מציינות שהן פונקציות זו של זו.
sns.pairplot(train_dataset[['MPG', 'Cylinders', 'Displacement', 'Weight']], diag_kind='kde')
<seaborn.axisgrid.PairGrid at 0x7f6bfdae9850>
בואו נבדוק גם את הסטטיסטיקה הכוללת. שימו לב כיצד כל תכונה מכסה טווח שונה מאוד:
train_dataset.describe().transpose()
פיצול תכונות מהתוויות
הפרד את ערך היעד - ה"תווית" - מהתכונות. תווית זו היא הערך שתאמן את המודל לחזות.
train_features = train_dataset.copy()
test_features = test_dataset.copy()
train_labels = train_features.pop('MPG')
test_labels = test_features.pop('MPG')
נוֹרמָלִיזָצִיָה
בטבלת הסטטיסטיקה קל לראות עד כמה שונים הטווחים של כל תכונה:
train_dataset.describe().transpose()[['mean', 'std']]
זה תרגול טוב לנרמל תכונות המשתמשות בקנה מידה וטווחים שונים.
אחת הסיבות שזה חשוב היא כי התכונות מוכפלות במשקלי הדגם. אז, קנה המידה של התפוקות וקנה המידה של השיפועים מושפעים מקנה המידה של התשומות.
למרות שמודל עשוי להתכנס ללא נורמליזציה של תכונה, נורמליזציה הופכת את האימון ליציב הרבה יותר.
שכבת הנורמליזציה
ה- tf.keras.layers.Normalization היא דרך נקייה ופשוטה להוסיף נורמליזציה של תכונה למודל שלך.
השלב הראשון הוא ליצור את השכבה:
normalizer = tf.keras.layers.Normalization(axis=-1)
לאחר מכן, התאם את המצב של שכבת העיבוד המקדים לנתונים על ידי קריאה ל- Normalization.adapt :
normalizer.adapt(np.array(train_features))
חשב את הממוצע והשונות ואחסן אותם בשכבה:
print(normalizer.mean.numpy())
[[ 5.478 195.318 104.869 2990.252 15.559 75.898 0.178 0.197
0.624]]
כאשר השכבה נקראת, היא מחזירה את נתוני הקלט, כאשר כל תכונה מנורמלת באופן עצמאי:
first = np.array(train_features[:1])
with np.printoptions(precision=2, suppress=True):
print('First example:', first)
print()
print('Normalized:', normalizer(first).numpy())
First example: [[ 4. 90. 75. 2125. 14.5 74. 0. 0. 1. ]] Normalized: [[-0.87 -1.01 -0.79 -1.03 -0.38 -0.52 -0.47 -0.5 0.78]]
רגרסיה לינארית
לפני בניית מודל רשת עצבית עמוקה, התחל עם רגרסיה ליניארית באמצעות משתנה אחד ומספר משתנה.
רגרסיה לינארית עם משתנה אחד
התחל עם רגרסיה ליניארית עם משתנה יחיד כדי לחזות 'MPG' 'Horsepower' .
אימון מודל עם tf.keras מתחיל בדרך כלל בהגדרת ארכיטקטורת המודל. השתמש במודל tf.keras.Sequential , המייצג רצף של שלבים .
ישנם שני שלבים במודל הרגרסיה הלינארית החד-משתני שלך:
- נרמל את תכונות הקלט
'Horsepower'באמצעות שכבת העיבוד המקדיםtf.keras.layers.Normalization. - החל טרנספורמציה ליניארית (\(y = mx+b\)) כדי לייצר פלט אחד באמצעות שכבה ליניארית (
tf.keras.layers.Dense).
ניתן להגדיר את מספר הכניסות באמצעות הארגומנט input_shape , או באופן אוטומטי כאשר המודל מופעל בפעם הראשונה.
ראשית, צור מערך NumPy העשוי מתכונות 'Horsepower' . לאחר מכן, בצע מופע של tf.keras.layers.Normalization את מצבו לנתוני horsepower :
horsepower = np.array(train_features['Horsepower'])
horsepower_normalizer = layers.Normalization(input_shape=[1,], axis=None)
horsepower_normalizer.adapt(horsepower)
בנה את מודל Keras Sequential:
horsepower_model = tf.keras.Sequential([
horsepower_normalizer,
layers.Dense(units=1)
])
horsepower_model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense (Dense) (None, 1) 2
=================================================================
Total params: 5
Trainable params: 2
Non-trainable params: 3
_________________________________________________________________
מודל זה חוזה 'MPG' מ- 'Horsepower' .
הפעל את הדגם הלא מאומן על 10 ערכי 'כוח סוס' הראשונים. הפלט לא יהיה טוב, אבל שימו לב שיש לו את הצורה הצפויה של (10, 1) :
horsepower_model.predict(horsepower[:10])
array([[-1.186],
[-0.67 ],
[ 2.189],
[-1.662],
[-1.504],
[-0.59 ],
[-1.782],
[-1.504],
[-0.392],
[-0.67 ]], dtype=float32)
לאחר בניית המודל, הגדר את הליך ההדרכה באמצעות שיטת Model.compile . הטיעונים החשובים ביותר לקומפילציה הם loss optimizer , מכיוון שאלו מגדירים מה ימוטב ( mean_absolute_error ) וכיצד (באמצעות ה- tf.keras.optimizers.Adam ).
horsepower_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
השתמש ב-Keras Model.fit כדי לבצע את ההדרכה במשך 100 עידנים:
%%time
history = horsepower_model.fit(
train_features['Horsepower'],
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.79 s, sys: 797 ms, total: 5.59 s Wall time: 3.8 s
דמיין את התקדמות האימון של המודל באמצעות הנתונים הסטטיסטיים המאוחסנים באובייקט history :
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_loss(history):
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.ylim([0, 10])
plt.xlabel('Epoch')
plt.ylabel('Error [MPG]')
plt.legend()
plt.grid(True)
plot_loss(history)
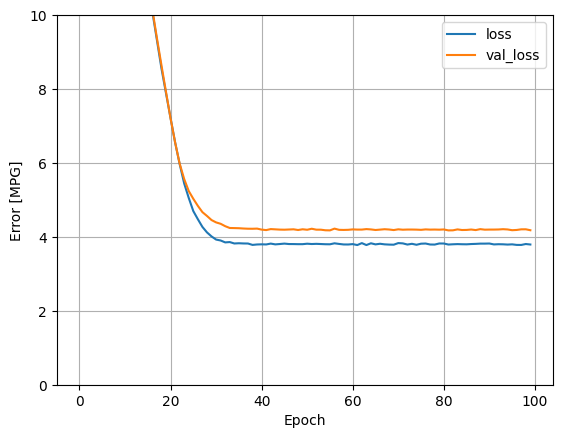
אסוף את התוצאות על ערכת הבדיקה למועד מאוחר יותר:
test_results = {}
test_results['horsepower_model'] = horsepower_model.evaluate(
test_features['Horsepower'],
test_labels, verbose=0)
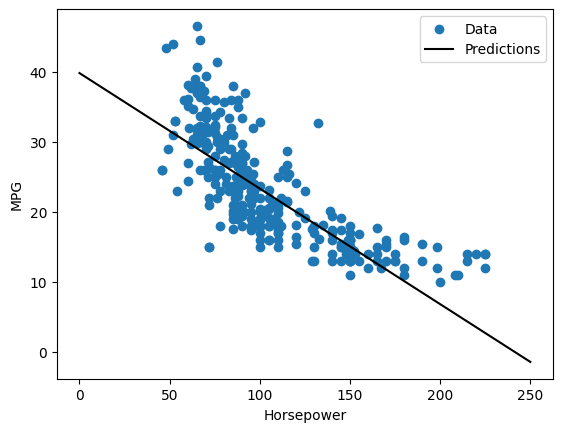
מכיוון שזוהי רגרסיה של משתנה בודד, קל לראות את התחזיות של המודל כפונקציה של הקלט:
x = tf.linspace(0.0, 250, 251)
y = horsepower_model.predict(x)
def plot_horsepower(x, y):
plt.scatter(train_features['Horsepower'], train_labels, label='Data')
plt.plot(x, y, color='k', label='Predictions')
plt.xlabel('Horsepower')
plt.ylabel('MPG')
plt.legend()
plot_horsepower(x, y)
רגרסיה לינארית עם מספר כניסות
אתה יכול להשתמש בהגדרה כמעט זהה כדי לבצע תחזיות המבוססות על מספר כניסות. המודל הזה עדיין עושה את אותו ה- \(y = mx+b\) פרט לכך ש- \(m\) הוא מטריצה ו- \(b\) הוא וקטור.
צור שוב מודל Keras Sequential דו-שלבי כשהשכבה הראשונה היא normalizer ( tf.keras.layers.Normalization(axis=-1) ) שהגדרת קודם לכן והתאמת לכל מערך הנתונים:
linear_model = tf.keras.Sequential([
normalizer,
layers.Dense(units=1)
])
כאשר אתה קורא Model.predict על אצווה של תשומות, הוא מייצר units=1 פלטים עבור כל דוגמה:
linear_model.predict(train_features[:10])
array([[ 0.441],
[ 1.522],
[ 0.188],
[ 1.169],
[ 0.058],
[ 0.965],
[ 0.034],
[-0.674],
[ 0.437],
[-0.37 ]], dtype=float32)
כאשר אתה קורא למודל, מטריצות המשקל שלו ייבנו - בדוק kernel (ה- \(m\) ב- \(y=mx+b\)) יש צורה של (9, 1) :
linear_model.layers[1].kernel
<tf.Variable 'dense_1/kernel:0' shape=(9, 1) dtype=float32, numpy=
array([[-0.702],
[ 0.307],
[ 0.114],
[ 0.233],
[ 0.244],
[ 0.322],
[-0.725],
[-0.151],
[ 0.407]], dtype=float32)>
הגדר את הדגם עם Keras Model.compile עם Model.fit למשך 100 עידנים:
linear_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
%%time
history = linear_model.fit(
train_features,
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.89 s, sys: 740 ms, total: 5.63 s Wall time: 3.75 s
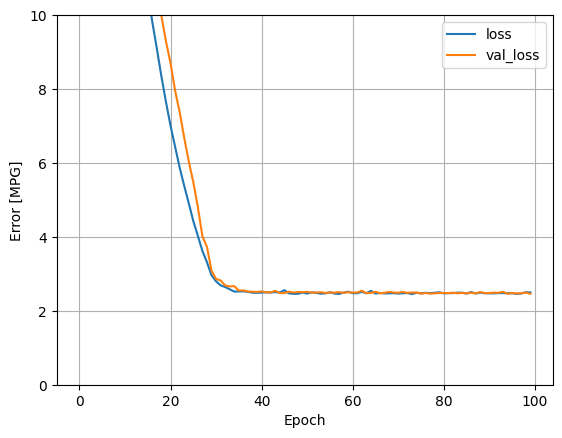
שימוש בכל התשומות במודל הרגרסיה הזה משיג שגיאת אימון ותיקוף נמוכה בהרבה מאשר במודל horsepower_model , שהיה לו קלט אחד:
plot_loss(history)
אסוף את התוצאות על ערכת הבדיקה למועד מאוחר יותר:
test_results['linear_model'] = linear_model.evaluate(
test_features, test_labels, verbose=0)
רגרסיה עם רשת עצבית עמוקה (DNN)
בסעיף הקודם, יישמת שני מודלים ליניאריים עבור כניסות בודדות ומרובות.
כאן תוכלו ליישם דגמי DNN עם קלט יחיד וכניסה מרובה.
הקוד בעצם זהה למעט שהמודל מורחב כך שיכלול כמה שכבות לא ליניאריות "חבויות". פירוש השם "נסתר" כאן פשוט אינו מחובר ישירות לכניסות או ליציאות.
מודלים אלה יכילו עוד כמה שכבות מהמודל הליניארי:
- שכבת הנורמליזציה, כמו קודם (עם
horsepower_normalizerעבור מודל בעל קלט בודדnormalizerעבור מודל מרובה כניסות). - שתי שכבות נסתרות, לא ליניאריות,
Denseעם אי-לינאריות של פונקציית ההפעלה ReLU (relu). - שכבת פלט יחיד ליניארית
Dense.
שני המודלים ישתמשו באותו הליך הדרכה ולכן שיטת build_and_compile_model compile .
def build_and_compile_model(norm):
model = keras.Sequential([
norm,
layers.Dense(64, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
model.compile(loss='mean_absolute_error',
optimizer=tf.keras.optimizers.Adam(0.001))
return model
רגרסיה באמצעות DNN וקלט בודד
צור מודל DNN עם רק 'Horsepower' כקלט ו- horsepower_normalizer (הוגדר קודם לכן) כשכבת הנורמליזציה:
dnn_horsepower_model = build_and_compile_model(horsepower_normalizer)
לדגם הזה יש לא מעט פרמטרים ניתנים לאימון מאשר לדגמים הליניאריים:
dnn_horsepower_model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense_2 (Dense) (None, 64) 128
dense_3 (Dense) (None, 64) 4160
dense_4 (Dense) (None, 1) 65
=================================================================
Total params: 4,356
Trainable params: 4,353
Non-trainable params: 3
_________________________________________________________________
אימון הדוגמנית עם Keras Model.fit :
%%time
history = dnn_horsepower_model.fit(
train_features['Horsepower'],
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.07 s, sys: 691 ms, total: 5.76 s Wall time: 3.92 s
מודל זה מצליח מעט יותר מאשר מודל horsepower_model עם קלט יחיד ליניארי:
plot_loss(history)
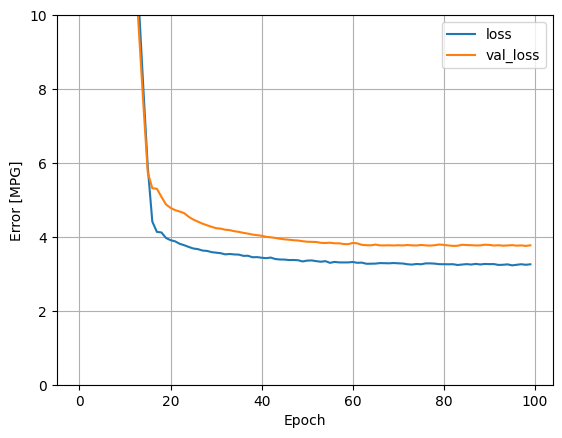
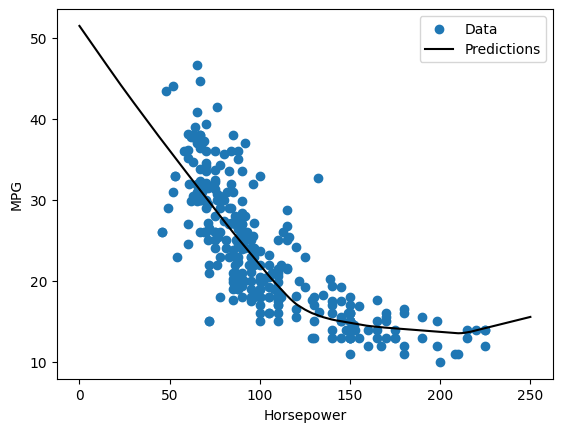
אם אתה מתווה את התחזיות כפונקציה של 'Horsepower' , אתה צריך לשים לב כיצד המודל הזה מנצל את חוסר הלינאריות שמספקות השכבות הנסתרות:
x = tf.linspace(0.0, 250, 251)
y = dnn_horsepower_model.predict(x)
plot_horsepower(x, y)
אסוף את התוצאות על ערכת הבדיקה למועד מאוחר יותר:
test_results['dnn_horsepower_model'] = dnn_horsepower_model.evaluate(
test_features['Horsepower'], test_labels,
verbose=0)
רגרסיה באמצעות DNN וכניסות מרובות
חזור על התהליך הקודם תוך שימוש בכל הכניסות. ביצועי המודל משתפרים מעט במערך האימות.
dnn_model = build_and_compile_model(normalizer)
dnn_model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization (Normalizatio (None, 9) 19
n)
dense_5 (Dense) (None, 64) 640
dense_6 (Dense) (None, 64) 4160
dense_7 (Dense) (None, 1) 65
=================================================================
Total params: 4,884
Trainable params: 4,865
Non-trainable params: 19
_________________________________________________________________
%%time
history = dnn_model.fit(
train_features,
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.08 s, sys: 725 ms, total: 5.8 s Wall time: 3.94 s
plot_loss(history)
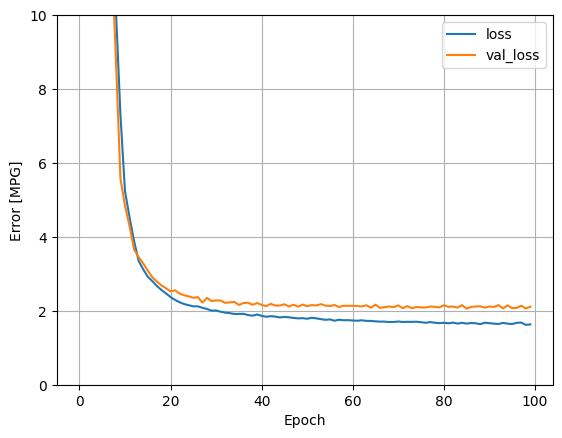
אסוף את התוצאות על ערכת הבדיקה:
test_results['dnn_model'] = dnn_model.evaluate(test_features, test_labels, verbose=0)
ביצועים
מכיוון שכל הדגמים עברו הכשרה, אתה יכול לסקור את ביצועי ערכת המבחן שלהם:
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
תוצאות אלו תואמות את שגיאת האימות שנצפתה במהלך האימון.
לעשות תחזיות
כעת תוכל לבצע תחזיות עם ה- dnn_model הבדיקה באמצעות Keras Model.predict ולסקור את ההפסד:
test_predictions = dnn_model.predict(test_features).flatten()
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
lims = [0, 50]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)

נראה שהמודל מנבא בצורה סבירה.
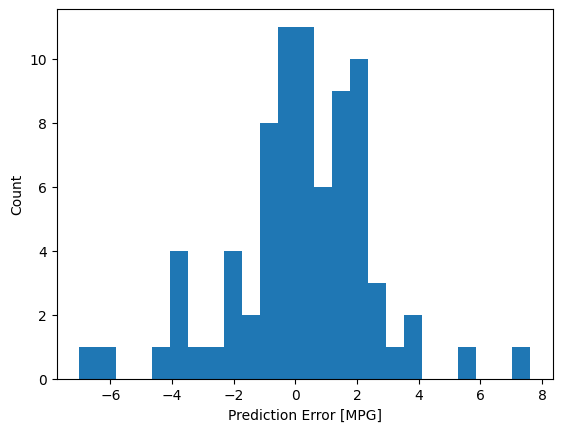
כעת, בדוק את התפלגות השגיאות:
error = test_predictions - test_labels
plt.hist(error, bins=25)
plt.xlabel('Prediction Error [MPG]')
_ = plt.ylabel('Count')
אם אתה מרוצה מהדגם, שמור אותו לשימוש מאוחר יותר עם Model.save :
dnn_model.save('dnn_model')
2022-01-26 07:26:13.372245: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: dnn_model/assets
אם אתה טוען מחדש את הדגם, הוא נותן פלט זהה:
reloaded = tf.keras.models.load_model('dnn_model')
test_results['reloaded'] = reloaded.evaluate(
test_features, test_labels, verbose=0)
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
סיכום
מחברת זו הציג כמה טכניקות לטיפול בבעיית רגרסיה. הנה כמה טיפים נוספים שעשויים לעזור:
- שגיאה ממוצעת בריבוע (MSE) (
tf.losses.MeanSquaredError) ושגיאה ממוצעת (MAE) (tf.losses.MeanAbsoluteError) הן פונקציות אובדן נפוצות המשמשות לבעיות רגרסיה. MAE פחות רגיש לחריגים. פונקציות אובדן שונות משמשות לבעיות סיווג. - באופן דומה, מדדי הערכה המשמשים לרגרסיה שונים מסיווג.
- כאשר למאפייני נתוני קלט מספריים יש ערכים עם טווחים שונים, יש לשנות את קנה המידה של כל תכונה באופן עצמאי לאותו טווח.
- התאמת יתר היא בעיה נפוצה עבור דגמי DNN, אם כי זו לא הייתה בעיה עבור הדרכה זו. בקר במדריך כושר יתר וחוסר כושר לעזרה נוספת בנושא זה.
# MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
