 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запустить в Google Colab Запустить в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
В задаче регрессии цель состоит в том, чтобы предсказать вывод непрерывного значения, такого как цена или вероятность. Сравните это с проблемой классификации , где цель состоит в том, чтобы выбрать класс из списка классов (например, если на картинке изображено яблоко или апельсин, распознать, какой фрукт изображен на картинке).
В этом руководстве используется классический набор данных Auto MPG и демонстрируется создание моделей для прогнозирования топливной экономичности автомобилей конца 1970-х и начала 1980-х годов. Для этого вы снабдите модели описанием многих автомобилей того времени. Это описание включает такие атрибуты, как цилиндры, рабочий объем, мощность и вес.
В этом примере используется Keras API. (Посетите учебные пособия и руководства Keras, чтобы узнать больше.)
# Use seaborn for pairplot.pip install -q seaborn
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# Make NumPy printouts easier to read.
np.set_printoptions(precision=3, suppress=True)
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
2.8.0-rc1
Набор данных Auto MPG
Набор данных доступен в репозитории машинного обучения UCI .
Получить данные
Сначала загрузите и импортируйте набор данных с помощью pandas:
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
column_names = ['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(url, names=column_names,
na_values='?', comment='\t',
sep=' ', skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
Очистить данные
Набор данных содержит несколько неизвестных значений:
dataset.isna().sum()
MPG 0 Cylinders 0 Displacement 0 Horsepower 6 Weight 0 Acceleration 0 Model Year 0 Origin 0 dtype: int64
Удалите эти строки, чтобы сделать этот начальный учебник простым:
dataset = dataset.dropna()
Столбец "Origin" является категориальным, а не числовым. Итак, следующим шагом будет горячее кодирование значений в столбце с помощью pd.get_dummies .
dataset['Origin'] = dataset['Origin'].map({1: 'USA', 2: 'Europe', 3: 'Japan'})
dataset = pd.get_dummies(dataset, columns=['Origin'], prefix='', prefix_sep='')
dataset.tail()
Разделите данные на обучающие и тестовые наборы
Теперь разделите набор данных на обучающий набор и тестовый набор. Вы будете использовать тестовый набор для окончательной оценки ваших моделей.
train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)
Проверить данные
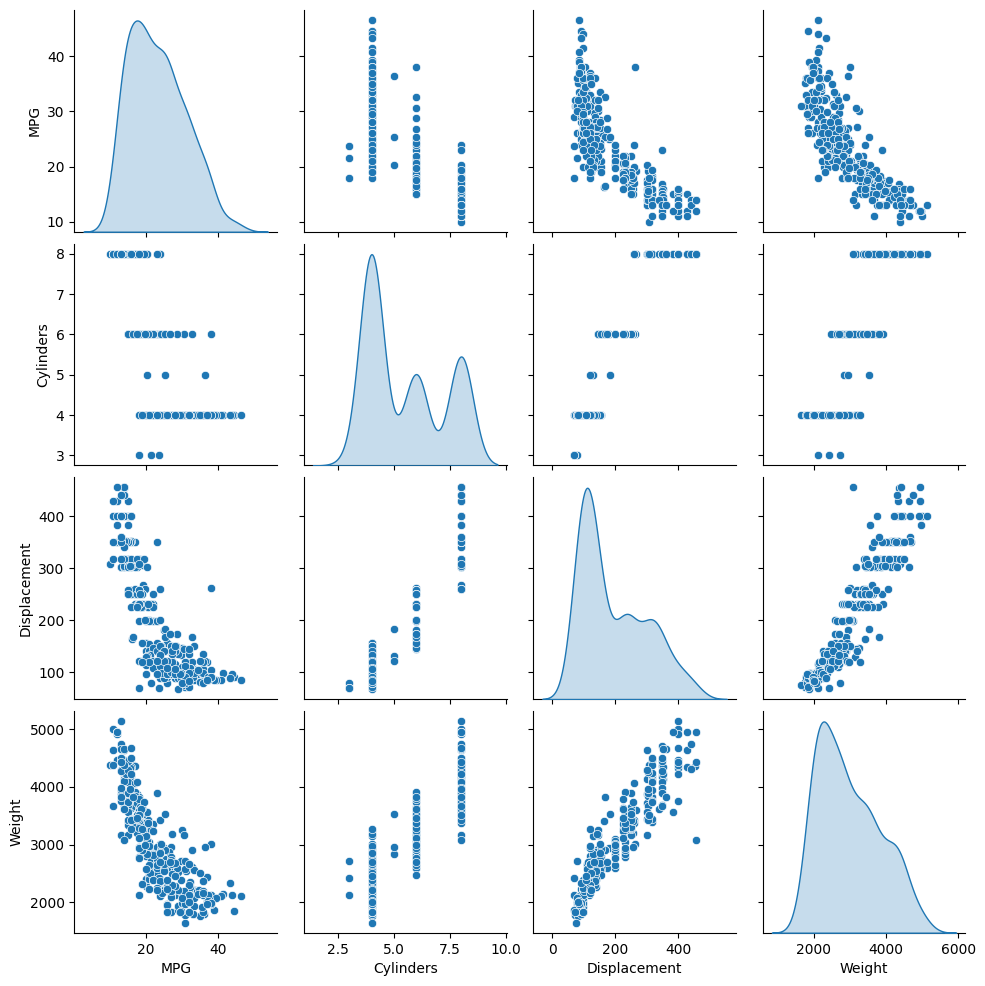
Просмотрите совместное распределение нескольких пар столбцов из обучающей выборки.
Верхний ряд предполагает, что эффективность использования топлива (MPG) является функцией всех других параметров. В других строках указано, что они являются функциями друг друга.
sns.pairplot(train_dataset[['MPG', 'Cylinders', 'Displacement', 'Weight']], diag_kind='kde')
<seaborn.axisgrid.PairGrid at 0x7f6bfdae9850>
Давайте также проверим общую статистику. Обратите внимание, что каждая функция охватывает очень разные диапазоны:
train_dataset.describe().transpose()
Отделить функции от меток
Отделите целевое значение — «метку» — от признаков. Эта метка является значением, которое вы будете обучать модели прогнозировать.
train_features = train_dataset.copy()
test_features = test_dataset.copy()
train_labels = train_features.pop('MPG')
test_labels = test_features.pop('MPG')
Нормализация
В таблице статистики легко увидеть, насколько различны диапазоны каждого признака:
train_dataset.describe().transpose()[['mean', 'std']]
Хорошей практикой является нормализация функций, использующих разные масштабы и диапазоны.
Одна из причин, по которой это важно, заключается в том, что функции умножаются на веса модели. Таким образом, масштаб выходных данных и масштаб градиентов зависят от масштаба входных данных.
Хотя модель может сходиться без нормализации признаков, нормализация делает обучение более стабильным.
Слой нормализации
tf.keras.layers.Normalization — это чистый и простой способ добавить нормализацию признаков в вашу модель.
Первым шагом является создание слоя:
normalizer = tf.keras.layers.Normalization(axis=-1)
Затем подгоните состояние слоя предварительной обработки к данным, вызвав Normalization.adapt :
normalizer.adapt(np.array(train_features))
Вычислите среднее значение и дисперсию и сохраните их в слое:
print(normalizer.mean.numpy())
[[ 5.478 195.318 104.869 2990.252 15.559 75.898 0.178 0.197
0.624]]
Когда слой вызывается, он возвращает входные данные, причем каждая функция нормализована независимо:
first = np.array(train_features[:1])
with np.printoptions(precision=2, suppress=True):
print('First example:', first)
print()
print('Normalized:', normalizer(first).numpy())
First example: [[ 4. 90. 75. 2125. 14.5 74. 0. 0. 1. ]] Normalized: [[-0.87 -1.01 -0.79 -1.03 -0.38 -0.52 -0.47 -0.5 0.78]]
Линейная регрессия
Прежде чем строить модель глубокой нейронной сети, начните с линейной регрессии с использованием одной и нескольких переменных.
Линейная регрессия с одной переменной
Начните с линейной регрессии с одной переменной, чтобы предсказать 'MPG' по 'Horsepower' .
Обучение модели с помощью tf.keras обычно начинается с определения архитектуры модели. Используйте модель tf.keras.Sequential , которая представляет собой последовательность шагов .
В вашей модели линейной регрессии с одной переменной есть два шага:
- Нормализуйте входные функции
'Horsepower'используя слой предварительной обработкиtf.keras.layers.Normalization. - Примените линейное преобразование (\(y = mx+b\)) для создания 1 вывода с использованием линейного слоя (
tf.keras.layers.Dense).
Количество входных данных может быть установлено либо аргументом input_shape , либо автоматически при первом запуске модели.
Во-первых, создайте массив NumPy, состоящий из функций 'Horsepower' . Затем создайте экземпляр tf.keras.layers.Normalization и сопоставьте его состояние с данными о horsepower :
horsepower = np.array(train_features['Horsepower'])
horsepower_normalizer = layers.Normalization(input_shape=[1,], axis=None)
horsepower_normalizer.adapt(horsepower)
Постройте модель Keras Sequential:
horsepower_model = tf.keras.Sequential([
horsepower_normalizer,
layers.Dense(units=1)
])
horsepower_model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense (Dense) (None, 1) 2
=================================================================
Total params: 5
Trainable params: 2
Non-trainable params: 3
_________________________________________________________________
Эта модель будет предсказывать 'MPG' по 'Horsepower' .
Запустите необученную модель на первых 10 значениях «лошадиных сил». Результат не будет хорошим, но обратите внимание, что он имеет ожидаемую форму (10, 1) :
horsepower_model.predict(horsepower[:10])
array([[-1.186],
[-0.67 ],
[ 2.189],
[-1.662],
[-1.504],
[-0.59 ],
[-1.782],
[-1.504],
[-0.392],
[-0.67 ]], dtype=float32)
После построения модели настройте процедуру обучения, используя метод Model.compile . Наиболее важными аргументами для компиляции являются loss и optimizer , поскольку они определяют, что будет оптимизировано ( mean_absolute_error ) и как (используя tf.keras.optimizers.Adam ).
horsepower_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
Используйте Model.fit для выполнения обучения на 100 эпох:
%%time
history = horsepower_model.fit(
train_features['Horsepower'],
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.79 s, sys: 797 ms, total: 5.59 s Wall time: 3.8 s
Визуализируйте ход обучения модели, используя статистику, хранящуюся в объекте history :
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_loss(history):
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.ylim([0, 10])
plt.xlabel('Epoch')
plt.ylabel('Error [MPG]')
plt.legend()
plt.grid(True)
plot_loss(history)
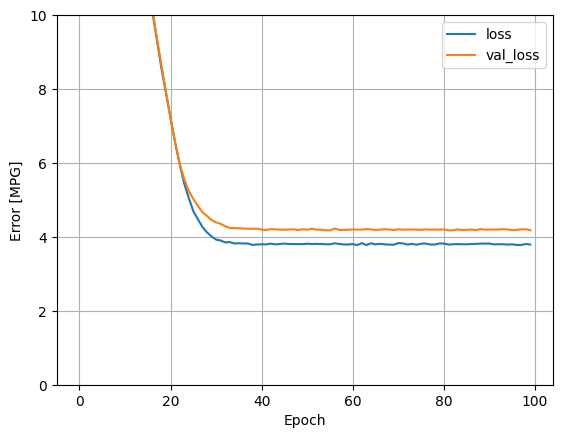
Соберите результаты на тестовом наборе на потом:
test_results = {}
test_results['horsepower_model'] = horsepower_model.evaluate(
test_features['Horsepower'],
test_labels, verbose=0)
Поскольку это регрессия с одной переменной, прогнозы модели легко просмотреть как функцию входных данных:
x = tf.linspace(0.0, 250, 251)
y = horsepower_model.predict(x)
def plot_horsepower(x, y):
plt.scatter(train_features['Horsepower'], train_labels, label='Data')
plt.plot(x, y, color='k', label='Predictions')
plt.xlabel('Horsepower')
plt.ylabel('MPG')
plt.legend()
plot_horsepower(x, y)
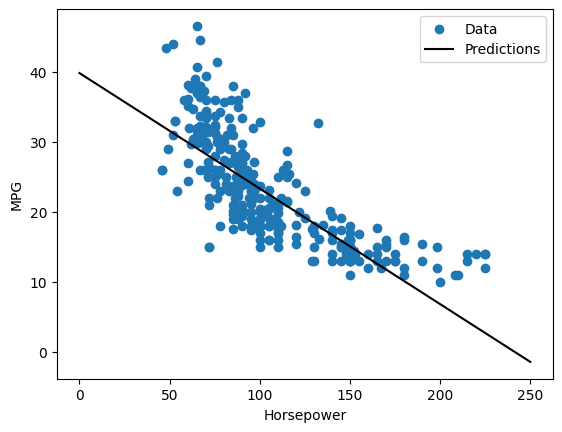
Линейная регрессия с несколькими входами
Вы можете использовать почти идентичную настройку, чтобы делать прогнозы на основе нескольких входных данных. Эта модель по-прежнему делает то же самое \(y = mx+b\) , за исключением того, что \(m\) — это матрица, а \(b\) — это вектор.
Снова создайте двухэтапную модель Keras Sequential с первым слоем, являющимся normalizer ( tf.keras.layers.Normalization(axis=-1) ), который вы определили ранее и адаптировали ко всему набору данных:
linear_model = tf.keras.Sequential([
normalizer,
layers.Dense(units=1)
])
Когда вы вызываете Model.predict для пакета входных данных, он выдает units=1 для каждого примера:
linear_model.predict(train_features[:10])
array([[ 0.441],
[ 1.522],
[ 0.188],
[ 1.169],
[ 0.058],
[ 0.965],
[ 0.034],
[-0.674],
[ 0.437],
[-0.37 ]], dtype=float32)
Когда вы вызываете модель, ее весовые матрицы будут построены — убедитесь, что веса kernel ( \(m\) в \(y=mx+b\)) имеют форму (9, 1) :
linear_model.layers[1].kernel
<tf.Variable 'dense_1/kernel:0' shape=(9, 1) dtype=float32, numpy=
array([[-0.702],
[ 0.307],
[ 0.114],
[ 0.233],
[ 0.244],
[ 0.322],
[-0.725],
[-0.151],
[ 0.407]], dtype=float32)>
Настройте модель с помощью Model.compile и обучите с помощью Model.fit в течение 100 эпох:
linear_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
%%time
history = linear_model.fit(
train_features,
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.89 s, sys: 740 ms, total: 5.63 s Wall time: 3.75 s
Использование всех входных данных в этой регрессионной модели обеспечивает гораздо меньшую ошибку обучения и проверки, чем horsepower_model , у которой был один вход:
plot_loss(history)
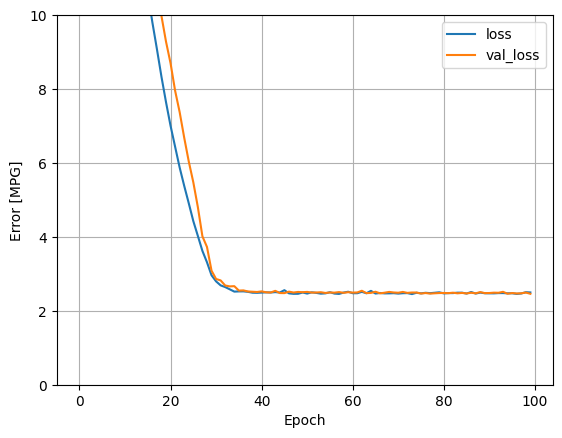
Соберите результаты на тестовом наборе на потом:
test_results['linear_model'] = linear_model.evaluate(
test_features, test_labels, verbose=0)
Регрессия с глубокой нейронной сетью (DNN)
В предыдущем разделе вы реализовали две линейные модели для одного и нескольких входов.
Здесь вы будете реализовывать модели DNN с одним входом и несколькими входами.
Код в основном такой же, за исключением того, что модель расширена за счет включения некоторых «скрытых» нелинейных слоев. Название «скрытый» здесь просто означает, что он не подключен напрямую к входам или выходам.
Эти модели будут содержать на несколько слоев больше, чем линейная модель:
- Слой нормализации, как и раньше (с
horsepower_normalizerдля модели с одним входом иnormalizerдля модели с несколькими входами). - Два скрытых, нелинейных,
Denseслоя с нелинейностью функции активации ReLU (relu). - Линейный
Denseслой с одним выходом.
Обе модели будут использовать одну и ту же процедуру обучения, поэтому метод compile включен в функцию build_and_compile_model ниже.
def build_and_compile_model(norm):
model = keras.Sequential([
norm,
layers.Dense(64, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
model.compile(loss='mean_absolute_error',
optimizer=tf.keras.optimizers.Adam(0.001))
return model
Регрессия с использованием DNN и одного входа
Создайте модель DNN только с 'Horsepower' в качестве входных данных и horsepower_normalizer (определенным ранее) в качестве слоя нормализации:
dnn_horsepower_model = build_and_compile_model(horsepower_normalizer)
У этой модели гораздо больше обучаемых параметров, чем у линейных моделей:
dnn_horsepower_model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense_2 (Dense) (None, 64) 128
dense_3 (Dense) (None, 64) 4160
dense_4 (Dense) (None, 1) 65
=================================================================
Total params: 4,356
Trainable params: 4,353
Non-trainable params: 3
_________________________________________________________________
Обучите модель с помощью Model.fit :
%%time
history = dnn_horsepower_model.fit(
train_features['Horsepower'],
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.07 s, sys: 691 ms, total: 5.76 s Wall time: 3.92 s
Эта модель работает немного лучше, чем линейная модель horsepower_model с одним входом:
plot_loss(history)
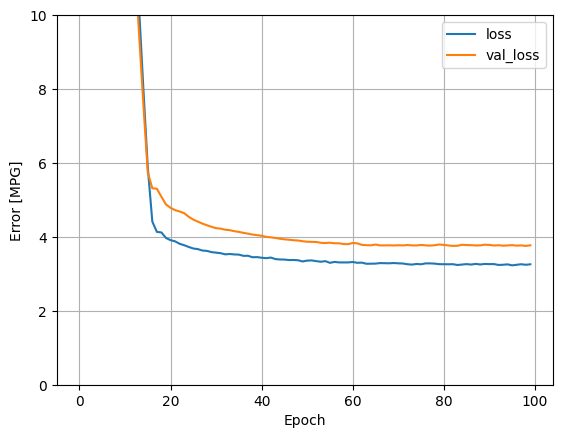
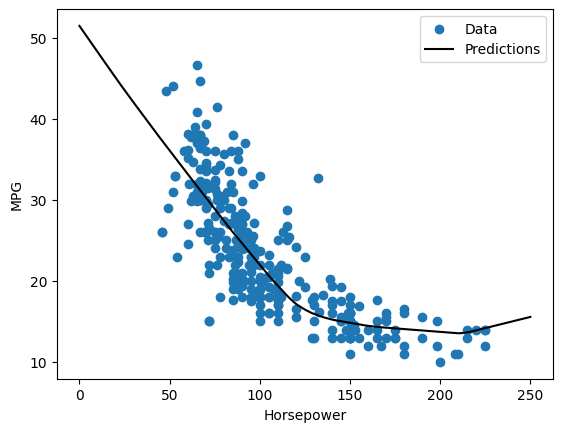
Если вы построите прогнозы как функцию 'Horsepower' , вы должны заметить, как эта модель использует преимущества нелинейности, обеспечиваемой скрытыми слоями:
x = tf.linspace(0.0, 250, 251)
y = dnn_horsepower_model.predict(x)
plot_horsepower(x, y)
Соберите результаты на тестовом наборе на потом:
test_results['dnn_horsepower_model'] = dnn_horsepower_model.evaluate(
test_features['Horsepower'], test_labels,
verbose=0)
Регрессия с использованием DNN и нескольких входных данных
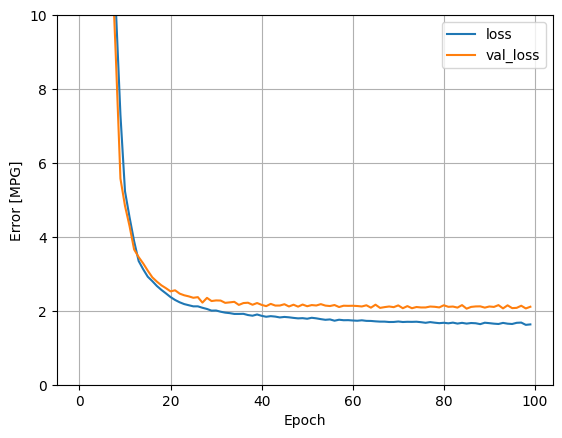
Повторите предыдущий процесс, используя все входы. Производительность модели немного улучшается по сравнению с проверочным набором данных.
dnn_model = build_and_compile_model(normalizer)
dnn_model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization (Normalizatio (None, 9) 19
n)
dense_5 (Dense) (None, 64) 640
dense_6 (Dense) (None, 64) 4160
dense_7 (Dense) (None, 1) 65
=================================================================
Total params: 4,884
Trainable params: 4,865
Non-trainable params: 19
_________________________________________________________________
%%time
history = dnn_model.fit(
train_features,
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.08 s, sys: 725 ms, total: 5.8 s Wall time: 3.94 s
plot_loss(history)
Соберите результаты на тестовом наборе:
test_results['dnn_model'] = dnn_model.evaluate(test_features, test_labels, verbose=0)
Представление
Поскольку все модели были обучены, вы можете просмотреть их производительность тестового набора:
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
Эти результаты соответствуют ошибке проверки, наблюдаемой во время обучения.
Делать предсказания
Теперь вы можете делать прогнозы с помощью dnn_model в тестовом наборе с помощью Model.predict и просматривать потери:
test_predictions = dnn_model.predict(test_features).flatten()
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
lims = [0, 50]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)

Похоже, что модель предсказывает достаточно хорошо.
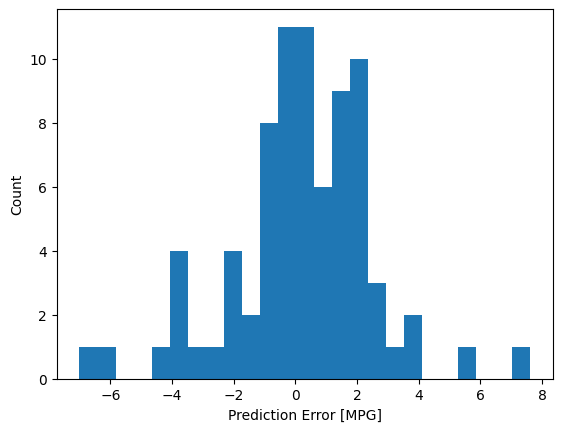
Теперь проверьте распределение ошибок:
error = test_predictions - test_labels
plt.hist(error, bins=25)
plt.xlabel('Prediction Error [MPG]')
_ = plt.ylabel('Count')
Если вы довольны моделью, сохраните ее для последующего использования с помощью Model.save :
dnn_model.save('dnn_model')
2022-01-26 07:26:13.372245: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: dnn_model/assets
Если вы перезагрузите модель, она даст идентичный результат:
reloaded = tf.keras.models.load_model('dnn_model')
test_results['reloaded'] = reloaded.evaluate(
test_features, test_labels, verbose=0)
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
Вывод
В этой записной книжке представлено несколько методов решения проблемы регрессии. Вот еще несколько советов, которые могут помочь:
- Среднеквадратическая ошибка (MSE) (
tf.losses.MeanSquaredError) и средняя абсолютная ошибка (MAE) (tf.losses.MeanAbsoluteError) являются распространенными функциями потерь, используемыми для задач регрессии. MAE менее чувствителен к выбросам. Различные функции потерь используются для задач классификации. - Точно так же показатели оценки, используемые для регрессии, отличаются от классификации.
- Когда функции числовых входных данных имеют значения в разных диапазонах, каждая функция должна масштабироваться независимо до одного и того же диапазона.
- Переобучение — обычная проблема для моделей DNN, хотя в этом руководстве это не было проблемой. Посетите учебник Overfit and underfit для получения дополнительной помощи.
# MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
