 ดูบน TensorFlow.org ดูบน TensorFlow.org |  ทำงานใน Google Colab ทำงานใน Google Colab |  ดูแหล่งที่มาบน GitHub ดูแหล่งที่มาบน GitHub |  ดาวน์โหลดโน๊ตบุ๊ค ดาวน์โหลดโน๊ตบุ๊ค |
ในปัญหา การถดถอย จุดมุ่งหมายคือการทำนายผลลัพธ์ของค่าที่ต่อเนื่องกัน เช่น ราคาหรือความน่าจะเป็น เปรียบเทียบสิ่งนี้กับปัญหาการ จำแนกประเภท โดยมีเป้าหมายคือการเลือกชั้นเรียนจากรายการชั้นเรียน (เช่น ที่รูปภาพประกอบด้วยแอปเปิ้ลหรือส้ม โดยรู้ว่าผลไม้ใดอยู่ในภาพ)
บทช่วยสอนนี้ใช้ชุดข้อมูล Auto MPG แบบคลาสสิกและสาธิตวิธีสร้างแบบจำลองเพื่อคาดการณ์ประสิทธิภาพการใช้เชื้อเพลิงของรถยนต์ช่วงปลายทศวรรษ 1970 และต้นทศวรรษ 1980 ในการทำเช่นนี้ คุณจะต้องให้รายละเอียดของรถยนต์หลายรุ่นในช่วงเวลานั้น คำอธิบายนี้รวมถึงคุณลักษณะต่างๆ เช่น กระบอกสูบ การกระจัด แรงม้า และน้ำหนัก
ตัวอย่างนี้ใช้ Keras API (ไปที่ บทแนะนำ และ คำแนะนำ ของ Keras เพื่อเรียนรู้เพิ่มเติม)
# Use seaborn for pairplot.pip install -q seaborn
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# Make NumPy printouts easier to read.
np.set_printoptions(precision=3, suppress=True)
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
2.8.0-rc1
ชุดข้อมูล MPG อัตโนมัติ
ชุดข้อมูลมีอยู่ใน UCI Machine Learning Repository
รับข้อมูล
ขั้นแรกให้ดาวน์โหลดและนำเข้าชุดข้อมูลโดยใช้แพนด้า:
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
column_names = ['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(url, names=column_names,
na_values='?', comment='\t',
sep=' ', skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
ทำความสะอาดข้อมูล
ชุดข้อมูลมีค่าที่ไม่รู้จักสองสามค่า:
dataset.isna().sum()
MPG 0 Cylinders 0 Displacement 0 Horsepower 6 Weight 0 Acceleration 0 Model Year 0 Origin 0 dtype: int64
วางแถวเหล่านั้นเพื่อให้บทแนะนำเบื้องต้นนี้เรียบง่าย:
dataset = dataset.dropna()
คอลัมน์ "Origin" เป็นหมวดหมู่ ไม่ใช่ตัวเลข ดังนั้นขั้นตอนต่อไปคือการเข้ารหัสค่าในคอลัมน์ด้วย pd.get_dummies
dataset['Origin'] = dataset['Origin'].map({1: 'USA', 2: 'Europe', 3: 'Japan'})
dataset = pd.get_dummies(dataset, columns=['Origin'], prefix='', prefix_sep='')
dataset.tail()
แบ่งข้อมูลออกเป็นชุดฝึกและชุดทดสอบ
ตอนนี้ แบ่งชุดข้อมูลออกเป็นชุดการฝึกและชุดทดสอบ คุณจะใช้ชุดทดสอบในการประเมินขั้นสุดท้ายของแบบจำลองของคุณ
train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)
ตรวจสอบข้อมูล
ตรวจสอบการกระจายร่วมของเสาสองสามคู่จากชุดการฝึก
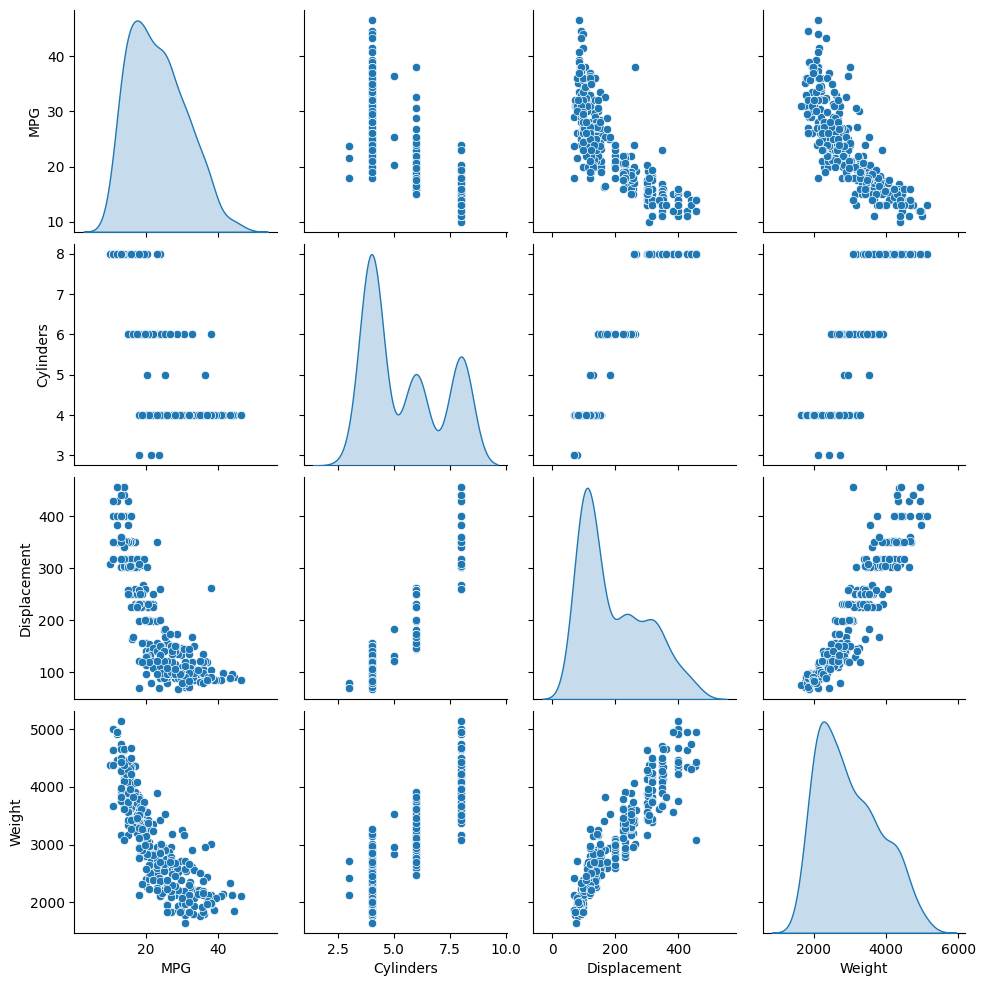
แถวบนสุดแสดงให้เห็นว่าประสิทธิภาพการใช้เชื้อเพลิง (MPG) เป็นฟังก์ชันของพารามิเตอร์อื่นๆ ทั้งหมด แถวอื่น ๆ ระบุว่าเป็นหน้าที่ของกันและกัน
sns.pairplot(train_dataset[['MPG', 'Cylinders', 'Displacement', 'Weight']], diag_kind='kde')
<seaborn.axisgrid.PairGrid at 0x7f6bfdae9850>
ลองตรวจสอบสถิติโดยรวมด้วย โปรดทราบว่าคุณลักษณะแต่ละอย่างครอบคลุมช่วงที่แตกต่างกันมาก:
train_dataset.describe().transpose()
แยกคุณสมบัติออกจากป้ายกำกับ
แยกค่าเป้าหมาย—"ป้ายกำกับ"—ออกจากคุณสมบัติ ป้ายกำกับนี้เป็นค่าที่คุณจะฝึกให้โมเดลคาดการณ์
train_features = train_dataset.copy()
test_features = test_dataset.copy()
train_labels = train_features.pop('MPG')
test_labels = test_features.pop('MPG')
การทำให้เป็นมาตรฐาน
ในตารางสถิติ จะเห็นว่าช่วงของแต่ละฟีเจอร์แตกต่างกันอย่างไร:
train_dataset.describe().transpose()[['mean', 'std']]
แนวทางปฏิบัติที่ดีในการทำให้คุณลักษณะปกติที่ใช้มาตราส่วนและช่วงต่างๆ ต่างกัน ถือเป็นแนวทางปฏิบัติที่ดี
เหตุผลหนึ่งที่สำคัญคือเนื่องจากคุณลักษณะต่างๆ คูณด้วยน้ำหนักของรุ่น ดังนั้น ขนาดของเอาต์พุตและสเกลของการไล่ระดับสีจะได้รับผลกระทบจากสเกลของอินพุต
แม้ว่าแบบจำลอง อาจ มาบรรจบกันโดยไม่มีการทำให้เป็นมาตรฐานของคุณลักษณะ แต่การทำให้เป็นมาตรฐานทำให้การฝึกมีเสถียรภาพมากขึ้น
ชั้น Normalization
tf.keras.layers.Normalization เป็นวิธีที่ง่ายและสะอาดในการเพิ่มการทำให้เป็นมาตรฐานของคุณลักษณะในแบบจำลองของคุณ
ขั้นตอนแรกคือการสร้างเลเยอร์:
normalizer = tf.keras.layers.Normalization(axis=-1)
จากนั้น ปรับสถานะของเลเยอร์การประมวลผลล่วงหน้ากับข้อมูลโดยเรียก Normalization.adapt :
normalizer.adapt(np.array(train_features))
คำนวณค่าเฉลี่ยและความแปรปรวน และเก็บไว้ในเลเยอร์:
print(normalizer.mean.numpy())
[[ 5.478 195.318 104.869 2990.252 15.559 75.898 0.178 0.197
0.624]]
เมื่อเลเยอร์ถูกเรียก มันจะส่งคืนข้อมูลที่ป้อน โดยแต่ละฟีเจอร์จะถูกทำให้เป็นมาตรฐานโดยอิสระ:
first = np.array(train_features[:1])
with np.printoptions(precision=2, suppress=True):
print('First example:', first)
print()
print('Normalized:', normalizer(first).numpy())
First example: [[ 4. 90. 75. 2125. 14.5 74. 0. 0. 1. ]] Normalized: [[-0.87 -1.01 -0.79 -1.03 -0.38 -0.52 -0.47 -0.5 0.78]]
การถดถอยเชิงเส้น
ก่อนสร้างแบบจำลองโครงข่ายประสาทลึก ให้เริ่มด้วยการถดถอยเชิงเส้นโดยใช้ตัวแปรหนึ่งตัวและหลายตัว
การถดถอยเชิงเส้นกับตัวแปรเดียว
เริ่มต้นด้วยการถดถอยเชิงเส้นตัวแปรเดียวเพื่อทำนาย 'MPG' จาก 'Horsepower'
การฝึกโมเดลด้วย tf.keras มักจะเริ่มต้นด้วยการกำหนดสถาปัตยกรรมโมเดล ใช้โมเดล tf.keras.Sequential ซึ่ง แสดงถึงลำดับของขั้นตอน
มีสองขั้นตอนในตัวแบบการถดถอยเชิงเส้นแบบตัวแปรเดียวของคุณ:
- ปรับคุณสมบัติอินพุต
'Horsepower'ให้เป็นมาตรฐานโดยใช้เลเยอร์การประมวลผลล่วงหน้าtf.keras.layers.Normalization - ใช้การแปลงเชิงเส้น (\(y = mx+b\)) เพื่อสร้าง 1 เอาต์พุตโดยใช้เลเยอร์เชิงเส้น (
tf.keras.layers.Dense)
จำนวน อินพุต สามารถกำหนดได้โดยอาร์กิวเมนต์ input_shape หรือโดยอัตโนมัติเมื่อรันโมเดลเป็นครั้งแรก
ขั้นแรก สร้างอาร์เรย์ NumPy ที่สร้างจากคุณสมบัติ 'Horsepower' จากนั้น ให้ยกตัวอย่าง tf.keras.layers.Normalization และปรับสถานะให้เข้ากับข้อมูล horsepower :
horsepower = np.array(train_features['Horsepower'])
horsepower_normalizer = layers.Normalization(input_shape=[1,], axis=None)
horsepower_normalizer.adapt(horsepower)
สร้างโมเดล Keras Sequential:
horsepower_model = tf.keras.Sequential([
horsepower_normalizer,
layers.Dense(units=1)
])
horsepower_model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense (Dense) (None, 1) 2
=================================================================
Total params: 5
Trainable params: 2
Non-trainable params: 3
_________________________________________________________________
ตัวยึดตำแหน่ง32 โมเดลนี้จะทำนาย 'MPG' จาก 'Horsepower'
เรียกใช้โมเดลที่ไม่ได้รับการฝึกฝนในค่า 'แรงม้า' 10 ค่าแรก ผลลัพธ์จะออกมาไม่ดี แต่สังเกตว่ามันมีรูปร่างที่คาดไว้ (10, 1) :
horsepower_model.predict(horsepower[:10])
array([[-1.186],
[-0.67 ],
[ 2.189],
[-1.662],
[-1.504],
[-0.59 ],
[-1.782],
[-1.504],
[-0.392],
[-0.67 ]], dtype=float32)
เมื่อสร้างโมเดลแล้ว ให้กำหนดค่าขั้นตอนการฝึกอบรมโดยใช้วิธี Keras Model.compile อาร์กิวเมนต์ที่สำคัญที่สุดในการรวบรวมคือการ loss และตัว optimizer เนื่องจากสิ่งเหล่านี้กำหนดสิ่งที่จะได้รับการปรับให้เหมาะสม ( mean_absolute_error ) และวิธี (โดยใช้ tf.keras.optimizers.Adam )
horsepower_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
ใช้ Keras Model.fit เพื่อดำเนินการฝึกอบรม 100 ยุค:
%%time
history = horsepower_model.fit(
train_features['Horsepower'],
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.79 s, sys: 797 ms, total: 5.59 s Wall time: 3.8 s
แสดงภาพความคืบหน้าการฝึกของโมเดลโดยใช้สถิติที่จัดเก็บไว้ในออบเจ็กต์ history :
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_loss(history):
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.ylim([0, 10])
plt.xlabel('Epoch')
plt.ylabel('Error [MPG]')
plt.legend()
plt.grid(True)
plot_loss(history)
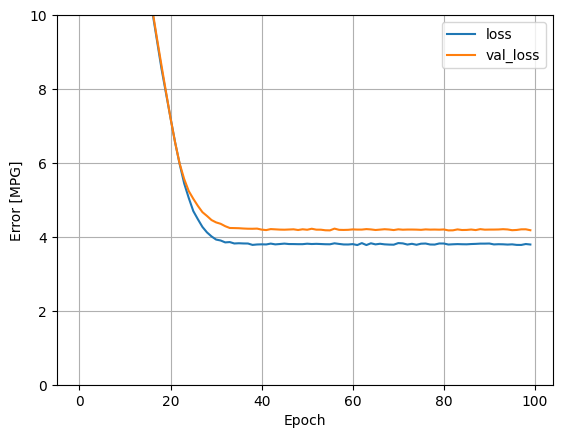
เก็บผลในชุดทดสอบในภายหลัง:
test_results = {}
test_results['horsepower_model'] = horsepower_model.evaluate(
test_features['Horsepower'],
test_labels, verbose=0)
เนื่องจากนี่เป็นการถดถอยตัวแปรเดียว จึงง่ายต่อการดูการคาดการณ์ของแบบจำลองว่าเป็นฟังก์ชันของอินพุต:
x = tf.linspace(0.0, 250, 251)
y = horsepower_model.predict(x)
def plot_horsepower(x, y):
plt.scatter(train_features['Horsepower'], train_labels, label='Data')
plt.plot(x, y, color='k', label='Predictions')
plt.xlabel('Horsepower')
plt.ylabel('MPG')
plt.legend()
plot_horsepower(x, y)
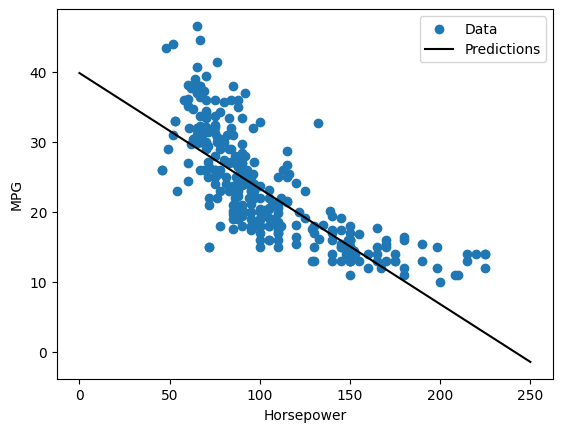
การถดถอยเชิงเส้นที่มีหลายอินพุต
คุณสามารถใช้การตั้งค่าที่เกือบจะเหมือนกันทั้งหมดเพื่อสร้างการคาดคะเนโดยอิงจากอินพุตหลายรายการ โมเดลนี้ยังคงใช้ \(y = mx+b\) เหมือนเดิม ยกเว้นว่า \(m\) เป็นเมทริกซ์ และ \(b\) เป็นเวกเตอร์
สร้างโมเดล Keras Sequential สองขั้นตอนอีกครั้งโดยที่เลเยอร์แรกเป็นแบบนอร์มัลไลเซอร์ ( normalizer tf.keras.layers.Normalization(axis=-1) ) ที่คุณกำหนดไว้ก่อนหน้านี้และปรับให้เข้ากับชุดข้อมูลทั้งหมด:
linear_model = tf.keras.Sequential([
normalizer,
layers.Dense(units=1)
])
เมื่อคุณเรียกใช้ Model.predict ในชุดอินพุต มันจะสร้างเอาต์พุต units=1 สำหรับแต่ละตัวอย่าง:
linear_model.predict(train_features[:10])
array([[ 0.441],
[ 1.522],
[ 0.188],
[ 1.169],
[ 0.058],
[ 0.965],
[ 0.034],
[-0.674],
[ 0.437],
[-0.37 ]], dtype=float32)
เมื่อคุณเรียกใช้โมเดล เมทริกซ์น้ำหนักจะถูกสร้างขึ้น ตรวจสอบว่าน้ำหนัก kernel ( \(m\) ใน \(y=mx+b\)) มีรูปร่างเป็น (9, 1) :
linear_model.layers[1].kernel
<tf.Variable 'dense_1/kernel:0' shape=(9, 1) dtype=float32, numpy=
array([[-0.702],
[ 0.307],
[ 0.114],
[ 0.233],
[ 0.244],
[ 0.322],
[-0.725],
[-0.151],
[ 0.407]], dtype=float32)>
กำหนดค่าโมเดลด้วย Keras Model.compile และฝึกด้วย Model.fit สำหรับ 100 epochs:
linear_model.compile(
optimizer=tf.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
%%time
history = linear_model.fit(
train_features,
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
CPU times: user 4.89 s, sys: 740 ms, total: 5.63 s Wall time: 3.75 s
การใช้อินพุตทั้งหมดในโมเดลการถดถอยนี้ทำให้การฝึกอบรมและข้อผิดพลาดในการตรวจสอบต่ำกว่ามาก กว่า horsepower_model ซึ่งมีอินพุตเดียว:
plot_loss(history)
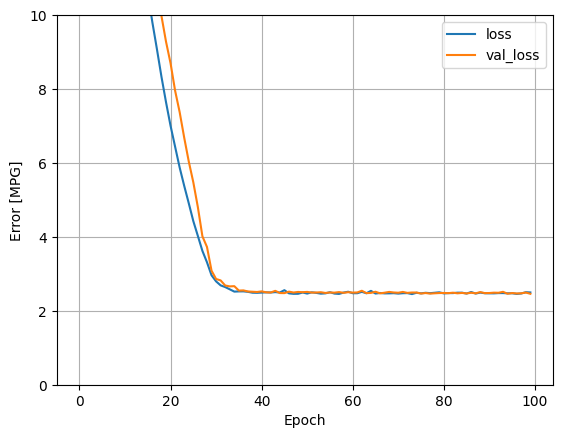
เก็บผลในชุดทดสอบในภายหลัง:
test_results['linear_model'] = linear_model.evaluate(
test_features, test_labels, verbose=0)
การถดถอยด้วยโครงข่ายประสาทลึก (DNN)
ในส่วนก่อนหน้านี้ คุณได้ปรับใช้โมเดลเชิงเส้นสองแบบสำหรับอินพุตเดี่ยวและหลายอินพุต
ที่นี่ คุณจะใช้โมเดล DNN แบบอินพุตเดียวและหลายอินพุต
โดยพื้นฐานแล้วโค้ดจะเหมือนกัน ยกเว้นโมเดลถูกขยายเพื่อรวมเลเยอร์ที่ไม่ใช่เชิงเส้น "ที่ซ่อนอยู่" บางอัน ชื่อ "ซ่อน" ในที่นี้หมายความว่าไม่ได้เชื่อมต่อโดยตรงกับอินพุตหรือเอาต์พุต
โมเดลเหล่านี้จะมีเลเยอร์มากกว่าโมเดลเชิงเส้นเล็กน้อย:
- เลเยอร์การทำให้เป็น
normalizerเหมือนเมื่อก่อน (ด้วยhorsepower_normalizerสำหรับโมเดลอินพุตเดียวและนอร์มัลไลเซอร์สำหรับโมเดลหลายอินพุต) - เลเยอร์
Denseที่ไม่เป็นเชิงเส้นสองชั้นที่ซ่อนอยู่ด้วยฟังก์ชันการเปิดใช้งาน ReLU (relu) ที่ไม่เป็นเชิงเส้น - เลเยอร์เอาต์พุตเดี่ยวแบบเส้นตรง
Dense
ทั้งสองรุ่นจะใช้ขั้นตอนการฝึกอบรมเดียวกัน ดังนั้นวิธีการ compile จึงรวมอยู่ในฟังก์ชัน build_and_compile_model ด้านล่าง
def build_and_compile_model(norm):
model = keras.Sequential([
norm,
layers.Dense(64, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
model.compile(loss='mean_absolute_error',
optimizer=tf.keras.optimizers.Adam(0.001))
return model
การถดถอยโดยใช้ DNN และอินพุตเดียว
สร้างโมเดล DNN ที่มีเพียง 'Horsepower' เป็นอินพุตและ horsepower_normalizer (กำหนดไว้ก่อนหน้านี้) เป็นเลเยอร์การทำให้เป็นมาตรฐาน:
dnn_horsepower_model = build_and_compile_model(horsepower_normalizer)
โมเดลนี้มีพารามิเตอร์ที่ฝึกได้ค่อนข้างน้อยกว่าโมเดลเชิงเส้น:
dnn_horsepower_model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization_1 (Normalizat (None, 1) 3
ion)
dense_2 (Dense) (None, 64) 128
dense_3 (Dense) (None, 64) 4160
dense_4 (Dense) (None, 1) 65
=================================================================
Total params: 4,356
Trainable params: 4,353
Non-trainable params: 3
_________________________________________________________________
ฝึกโมเดลด้วย Keras Model.fit :
%%time
history = dnn_horsepower_model.fit(
train_features['Horsepower'],
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.07 s, sys: 691 ms, total: 5.76 s Wall time: 3.92 sตัวยึดตำแหน่ง60
โมเดลนี้ทำได้ดีกว่า horsepower_model แบบ single-input แบบ single-input เล็กน้อย:
plot_loss(history)
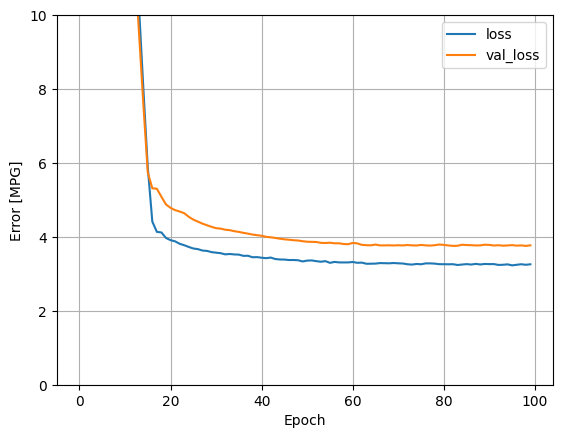
หากคุณพล็อตการคาดคะเนเป็นฟังก์ชันของ 'Horsepower' คุณควรสังเกตว่าโมเดลนี้ใช้ประโยชน์จากความไม่เชิงเส้นของเลเยอร์ที่ซ่อนอยู่ได้อย่างไร:
x = tf.linspace(0.0, 250, 251)
y = dnn_horsepower_model.predict(x)
plot_horsepower(x, y)
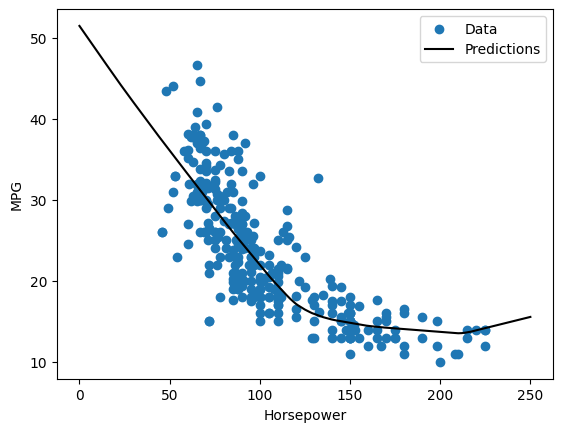
เก็บผลในชุดทดสอบในภายหลัง:
test_results['dnn_horsepower_model'] = dnn_horsepower_model.evaluate(
test_features['Horsepower'], test_labels,
verbose=0)
การถดถอยโดยใช้ DNN และอินพุตหลายตัว
ทำซ้ำขั้นตอนก่อนหน้าโดยใช้อินพุตทั้งหมด ประสิทธิภาพของแบบจำลองดีขึ้นเล็กน้อยในชุดข้อมูลการตรวจสอบ
dnn_model = build_and_compile_model(normalizer)
dnn_model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
normalization (Normalizatio (None, 9) 19
n)
dense_5 (Dense) (None, 64) 640
dense_6 (Dense) (None, 64) 4160
dense_7 (Dense) (None, 1) 65
=================================================================
Total params: 4,884
Trainable params: 4,865
Non-trainable params: 19
_________________________________________________________________
%%time
history = dnn_model.fit(
train_features,
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
CPU times: user 5.08 s, sys: 725 ms, total: 5.8 s Wall time: 3.94 s
plot_loss(history)
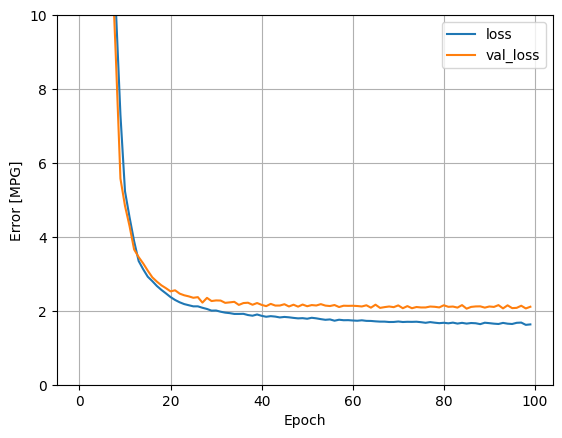
เก็บผลในชุดทดสอบ:
test_results['dnn_model'] = dnn_model.evaluate(test_features, test_labels, verbose=0)
ประสิทธิภาพ
เนื่องจากทุกรุ่นได้รับการฝึกอบรม คุณสามารถตรวจสอบประสิทธิภาพของชุดทดสอบได้:
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
ผลลัพธ์เหล่านี้ตรงกับข้อผิดพลาดในการตรวจสอบที่สังเกตได้ระหว่างการฝึก
ทำนายฝัน
ตอนนี้คุณสามารถคาดการณ์ด้วย dnn_model ในชุดการทดสอบโดยใช้ Keras Model.predict และตรวจสอบการสูญเสีย:
test_predictions = dnn_model.predict(test_features).flatten()
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
lims = [0, 50]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)

ดูเหมือนว่าโมเดลคาดการณ์ได้ดีพอสมควร
ตอนนี้ ตรวจสอบการกระจายข้อผิดพลาด:
error = test_predictions - test_labels
plt.hist(error, bins=25)
plt.xlabel('Prediction Error [MPG]')
_ = plt.ylabel('Count')
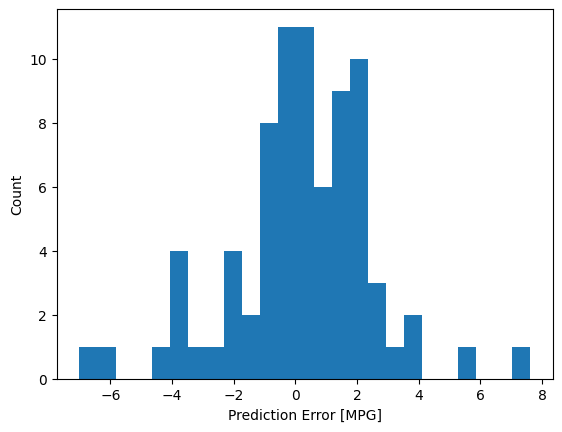
หากคุณพอใจกับโมเดลนี้ ให้บันทึกไว้เพื่อใช้ในภายหลังด้วย Model.save :
dnn_model.save('dnn_model')
2022-01-26 07:26:13.372245: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: dnn_model/assets
หากคุณรีโหลดโมเดล มันจะให้ผลลัพธ์ที่เหมือนกัน:
reloaded = tf.keras.models.load_model('dnn_model')
test_results['reloaded'] = reloaded.evaluate(
test_features, test_labels, verbose=0)
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
บทสรุป
สมุดบันทึกนี้แนะนำเทคนิคบางประการเพื่อจัดการกับปัญหาการถดถอย ต่อไปนี้เป็นเคล็ดลับเพิ่มเติมที่อาจช่วยได้:
- ข้อผิดพลาดกำลังสองเฉลี่ย (MSE) (
tf.losses.MeanSquaredError) และข้อผิดพลาดแบบสัมบูรณ์เฉลี่ย (MAE) (tf.losses.MeanAbsoluteError) เป็นฟังก์ชันการสูญเสียทั่วไปที่ใช้สำหรับปัญหาการถดถอย MAE มีความไวต่อค่าผิดปกติน้อยกว่า ฟังก์ชันการสูญเสียต่างๆ ใช้สำหรับปัญหาการจำแนกประเภท - ในทำนองเดียวกัน ตัวชี้วัดการประเมินที่ใช้สำหรับการถดถอยแตกต่างจากการจัดประเภท
- เมื่อคุณลักษณะข้อมูลป้อนที่เป็นตัวเลขมีค่าที่มีช่วงต่างกัน คุณลักษณะแต่ละรายการควรได้รับการปรับขนาดอย่างอิสระเพื่อให้อยู่ในช่วงเดียวกัน
- Overfitting เป็นปัญหาทั่วไปสำหรับโมเดล DNN แม้ว่าจะไม่ใช่ปัญหาสำหรับบทช่วยสอนนี้ ไปที่บทแนะนำ Overfit และ underfit เพื่อรับความช่วยเหลือเพิ่มเติมเกี่ยวกับเรื่องนี้
# MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
