 مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
این آموزش نحوه طبقه بندی مجموعه داده های بسیار نامتعادل را نشان می دهد که در آن تعداد نمونه ها در یک کلاس بسیار بیشتر از نمونه های کلاس دیگر است. شما با مجموعه داده شناسایی تقلب در کارت اعتباری که در Kaggle میزبانی شده است کار خواهید کرد. هدف این است که از مجموع 284807 تراکنش، تنها 492 تراکنش جعلی را شناسایی کنیم. شما از Keras برای تعریف وزن مدل و کلاس استفاده خواهید کرد تا به مدل کمک کند تا از داده های نامتعادل یاد بگیرد. .
این آموزش حاوی کد کاملی است برای:
- یک فایل CSV را با استفاده از پاندا بارگیری کنید.
- مجموعههای قطار، اعتبارسنجی و آزمایش ایجاد کنید.
- یک مدل را با استفاده از Keras (از جمله تنظیم وزن کلاس) تعریف و آموزش دهید.
- مدل را با استفاده از معیارهای مختلف (از جمله دقت و یادآوری) ارزیابی کنید.
- تکنیک های رایج برای مقابله با داده های نامتعادل مانند:
- وزن بندی کلاس
- نمونه برداری بیش از حد
برپایی
import tensorflow as tf
from tensorflow import keras
import os
import tempfile
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
پردازش و کاوش داده ها
مجموعه داده های کلاهبرداری کارت اعتباری Kaggle را دانلود کنید
Pandas یک کتابخانه پایتون با بسیاری از ابزارهای مفید برای بارگیری و کار با داده های ساخت یافته است. می توان از آن برای دانلود فایل های CSV در یک Pandas DataFrame استفاده کرد.
file = tf.keras.utils
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()
raw_df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe()
عدم تعادل برچسب کلاس را بررسی کنید
بیایید به عدم تعادل مجموعه داده نگاه کنیم:
neg, pos = np.bincount(raw_df['Class'])
total = neg + pos
print('Examples:\n Total: {}\n Positive: {} ({:.2f}% of total)\n'.format(
total, pos, 100 * pos / total))
Examples:
Total: 284807
Positive: 492 (0.17% of total)
این بخش کوچکی از نمونه های مثبت را نشان می دهد.
داده ها را تمیز، تقسیم و عادی کنید
داده های خام چند مشکل دارد. ابتدا ستونهای Time و Amount برای استفاده مستقیم بسیار متغیر هستند. ستون Time را رها کنید (چون معنی آن مشخص نیست) و گزارش ستون Amount را بردارید تا محدوده آن را کاهش دهید.
cleaned_df = raw_df.copy()
# You don't want the `Time` column.
cleaned_df.pop('Time')
# The `Amount` column covers a huge range. Convert to log-space.
eps = 0.001 # 0 => 0.1¢
cleaned_df['Log Ammount'] = np.log(cleaned_df.pop('Amount')+eps)
مجموعه داده را به مجموعه های قطار، اعتبار سنجی و آزمایش تقسیم کنید. مجموعه اعتبارسنجی در طول برازش مدل برای ارزیابی ضرر و هر معیاری استفاده میشود، اما مدل با این دادهها تناسب ندارد. مجموعه تست در مرحله آموزش کاملاً استفاده نشده است و فقط در پایان برای ارزیابی میزان تعمیم مدل به داده های جدید استفاده می شود. این امر به ویژه در مورد مجموعه داده های نامتعادل که در آن بیش از حد برازش یک نگرانی مهم از فقدان داده های آموزشی است، مهم است.
# Use a utility from sklearn to split and shuffle your dataset.
train_df, test_df = train_test_split(cleaned_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)
# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
bool_train_labels = train_labels != 0
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))
train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)
با استفاده از sklearn StandardScaler ویژگی های ورودی را عادی کنید. با این کار میانگین 0 و انحراف استاندارد 1 تنظیم می شود.
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)
train_features = np.clip(train_features, -5, 5)
val_features = np.clip(val_features, -5, 5)
test_features = np.clip(test_features, -5, 5)
print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)
print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)
Training labels shape: (182276,) Validation labels shape: (45569,) Test labels shape: (56962,) Training features shape: (182276, 29) Validation features shape: (45569, 29) Test features shape: (56962, 29)
به توزیع داده ها نگاه کنید
سپس توزیع مثال های مثبت و منفی را بر روی چند ویژگی مقایسه کنید. سوالات خوبی که باید در این مرحله از خود بپرسید عبارتند از:
- آیا این توزیع ها منطقی هستند؟
- آره. شما ورودی را عادی کرده اید و اینها عمدتاً در محدوده
+/- 2متمرکز هستند.
- آره. شما ورودی را عادی کرده اید و اینها عمدتاً در محدوده
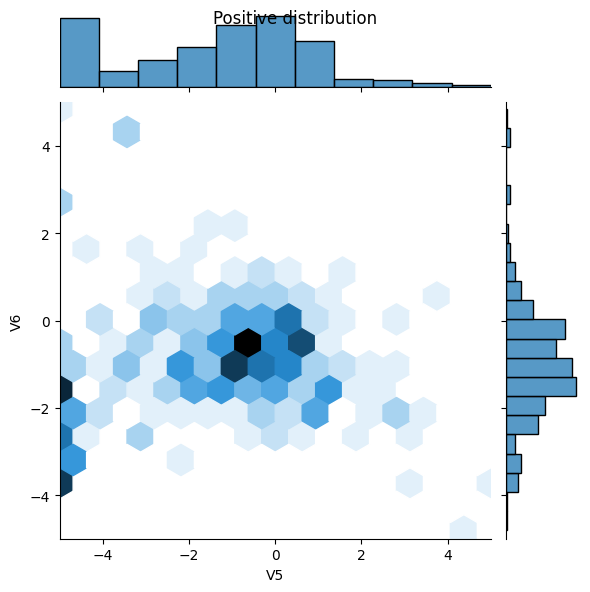
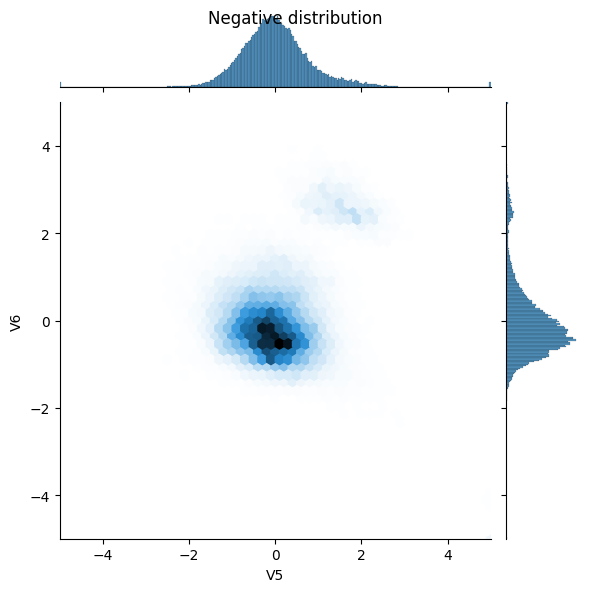
- آیا می توانید تفاوت بین توزیع ها را ببینید؟
- بله، مثالهای مثبت دارای نرخ بسیار بالاتری از مقادیر شدید هستند.
pos_df = pd.DataFrame(train_features[ bool_train_labels], columns=train_df.columns)
neg_df = pd.DataFrame(train_features[~bool_train_labels], columns=train_df.columns)
sns.jointplot(x=pos_df['V5'], y=pos_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
plt.suptitle("Positive distribution")
sns.jointplot(x=neg_df['V5'], y=neg_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
_ = plt.suptitle("Negative distribution")
مدل و معیارها را تعریف کنید
تابعی را تعریف کنید که یک شبکه عصبی ساده با یک لایه پنهان متصل متراکم، یک لایه حذفی برای کاهش بیشبرازش و یک لایه سیگموئید خروجی ایجاد میکند که احتمال تقلبی بودن یک تراکنش را برمیگرداند:
METRICS = [
keras.metrics.TruePositives(name='tp'),
keras.metrics.FalsePositives(name='fp'),
keras.metrics.TrueNegatives(name='tn'),
keras.metrics.FalseNegatives(name='fn'),
keras.metrics.BinaryAccuracy(name='accuracy'),
keras.metrics.Precision(name='precision'),
keras.metrics.Recall(name='recall'),
keras.metrics.AUC(name='auc'),
keras.metrics.AUC(name='prc', curve='PR'), # precision-recall curve
]
def make_model(metrics=METRICS, output_bias=None):
if output_bias is not None:
output_bias = tf.keras.initializers.Constant(output_bias)
model = keras.Sequential([
keras.layers.Dense(
16, activation='relu',
input_shape=(train_features.shape[-1],)),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid',
bias_initializer=output_bias),
])
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.BinaryCrossentropy(),
metrics=metrics)
return model
درک معیارهای مفید
توجه داشته باشید که چند معیار تعریف شده در بالا وجود دارد که می تواند توسط مدل محاسبه شود که هنگام ارزیابی عملکرد مفید خواهد بود.
- موارد منفی کاذب و مثبت کاذب نمونه هایی هستند که به اشتباه طبقه بندی شده اند
- منفی واقعی و مثبت واقعی نمونه هایی هستند که به درستی طبقه بندی شده اند
- دقت درصد نمونه هایی است که به درستی طبقه بندی شده اند > \(\frac{\text{true samples} }{\text{total samples} }\)
- دقت درصدی از موارد مثبت پیش بینی شده است که به درستی طبقه بندی شده اند > \(\frac{\text{true positives} }{\text{true positives + false positives} }\)
- یادآوری درصد موارد مثبت واقعی است که به درستی طبقه بندی شده اند > \(\frac{\text{true positives} }{\text{true positives + false negatives} }\)
- AUC به ناحیه زیر منحنی یک منحنی مشخصه عملکرد گیرنده (ROC-AUC) اشاره دارد. این معیار برابر با احتمال این است که یک طبقهبندی کننده یک نمونه مثبت تصادفی را بالاتر از یک نمونه منفی تصادفی رتبهبندی کند.
- AUPRC به ناحیه زیر منحنی منحنی فراخوان دقیق اشاره دارد. این متریک جفتهای فراخوان دقیق را برای آستانههای احتمالی مختلف محاسبه میکند.
بیشتر بخوانید:
- درست در مقابل نادرست و مثبت در مقابل منفی
- دقت
- دقت و یادآوری
- ROC-AUC
- رابطه بین منحنی های دقیق-یادآوری و ROC
مدل پایه
مدل را بسازید
اکنون با استفاده از تابعی که قبلا تعریف شده بود، مدل خود را ایجاد و آموزش دهید. توجه داشته باشید که مدل با استفاده از اندازه دسته ای بزرگتر از اندازه پیش فرض 2048 مناسب است، این برای اطمینان از اینکه هر دسته شانس مناسبی برای داشتن چند نمونه مثبت دارد مهم است. اگر اندازه دسته خیلی کوچک بود، احتمالاً هیچ تراکنش متقلبانه ای برای یادگیری نداشتند.
EPOCHS = 100
BATCH_SIZE = 2048
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_prc',
verbose=1,
patience=10,
mode='max',
restore_best_weights=True)
model = make_model()
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 16) 480
dropout (Dropout) (None, 16) 0
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 497
Trainable params: 497
Non-trainable params: 0
_________________________________________________________________
مدل را آزمایش کنید:
model.predict(train_features[:10])
array([[0.9466284 ],
[0.7211031 ],
[0.60527885],
[0.8335568 ],
[0.5909625 ],
[0.6751574 ],
[0.6623665 ],
[0.81066036],
[0.50712407],
[0.8296292 ]], dtype=float32)
اختیاری: تعصب اولیه صحیح را تنظیم کنید.
این حدس های اولیه عالی نیستند. می دانید که مجموعه داده نامتعادل است. بایاس لایه خروجی را طوری تنظیم کنید که منعکس شود (نگاه کنید به: دستور العملی برای آموزش شبکه های عصبی: "init well" ). این می تواند به همگرایی اولیه کمک کند.
با مقداردهی اولیه بایاس پیشفرض، ضرر باید در حدود math.log(2) = 0.69314
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 1.2781
سوگیری صحیح برای تنظیم را می توان از موارد زیر استخراج کرد:
\[ p_0 = pos/(pos + neg) = 1/(1+e^{-b_0}) \]
\[ b_0 = -log_e(1/p_0 - 1) \]
\[ b_0 = log_e(pos/neg)\]
initial_bias = np.log([pos/neg])
initial_bias
array([-6.35935934])
آن را به عنوان سوگیری اولیه تنظیم کنید، و مدل حدس های اولیه بسیار معقول تری را ارائه می دهد.
باید نزدیک باشد: pos/total = 0.0018
model = make_model(output_bias=initial_bias)
model.predict(train_features[:10])
array([[2.3598122e-05],
[1.5476024e-03],
[6.8338902e-04],
[9.4873342e-04],
[1.0742771e-03],
[7.7475846e-04],
[1.2199467e-03],
[5.5399281e-04],
[1.6213538e-03],
[3.0470363e-04]], dtype=float32)
با این مقداردهی اولیه، ضرر اولیه باید تقریباً باشد:
\[-p_0log(p_0)-(1-p_0)log(1-p_0) = 0.01317\]
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 0.0200
این تلفات اولیه حدود 50 برابر کمتر از زمانی است که با مقداردهی اولیه ساده بود.
به این ترتیب مدل نیازی ندارد که چند دوره اول را صرف یادگیری این باشد که نمونه های مثبت بعید است. این همچنین خواندن نمودارهای از دست دادن در طول تمرین را آسان تر می کند.
وزنه های اولیه را چک کنید
برای مقایسه بیشتر دورههای آموزشی مختلف، وزنهای این مدل اولیه را در یک فایل بازرسی نگه دارید و قبل از تمرین آنها را در هر مدل بارگذاری کنید:
initial_weights = os.path.join(tempfile.mkdtemp(), 'initial_weights')
model.save_weights(initial_weights)
تأیید کنید که رفع سوگیری کمک می کند
قبل از حرکت، سریع تأیید کنید که اولیه سازی دقیق سوگیری واقعا کمک کرده است.
مدل را برای 20 دوره با و بدون این مقداردهی اولیه دقیق آموزش دهید و تلفات را مقایسه کنید:
model = make_model()
model.load_weights(initial_weights)
model.layers[-1].bias.assign([0.0])
zero_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
model = make_model()
model.load_weights(initial_weights)
careful_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
def plot_loss(history, label, n):
# Use a log scale on y-axis to show the wide range of values.
plt.semilogy(history.epoch, history.history['loss'],
color=colors[n], label='Train ' + label)
plt.semilogy(history.epoch, history.history['val_loss'],
color=colors[n], label='Val ' + label,
linestyle="--")
plt.xlabel('Epoch')
plt.ylabel('Loss')
plot_loss(zero_bias_history, "Zero Bias", 0)
plot_loss(careful_bias_history, "Careful Bias", 1)
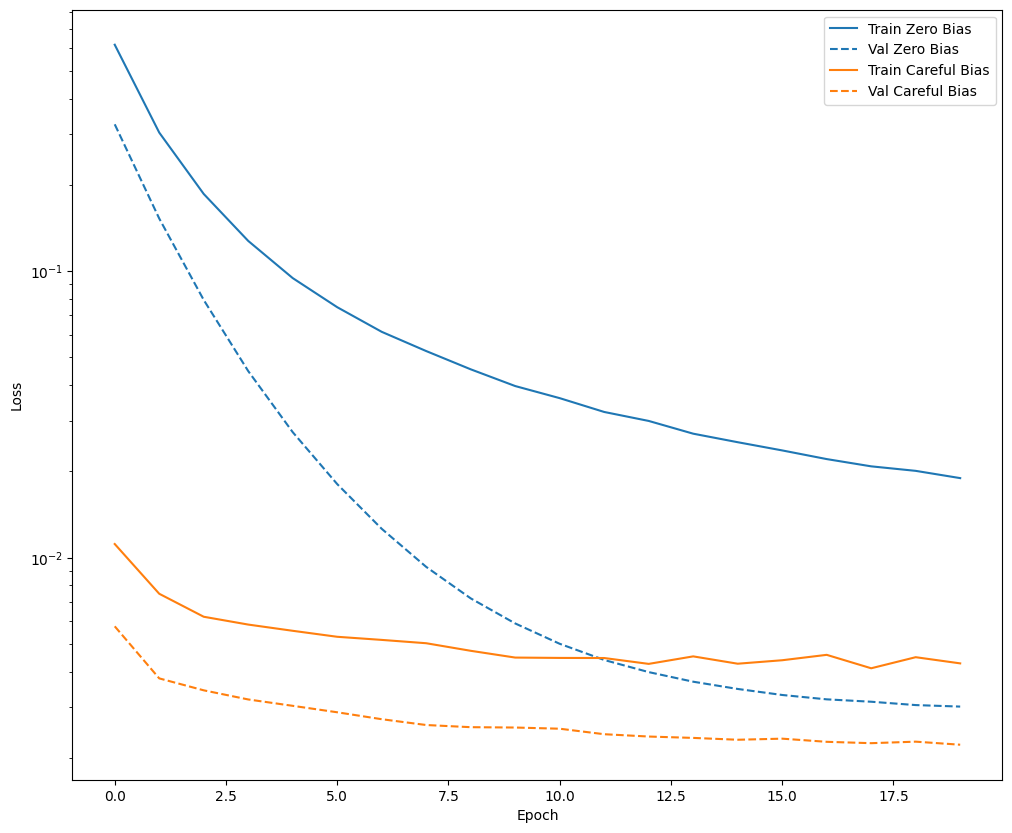
شکل بالا به وضوح نشان می دهد: از نظر از دست دادن اعتبار سنجی، در این مشکل، این مقداردهی اولیه دقیق یک مزیت واضح به دست می دهد.
مدل را آموزش دهید
model = make_model()
model.load_weights(initial_weights)
baseline_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels))
Epoch 1/100 90/90 [==============================] - 3s 15ms/step - loss: 0.0161 - tp: 64.0000 - fp: 9.0000 - tn: 227425.0000 - fn: 347.0000 - accuracy: 0.9984 - precision: 0.8767 - recall: 0.1557 - auc: 0.6148 - prc: 0.1692 - val_loss: 0.0115 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7205 - val_prc: 0.2571 Epoch 2/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0087 - tp: 49.0000 - fp: 11.0000 - tn: 181940.0000 - fn: 276.0000 - accuracy: 0.9984 - precision: 0.8167 - recall: 0.1508 - auc: 0.8085 - prc: 0.3735 - val_loss: 0.0054 - val_tp: 35.0000 - val_fp: 6.0000 - val_tn: 45477.0000 - val_fn: 51.0000 - val_accuracy: 0.9987 - val_precision: 0.8537 - val_recall: 0.4070 - val_auc: 0.9065 - val_prc: 0.6598 Epoch 3/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0061 - tp: 126.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 199.0000 - accuracy: 0.9988 - precision: 0.8235 - recall: 0.3877 - auc: 0.8997 - prc: 0.6187 - val_loss: 0.0046 - val_tp: 55.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 31.0000 - val_accuracy: 0.9991 - val_precision: 0.8730 - val_recall: 0.6395 - val_auc: 0.9063 - val_prc: 0.6941 Epoch 4/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 172.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 153.0000 - accuracy: 0.9990 - precision: 0.8473 - recall: 0.5292 - auc: 0.9068 - prc: 0.6448 - val_loss: 0.0044 - val_tp: 58.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 28.0000 - val_accuracy: 0.9992 - val_precision: 0.8788 - val_recall: 0.6744 - val_auc: 0.9064 - val_prc: 0.7114 Epoch 5/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0056 - tp: 167.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 158.0000 - accuracy: 0.9990 - precision: 0.8477 - recall: 0.5138 - auc: 0.9134 - prc: 0.6215 - val_loss: 0.0043 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7181 Epoch 6/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 193.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 132.0000 - accuracy: 0.9991 - precision: 0.8733 - recall: 0.5938 - auc: 0.9198 - prc: 0.6760 - val_loss: 0.0042 - val_tp: 59.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 27.0000 - val_accuracy: 0.9992 - val_precision: 0.8806 - val_recall: 0.6860 - val_auc: 0.9064 - val_prc: 0.7370 Epoch 7/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 183.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 142.0000 - accuracy: 0.9991 - precision: 0.8592 - recall: 0.5631 - auc: 0.9202 - prc: 0.6737 - val_loss: 0.0042 - val_tp: 60.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6977 - val_auc: 0.9064 - val_prc: 0.7463 Epoch 8/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 171.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 154.0000 - accuracy: 0.9990 - precision: 0.8465 - recall: 0.5262 - auc: 0.9156 - prc: 0.6574 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7480 Epoch 9/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 196.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8711 - recall: 0.6031 - auc: 0.9218 - prc: 0.6799 - val_loss: 0.0041 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9065 - val_prc: 0.7550 Epoch 10/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0050 - tp: 173.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 152.0000 - accuracy: 0.9990 - precision: 0.8650 - recall: 0.5323 - auc: 0.9048 - prc: 0.6520 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9122 - val_prc: 0.7598 Epoch 11/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0048 - tp: 190.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8597 - recall: 0.5846 - auc: 0.9172 - prc: 0.6779 - val_loss: 0.0040 - val_tp: 63.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8750 - val_recall: 0.7326 - val_auc: 0.9065 - val_prc: 0.7595 Epoch 12/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 192.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 133.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.5908 - auc: 0.9281 - prc: 0.7312 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9123 - val_prc: 0.7648 Epoch 13/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 185.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 140.0000 - accuracy: 0.9991 - precision: 0.8565 - recall: 0.5692 - auc: 0.9328 - prc: 0.7222 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7615 Epoch 14/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0047 - tp: 183.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 142.0000 - accuracy: 0.9990 - precision: 0.8472 - recall: 0.5631 - auc: 0.9295 - prc: 0.6770 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7670 Epoch 15/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0043 - tp: 194.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8700 - recall: 0.5969 - auc: 0.9344 - prc: 0.7233 - val_loss: 0.0040 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7672 Epoch 16/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 207.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8697 - recall: 0.6369 - auc: 0.9329 - prc: 0.7194 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8767 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7694 Epoch 17/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0042 - tp: 190.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 135.0000 - accuracy: 0.9991 - precision: 0.8716 - recall: 0.5846 - auc: 0.9345 - prc: 0.7265 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7705 Epoch 18/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8622 - recall: 0.5969 - auc: 0.9344 - prc: 0.7199 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7725 Epoch 19/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0041 - tp: 205.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8613 - recall: 0.6308 - auc: 0.9346 - prc: 0.7266 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7739 Epoch 20/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 207.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8809 - recall: 0.6369 - auc: 0.9421 - prc: 0.7634 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8784 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7729 Epoch 21/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0040 - tp: 204.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8644 - recall: 0.6277 - auc: 0.9360 - prc: 0.7340 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7756 Epoch 22/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 207.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 118.0000 - accuracy: 0.9992 - precision: 0.8884 - recall: 0.6369 - auc: 0.9328 - prc: 0.7277 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7773 Epoch 23/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0041 - tp: 191.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8527 - recall: 0.5877 - auc: 0.9375 - prc: 0.7280 - val_loss: 0.0038 - val_tp: 62.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8857 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7790 Epoch 24/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 196.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 129.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6031 - auc: 0.9375 - prc: 0.7466 - val_loss: 0.0038 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9123 - val_prc: 0.7762 Epoch 25/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 204.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8681 - recall: 0.6277 - auc: 0.9467 - prc: 0.7480 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9123 - val_prc: 0.7789 Epoch 26/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0040 - tp: 194.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 131.0000 - accuracy: 0.9991 - precision: 0.8661 - recall: 0.5969 - auc: 0.9360 - prc: 0.7292 - val_loss: 0.0038 - val_tp: 60.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8955 - val_recall: 0.6977 - val_auc: 0.9123 - val_prc: 0.7783 Epoch 27/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8776 - recall: 0.6400 - auc: 0.9376 - prc: 0.7632 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7772 Epoch 28/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 202.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 123.0000 - accuracy: 0.9991 - precision: 0.8596 - recall: 0.6215 - auc: 0.9408 - prc: 0.7638 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7808 Epoch 29/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 214.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8807 - recall: 0.6585 - auc: 0.9347 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7806 Epoch 30/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0039 - tp: 197.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 128.0000 - accuracy: 0.9991 - precision: 0.8640 - recall: 0.6062 - auc: 0.9346 - prc: 0.7489 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7804 Epoch 31/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 213.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 112.0000 - accuracy: 0.9992 - precision: 0.8659 - recall: 0.6554 - auc: 0.9407 - prc: 0.7615 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7809 Epoch 32/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9407 - prc: 0.7626 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7821 Epoch 33/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 210.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 115.0000 - accuracy: 0.9992 - precision: 0.8787 - recall: 0.6462 - auc: 0.9392 - prc: 0.7642 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8732 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7826 Epoch 34/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 217.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8857 - recall: 0.6677 - auc: 0.9423 - prc: 0.7759 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7830 Epoch 35/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 35.0000 - tn: 181916.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8566 - recall: 0.6431 - auc: 0.9407 - prc: 0.7381 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836 Epoch 36/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 204.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 121.0000 - accuracy: 0.9992 - precision: 0.8831 - recall: 0.6277 - auc: 0.9407 - prc: 0.7587 - val_loss: 0.0038 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840 Epoch 37/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8672 - recall: 0.6431 - auc: 0.9345 - prc: 0.7386 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7849 Epoch 38/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 198.0000 - fp: 33.0000 - tn: 181918.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8571 - recall: 0.6092 - auc: 0.9454 - prc: 0.7488 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7844 Epoch 39/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 209.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8782 - recall: 0.6431 - auc: 0.9407 - prc: 0.7419 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7840 Epoch 40/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 198.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 127.0000 - accuracy: 0.9991 - precision: 0.8761 - recall: 0.6092 - auc: 0.9546 - prc: 0.7644 - val_loss: 0.0039 - val_tp: 65.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 21.0000 - val_accuracy: 0.9993 - val_precision: 0.8667 - val_recall: 0.7558 - val_auc: 0.9124 - val_prc: 0.7835 Epoch 41/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0038 - tp: 209.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8745 - recall: 0.6431 - auc: 0.9377 - prc: 0.7587 - val_loss: 0.0039 - val_tp: 63.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 23.0000 - val_accuracy: 0.9993 - val_precision: 0.8630 - val_recall: 0.7326 - val_auc: 0.9124 - val_prc: 0.7827 Epoch 42/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0038 - tp: 195.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8667 - recall: 0.6000 - auc: 0.9345 - prc: 0.7436 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7834 Epoch 43/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8655 - recall: 0.6338 - auc: 0.9500 - prc: 0.7699 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7836 Epoch 44/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8927 - recall: 0.6400 - auc: 0.9438 - prc: 0.7625 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7841 Epoch 45/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 205.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 120.0000 - accuracy: 0.9992 - precision: 0.8686 - recall: 0.6308 - auc: 0.9422 - prc: 0.7519 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7847 Epoch 46/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0037 - tp: 206.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8766 - recall: 0.6338 - auc: 0.9423 - prc: 0.7529 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9124 - val_prc: 0.7843 Epoch 47/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 219.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8866 - recall: 0.6738 - auc: 0.9377 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 8.0000 - val_tn: 45475.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8841 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7871 Epoch 48/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 206.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8729 - recall: 0.6338 - auc: 0.9393 - prc: 0.7676 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7854 Epoch 49/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 215.0000 - fp: 29.0000 - tn: 181922.0000 - fn: 110.0000 - accuracy: 0.9992 - precision: 0.8811 - recall: 0.6615 - auc: 0.9407 - prc: 0.7618 - val_loss: 0.0039 - val_tp: 62.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8611 - val_recall: 0.7209 - val_auc: 0.9125 - val_prc: 0.7855 Epoch 50/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 214.0000 - fp: 32.0000 - tn: 181919.0000 - fn: 111.0000 - accuracy: 0.9992 - precision: 0.8699 - recall: 0.6585 - auc: 0.9377 - prc: 0.7727 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7858 Epoch 51/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 219.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 106.0000 - accuracy: 0.9993 - precision: 0.8795 - recall: 0.6738 - auc: 0.9393 - prc: 0.7889 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7876 Epoch 52/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 217.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 108.0000 - accuracy: 0.9993 - precision: 0.8967 - recall: 0.6677 - auc: 0.9439 - prc: 0.7812 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7887 Epoch 53/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 206.0000 - fp: 28.0000 - tn: 181923.0000 - fn: 119.0000 - accuracy: 0.9992 - precision: 0.8803 - recall: 0.6338 - auc: 0.9362 - prc: 0.7734 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7873 Epoch 54/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 223.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 102.0000 - accuracy: 0.9993 - precision: 0.8814 - recall: 0.6862 - auc: 0.9438 - prc: 0.7677 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7877 Epoch 55/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 220.0000 - fp: 26.0000 - tn: 181925.0000 - fn: 105.0000 - accuracy: 0.9993 - precision: 0.8943 - recall: 0.6769 - auc: 0.9439 - prc: 0.7866 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886 Epoch 56/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 209.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 116.0000 - accuracy: 0.9992 - precision: 0.8970 - recall: 0.6431 - auc: 0.9392 - prc: 0.7613 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 7.0000 - val_tn: 45476.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8971 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7886 Epoch 57/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0033 - tp: 221.0000 - fp: 23.0000 - tn: 181928.0000 - fn: 104.0000 - accuracy: 0.9993 - precision: 0.9057 - recall: 0.6800 - auc: 0.9516 - prc: 0.7954 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7873 Epoch 58/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 208.0000 - fp: 27.0000 - tn: 181924.0000 - fn: 117.0000 - accuracy: 0.9992 - precision: 0.8851 - recall: 0.6400 - auc: 0.9485 - prc: 0.7746 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7875 Epoch 59/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 216.0000 - fp: 30.0000 - tn: 181921.0000 - fn: 109.0000 - accuracy: 0.9992 - precision: 0.8780 - recall: 0.6646 - auc: 0.9531 - prc: 0.7928 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7883 Epoch 60/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0035 - tp: 211.0000 - fp: 31.0000 - tn: 181920.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8719 - recall: 0.6492 - auc: 0.9469 - prc: 0.7808 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9125 - val_prc: 0.7882 Epoch 61/100 90/90 [==============================] - 1s 7ms/step - loss: 0.0036 - tp: 201.0000 - fp: 24.0000 - tn: 181927.0000 - fn: 124.0000 - accuracy: 0.9992 - precision: 0.8933 - recall: 0.6185 - auc: 0.9424 - prc: 0.7720 - val_loss: 0.0039 - val_tp: 61.0000 - val_fp: 9.0000 - val_tn: 45474.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8714 - val_recall: 0.7093 - val_auc: 0.9124 - val_prc: 0.7881 Epoch 62/100 81/90 [==========================>...] - ETA: 0s - loss: 0.0034 - tp: 196.0000 - fp: 21.0000 - tn: 165565.0000 - fn: 106.0000 - accuracy: 0.9992 - precision: 0.9032 - recall: 0.6490 - auc: 0.9413 - prc: 0.7849Restoring model weights from the end of the best epoch: 52. 90/90 [==============================] - 1s 7ms/step - loss: 0.0034 - tp: 211.0000 - fp: 25.0000 - tn: 181926.0000 - fn: 114.0000 - accuracy: 0.9992 - precision: 0.8941 - recall: 0.6492 - auc: 0.9423 - prc: 0.7828 - val_loss: 0.0039 - val_tp: 64.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 22.0000 - val_accuracy: 0.9993 - val_precision: 0.8649 - val_recall: 0.7442 - val_auc: 0.9124 - val_prc: 0.7860 Epoch 62: early stopping
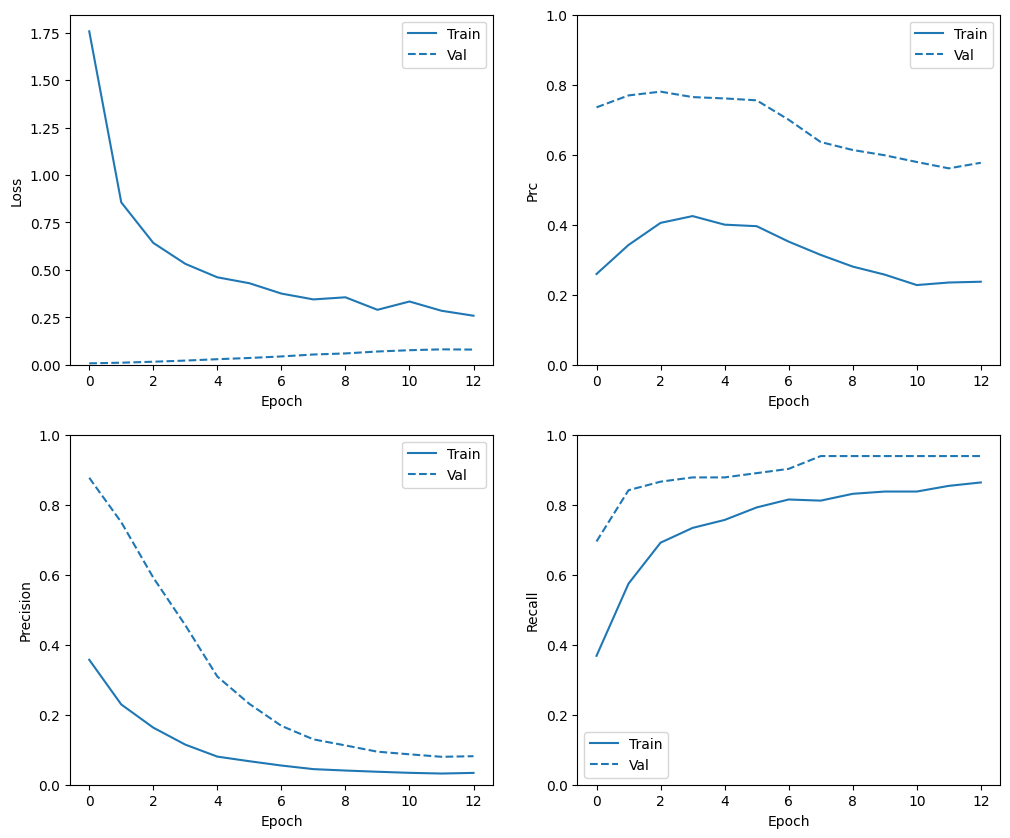
بررسی تاریخچه آموزش
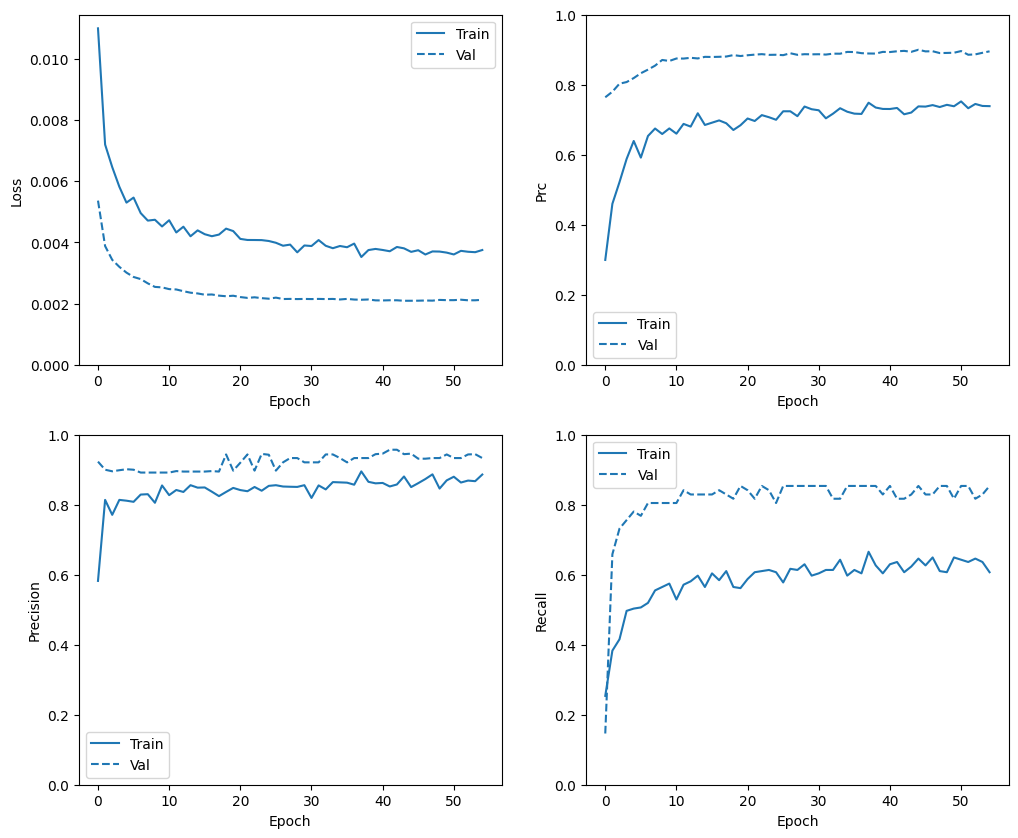
در این بخش، نمودارهایی از دقت و از دست دادن مدل خود در مجموعه آموزشی و اعتبارسنجی را تولید خواهید کرد. این موارد برای بررسی اضافه فیتینگ مفید هستند، که می توانید در آموزش Overfit و Underfit بیشتر در مورد آنها بیاموزید.
علاوه بر این، می توانید این نمودارها را برای هر یک از معیارهایی که در بالا ایجاد کردید، تولید کنید. منفی های کاذب به عنوان مثال گنجانده شده است.
def plot_metrics(history):
metrics = ['loss', 'prc', 'precision', 'recall']
for n, metric in enumerate(metrics):
name = metric.replace("_"," ").capitalize()
plt.subplot(2,2,n+1)
plt.plot(history.epoch, history.history[metric], color=colors[0], label='Train')
plt.plot(history.epoch, history.history['val_'+metric],
color=colors[0], linestyle="--", label='Val')
plt.xlabel('Epoch')
plt.ylabel(name)
if metric == 'loss':
plt.ylim([0, plt.ylim()[1]])
elif metric == 'auc':
plt.ylim([0.8,1])
else:
plt.ylim([0,1])
plt.legend();
plot_metrics(baseline_history)
معیارها را ارزیابی کنید
می توانید از یک ماتریس سردرگمی برای خلاصه کردن برچسب های واقعی در مقابل پیش بینی شده استفاده کنید، که در آن محور X برچسب پیش بینی شده و محور Y برچسب واقعی است:
train_predictions_baseline = model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_baseline = model.predict(test_features, batch_size=BATCH_SIZE)
def plot_cm(labels, predictions, p=0.5):
cm = confusion_matrix(labels, predictions > p)
plt.figure(figsize=(5,5))
sns.heatmap(cm, annot=True, fmt="d")
plt.title('Confusion matrix @{:.2f}'.format(p))
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
print('Total Fraudulent Transactions: ', np.sum(cm[1]))
مدل خود را روی مجموعه داده آزمایشی ارزیابی کنید و نتایج را برای معیارهایی که در بالا ایجاد کردید نمایش دهید:
baseline_results = model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(model.metrics_names, baseline_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_baseline)
loss : 0.0024895435199141502 tp : 59.0 fp : 7.0 tn : 56874.0 fn : 22.0 accuracy : 0.9994909167289734 precision : 0.8939393758773804 recall : 0.7283950448036194 auc : 0.9318439960479736 prc : 0.8204483985900879 Legitimate Transactions Detected (True Negatives): 56874 Legitimate Transactions Incorrectly Detected (False Positives): 7 Fraudulent Transactions Missed (False Negatives): 22 Fraudulent Transactions Detected (True Positives): 59 Total Fraudulent Transactions: 81
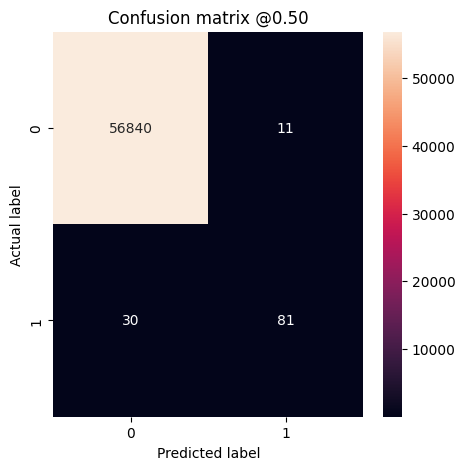
اگر مدل همه چیز را کاملاً پیشبینی کرده بود، این یک ماتریس مورب بود که مقادیر خارج از مورب اصلی، که نشاندهنده پیشبینیهای نادرست است، صفر میشد. در این مورد، ماتریس نشان میدهد که شما مثبتهای نادرست نسبتاً کمی دارید، به این معنی که تراکنشهای قانونی نسبتا کمی وجود داشته که به اشتباه پرچمگذاری شدهاند. با این حال، شما احتمالاً می خواهید با وجود هزینه افزایش تعداد موارد مثبت کاذب، منفی های کاذب کمتری داشته باشید. این مبادله ممکن است ارجح باشد زیرا منفی کاذب امکان انجام تراکنش های تقلبی را فراهم می کند، در حالی که مثبت کاذب ممکن است باعث شود ایمیلی برای مشتری ارسال شود تا از آنها بخواهد فعالیت کارت خود را تأیید کند.
ROC را ترسیم کنید
حالا ROC را رسم کنید. این نمودار مفید است زیرا در یک نگاه، محدوده عملکردی را که مدل می تواند تنها با تنظیم آستانه خروجی به آن برسد، نشان می دهد.
def plot_roc(name, labels, predictions, **kwargs):
fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)
plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
plt.xlabel('False positives [%]')
plt.ylabel('True positives [%]')
plt.xlim([-0.5,20])
plt.ylim([80,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
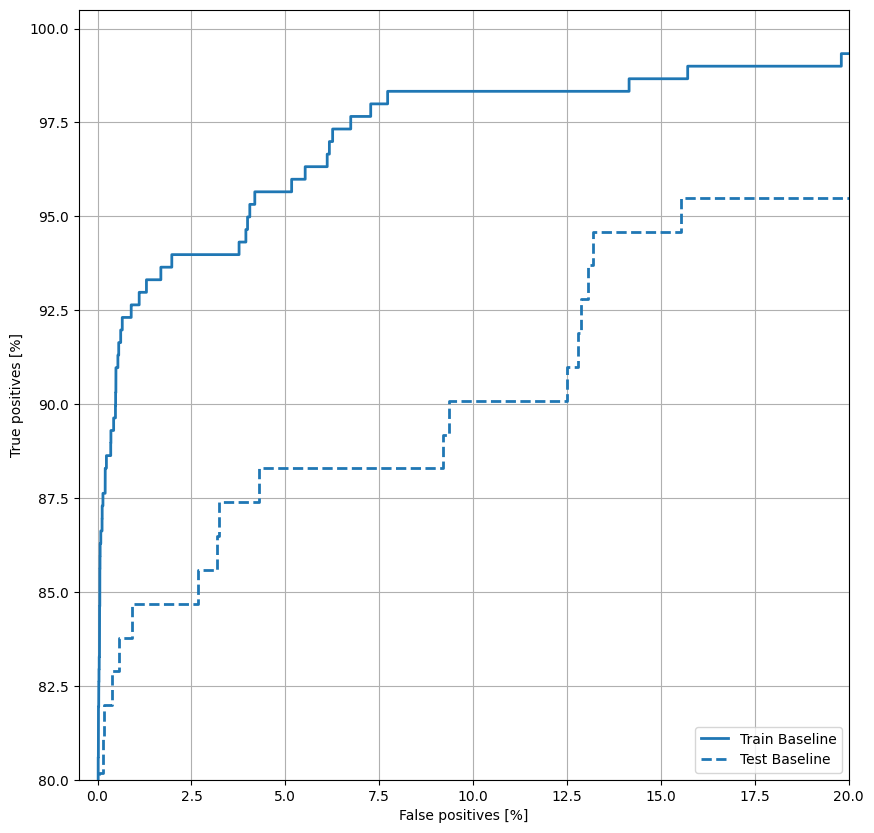
AUPRC را ترسیم کنید
اکنون AUPRC را رسم کنید. مساحت زیر منحنی دقت-یادآوری درونیابی شده، با رسم نقاط (یادآوری، دقت) برای مقادیر مختلف آستانه طبقه بندی به دست می آید. بسته به نحوه محاسبه، PR AUC ممکن است معادل دقت متوسط مدل باشد.
def plot_prc(name, labels, predictions, **kwargs):
precision, recall, _ = sklearn.metrics.precision_recall_curve(labels, predictions)
plt.plot(precision, recall, label=name, linewidth=2, **kwargs)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
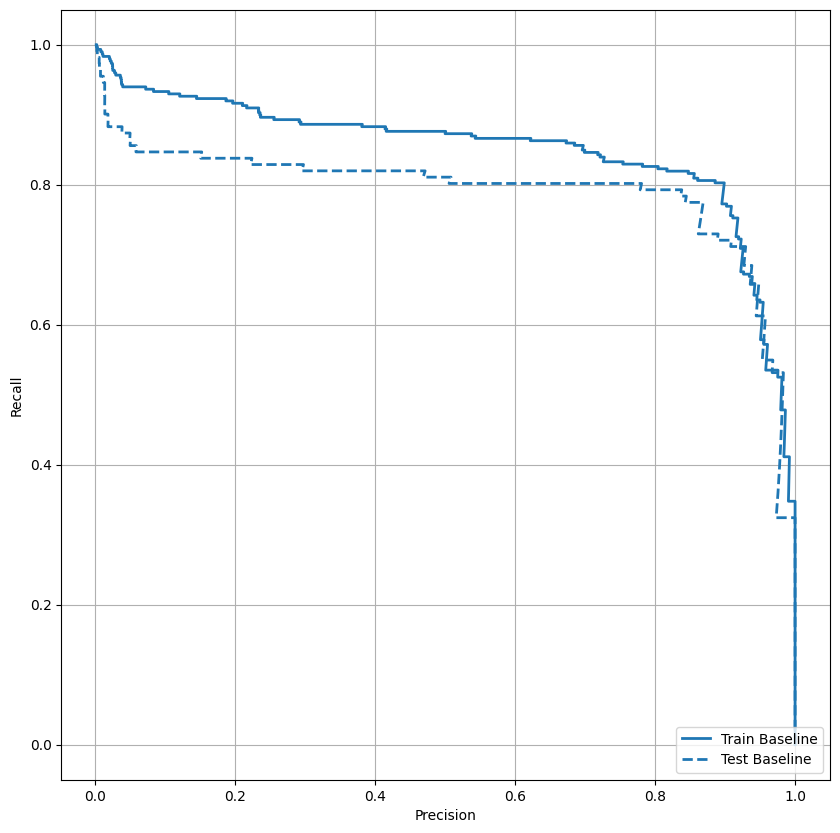
به نظر میرسد دقت نسبتاً بالاست، اما فراخوانی و ناحیه زیر منحنی ROC (AUC) آنقدر که میخواهید بالا نیست. طبقهبندیکنندهها معمولاً هنگام تلاش برای به حداکثر رساندن دقت و یادآوری با چالشهایی مواجه میشوند، که مخصوصاً هنگام کار با مجموعه دادههای نامتعادل صادق است. مهم است که هزینه انواع مختلف خطاها را در زمینه مشکلی که به آن اهمیت می دهید در نظر بگیرید. در این مثال، یک منفی کاذب (یک تراکنش متقلبانه از قلم افتاده است) ممکن است هزینه مالی داشته باشد، در حالی که مثبت کاذب (یک تراکنش به اشتباه به عنوان تقلبی پرچمگذاری شده است) ممکن است خوشحالی کاربر را کاهش دهد.
اوزان کلاس
محاسبه وزن کلاس
هدف شناسایی تراکنشهای تقلبی است، اما شما تعداد زیادی از این نمونههای مثبت را برای کار ندارید، بنابراین میخواهید که طبقهبندی کننده به مقدار زیادی از نمونههای موجود را وزن کند. شما می توانید این کار را با عبور وزن Keras برای هر کلاس از یک پارامتر انجام دهید. اینها باعث می شود که مدل به نمونه هایی از کلاسی که کمتر ارائه شده است "توجه بیشتری کند".
# Scaling by total/2 helps keep the loss to a similar magnitude.
# The sum of the weights of all examples stays the same.
weight_for_0 = (1 / neg) * (total / 2.0)
weight_for_1 = (1 / pos) * (total / 2.0)
class_weight = {0: weight_for_0, 1: weight_for_1}
print('Weight for class 0: {:.2f}'.format(weight_for_0))
print('Weight for class 1: {:.2f}'.format(weight_for_1))
Weight for class 0: 0.50 Weight for class 1: 289.44
یک مدل با وزن کلاس آموزش دهید
اکنون سعی کنید مدل را با وزن کلاس ها مجدداً آموزش دهید و ارزیابی کنید تا ببینید که چگونه بر پیش بینی ها تأثیر می گذارد.
weighted_model = make_model()
weighted_model.load_weights(initial_weights)
weighted_history = weighted_model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels),
# The class weights go here
class_weight=class_weight)
Epoch 1/100 90/90 [==============================] - 3s 15ms/step - loss: 4.1298 - tp: 59.0000 - fp: 11.0000 - tn: 238821.0000 - fn: 347.0000 - accuracy: 0.9985 - precision: 0.8429 - recall: 0.1453 - auc: 0.6238 - prc: 0.1649 - val_loss: 0.0119 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 45483.0000 - val_fn: 86.0000 - val_accuracy: 0.9981 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 - val_auc: 0.7124 - val_prc: 0.0294 Epoch 2/100 90/90 [==============================] - 1s 7ms/step - loss: 1.8711 - tp: 69.0000 - fp: 54.0000 - tn: 181897.0000 - fn: 256.0000 - accuracy: 0.9983 - precision: 0.5610 - recall: 0.2123 - auc: 0.8178 - prc: 0.2117 - val_loss: 0.0060 - val_tp: 56.0000 - val_fp: 10.0000 - val_tn: 45473.0000 - val_fn: 30.0000 - val_accuracy: 0.9991 - val_precision: 0.8485 - val_recall: 0.6512 - val_auc: 0.9427 - val_prc: 0.6870 Epoch 3/100 90/90 [==============================] - 1s 7ms/step - loss: 0.8666 - tp: 187.0000 - fp: 198.0000 - tn: 181753.0000 - fn: 138.0000 - accuracy: 0.9982 - precision: 0.4857 - recall: 0.5754 - auc: 0.9075 - prc: 0.4912 - val_loss: 0.0077 - val_tp: 65.0000 - val_fp: 19.0000 - val_tn: 45464.0000 - val_fn: 21.0000 - val_accuracy: 0.9991 - val_precision: 0.7738 - val_recall: 0.7558 - val_auc: 0.9564 - val_prc: 0.6924 Epoch 4/100 90/90 [==============================] - 1s 7ms/step - loss: 0.6876 - tp: 218.0000 - fp: 530.0000 - tn: 181421.0000 - fn: 107.0000 - accuracy: 0.9965 - precision: 0.2914 - recall: 0.6708 - auc: 0.9152 - prc: 0.5102 - val_loss: 0.0109 - val_tp: 68.0000 - val_fp: 39.0000 - val_tn: 45444.0000 - val_fn: 18.0000 - val_accuracy: 0.9987 - val_precision: 0.6355 - val_recall: 0.7907 - val_auc: 0.9661 - val_prc: 0.6926 Epoch 5/100 90/90 [==============================] - 1s 7ms/step - loss: 0.5229 - tp: 240.0000 - fp: 1102.0000 - tn: 180849.0000 - fn: 85.0000 - accuracy: 0.9935 - precision: 0.1788 - recall: 0.7385 - auc: 0.9395 - prc: 0.5228 - val_loss: 0.0154 - val_tp: 70.0000 - val_fp: 79.0000 - val_tn: 45404.0000 - val_fn: 16.0000 - val_accuracy: 0.9979 - val_precision: 0.4698 - val_recall: 0.8140 - val_auc: 0.9657 - val_prc: 0.7023 Epoch 6/100 90/90 [==============================] - 1s 7ms/step - loss: 0.4753 - tp: 251.0000 - fp: 1839.0000 - tn: 180112.0000 - fn: 74.0000 - accuracy: 0.9895 - precision: 0.1201 - recall: 0.7723 - auc: 0.9336 - prc: 0.4297 - val_loss: 0.0213 - val_tp: 70.0000 - val_fp: 156.0000 - val_tn: 45327.0000 - val_fn: 16.0000 - val_accuracy: 0.9962 - val_precision: 0.3097 - val_recall: 0.8140 - val_auc: 0.9654 - val_prc: 0.6742 Epoch 7/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3870 - tp: 270.0000 - fp: 2554.0000 - tn: 179397.0000 - fn: 55.0000 - accuracy: 0.9857 - precision: 0.0956 - recall: 0.8308 - auc: 0.9463 - prc: 0.3800 - val_loss: 0.0269 - val_tp: 70.0000 - val_fp: 264.0000 - val_tn: 45219.0000 - val_fn: 16.0000 - val_accuracy: 0.9939 - val_precision: 0.2096 - val_recall: 0.8140 - val_auc: 0.9651 - val_prc: 0.6116 Epoch 8/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3942 - tp: 268.0000 - fp: 3219.0000 - tn: 178732.0000 - fn: 57.0000 - accuracy: 0.9820 - precision: 0.0769 - recall: 0.8246 - auc: 0.9434 - prc: 0.3273 - val_loss: 0.0337 - val_tp: 70.0000 - val_fp: 355.0000 - val_tn: 45128.0000 - val_fn: 16.0000 - val_accuracy: 0.9919 - val_precision: 0.1647 - val_recall: 0.8140 - val_auc: 0.9682 - val_prc: 0.5918 Epoch 9/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3886 - tp: 271.0000 - fp: 3845.0000 - tn: 178106.0000 - fn: 54.0000 - accuracy: 0.9786 - precision: 0.0658 - recall: 0.8338 - auc: 0.9397 - prc: 0.2995 - val_loss: 0.0386 - val_tp: 70.0000 - val_fp: 406.0000 - val_tn: 45077.0000 - val_fn: 16.0000 - val_accuracy: 0.9907 - val_precision: 0.1471 - val_recall: 0.8140 - val_auc: 0.9756 - val_prc: 0.5889 Epoch 10/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2951 - tp: 281.0000 - fp: 4348.0000 - tn: 177603.0000 - fn: 44.0000 - accuracy: 0.9759 - precision: 0.0607 - recall: 0.8646 - auc: 0.9623 - prc: 0.2826 - val_loss: 0.0441 - val_tp: 72.0000 - val_fp: 464.0000 - val_tn: 45019.0000 - val_fn: 14.0000 - val_accuracy: 0.9895 - val_precision: 0.1343 - val_recall: 0.8372 - val_auc: 0.9748 - val_prc: 0.5895 Epoch 11/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2703 - tp: 280.0000 - fp: 4697.0000 - tn: 177254.0000 - fn: 45.0000 - accuracy: 0.9740 - precision: 0.0563 - recall: 0.8615 - auc: 0.9660 - prc: 0.2589 - val_loss: 0.0490 - val_tp: 72.0000 - val_fp: 552.0000 - val_tn: 44931.0000 - val_fn: 14.0000 - val_accuracy: 0.9876 - val_precision: 0.1154 - val_recall: 0.8372 - val_auc: 0.9762 - val_prc: 0.5902 Epoch 12/100 90/90 [==============================] - 1s 7ms/step - loss: 0.3358 - tp: 278.0000 - fp: 5262.0000 - tn: 176689.0000 - fn: 47.0000 - accuracy: 0.9709 - precision: 0.0502 - recall: 0.8554 - auc: 0.9468 - prc: 0.2368 - val_loss: 0.0534 - val_tp: 74.0000 - val_fp: 597.0000 - val_tn: 44886.0000 - val_fn: 12.0000 - val_accuracy: 0.9866 - val_precision: 0.1103 - val_recall: 0.8605 - val_auc: 0.9752 - val_prc: 0.5848 Epoch 13/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2833 - tp: 286.0000 - fp: 5502.0000 - tn: 176449.0000 - fn: 39.0000 - accuracy: 0.9696 - precision: 0.0494 - recall: 0.8800 - auc: 0.9582 - prc: 0.2572 - val_loss: 0.0563 - val_tp: 74.0000 - val_fp: 616.0000 - val_tn: 44867.0000 - val_fn: 12.0000 - val_accuracy: 0.9862 - val_precision: 0.1072 - val_recall: 0.8605 - val_auc: 0.9748 - val_prc: 0.5678 Epoch 14/100 90/90 [==============================] - 1s 7ms/step - loss: 0.2969 - tp: 280.0000 - fp: 5630.0000 - tn: 176321.0000 - fn: 45.0000 - accuracy: 0.9689 - precision: 0.0474 - recall: 0.8615 - auc: 0.9594 - prc: 0.2374 - val_loss: 0.0597 - val_tp: 74.0000 - val_fp: 644.0000 - val_tn: 44839.0000 - val_fn: 12.0000 - val_accuracy: 0.9856 - val_precision: 0.1031 - val_recall: 0.8605 - val_auc: 0.9741 - val_prc: 0.5627 Epoch 15/100 90/90 [==============================] - ETA: 0s - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224Restoring model weights from the end of the best epoch: 5. 90/90 [==============================] - 1s 7ms/step - loss: 0.3183 - tp: 280.0000 - fp: 5954.0000 - tn: 175997.0000 - fn: 45.0000 - accuracy: 0.9671 - precision: 0.0449 - recall: 0.8615 - auc: 0.9496 - prc: 0.2224 - val_loss: 0.0621 - val_tp: 74.0000 - val_fp: 665.0000 - val_tn: 44818.0000 - val_fn: 12.0000 - val_accuracy: 0.9851 - val_precision: 0.1001 - val_recall: 0.8605 - val_auc: 0.9771 - val_prc: 0.5550 Epoch 15: early stopping
بررسی تاریخچه آموزش
plot_metrics(weighted_history)
معیارها را ارزیابی کنید
train_predictions_weighted = weighted_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_weighted = weighted_model.predict(test_features, batch_size=BATCH_SIZE)
weighted_results = weighted_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(weighted_model.metrics_names, weighted_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_weighted)
loss : 0.014327289536595345 tp : 69.0 fp : 88.0 tn : 56793.0 fn : 12.0 accuracy : 0.9982444643974304 precision : 0.4394904375076294 recall : 0.8518518805503845 auc : 0.9410961866378784 prc : 0.7397712469100952 Legitimate Transactions Detected (True Negatives): 56793 Legitimate Transactions Incorrectly Detected (False Positives): 88 Fraudulent Transactions Missed (False Negatives): 12 Fraudulent Transactions Detected (True Positives): 69 Total Fraudulent Transactions: 81
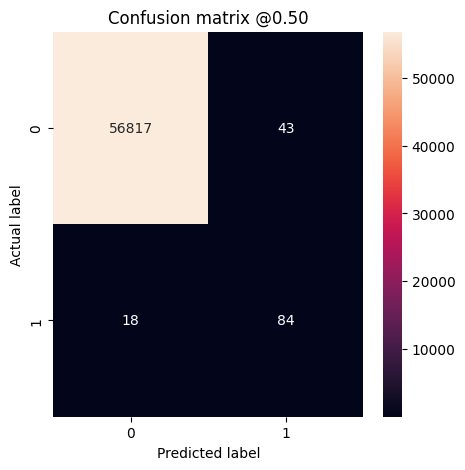
در اینجا میتوانید ببینید که با وزنهای کلاس، دقت و دقت کمتر است زیرا مثبتهای کاذب بیشتری وجود دارد، اما برعکس فراخوان و AUC بالاتر هستند زیرا مدل نیز مثبتهای واقعی بیشتری پیدا کرد. این مدل علیرغم داشتن دقت کمتر، فراخوانی بالاتری دارد (و تراکنش های تقلبی بیشتری را شناسایی می کند). البته، هر دو نوع خطا هزینهای دارد (نباید با علامتگذاری بیش از حد تراکنشهای قانونی بهعنوان تقلبی، کاربران را با مشکل مواجه کنید). به دقت مبادلات بین این انواع مختلف خطاها را برای برنامه خود در نظر بگیرید.
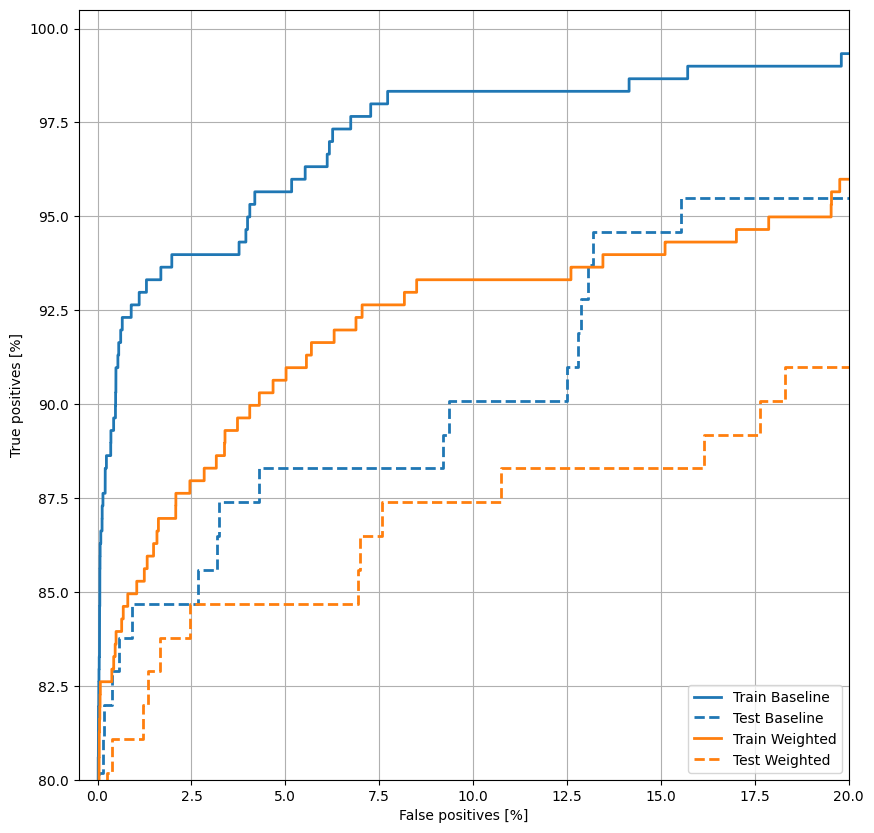
ROC را ترسیم کنید
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
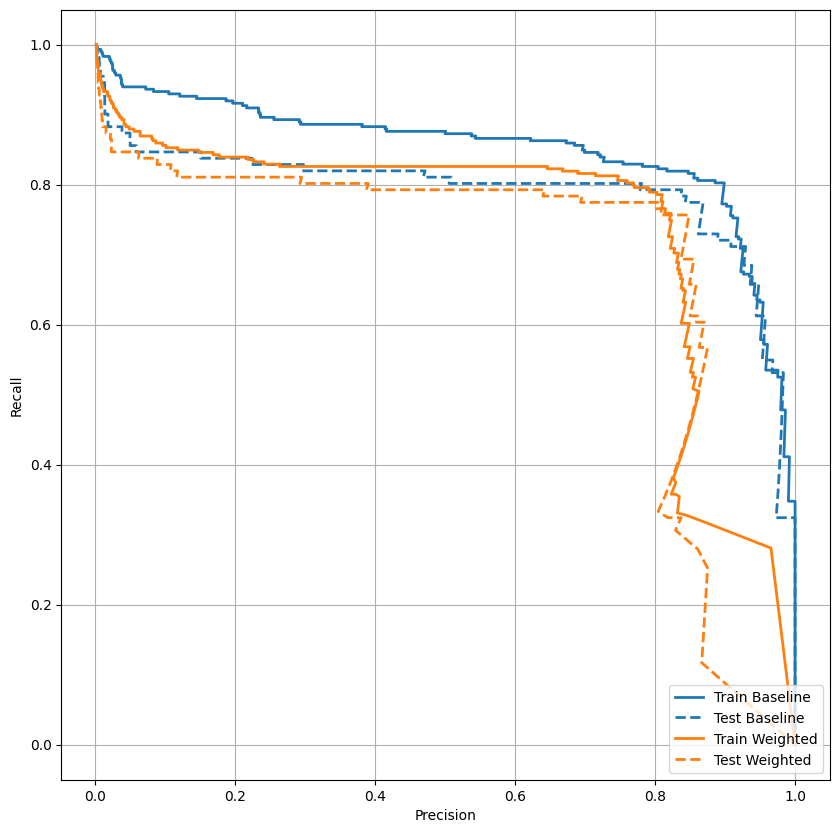
AUPRC را ترسیم کنید
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');
نمونه برداری بیش از حد
از طبقه اقلیت بیش از حد نمونه برداری کنید
یک رویکرد مرتبط، نمونهبرداری مجدد از مجموعه داده با نمونهبرداری بیش از حد از کلاس اقلیت است.
pos_features = train_features[bool_train_labels]
neg_features = train_features[~bool_train_labels]
pos_labels = train_labels[bool_train_labels]
neg_labels = train_labels[~bool_train_labels]
با استفاده از NumPy
میتوانید با انتخاب تعداد مناسب شاخصهای تصادفی از مثالهای مثبت، مجموعه داده را به صورت دستی متعادل کنید:
ids = np.arange(len(pos_features))
choices = np.random.choice(ids, len(neg_features))
res_pos_features = pos_features[choices]
res_pos_labels = pos_labels[choices]
res_pos_features.shape
(181951, 29)
resampled_features = np.concatenate([res_pos_features, neg_features], axis=0)
resampled_labels = np.concatenate([res_pos_labels, neg_labels], axis=0)
order = np.arange(len(resampled_labels))
np.random.shuffle(order)
resampled_features = resampled_features[order]
resampled_labels = resampled_labels[order]
resampled_features.shape
(363902, 29)
با استفاده از tf.data
اگر از tf.data استفاده می کنید، ساده ترین راه برای تولید نمونه های متعادل این است که با مجموعه داده های positive و negative شروع کنید و آنها را ادغام کنید. برای مثال های بیشتر به راهنمای tf.data مراجعه کنید.
BUFFER_SIZE = 100000
def make_ds(features, labels):
ds = tf.data.Dataset.from_tensor_slices((features, labels))#.cache()
ds = ds.shuffle(BUFFER_SIZE).repeat()
return ds
pos_ds = make_ds(pos_features, pos_labels)
neg_ds = make_ds(neg_features, neg_labels)
هر مجموعه داده جفت (feature, label) ارائه می دهد:
for features, label in pos_ds.take(1):
print("Features:\n", features.numpy())
print()
print("Label: ", label.numpy())
Features: [ 0.56826828 1.24841849 -2.52251105 3.84165891 0.05052604 -0.7621795 -1.43118352 0.43296139 -1.85102109 -2.50477555 3.20133397 -3.52460861 -0.95133935 -5. -1.93144512 -0.7302767 -2.46735228 0.21827555 -1.45046438 0.21081234 0.39176826 -0.23558789 -0.03611637 -0.62063738 0.3686766 0.23622961 1.2242418 0.75555829 -1.45589162] Label: 1
این دو را با استفاده از tf.data.Dataset.sample_from_datasets با هم ادغام کنید:
resampled_ds = tf.data.Dataset.sample_from_datasets([pos_ds, neg_ds], weights=[0.5, 0.5])
resampled_ds = resampled_ds.batch(BATCH_SIZE).prefetch(2)
for features, label in resampled_ds.take(1):
print(label.numpy().mean())
0.50732421875
برای استفاده از این مجموعه داده، به تعداد مراحل در هر دوره نیاز دارید.
تعریف «عصر» در این مورد کمتر روشن است. بگویید تعداد دستههایی است که برای یک بار دیدن هر نمونه منفی لازم است:
resampled_steps_per_epoch = np.ceil(2.0*neg/BATCH_SIZE)
resampled_steps_per_epoch
278.0
بر روی داده های نمونه برداری شده آموزش دهید
اکنون سعی کنید به جای استفاده از وزن کلاس، مدل را با مجموعه داده های نمونه برداری مجدد آموزش دهید تا ببینید این روش ها چگونه مقایسه می شوند.
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
val_ds = tf.data.Dataset.from_tensor_slices((val_features, val_labels)).cache()
val_ds = val_ds.batch(BATCH_SIZE).prefetch(2)
resampled_history = resampled_model.fit(
resampled_ds,
epochs=EPOCHS,
steps_per_epoch=resampled_steps_per_epoch,
callbacks=[early_stopping],
validation_data=val_ds)
Epoch 1/100 278/278 [==============================] - 10s 32ms/step - loss: 0.5508 - tp: 214194.0000 - fp: 51114.0000 - tn: 290615.0000 - fn: 70383.0000 - accuracy: 0.8060 - precision: 0.8073 - recall: 0.7527 - auc: 0.8600 - prc: 0.8879 - val_loss: 0.2279 - val_tp: 73.0000 - val_fp: 969.0000 - val_tn: 44514.0000 - val_fn: 13.0000 - val_accuracy: 0.9785 - val_precision: 0.0701 - val_recall: 0.8488 - val_auc: 0.9551 - val_prc: 0.7044 Epoch 2/100 278/278 [==============================] - 8s 28ms/step - loss: 0.2235 - tp: 253877.0000 - fp: 15743.0000 - tn: 268530.0000 - fn: 31194.0000 - accuracy: 0.9176 - precision: 0.9416 - recall: 0.8906 - auc: 0.9658 - prc: 0.9746 - val_loss: 0.1367 - val_tp: 73.0000 - val_fp: 777.0000 - val_tn: 44706.0000 - val_fn: 13.0000 - val_accuracy: 0.9827 - val_precision: 0.0859 - val_recall: 0.8488 - val_auc: 0.9596 - val_prc: 0.7072 Epoch 3/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1785 - tp: 258572.0000 - fp: 9840.0000 - tn: 274878.0000 - fn: 26054.0000 - accuracy: 0.9370 - precision: 0.9633 - recall: 0.9085 - auc: 0.9773 - prc: 0.9827 - val_loss: 0.1023 - val_tp: 72.0000 - val_fp: 699.0000 - val_tn: 44784.0000 - val_fn: 14.0000 - val_accuracy: 0.9844 - val_precision: 0.0934 - val_recall: 0.8372 - val_auc: 0.9632 - val_prc: 0.7032 Epoch 4/100 278/278 [==============================] - 8s 29ms/step - loss: 0.1571 - tp: 260447.0000 - fp: 8085.0000 - tn: 276389.0000 - fn: 24423.0000 - accuracy: 0.9429 - precision: 0.9699 - recall: 0.9143 - auc: 0.9826 - prc: 0.9863 - val_loss: 0.0869 - val_tp: 74.0000 - val_fp: 701.0000 - val_tn: 44782.0000 - val_fn: 12.0000 - val_accuracy: 0.9844 - val_precision: 0.0955 - val_recall: 0.8605 - val_auc: 0.9633 - val_prc: 0.6972 Epoch 5/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1440 - tp: 261457.0000 - fp: 7449.0000 - tn: 277093.0000 - fn: 23345.0000 - accuracy: 0.9459 - precision: 0.9723 - recall: 0.9180 - auc: 0.9855 - prc: 0.9883 - val_loss: 0.0774 - val_tp: 73.0000 - val_fp: 679.0000 - val_tn: 44804.0000 - val_fn: 13.0000 - val_accuracy: 0.9848 - val_precision: 0.0971 - val_recall: 0.8488 - val_auc: 0.9645 - val_prc: 0.6971 Epoch 6/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1349 - tp: 262460.0000 - fp: 6942.0000 - tn: 277723.0000 - fn: 22219.0000 - accuracy: 0.9488 - precision: 0.9742 - recall: 0.9220 - auc: 0.9876 - prc: 0.9896 - val_loss: 0.0718 - val_tp: 74.0000 - val_fp: 624.0000 - val_tn: 44859.0000 - val_fn: 12.0000 - val_accuracy: 0.9860 - val_precision: 0.1060 - val_recall: 0.8605 - val_auc: 0.9645 - val_prc: 0.6891 Epoch 7/100 278/278 [==============================] - 8s 28ms/step - loss: 0.1264 - tp: 263166.0000 - fp: 6780.0000 - tn: 278253.0000 - fn: 21145.0000 - accuracy: 0.9510 - precision: 0.9749 - recall: 0.9256 - auc: 0.9895 - prc: 0.9909 - val_loss: 0.0672 - val_tp: 75.0000 - val_fp: 602.0000 - val_tn: 44881.0000 - val_fn: 11.0000 - val_accuracy: 0.9865 - val_precision: 0.1108 - val_recall: 0.8721 - val_auc: 0.9670 - val_prc: 0.6822 Epoch 8/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1190 - tp: 264216.0000 - fp: 6569.0000 - tn: 278270.0000 - fn: 20289.0000 - accuracy: 0.9528 - precision: 0.9757 - recall: 0.9287 - auc: 0.9910 - prc: 0.9920 - val_loss: 0.0628 - val_tp: 74.0000 - val_fp: 570.0000 - val_tn: 44913.0000 - val_fn: 12.0000 - val_accuracy: 0.9872 - val_precision: 0.1149 - val_recall: 0.8605 - val_auc: 0.9671 - val_prc: 0.6830 Epoch 9/100 278/278 [==============================] - 9s 31ms/step - loss: 0.1125 - tp: 264562.0000 - fp: 6339.0000 - tn: 279137.0000 - fn: 19306.0000 - accuracy: 0.9550 - precision: 0.9766 - recall: 0.9320 - auc: 0.9924 - prc: 0.9930 - val_loss: 0.0576 - val_tp: 74.0000 - val_fp: 544.0000 - val_tn: 44939.0000 - val_fn: 12.0000 - val_accuracy: 0.9878 - val_precision: 0.1197 - val_recall: 0.8605 - val_auc: 0.9672 - val_prc: 0.6828 Epoch 10/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1064 - tp: 266549.0000 - fp: 6112.0000 - tn: 278323.0000 - fn: 18360.0000 - accuracy: 0.9570 - precision: 0.9776 - recall: 0.9356 - auc: 0.9934 - prc: 0.9937 - val_loss: 0.0544 - val_tp: 74.0000 - val_fp: 541.0000 - val_tn: 44942.0000 - val_fn: 12.0000 - val_accuracy: 0.9879 - val_precision: 0.1203 - val_recall: 0.8605 - val_auc: 0.9638 - val_prc: 0.6827 Epoch 11/100 278/278 [==============================] - 8s 30ms/step - loss: 0.1005 - tp: 267048.0000 - fp: 6123.0000 - tn: 278896.0000 - fn: 17277.0000 - accuracy: 0.9589 - precision: 0.9776 - recall: 0.9392 - auc: 0.9943 - prc: 0.9944 - val_loss: 0.0493 - val_tp: 74.0000 - val_fp: 500.0000 - val_tn: 44983.0000 - val_fn: 12.0000 - val_accuracy: 0.9888 - val_precision: 0.1289 - val_recall: 0.8605 - val_auc: 0.9578 - val_prc: 0.6761 Epoch 12/100 277/278 [============================>.] - ETA: 0s - loss: 0.0950 - tp: 266855.0000 - fp: 6079.0000 - tn: 277677.0000 - fn: 16685.0000 - accuracy: 0.9599 - precision: 0.9777 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949Restoring model weights from the end of the best epoch: 2. 278/278 [==============================] - 8s 29ms/step - loss: 0.0950 - tp: 267815.0000 - fp: 6094.0000 - tn: 278693.0000 - fn: 16742.0000 - accuracy: 0.9599 - precision: 0.9778 - recall: 0.9412 - auc: 0.9950 - prc: 0.9949 - val_loss: 0.0451 - val_tp: 74.0000 - val_fp: 468.0000 - val_tn: 45015.0000 - val_fn: 12.0000 - val_accuracy: 0.9895 - val_precision: 0.1365 - val_recall: 0.8605 - val_auc: 0.9581 - val_prc: 0.6683 Epoch 12: early stopping
اگر فرآیند آموزش کل مجموعه داده را در هر به روز رسانی گرادیان در نظر می گرفت، این نمونه برداری بیش از حد اساساً با وزن کلاس یکسان بود.
اما هنگام آموزش مدل به صورت دستهای، همانطور که در اینجا انجام دادید، دادههای بیش از نمونهگیری شده سیگنال گرادیان نرمتری ارائه میدهند: به جای اینکه هر مثال مثبت در یک دسته با وزن زیاد نشان داده شود، هر بار در دستههای مختلف با یک نشان داده میشود. وزن کم
این سیگنال گرادیان نرم تر، آموزش مدل را آسان تر می کند.
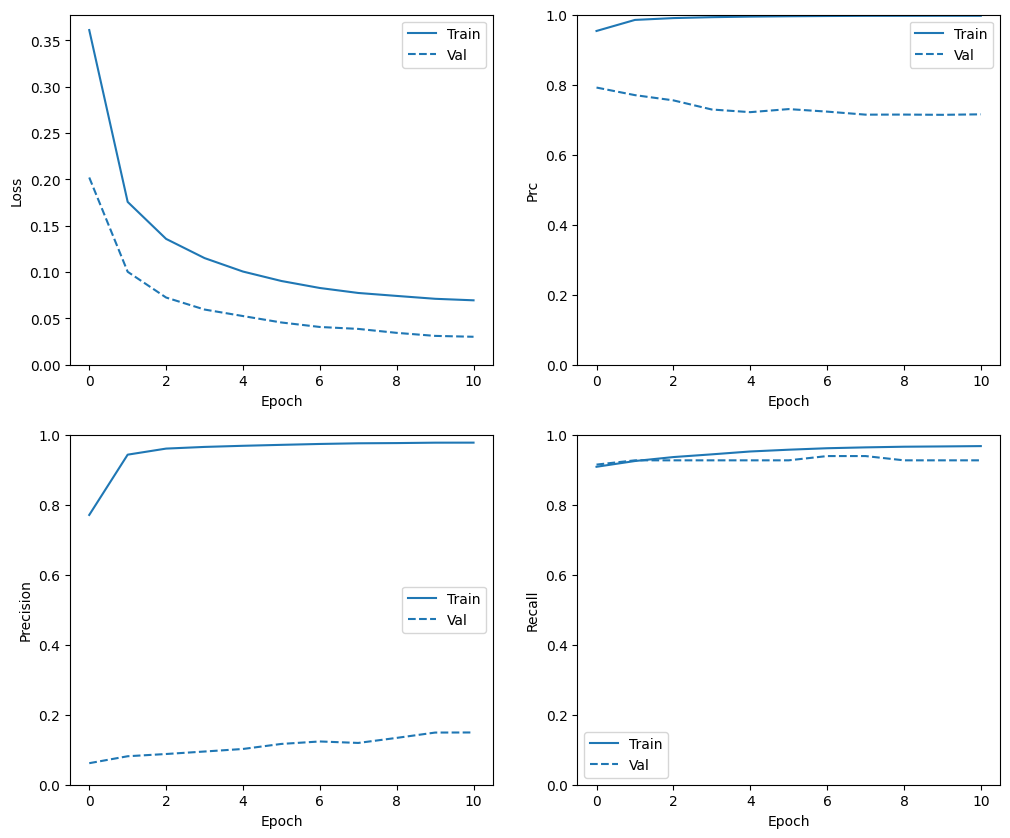
بررسی تاریخچه آموزش
توجه داشته باشید که توزیع معیارها در اینجا متفاوت خواهد بود، زیرا داده های آموزشی توزیع کاملاً متفاوتی با داده های اعتبار سنجی و آزمایش دارند.
plot_metrics(resampled_history)
دوباره آموزش دهید
از آنجایی که آموزش با داده های متعادل آسان تر است، روش آموزشی فوق ممکن است به سرعت بیش از حد انجام شود.
بنابراین دورهها را جدا کنید تا به tf.keras.callbacks.EarlyStopping کنترل دقیقتری بر روی زمان توقف تمرین بدهید.
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
resampled_history = resampled_model.fit(
resampled_ds,
# These are not real epochs
steps_per_epoch=20,
epochs=10*EPOCHS,
callbacks=[early_stopping],
validation_data=(val_ds))
Epoch 1/1000 20/20 [==============================] - 3s 73ms/step - loss: 2.0114 - tp: 3382.0000 - fp: 5181.0000 - tn: 60589.0000 - fn: 17377.0000 - accuracy: 0.7393 - precision: 0.3950 - recall: 0.1629 - auc: 0.6308 - prc: 0.3325 - val_loss: 0.4343 - val_tp: 7.0000 - val_fp: 5042.0000 - val_tn: 40441.0000 - val_fn: 79.0000 - val_accuracy: 0.8876 - val_precision: 0.0014 - val_recall: 0.0814 - val_auc: 0.2282 - val_prc: 0.0012 Epoch 2/1000 20/20 [==============================] - 1s 33ms/step - loss: 1.2163 - tp: 7466.0000 - fp: 5137.0000 - tn: 15257.0000 - fn: 13100.0000 - accuracy: 0.5548 - precision: 0.5924 - recall: 0.3630 - auc: 0.4763 - prc: 0.5716 - val_loss: 0.4539 - val_tp: 36.0000 - val_fp: 5893.0000 - val_tn: 39590.0000 - val_fn: 50.0000 - val_accuracy: 0.8696 - val_precision: 0.0061 - val_recall: 0.4186 - val_auc: 0.6494 - val_prc: 0.0054 Epoch 3/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.7406 - tp: 12289.0000 - fp: 5509.0000 - tn: 14872.0000 - fn: 8290.0000 - accuracy: 0.6631 - precision: 0.6905 - recall: 0.5972 - auc: 0.6803 - prc: 0.7580 - val_loss: 0.4611 - val_tp: 75.0000 - val_fp: 6273.0000 - val_tn: 39210.0000 - val_fn: 11.0000 - val_accuracy: 0.8621 - val_precision: 0.0118 - val_recall: 0.8721 - val_auc: 0.9293 - val_prc: 0.4539 Epoch 4/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.5071 - tp: 15891.0000 - fp: 5370.0000 - tn: 15013.0000 - fn: 4686.0000 - accuracy: 0.7545 - precision: 0.7474 - recall: 0.7723 - auc: 0.8298 - prc: 0.8757 - val_loss: 0.4451 - val_tp: 78.0000 - val_fp: 5505.0000 - val_tn: 39978.0000 - val_fn: 8.0000 - val_accuracy: 0.8790 - val_precision: 0.0140 - val_recall: 0.9070 - val_auc: 0.9443 - val_prc: 0.6777 Epoch 5/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.4284 - tp: 17046.0000 - fp: 5072.0000 - tn: 15496.0000 - fn: 3346.0000 - accuracy: 0.7945 - precision: 0.7707 - recall: 0.8359 - auc: 0.8827 - prc: 0.9151 - val_loss: 0.4140 - val_tp: 77.0000 - val_fp: 4338.0000 - val_tn: 41145.0000 - val_fn: 9.0000 - val_accuracy: 0.9046 - val_precision: 0.0174 - val_recall: 0.8953 - val_auc: 0.9463 - val_prc: 0.6903 Epoch 6/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.3836 - tp: 17606.0000 - fp: 4362.0000 - tn: 16113.0000 - fn: 2879.0000 - accuracy: 0.8232 - precision: 0.8014 - recall: 0.8595 - auc: 0.9080 - prc: 0.9336 - val_loss: 0.3824 - val_tp: 77.0000 - val_fp: 3314.0000 - val_tn: 42169.0000 - val_fn: 9.0000 - val_accuracy: 0.9271 - val_precision: 0.0227 - val_recall: 0.8953 - val_auc: 0.9475 - val_prc: 0.6752 Epoch 7/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3574 - tp: 17856.0000 - fp: 3894.0000 - tn: 16553.0000 - fn: 2657.0000 - accuracy: 0.8401 - precision: 0.8210 - recall: 0.8705 - auc: 0.9208 - prc: 0.9432 - val_loss: 0.3538 - val_tp: 76.0000 - val_fp: 2592.0000 - val_tn: 42891.0000 - val_fn: 10.0000 - val_accuracy: 0.9429 - val_precision: 0.0285 - val_recall: 0.8837 - val_auc: 0.9486 - val_prc: 0.6819 Epoch 8/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3377 - tp: 17766.0000 - fp: 3483.0000 - tn: 17067.0000 - fn: 2644.0000 - accuracy: 0.8504 - precision: 0.8361 - recall: 0.8705 - auc: 0.9280 - prc: 0.9481 - val_loss: 0.3271 - val_tp: 76.0000 - val_fp: 2047.0000 - val_tn: 43436.0000 - val_fn: 10.0000 - val_accuracy: 0.9549 - val_precision: 0.0358 - val_recall: 0.8837 - val_auc: 0.9497 - val_prc: 0.6910 Epoch 9/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.3188 - tp: 17749.0000 - fp: 2855.0000 - tn: 17547.0000 - fn: 2809.0000 - accuracy: 0.8617 - precision: 0.8614 - recall: 0.8634 - auc: 0.9360 - prc: 0.9539 - val_loss: 0.3051 - val_tp: 74.0000 - val_fp: 1657.0000 - val_tn: 43826.0000 - val_fn: 12.0000 - val_accuracy: 0.9634 - val_precision: 0.0427 - val_recall: 0.8605 - val_auc: 0.9514 - val_prc: 0.7022 Epoch 10/1000 20/20 [==============================] - 1s 33ms/step - loss: 0.3046 - tp: 17772.0000 - fp: 2599.0000 - tn: 17841.0000 - fn: 2748.0000 - accuracy: 0.8695 - precision: 0.8724 - recall: 0.8661 - auc: 0.9402 - prc: 0.9570 - val_loss: 0.2860 - val_tp: 74.0000 - val_fp: 1398.0000 - val_tn: 44085.0000 - val_fn: 12.0000 - val_accuracy: 0.9691 - val_precision: 0.0503 - val_recall: 0.8605 - val_auc: 0.9527 - val_prc: 0.6997 Epoch 11/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2937 - tp: 17673.0000 - fp: 2352.0000 - tn: 18273.0000 - fn: 2662.0000 - accuracy: 0.8776 - precision: 0.8825 - recall: 0.8691 - auc: 0.9447 - prc: 0.9595 - val_loss: 0.2687 - val_tp: 73.0000 - val_fp: 1235.0000 - val_tn: 44248.0000 - val_fn: 13.0000 - val_accuracy: 0.9726 - val_precision: 0.0558 - val_recall: 0.8488 - val_auc: 0.9534 - val_prc: 0.7066 Epoch 12/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2813 - tp: 17721.0000 - fp: 2109.0000 - tn: 18523.0000 - fn: 2607.0000 - accuracy: 0.8849 - precision: 0.8936 - recall: 0.8718 - auc: 0.9485 - prc: 0.9621 - val_loss: 0.2524 - val_tp: 73.0000 - val_fp: 1098.0000 - val_tn: 44385.0000 - val_fn: 13.0000 - val_accuracy: 0.9756 - val_precision: 0.0623 - val_recall: 0.8488 - val_auc: 0.9539 - val_prc: 0.7094 Epoch 13/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2706 - tp: 18031.0000 - fp: 1869.0000 - tn: 18502.0000 - fn: 2558.0000 - accuracy: 0.8919 - precision: 0.9061 - recall: 0.8758 - auc: 0.9520 - prc: 0.9652 - val_loss: 0.2395 - val_tp: 73.0000 - val_fp: 1037.0000 - val_tn: 44446.0000 - val_fn: 13.0000 - val_accuracy: 0.9770 - val_precision: 0.0658 - val_recall: 0.8488 - val_auc: 0.9549 - val_prc: 0.7119 Epoch 14/1000 20/20 [==============================] - 1s 37ms/step - loss: 0.2665 - tp: 18087.0000 - fp: 1748.0000 - tn: 18567.0000 - fn: 2558.0000 - accuracy: 0.8949 - precision: 0.9119 - recall: 0.8761 - auc: 0.9525 - prc: 0.9661 - val_loss: 0.2283 - val_tp: 73.0000 - val_fp: 972.0000 - val_tn: 44511.0000 - val_fn: 13.0000 - val_accuracy: 0.9784 - val_precision: 0.0699 - val_recall: 0.8488 - val_auc: 0.9556 - val_prc: 0.7045 Epoch 15/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2589 - tp: 18064.0000 - fp: 1630.0000 - tn: 18830.0000 - fn: 2436.0000 - accuracy: 0.9007 - precision: 0.9172 - recall: 0.8812 - auc: 0.9560 - prc: 0.9676 - val_loss: 0.2180 - val_tp: 73.0000 - val_fp: 941.0000 - val_tn: 44542.0000 - val_fn: 13.0000 - val_accuracy: 0.9791 - val_precision: 0.0720 - val_recall: 0.8488 - val_auc: 0.9563 - val_prc: 0.7069 Epoch 16/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2495 - tp: 18132.0000 - fp: 1481.0000 - tn: 18926.0000 - fn: 2421.0000 - accuracy: 0.9047 - precision: 0.9245 - recall: 0.8822 - auc: 0.9587 - prc: 0.9695 - val_loss: 0.2079 - val_tp: 73.0000 - val_fp: 905.0000 - val_tn: 44578.0000 - val_fn: 13.0000 - val_accuracy: 0.9799 - val_precision: 0.0746 - val_recall: 0.8488 - val_auc: 0.9565 - val_prc: 0.7110 Epoch 17/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2435 - tp: 18047.0000 - fp: 1378.0000 - tn: 19144.0000 - fn: 2391.0000 - accuracy: 0.9080 - precision: 0.9291 - recall: 0.8830 - auc: 0.9601 - prc: 0.9706 - val_loss: 0.1990 - val_tp: 73.0000 - val_fp: 882.0000 - val_tn: 44601.0000 - val_fn: 13.0000 - val_accuracy: 0.9804 - val_precision: 0.0764 - val_recall: 0.8488 - val_auc: 0.9568 - val_prc: 0.7118 Epoch 18/1000 20/20 [==============================] - 1s 37ms/step - loss: 0.2396 - tp: 18223.0000 - fp: 1289.0000 - tn: 19075.0000 - fn: 2373.0000 - accuracy: 0.9106 - precision: 0.9339 - recall: 0.8848 - auc: 0.9612 - prc: 0.9714 - val_loss: 0.1911 - val_tp: 73.0000 - val_fp: 870.0000 - val_tn: 44613.0000 - val_fn: 13.0000 - val_accuracy: 0.9806 - val_precision: 0.0774 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7148 Epoch 19/1000 20/20 [==============================] - 1s 36ms/step - loss: 0.2324 - tp: 18179.0000 - fp: 1205.0000 - tn: 19254.0000 - fn: 2322.0000 - accuracy: 0.9139 - precision: 0.9378 - recall: 0.8867 - auc: 0.9633 - prc: 0.9728 - val_loss: 0.1839 - val_tp: 73.0000 - val_fp: 857.0000 - val_tn: 44626.0000 - val_fn: 13.0000 - val_accuracy: 0.9809 - val_precision: 0.0785 - val_recall: 0.8488 - val_auc: 0.9576 - val_prc: 0.7165 Epoch 20/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2318 - tp: 18119.0000 - fp: 1224.0000 - tn: 19279.0000 - fn: 2338.0000 - accuracy: 0.9130 - precision: 0.9367 - recall: 0.8857 - auc: 0.9640 - prc: 0.9728 - val_loss: 0.1758 - val_tp: 73.0000 - val_fp: 823.0000 - val_tn: 44660.0000 - val_fn: 13.0000 - val_accuracy: 0.9817 - val_precision: 0.0815 - val_recall: 0.8488 - val_auc: 0.9573 - val_prc: 0.7185 Epoch 21/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2233 - tp: 18041.0000 - fp: 1074.0000 - tn: 19514.0000 - fn: 2331.0000 - accuracy: 0.9169 - precision: 0.9438 - recall: 0.8856 - auc: 0.9660 - prc: 0.9745 - val_loss: 0.1690 - val_tp: 73.0000 - val_fp: 813.0000 - val_tn: 44670.0000 - val_fn: 13.0000 - val_accuracy: 0.9819 - val_precision: 0.0824 - val_recall: 0.8488 - val_auc: 0.9578 - val_prc: 0.7211 Epoch 22/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2193 - tp: 18258.0000 - fp: 1013.0000 - tn: 19414.0000 - fn: 2275.0000 - accuracy: 0.9197 - precision: 0.9474 - recall: 0.8892 - auc: 0.9666 - prc: 0.9753 - val_loss: 0.1634 - val_tp: 73.0000 - val_fp: 817.0000 - val_tn: 44666.0000 - val_fn: 13.0000 - val_accuracy: 0.9818 - val_precision: 0.0820 - val_recall: 0.8488 - val_auc: 0.9580 - val_prc: 0.7123 Epoch 23/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2114 - tp: 18439.0000 - fp: 993.0000 - tn: 19417.0000 - fn: 2111.0000 - accuracy: 0.9242 - precision: 0.9489 - recall: 0.8973 - auc: 0.9696 - prc: 0.9774 - val_loss: 0.1577 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9584 - val_prc: 0.7122 Epoch 24/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2076 - tp: 18459.0000 - fp: 896.0000 - tn: 19582.0000 - fn: 2023.0000 - accuracy: 0.9287 - precision: 0.9537 - recall: 0.9012 - auc: 0.9694 - prc: 0.9776 - val_loss: 0.1528 - val_tp: 73.0000 - val_fp: 807.0000 - val_tn: 44676.0000 - val_fn: 13.0000 - val_accuracy: 0.9820 - val_precision: 0.0830 - val_recall: 0.8488 - val_auc: 0.9587 - val_prc: 0.7129 Epoch 25/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.2044 - tp: 18340.0000 - fp: 907.0000 - tn: 19664.0000 - fn: 2049.0000 - accuracy: 0.9278 - precision: 0.9529 - recall: 0.8995 - auc: 0.9707 - prc: 0.9783 - val_loss: 0.1483 - val_tp: 73.0000 - val_fp: 800.0000 - val_tn: 44683.0000 - val_fn: 13.0000 - val_accuracy: 0.9822 - val_precision: 0.0836 - val_recall: 0.8488 - val_auc: 0.9591 - val_prc: 0.7054 Epoch 26/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1997 - tp: 18293.0000 - fp: 918.0000 - tn: 19749.0000 - fn: 2000.0000 - accuracy: 0.9288 - precision: 0.9522 - recall: 0.9014 - auc: 0.9722 - prc: 0.9788 - val_loss: 0.1433 - val_tp: 73.0000 - val_fp: 788.0000 - val_tn: 44695.0000 - val_fn: 13.0000 - val_accuracy: 0.9824 - val_precision: 0.0848 - val_recall: 0.8488 - val_auc: 0.9590 - val_prc: 0.7059 Epoch 27/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1987 - tp: 18562.0000 - fp: 848.0000 - tn: 19530.0000 - fn: 2020.0000 - accuracy: 0.9300 - precision: 0.9563 - recall: 0.9019 - auc: 0.9720 - prc: 0.9791 - val_loss: 0.1394 - val_tp: 73.0000 - val_fp: 784.0000 - val_tn: 44699.0000 - val_fn: 13.0000 - val_accuracy: 0.9825 - val_precision: 0.0852 - val_recall: 0.8488 - val_auc: 0.9595 - val_prc: 0.7062 Epoch 28/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.1944 - tp: 18320.0000 - fp: 828.0000 - tn: 19823.0000 - fn: 1989.0000 - accuracy: 0.9312 - precision: 0.9568 - recall: 0.9021 - auc: 0.9734 - prc: 0.9798 - val_loss: 0.1351 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9598 - val_prc: 0.7079 Epoch 29/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.1933 - tp: 18455.0000 - fp: 827.0000 - tn: 19704.0000 - fn: 1974.0000 - accuracy: 0.9316 - precision: 0.9571 - recall: 0.9034 - auc: 0.9732 - prc: 0.9797 - val_loss: 0.1313 - val_tp: 73.0000 - val_fp: 766.0000 - val_tn: 44717.0000 - val_fn: 13.0000 - val_accuracy: 0.9829 - val_precision: 0.0870 - val_recall: 0.8488 - val_auc: 0.9599 - val_prc: 0.7094 Epoch 30/1000 20/20 [==============================] - 1s 35ms/step - loss: 0.1910 - tp: 18417.0000 - fp: 768.0000 - tn: 19858.0000 - fn: 1917.0000 - accuracy: 0.9344 - precision: 0.9600 - recall: 0.9057 - auc: 0.9740 - prc: 0.9802 - val_loss: 0.1282 - val_tp: 73.0000 - val_fp: 759.0000 - val_tn: 44724.0000 - val_fn: 13.0000 - val_accuracy: 0.9831 - val_precision: 0.0877 - val_recall: 0.8488 - val_auc: 0.9602 - val_prc: 0.7094 Epoch 31/1000 20/20 [==============================] - ETA: 0s - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811Restoring model weights from the end of the best epoch: 21. 20/20 [==============================] - 1s 34ms/step - loss: 0.1866 - tp: 18494.0000 - fp: 756.0000 - tn: 19815.0000 - fn: 1895.0000 - accuracy: 0.9353 - precision: 0.9607 - recall: 0.9071 - auc: 0.9753 - prc: 0.9811 - val_loss: 0.1246 - val_tp: 73.0000 - val_fp: 742.0000 - val_tn: 44741.0000 - val_fn: 13.0000 - val_accuracy: 0.9834 - val_precision: 0.0896 - val_recall: 0.8488 - val_auc: 0.9597 - val_prc: 0.7095 Epoch 31: early stopping
تاریخچه آموزش را دوباره بررسی کنید
plot_metrics(resampled_history)
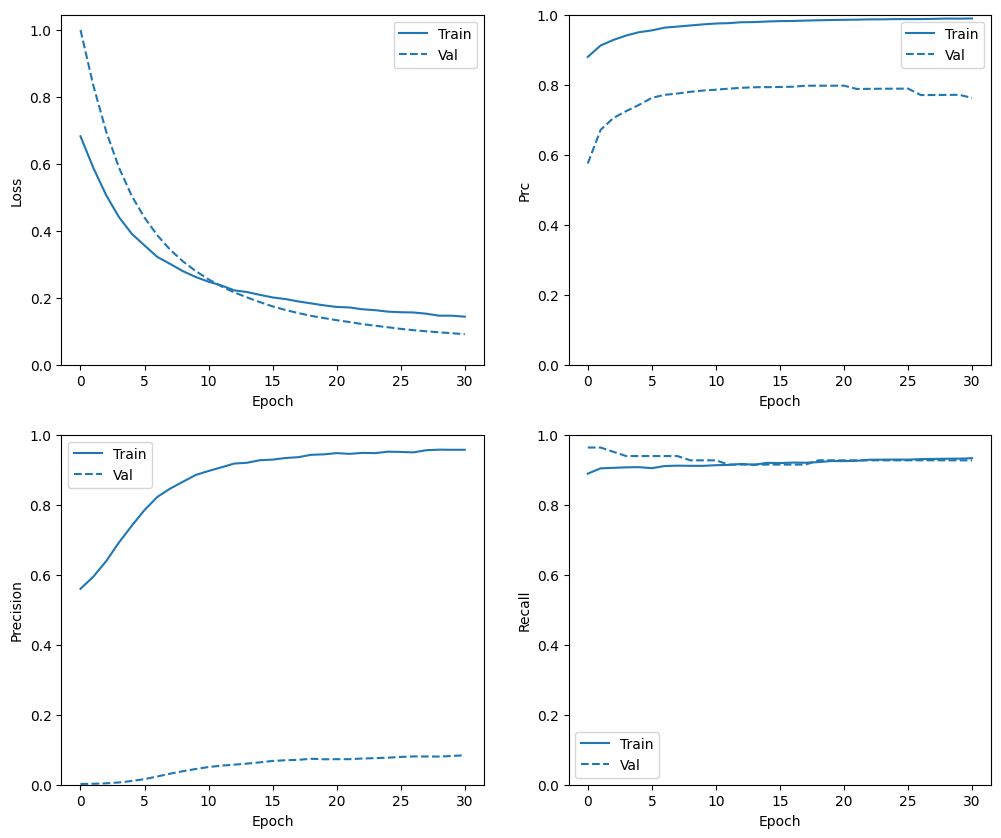
معیارها را ارزیابی کنید
train_predictions_resampled = resampled_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_resampled = resampled_model.predict(test_features, batch_size=BATCH_SIZE)
resampled_results = resampled_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(resampled_model.metrics_names, resampled_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_resampled)
loss : 0.16882120072841644 tp : 71.0 fp : 1032.0 tn : 55849.0 fn : 10.0 accuracy : 0.9817070960998535 precision : 0.06436990201473236 recall : 0.8765432238578796 auc : 0.9518552422523499 prc : 0.7423797845840454 Legitimate Transactions Detected (True Negatives): 55849 Legitimate Transactions Incorrectly Detected (False Positives): 1032 Fraudulent Transactions Missed (False Negatives): 10 Fraudulent Transactions Detected (True Positives): 71 Total Fraudulent Transactions: 81
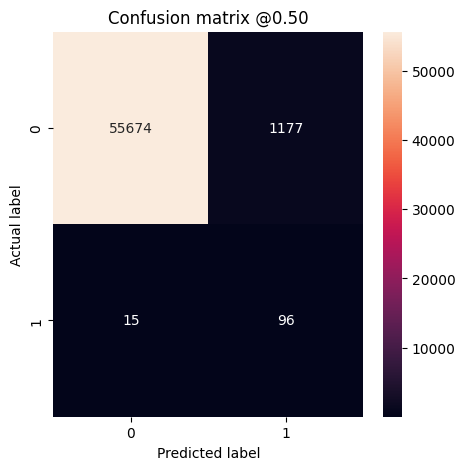
ROC را ترسیم کنید
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_roc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_roc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
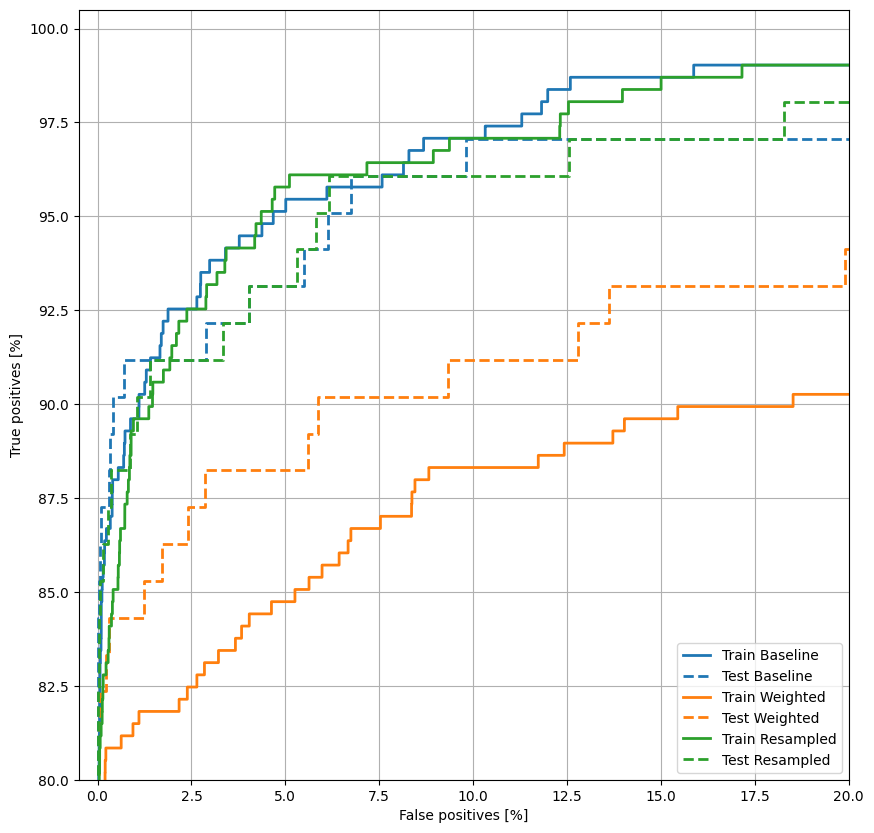
AUPRC را ترسیم کنید
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_prc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_prc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
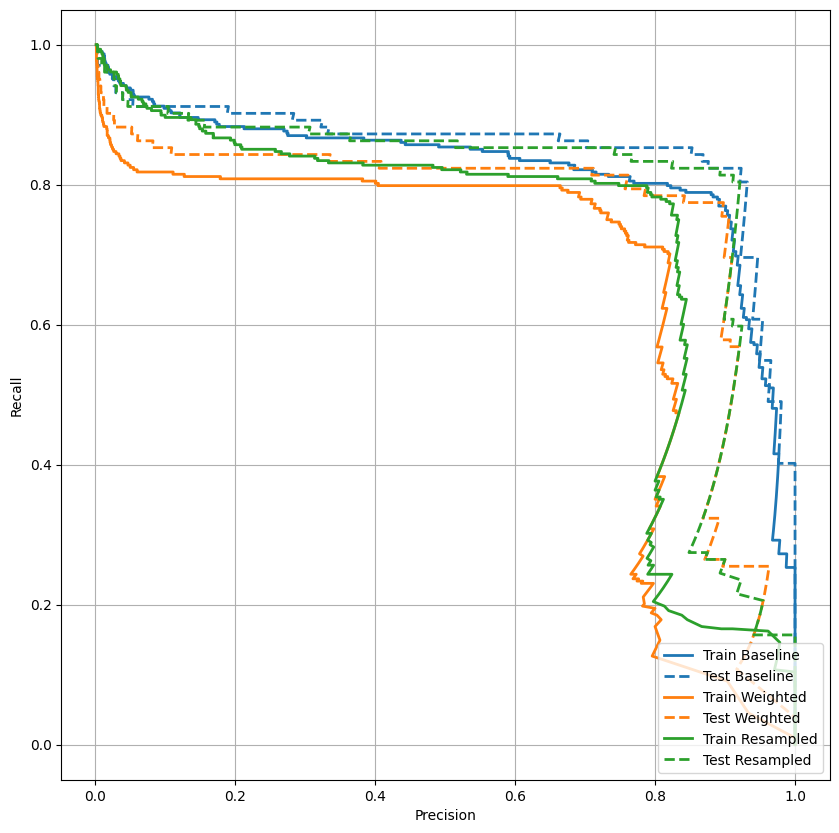
استفاده از این آموزش برای مشکل شما
طبقه بندی نامتعادل داده ها یک کار ذاتا دشوار است زیرا نمونه های کمی برای یادگیری وجود دارد. همیشه باید ابتدا با داده ها شروع کنید و تمام تلاش خود را برای جمع آوری نمونه های بیشتری انجام دهید و در مورد ویژگی هایی که ممکن است مرتبط باشند فکر کنید تا مدل بتواند بیشترین استفاده را از طبقه اقلیت شما داشته باشد. در برخی مواقع مدل شما ممکن است برای بهبود و به دست آوردن نتایجی که می خواهید دچار مشکل شود، بنابراین مهم است که زمینه مشکل خود و معاوضه بین انواع مختلف خطاها را در نظر داشته باشید.
